paradoja de gibbs

Experimento mental en física estadística.

En mecánica estadística , una derivación semiclásica de la entropía que no tiene en cuenta la indistinguibilidad de las partículas produce una expresión de entropía que no es extensiva (no es proporcional a la cantidad de sustancia en cuestión). Esto conduce a una paradoja conocida como la paradoja de Gibbs , en honor a Josiah Willard Gibbs , quien propuso este experimento mental en 1874-1875. ^{[1] [2]} La paradoja permite que la entropía de los sistemas cerrados disminuya, violando la segunda ley de la termodinámica . Una paradoja relacionada es la "paradoja de la mezcla". Si se adopta la perspectiva de que la definición de entropía debe cambiarse para ignorar la permutación de partículas, en el límite termodinámico , se evita la paradoja.

Ilustración del problema

Gibbs consideró la siguiente dificultad que surge si la entropía del gas ideal no es extensa. ^[1] Dos contenedores de un gas ideal se encuentran uno al lado del otro. El gas del recipiente n.° 1 es idéntico en todos los aspectos al gas del recipiente n.° 2 (es decir, en volumen, masa, temperatura, presión, etc.). En consecuencia, tienen la misma entropía S. Ahora se abre una puerta en la pared del contenedor para permitir que las partículas de gas se mezclen entre los contenedores. No se producen cambios macroscópicos, ya que el sistema está en equilibrio. Pero si la fórmula de la entropía no es extensa, la entropía del sistema combinado no será 2 S . De hecho, la cantidad particular de entropía no extensiva considerada por Gibbs predice entropía adicional (más de 2 S ). Cerrar la puerta reduce nuevamente la entropía a S por caja, en aparente violación de la Segunda Ley de la Termodinámica .

Como lo entendió Gibbs, ^[2] y lo volvió a enfatizar más recientemente, ^{[3] [4],} esto es un mal uso de la cantidad de entropía no extensiva de Gibbs. Si las partículas de gas son distinguibles, cerrar las puertas no devolverá el sistema a su estado original: muchas de las partículas habrán cambiado de contenedor. Existe libertad para definir qué está "ordenado" y sería un error concluir que la entropía no ha aumentado. En particular, la cantidad de entropía no extensiva de Gibbs para un gas ideal no está destinada a situaciones en las que cambia el número de partículas.

La paradoja se evita asumiendo la indistinguibilidad (al menos la indistinguibilidad efectiva) de las partículas en el volumen. Esto da como resultado la extensa ecuación de Sackur-Tetrode para la entropía, como se deriva a continuación.

Calcular la entropía del gas ideal y hacerlo extensivo.

En la mecánica clásica, el estado de un gas ideal de energía U , volumen V y con N partículas, cada partícula con masa m , se representa especificando el vector de momento p y el vector de posición x para cada partícula. Se puede considerar que esto especifica un punto en un espacio de fases de 6 dimensiones N , donde cada uno de los ejes corresponde a una de las coordenadas de momento o posición de una de las partículas. El conjunto de puntos en el espacio de fases que podría ocupar el gas está especificado por la restricción de que el gas tendrá una energía particular:

${\displaystyle U={\frac {1}{2m}}\sum _{i=1}^{N}(p_{ix}^{2}+p_{iy}^{2}+p_{iz}^{2})}$

y estar contenido dentro del volumen V (digamos que V es un cubo de lado X de modo que V = X ³ ):

${\displaystyle 0\leq x_{ij}\leq X}$

Para y ${\displaystyle i=1...N}$ ${\displaystyle j=1,2,3}$

La primera restricción define la superficie de una hiperesfera tridimensional de radio (2 mU ) ^1/2 y la segunda es un hipercubo tridimensional de volumen V ^N. Estos se combinan para formar un hipercilindro de 6 dimensiones N. Así como el área de la pared de un cilindro es la circunferencia de la base multiplicada por la altura, el área φ de la pared de este hipercilindro es:

${\displaystyle \phi (U,V,N)=V^{N}\left({\frac {2\pi ^{\frac {3N}{2}}(2mU)^{\frac {3N-1}{2}}}{\Gamma (3N/2)}}\right)~~~~~~~~~~~(1)}$

La entropía es proporcional al logaritmo del número de estados que podría tener el gas cumpliendo estas restricciones. En la física clásica, el número de estados es infinitamente grande, pero según la mecánica cuántica es finito. Antes del advenimiento de la mecánica cuántica, este infinito se regularizaba haciendo que el espacio de fases fuera discreto. El espacio de fases se dividió en bloques de volumen h ^{3 N} . La constante h apareció así como resultado de un truco matemático y se pensó que no tenía significado físico. Sin embargo, utilizando la mecánica cuántica se recupera el mismo formalismo en el límite semiclásico, pero ahora siendo h la constante de Planck. Esto se puede ver cualitativamente a partir del principio de incertidumbre de Heisenberg ; no se puede especificar un volumen en el espacio de fase N menor que h ^{3 N} ( h es la constante de Planck).

Para calcular el número de estados debemos calcular el volumen en el espacio de fase en el que se puede encontrar el sistema y dividirlo por h ^{3 N.} Esto nos lleva a otro problema: el volumen parece acercarse a cero, ya que la región del espacio de fases en la que puede estar el sistema es un área de espesor cero. Este problema es producto de haber especificado la energía U con precisión infinita. En un sistema genérico sin simetrías, un tratamiento cuántico completo produciría un conjunto discreto no degenerado de estados propios de energía. Una especificación exacta de la energía fijaría entonces el estado preciso en el que se encuentra el sistema, por lo que el número de estados disponibles para el sistema sería uno y, por tanto, la entropía sería cero.

Cuando especificamos que la energía interna es U , lo que realmente queremos decir es que la energía total del gas se encuentra en algún lugar de un intervalo de longitud alrededor de U. Aquí se toma como muy pequeño, resulta que la entropía no depende en gran medida de la elección de para N grande . Esto significa que el "área" anterior φ debe extenderse a una capa de un espesor igual a una incertidumbre en el momento , por lo que la entropía viene dada por: ${\displaystyle \delta U}$ ${\displaystyle \delta U}$ ${\displaystyle \delta U}$ ${\displaystyle \delta p=\delta \left({\sqrt {2mU}}\right)={\sqrt {\frac {m}{2U}}}\delta U}$

${\displaystyle \left.\right.S=k\,\ln(\phi \delta p/h^{3N})}$

donde la constante de proporcionalidad es k , la constante de Boltzmann . Usando la aproximación de Stirling para la función Gamma que omite términos de orden menor que N , la entropía para N grande se convierte en:

${\displaystyle S=kN\ln \left[V\left({\frac {U}{N}}\right)^{\frac {3}{2}}\right]+{\frac {3}{2}}kN\left(1+\ln {\frac {4\pi m}{3h^{2}}}\right)}$

Esta cantidad no es extensiva como se puede ver al considerar dos volúmenes idénticos con el mismo número de partículas y la misma energía. Supongamos que los dos volúmenes están separados por una barrera al principio. Quitar o reinsertar la pared es reversible, pero la entropía aumenta cuando la barrera se elimina en la cantidad

${\displaystyle \delta S=k\left[2N\ln(2V)-N\ln V-N\ln V\right]=2kN\ln 2>0}$

lo cual está en contradicción con la termodinámica si se vuelve a insertar la barrera. Ésta es la paradoja de Gibbs.

La paradoja se resuelve postulando que las partículas de gas son, de hecho, indistinguibles. Esto significa que todos los estados que difieren sólo por una permutación de partículas deben considerarse como el mismo estado. Por ejemplo, si tenemos un gas de 2 partículas y especificamos AB como un estado del gas donde la primera partícula ( A ) tiene momento p ₁ y la segunda partícula ( B ) tiene momento p ₂ , entonces este estado así como el estado BA donde la partícula B tiene momento p ₁ y la partícula A tiene momento p ₂ debe contarse como el mismo estado.

Para un gas de N -partículas, hay N ! estados que son idénticos en este sentido, si se supone que cada partícula se encuentra en un estado de partícula única diferente. Se puede hacer esta suposición con seguridad siempre que el gas no tenga una densidad extremadamente alta. En condiciones normales, se puede calcular así el volumen del espacio de fase ocupado por el gas, dividiendo la Ecuación 1 por N !. Usando nuevamente la aproximación de Stirling para N grande , ln( N !) ≈ N ln( N ) − N , la entropía para N grande es:

${\displaystyle S=kN\ln \left[\left({\frac {V}{N}}\right)\left({\frac {U}{N}}\right)^{\frac {3}{2}}\right]+kN\left({\frac {5}{2}}+{\frac {3}{2}}\ln {\frac {4\pi m}{3h^{2}}}\right)}$

que puede demostrarse fácilmente que es extenso. Esta es la ecuación de Sackur-Tetrode .

La paradoja de la mezcla

Una paradoja estrechamente relacionada con la paradoja de Gibbs es la paradoja de la mezcla . La paradoja de Gibbs es un caso especial de la "paradoja de la mezcla" que contiene todas las características destacadas. La diferencia es que la paradoja de la mezcla trata de distinciones arbitrarias en los dos gases, no sólo de distinciones en el orden de las partículas como había considerado Gibbs. En este sentido, se trata de una generalización sencilla del argumento expuesto por Gibbs. Nuevamente tome una caja con una partición, con el gas A en un lado y el gas B en el otro, y ambos gases están a la misma temperatura y presión. Si los gases A y B son gases diferentes, surge una entropía una vez que los gases se mezclan. Si los gases son iguales, no se calcula ninguna entropía adicional. La entropía adicional resultante de la mezcla no depende del carácter de los gases; sólo depende del hecho de que los gases sean diferentes. Los dos gases pueden ser arbitrariamente similares, pero la entropía resultante de la mezcla no desaparece a menos que sean el mismo gas: una discontinuidad paradójica.

Esta "paradoja" puede explicarse considerando cuidadosamente la definición de entropía. En particular, como explica de manera concisa Edwin Thompson Jaynes , ^[2] las definiciones de entropía son arbitrarias.

Como señala un ejemplo central en el artículo de Jaynes, se puede desarrollar una teoría que trate dos gases como similares incluso si esos gases pueden en realidad distinguirse mediante mediciones suficientemente detalladas. Mientras no realicemos estas mediciones detalladas, la teoría no tendrá inconsistencias internas. (En otras palabras, no importa que llamemos a los gases A y B con el mismo nombre si aún no hemos descubierto que son distintos.) Si nuestra teoría llama iguales a los gases A y B, entonces la entropía no cambia cuando mézclalos. Si nuestra teoría considera que los gases A y B son diferentes, entonces la entropía aumenta cuando se mezclan. Esta idea sugiere que las ideas de "estado termodinámico" y de "entropía" son algo subjetivas.

El aumento diferencial de entropía ( dS ) como resultado de mezclar gases diferentes, multiplicado por la temperatura ( T ), equivale a la cantidad mínima de trabajo que debemos hacer para restaurar los gases a su estado original separado. Supongamos que dos gases son diferentes, pero que no podemos detectar sus diferencias. Si estos gases están en una caja, separados unos de otros por una partición, ¿cuánto trabajo se necesita para restaurar el estado original del sistema después de quitar la partición y dejar que los gases se mezclen?

Ninguno: simplemente reinserte la partición. Aunque los gases se mezclaron, nunca hubo un cambio de estado detectable en el sistema porque, según la hipótesis, los gases son experimentalmente indistinguibles.

Tan pronto como podemos distinguir la diferencia entre gases, el trabajo necesario para recuperar la configuración macroscópica previa a la mezcla desde el estado posterior a la mezcla se vuelve distinto de cero. Esta cantidad de trabajo no depende de cuán diferentes sean los gases, sino sólo de si son distinguibles.

Esta línea de razonamiento es particularmente informativa cuando se consideran los conceptos de partículas indistinguibles y el conteo correcto de Boltzmann . La expresión original de Boltzmann para el número de estados disponibles para un gas suponía que un estado podría expresarse en términos de un número de "subniveles" de energía, cada uno de los cuales contiene un número particular de partículas. Mientras que las partículas de un subnivel determinado se consideraban indistinguibles entre sí, las partículas de diferentes subniveles se consideraban distinguibles de las partículas de cualquier otro subnivel. Esto equivale a decir que el intercambio de dos partículas en dos subniveles diferentes dará como resultado un "macroestado de intercambio" del gas detectablemente diferente. Por ejemplo, si consideramos un gas simple con N partículas, con una densidad suficientemente baja como para que sea prácticamente seguro que cada subnivel contenga una partícula o ninguna (es decir, un gas Maxwell-Boltzmann), esto significa que un simple contenedor de gas será en uno de N ! "macroestados de intercambio" detectablemente diferentes, uno para cada posible intercambio de partículas.

Así como la paradoja de la mezcla comienza con dos contenedores detectablemente diferentes, y la entropía adicional que resulta de la mezcla es proporcional a la cantidad promedio de trabajo necesario para restaurar ese estado inicial después de la mezcla, así la entropía adicional en la derivación original de Boltzmann es proporcional al promedio cantidad de trabajo requerida para restaurar el gas simple desde algún "macroestado de intercambio" a su "macroestado de intercambio" original. Si suponemos que, de hecho, no existe ninguna diferencia detectable experimentalmente en estos "macroestados de intercambio" disponibles, entonces utilizar la entropía que resulta de suponer que las partículas son indistinguibles producirá una teoría consistente. Este es el "conteo correcto de Boltzmann".

A menudo se dice que la resolución de la paradoja de Gibbs deriva del hecho de que, según la teoría cuántica, las partículas similares son en principio indistinguibles. Según el razonamiento de Jaynes, si las partículas son experimentalmente indistinguibles por cualquier razón, la paradoja de Gibbs se resuelve, y la mecánica cuántica sólo proporciona una seguridad de que en el reino cuántico, esta indistinguibilidad será cierta como una cuestión de principio, en lugar de deberse a una capacidad experimental insuficientemente refinada.

Entropía no extensiva de dos gases ideales y cómo solucionarla

En esta sección, presentamos a grandes rasgos una derivación puramente clásica de la entropía no extensiva para un gas ideal considerada por Gibbs antes de tener en cuenta el "recuento correcto" (indistinguibilidad de partículas). A esto le sigue una breve discusión de dos métodos estándar para hacer extensiva la entropía. Finalmente, presentamos un tercer método, debido a R. Swendsen, para obtener un resultado extenso (aditivo) para la entropía de dos sistemas si se les permite intercambiar partículas entre sí. ^{[5] [6]}

Configuración

Presentaremos una versión simplificada del cálculo. Se diferencia del cálculo completo en tres aspectos:

1. El gas ideal está formado por partículas confinadas a una dimensión espacial.
2. Mantenemos solo los términos de orden , eliminando todos los términos de tamaño n o menos, donde n es el número de partículas. Para nuestros propósitos, esto es suficiente, porque aquí es donde aparece la paradoja de Gibbs y donde debe resolverse. Los términos desatendidos desempeñan un papel cuando el número de partículas no es muy grande, como en la simulación por computadora y la nanotecnología . Además, son necesarios para derivar la ecuación de Sackur-Tetrode . ${\displaystyle n\log(n)}$
3. Se omite la subdivisión del espacio de fases en unidades de la constante de Planck ( h ). En cambio, la entropía se define utilizando una integral sobre la porción "accesible" del espacio de fase. Esto sirve para resaltar el carácter puramente clásico del cálculo.

Comenzamos con una versión de la entropía de Boltzmann en la que el integrando es todo el espacio de fase accesible :

${\displaystyle S=k\ln \Omega =k\ln \oint \limits _{H({\vec {p}},{\vec {q}})=E}(d{\vec {p}}\,)^{n}(d{\vec {q}}\,)^{n}}$

La integral está restringida a un contorno de regiones disponibles del espacio de fase, sujeto a la conservación de energía. A diferencia de las integrales de línea unidimensionales que se encuentran en la física elemental, el contorno de energía constante posee un gran número de dimensiones. La justificación para integrar en el espacio de fases utilizando la medida canónica implica el supuesto de igual probabilidad. La suposición se puede hacer invocando la hipótesis ergódica así como el teorema de Liouville de los sistemas hamiltonianos .

(La hipótesis ergódica subyace a la capacidad de un sistema físico para alcanzar el equilibrio térmico , pero es posible que esto no siempre sea válido para simulaciones por computadora (ver el problema de Fermi-Pasta-Ulam-Tsingou ) o en ciertos sistemas del mundo real, como los plasmas no térmicos. .)

El teorema de Liouville supone un número fijo de dimensiones que el sistema "explora". En los cálculos de entropía, el número de dimensiones es proporcional al número de partículas en el sistema, lo que obliga al espacio de fases a cambiar abruptamente de dimensionalidad cuando se suman o restan partículas. Esto puede explicar las dificultades para construir una derivación clara y simple de la dependencia de la entropía del número de partículas.

Para el gas ideal, el espacio de fases accesible es una ( n − 1 ) -esfera (también llamada hiperesfera) en el n -espacio dimensional : ${\displaystyle {\vec {v}}}$

${\displaystyle E=\sum _{j=1}^{n}{\frac {1}{2}}mv_{j}^{2}\,,}$

Para recuperar el resultado paradójico de que la entropía no es extensiva, integramos el espacio de fases de un gas de partículas monoatómicas confinadas a una única dimensión espacial mediante . Dado que nuestro único propósito es iluminar una paradoja, simplificamos la notación tomando la masa de la partícula y la constante de Boltzmann igual a la unidad: . Representamos puntos en el espacio de fases y sus partes x y v mediante vectores de n y 2 n dimensiones: ${\displaystyle n}$ ${\displaystyle 0<x<\ell }$ ${\displaystyle m=k=1}$

${\displaystyle {\vec {\xi }}=[x_{1},...,x_{n},v_{1},...,v_{n}]=[{\vec {x}},{\vec {v}}\,]}$   dónde     y   ${\displaystyle {\vec {x}}=[x_{1},...,x_{n}]}$ ${\displaystyle {\vec {v}}=[v_{1},...,v_{n}]\,.}$

Para calcular la entropía, utilizamos el hecho de que la esfera (n-1) tiene un "volumen de hipersuperficie" ( n − 1) dimensional de ${\displaystyle \Sigma v_{j}^{2}=R^{2}\,,}$

${\displaystyle {\tilde {A}}_{n}(R)={\frac {n\pi ^{n/2}}{(n/2)!}}R^{n-1}\,.}$

Por ejemplo, si n = 2, la 1-esfera es el círculo , una "hipersuperficie" en el plano. Cuando la esfera es de dimensión par ( n impar), será necesario utilizar la función gamma para darle significado al factorial; vea abajo. ${\displaystyle {\tilde {A}}_{2}(R)=2\pi R}$

Paradoja de Gibbs en un gas unidimensional

La paradoja de Gibbs surge cuando la entropía se calcula utilizando un espacio de fase dimensional, donde también está el número de partículas en el gas. Estas partículas están confinadas espacialmente al intervalo unidimensional . El volumen de la superficie de energía fija es ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle \ell ^{n}}$

${\displaystyle \Omega _{E,\ell }=\left(\int dx_{1}\int dx_{2}...\int dx_{n}\right)\left(\underbrace {\int dv_{1}\int dv_{2}...\int dv_{n}} _{\Sigma v_{i}^{2}=2E}\right)}$

Los subíndices de se utilizan para definir las 'variables de estado' y se analizarán más adelante, cuando se argumente que el número de partículas carece de estatus completo como variable de estado en este cálculo. La integral sobre el espacio de configuración es . Como lo indica el soporte inferior, la integral sobre el espacio de velocidades está restringida al "área de superficie" de la hiperesfera n - 1 dimensional de radio y, por lo tanto, es igual al "área" de esa hipersuperficie. De este modo ${\displaystyle \Omega }$ ${\displaystyle n}$ ${\displaystyle \ell ^{n}}$ ${\displaystyle {\sqrt {2E}}}$

${\displaystyle \Omega _{E,\ell }=\ell ^{n}{\frac {n\pi ^{n/2}}{(n/2)!}}(2E)^{\frac {n-1}{2}}}$

Después de aproximar el factorial y eliminar los términos pequeños, obtenemos

${\displaystyle {\begin{aligned}\ln \Omega _{E,\ell }&\approx n\ln \ell +n\ln {\sqrt {\frac {E}{n}}}+{\text{const.}}\\&=\underbrace {n\ln {\frac {\ell }{n}}+n\ln {\sqrt {\frac {E}{n}}}} _{\text{extensive}}+\,n\ln n+{\text{const.}}\\\end{aligned}}}$

En la segunda expresión, el término fue restado y sumado, utilizando el hecho de que . Esto se hizo para resaltar exactamente cómo la "entropía" definida aquí no llega a ser una propiedad extensiva de la materia. Los dos primeros términos son extensos: si el volumen del sistema se duplica, pero se llena con la misma densidad de partículas con la misma energía, entonces cada uno de estos términos se duplica. Pero el tercer término no es ni extenso ni intensivo y, por tanto, es erróneo. ${\displaystyle n\ln n}$ ${\displaystyle \ln \ell -\ln n=\ln(\ell /n)}$

Se ha agregado la constante arbitraria porque generalmente se puede considerar que la entropía está definida hasta una constante aditiva arbitraria. Esto es especialmente necesario cuando la entropía se define como el logaritmo de un volumen del espacio de fase medido en unidades de posición-momento. Cualquier cambio en la forma en que se definen estas unidades sumará o restará una constante del valor de la entropía.

Dos formas estándar de hacer extensiva la entropía clásica

Como se analizó anteriormente, se recupera una forma extensa de entropía si dividimos el volumen del espacio de fase, por n !. Un enfoque alternativo es argumentar que no se puede confiar en la dependencia del número de partículas basándose en que el cambio también cambia la dimensionalidad del espacio de fases. Tales cambios de dimensionalidad quedan fuera del alcance de la mecánica hamiltoniana y del teorema de Liouville . Por esa razón es plausible permitir que la constante arbitraria sea función de . ^[7] Definiendo la función como, tenemos: ${\displaystyle \Omega _{E,\ell }}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle f(n)=-{\frac {3}{2}}n\ln n}$

${\displaystyle {\begin{aligned}S=\ln \Omega _{E,\ell }&\approx n\ln \ell +n\ln {\sqrt {E}}+{\text{const.}}\\&=n\ln \ell +n\ln {\sqrt {E}}+f(n)\\\ln \Omega _{E,\ell ,n}&\approx n\ln {\frac {\ell }{n}}+n\ln {\sqrt {\frac {E}{n}}}+{\text{const.}},\\\end{aligned}}}$

que tiene una amplia escala:

${\displaystyle S(\alpha E,\alpha \ell ,\alpha n)=\alpha \,S(E,\ell ,n)}$

El enfoque de intercambio de partículas de Swendsen

Siguiendo a Swendsen, ^{[5] [6]} permitimos que dos sistemas intercambien partículas. Básicamente, esto "hace espacio" en el espacio de fases para que las partículas entren o salgan sin requerir un cambio en el número de dimensiones del espacio de fases. El número total de partículas es : ${\displaystyle N}$

• ${\displaystyle n_{A}}$las partículas tienen coordenadas . ${\displaystyle 0<x<\ell _{A}}$

  La energía total de estas partículas es ${\displaystyle E_{A}}$

• ${\displaystyle n_{B}}$las partículas tienen coordenadas . ${\displaystyle 0<x<\ell _{B}}$

  La energía total de estas partículas es ${\displaystyle E_{B}}$

• El sistema está sujeto a las restricciones y ${\displaystyle E_{A}+E_{B}=E}$ ${\displaystyle n_{A}+n_{B}=N}$

Tomando la integral sobre el espacio de fases, tenemos:

${\displaystyle {\begin{aligned}\Omega _{E,\ell ,N}&=\left(\underbrace {\int dx_{?}...\int dx_{?}} _{n_{A}\;{\text{terms}}}\underbrace {\int dx_{?}...\int dx_{N}} _{n_{B}\;{\text{terms}}}\right)\left(\underbrace {\int dv_{1}\int dv_{2}...\int dv_{N}} _{\Sigma v^{2}=2E_{A}\;{\text{or}}\;\Sigma v^{2}=2E_{B}}\right)\\&=\left(\ell _{A}\right)^{n_{A}}\left(\ell _{B}\right)^{n_{B}}\left(\underbrace {\frac {N!}{n_{A}!n_{B}!}} _{\text{combination}}\right)\left(\underbrace {{\frac {n_{A}\pi ^{n_{A}/2}}{(n_{A}/2)!}}(2E_{A})^{\frac {n_{A}-1}{2}}} _{n_{A}-{\text{sphere}}}\right)\left(\underbrace {{\frac {n_{B}\pi ^{n_{B}/2}}{(n_{B}/2)!}}(2E_{B})^{\frac {n_{B}-1}{2}}} _{n_{B}-{\text{sphere}}}\right)\end{aligned}}}$

Los signos de interrogación (?) sirven como recordatorio de que no podemos suponer que las primeras n _A partículas (es decir, 1 a n _A ) están en el sistema A mientras que las otras partículas ( n _B a N ) están en el sistema B. (Esto se analiza con más detalle en la siguiente sección).

Tomando el logaritmo y manteniendo sólo los términos mayores, tenemos:

$${\displaystyle S=\ln \Omega _{E,\ell ,N}\approx n_{A}\ln \left({\frac {n_{A}}{\ell _{A}}}{\sqrt {\frac {E_{A}}{\ell _{A}}}}\right)+n_{B}\ln \left({\frac {n_{B}}{\ell _{B}}}{\sqrt {\frac {E_{B}}{\ell _{B}}}}\right)+N\ln N+{\text{const.}}}$$

Esto puede interpretarse como la suma de la entropía del sistema A y del sistema B , ambos extensivos. Y hay un término que no es extenso. ${\displaystyle N\ln N}$

Visualizando el enfoque del intercambio de partículas en tres dimensiones

Un gas ideal de tres partículas dividido en dos partes.

Se obtuvieron las fórmulas correctas (extensivas) para los sistemas A y B porque incluimos todas las formas posibles en que los dos sistemas podrían intercambiar partículas. El uso de combinaciones (es decir, N partículas eligen N _A ) se utilizó para determinar el número de formas en que N partículas se pueden dividir en el sistema A que contiene n partículas _A y el sistema B que contiene n partículas _B. Este recuento no se justifica por motivos físicos, sino por la necesidad de integrar el espacio de fases. Como se ilustrará a continuación, el espacio de fases no contiene una sola n _A -esfera y una sola n _B -esfera, sino que en su lugar

${\displaystyle {N \choose n_{A}}={\frac {N!}{n_{A}!n_{B}!}}}$

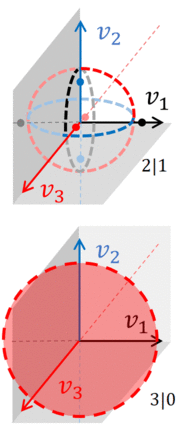
pares de n -esferas, todas situadas en el mismo ( N + 1) -espacio de velocidad dimensional. La integral sobre el espacio de fase accesible debe incluir todas estas n -esferas, como se puede ver en la figura, que muestra la velocidad real del espacio de fase asociada con un gas que consta de tres partículas. Además, este gas se ha dividido en dos sistemas , A y B.

Si ignoramos las variables espaciales, el espacio de fases de un gas con tres partículas es tridimensional, lo que permite esbozar las n -esferas sobre las cuales se debe tomar la integral sobre el espacio de fases. Si las tres partículas están juntas, la división entre los dos gases es 3|0. El espacio de fase accesible está delimitado por una esfera ordinaria ( 2-esfera ) con un radio que es o (dependiendo de qué sistema tenga las partículas). ${\displaystyle {\sqrt {2E_{1}}}}$ ${\displaystyle {\sqrt {2E_{2}}}}$

Si la división es 2|1, entonces el espacio de fases consta de círculos y puntos . Cada círculo ocupa dos dimensiones y, para cada círculo, dos puntos se encuentran en el tercer eje, equidistantes del centro del círculo. En otras palabras, si el sistema A tiene 2 partículas, el espacio de fase accesible consta de 3 pares de n -esferas , siendo cada par una esfera 1 y una esfera 0 :

${\displaystyle v_{1}^{2}+v_{2}^{2}=2E_{A}\qquad v_{3}^{2}=2E_{B}}$

${\displaystyle v_{2}^{2}+v_{3}^{2}=2E_{A}\qquad v_{1}^{2}=2E_{B}}$

${\displaystyle v_{3}^{2}+v_{1}^{2}=2E_{A}\qquad v_{2}^{2}=2E_{B}}$

Tenga en cuenta que

${\displaystyle {3 \choose 2}=3.}$

Referencias

1. Gibbs, J. Willard (1875–1878). Sobre el equilibrio de sustancias heterogéneas . Académico de Connecticut. Ciencia. ISBN 0-8493-9685-9.Reimpreso en Gibbs, J. Willard (octubre de 1993). Los artículos científicos de J. Willard Gibbs (Vol. 1) . Prensa de arco de buey. ISBN 0-918024-77-3. y en Gibbs, J. Willard (febrero de 1994). Los artículos científicos de J. Willard Gibbs (Vol. 2) . Prensa de arco de buey. ISBN 1-881987-06-X.
2. Jaynes, Edwin T (1996). "La paradoja de Gibbs" (PDF) . Consultado el 8 de noviembre de 2005 .
3. Graduado, Harold (1961). "Las muchas caras de la entropía". Comunicaciones sobre Matemática Pura y Aplicada . 14 (3): 323–354. doi :10.1002/cpa.3160140312.
4. van Kampen, NG (1984). "La paradoja de Gibbs". En WE Parry (ed.). Ensayos de física teórica en honor a Dirk ter Haar . Oxford: Pérgamo. ISBN 978-0080265230.
5. Swendsen, Robert (marzo de 2006). "Mecánica estadística de coloides y definición de entropía de Boltzmann". Revista Estadounidense de Física . 74 (3): 187-190. Código Bib : 2006AmJPh..74..187S. doi :10.1119/1.2174962.
6. Swendsen, Robert H. (junio de 2002). "Mecánica estadística de sistemas clásicos con partículas distinguibles". Revista de Física Estadística . 107 (5/6): 1143-1166. Código Bib : 2002JSP...107.1143S. doi :10.1023/A:1015161825292. S2CID  122463989.
7. Jaynes, et (1992). La paradoja de Gibbs en la máxima entropía y los métodos bayesianos (editado por CR Smith, GJ Erickson y PO Neudorfere) (PDF) . Dordrecht, Holanda: Kluwer Academic Publishers. págs. 1–22. En particular, Gibbs no señaló que una "constante de integración" no era una constante arbitraria, sino una función arbitraria. Pero esto tiene, como veremos, consecuencias físicas no triviales. Lo que es notable no es que Gibbs no haya logrado enfatizar un delicado punto matemático en casi las últimas palabras que escribió; pero que durante los 80 años siguientes todos los escritores de libros de texto (excepto posiblemente Pauli) no lograron verlo.

Otras lecturas

• Chih-Yuan Tseng y Ariel Caticha (2001). "Otra resolución más de la paradoja de Gibbs: un enfoque de la teoría de la información". En RL Fry (ed.). Métodos de inferencia bayesiana y máxima entropía en ciencia e ingeniería . Actas de la conferencia AIP. vol. 617. pág. 331. arXiv : cond-mat/0109324 . doi : 10.1063/1.1477057.
• Dieks, Dennis (2011). "La paradoja de Gibbs revisitada". En Dennis Dieks; Wenceslao J. González; Stéphan Hartmann ; Tomás Uebel; Marcel Weber (eds.). Explicación, Predicción y Confirmación . La filosofía de la ciencia en una perspectiva europea. págs. 367–377. arXiv : 1003.0179 . doi :10.1007/978-94-007-1180-8_25. ISBN 978-94-007-1179-2. S2CID  118395415.

enlaces externos

• La paradoja de Gibbs y sus resoluciones: diversos artículos recopilados