Inmersión (matemáticas)

Función diferenciable cuya derivada es en todas partes inyectiva

La botella de Klein , sumergida en tres espacios.

En matemáticas , una inmersión es una función diferenciable entre variedades diferenciables cuyo empuje diferencial hacia delante es en todas partes inyectivo . ^[1] Explícitamente, f  : M → N es una inmersión si

${\displaystyle D_{p}f:T_{p}M\to T_{f(p)}N\,}$

es una función inyectiva en cada punto p de M (donde T _p X denota el espacio tangente de una variedad X en un punto p en X y D _p f es la derivada (avanzada) de la función f en el punto p ). De manera equivalente, f es una inmersión si su derivada tiene rango constante igual a la dimensión de M : ^[2]

${\displaystyle \operatorname {rank} \,D_{p}f=\dim M.}$

La función f en sí no necesita ser inyectiva, sólo su derivada debe serlo.

Vs. incrustación

Un concepto relacionado es el de incrustación . Una incrustación suave es una inmersión inyectiva f  : M → N que también es una incrustación topológica , de modo que M es difeomórfica con respecto a su imagen en N. Una inmersión es precisamente una incrustación local , es decir, para cualquier punto x ∈ M hay un entorno , U ⊆ M , de x tal que f  : U → N es una incrustación y, a la inversa, una incrustación local es una inmersión. ^[3] Para variedades de dimensión infinita, a veces se considera que esta es la definición de una inmersión. ^[4]

Una subvariedad inyectivamente sumergida que no es una incrustación.

Si M es compacto , una inmersión inyectiva es una incrustación, pero si M no es compacto, entonces las inmersiones inyectivas no necesitan ser incrustaciones; compárese con biyecciones continuas versus homeomorfismos .

Homotopía regular

Una homotopía regular entre dos inmersiones f y g desde una variedad M a una variedad N se define como una función diferenciable H  : M × [0,1] → N tal que para todo t en [0, 1] la función H _t  : M → N definida por H _t ( x ) = H ( x , t ) para todo x ∈ M es una inmersión, con H ₀ = f , H ₁ = g . Una homotopía regular es, por tanto, una homotopía a través de inmersiones.

Clasificación

Hassler Whitney inició el estudio sistemático de inmersiones y homotopías regulares en la década de 1940, demostrando que para 2 m < n + 1 toda función f  : M ^m → N ⁿ de una variedad m -dimensional a una variedad n -dimensional es homotópica a una inmersión, y de hecho a una incrustación para 2 m < n ; estos son el teorema de inmersión de Whitney y el teorema de incrustación de Whitney .

Stephen Smale expresó las clases de homotopía regulares de inmersiones como los ${\displaystyle f:M^{m}\to \mathbb {R} ^{n}}$ grupos de homotopía de una cierta variedad de Stiefel . La eversión de la esfera fue una consecuencia particularmente sorprendente.

Morris Hirsch generalizó la expresión de Smale a una descripción de la teoría de homotopía de las clases de homotopía regulares de inmersiones de cualquier variedad m -dimensional M ^m en cualquier variedad n -dimensional N ⁿ .

La clasificación de inmersiones de Hirsch-Smale fue generalizada por Mikhail Gromov .

Existencia

La banda de Möbius no se sumerge en la codimensión 0 porque su fibrado tangente no es trivial.

El principal obstáculo a la existencia de una inmersión ⁠ ⁠ ${\displaystyle i:M^{m}\to \mathbb {R} ^{n}}$ es el fibrado normal estable de M , detectado por sus clases características , en particular sus clases de Stiefel–Whitney . Es decir, dado que ⁠ ⁠ ${\displaystyle \mathbb {R} ^{n}}$ es paralelizable , el pullback de su fibrado tangente a M es trivial; dado que este pullback es la suma directa del fibrado tangente (intrínsecamente definido) en M , TM , que tiene dimensión m , y del fibrado normal ν de la inmersión i , que tiene dimensión n − m , para que haya una inmersión de codimensión k de M , debe haber un fibrado vectorial de dimensión k , ξ ^k , que sustituya al fibrado normal ν , tal que ⁠ ⁠ ${\displaystyle TM\oplus \zeta ^{k}}$ sea trivial. Por el contrario, dado tal fibrado, una inmersión de M con este fibrado normal es equivalente a una inmersión de codimensión 0 del espacio total de este fibrado, que es una variedad abierta.

El fibrado normal estable es la clase de fibrados normales más fibrados triviales y, por lo tanto, si el fibrado normal estable tiene dimensión cohomológica k , no puede provenir de un fibrado normal (inestable) de dimensión menor que k . Por lo tanto, la dimensión cohomológica del fibrado normal estable, detectada por su clase característica no nula más alta, es una obstrucción a las inmersiones.

Dado que las clases características se multiplican bajo la suma directa de fibrados vectoriales, esta obstrucción puede enunciarse intrínsecamente en términos del espacio M y su fibrado tangente y del álgebra de cohomología. Esta obstrucción fue enunciada (en términos del fibrado tangente, no del fibrado normal estable) por Whitney.

Por ejemplo, la banda de Möbius tiene un fibrado tangente no trivial, por lo que no puede sumergirse en la codimensión 0 (en ⁠ ⁠ ${\displaystyle \mathbb {R} ^{2}}$ ), aunque sí se incrusta en la codimensión 1 (en ⁠ ⁠ ${\displaystyle \mathbb {R} ^{3}}$ ).

William S. Massey  (1960) demostró que estas clases características (las clases de Stiefel–Whitney del fibrado normal estable) se desvanecen por encima del grado n − α ( n ) , donde α ( n ) es el número de dígitos "1" cuando n se escribe en binario; este límite es preciso, como se desprende del espacio proyectivo real . Esto proporcionó evidencia de la conjetura de inmersión , es decir, que cada n -variedad podría sumergirse en la codimensión n − α ( n ) , es decir, en ⁠ ⁠ ${\displaystyle \mathbb {R} ^{2n-\alpha (n)}.}$ Esta conjetura fue demostrada por Ralph Cohen  (1985).

Codimensión 0

Las inmersiones de codimensión 0 son equivalentemente inmersiones de dimensión relativa 0 y es mejor considerarlas como inmersiones. Una inmersión de codimensión 0 de una variedad cerrada es precisamente un mapa de recubrimiento , es decir, un haz de fibras con fibra de dimensión 0 (discreta). Por el teorema de Ehresmann y el teorema de Phillips sobre inmersiones, una inmersión propia de variedades es un haz de fibras, por lo tanto, las inmersiones/inmersiones de codimensión/dimensión relativa 0 se comportan como inmersiones.

Además, las inmersiones de codimensión 0 no se comportan como otras inmersiones, que están determinadas en gran medida por el fibrado normal estable: en la codimensión 0 uno tiene problemas de clase fundamental y espacios de cobertura. Por ejemplo, no hay inmersión de codimensión 0 ⁠ ⁠ ${\displaystyle \mathbb {S} ^{1}\to \mathbb {R} ^{1},}$ a pesar de que el círculo es paralelizable, lo que se puede demostrar porque la línea no tiene clase fundamental, por lo que no se obtiene la función requerida en la cohomología superior. Alternativamente, esto es por invariancia del dominio . De manera similar, aunque ⁠ ⁠ ${\displaystyle \mathbb {S} ^{3}}$ y el 3-toro ⁠ ⁠ ${\displaystyle \mathbb {T} ^{3}}$ son ambos paralelizables, no hay inmersión ⁠ ⁠ ${\displaystyle \mathbb {T} ^{3}\to \mathbb {S} ^{3}}$ – cualquier cobertura de este tipo tendría que estar ramificada en algunos puntos, ya que la esfera está simplemente conexa.

Otra forma de entender esto es que una inmersión en codimensión k de una variedad corresponde a una inmersión en codimensión 0 de un fibrado vectorial de dimensión k , que es una variedad abierta si la codimensión es mayor que 0, pero a una variedad cerrada en codimensión 0 (si la variedad original es cerrada).

Puntos múltiples

Un punto k -tupla (doble, triple, etc.) de una inmersión f  : M → N es un conjunto no ordenado { x ₁ , ..., x _k } de puntos distintos x _i ∈ M con la misma imagen f ( x _i ) ∈ N . Si M es una variedad m -dimensional y N es una variedad n -dimensional entonces para una inmersión f  : M → N en posición general el conjunto de puntos k -tupla es una variedad ( n − k ( n − m )) -dimensional. Toda incrustación es una inmersión sin puntos múltiples (donde k > 1 ). Nótese, sin embargo, que lo inverso es falso: hay inmersiones inyectivas que no son incrustaciones.

La naturaleza de los puntos múltiples clasifica las inmersiones; por ejemplo, las inmersiones de un círculo en el plano se clasifican hasta la homotopía regular por el número de puntos dobles.

En un punto clave de la teoría de la cirugía es necesario decidir si una inmersión ⁠ ⁠ ${\displaystyle f:\mathbb {S} ^{m}\to N^{2m}}$ de una m -esfera en una variedad de 2 m -dimensional es homotópica regular a una incrustación, en cuyo caso puede ser eliminada mediante cirugía. Wall asoció a f un invariante μ ( f ) en un cociente del anillo de grupo fundamental ⁠ ⁠ ${\displaystyle \mathbb {Z} [\pi _{1}(N)]}$ que cuenta los puntos dobles de f en la cubierta universal de N . Para m > 2 , f es homotópica regular a una incrustación si y solo si μ ( f ) = 0 por el truco de Whitney .

Se pueden estudiar las incrustaciones como "inmersiones sin puntos múltiples", ya que las inmersiones son más fáciles de clasificar. Por lo tanto, se puede partir de inmersiones e intentar eliminar puntos múltiples, viendo si se puede hacer esto sin introducir otras singularidades, estudiando "disyunciones múltiples". Esto fue realizado por primera vez por André Haefliger , y este enfoque es fructífero en la codimensión 3 o más: desde el punto de vista de la teoría de la cirugía, esta es una "alta (co)dimensión", a diferencia de la codimensión 2 que es la dimensión de anudado, como en la teoría de nudos . Se estudia categóricamente a través del " cálculo de funtores " de Thomas Goodwillie Archivado el 28 de noviembre de 2009 en Wayback Machine , John Klein y Michael S. Weiss.

Ejemplos y propiedades

El cuadrifolio , la rosa de 4 pétalos.

• Una rosa matemática con k pétalos es una inmersión del círculo en el plano con un único punto k -tupla; k puede ser cualquier número impar, pero si es par debe ser múltiplo de 4, por lo que la figura 8, con k = 2 , no es una rosa.
• La botella de Klein , y todas las demás superficies cerradas no orientables, se pueden sumergir en el espacio tridimensional pero no incrustar.
• Por el teorema de Whitney-Graustein , las clases de homotopía regular de inmersiones del círculo en el plano se clasifican por el número de enrollamiento , que es también el número de puntos dobles contados algebraicamente (es decir, con signos).
• La esfera se puede girar al revés : la incrustación estándar está relacionada ${\displaystyle f_{0}:\mathbb {S} ^{2}\to \mathbb {R} ^{3}}$ con una homotopía regular de inmersiones . ${\displaystyle f_{1}=-f_{0}:\mathbb {S} ^{2}\to \mathbb {R} ^{3}}$ ${\displaystyle f_{t}:\mathbb {S} ^{2}\to \mathbb {R} ^{3}.}$
• La superficie del niño es una inmersión del plano proyectivo real en el espacio tridimensional; por tanto, también es una inmersión 2 a 1 de la esfera.
• La superficie de Morin es una inmersión de la esfera; tanto ésta como la superficie de Boy surgen como modelos intermedios en la eversión de la esfera.

• Superficie del niño
• La superficie de Morin

Curvas planas inmersas

Esta curva tiene una curvatura total  de 6 π y un giro número  3, aunque sólo tiene el giro número  2 alrededor de  p .

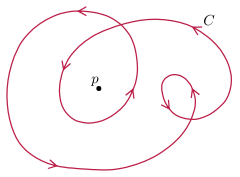
Las curvas planas inmersas tienen un número de giro bien definido , que se puede definir como la curvatura total dividida por 2 π . Este es invariante bajo homotopía regular, por el teorema de Whitney-Graustein – topológicamente, es el grado de la función de Gauss , o equivalentemente el número de giro de la tangente unitaria (que no se anula) alrededor del origen. Además, este es un conjunto completo de invariantes – cualesquiera dos curvas planas con el mismo número de giro son homotópicas regulares.

Toda curva plana sumergida se eleva hasta convertirse en una curva espacial incrustada mediante la separación de los puntos de intersección, lo que no es cierto en dimensiones superiores. Con datos añadidos (qué hebra está en la parte superior), las curvas planas sumergidas producen diagramas de nudos , que son de interés central en la teoría de nudos . Si bien las curvas planas sumergidas, hasta la homotopía regular, están determinadas por su número de giros, los nudos tienen una estructura muy rica y compleja.

Superficies inmersas en 3 espacios

El estudio de superficies sumergidas en el espacio tridimensional está estrechamente relacionado con el estudio de superficies anudadas (incrustadas) en el espacio cuádruple, por analogía con la teoría de los diagramas de nudos (curvas planas sumergidas (espacios bidimensionales) como proyecciones de curvas anudadas en el espacio tridimensional): dada una superficie anudada en el espacio cuádruple, se la puede proyectar a una superficie sumergida en el espacio tridimensional y, a la inversa, dada una superficie sumergida en el espacio tridimensional, se puede preguntar si se eleva al espacio cuádruple: ¿es la proyección de una superficie anudada en el espacio cuádruple? Esto permite relacionar preguntas sobre estos objetos.

Un resultado básico, en contraste con el caso de las curvas planas, es que no toda superficie sumergida se eleva hasta una superficie anudada. ^[5] En algunos casos la obstrucción es 2-torsión, como en el ejemplo de Koschorke , ^[6] que es una superficie sumergida (formada a partir de 3 bandas de Möbius, con un punto triple ) que no se eleva hasta una superficie anudada, pero tiene una doble cubierta que sí se eleva. Se da un análisis detallado en Carter & Saito (1998a), mientras que un estudio más reciente se da en Carter, Kamada & Saito (2004).

Generalizaciones

Una generalización de gran alcance de la teoría de la inmersión es el principio de homotopía : se puede considerar la condición de inmersión (el rango de la derivada es siempre k ) como una relación diferencial parcial (PDR), ya que puede enunciarse en términos de las derivadas parciales de la función. Entonces, la teoría de inmersión de Smale-Hirsch es el resultado de que esto se reduce a la teoría de la homotopía, y el principio de homotopía proporciona condiciones generales y razones para que las PDR se reduzcan a la teoría de la homotopía.

Véase también

• Subvariedad inmersa
• Inmersión isométrica
• Sumersión

Notas

1. Esta definición la dan Bishop & Crittenden 1964, p. 185, cariño 1994, pág. 53, do Carmo 1994, p. 11, Frankel 1997, pág. 169, Gallot, Hulin y Lafontaine 2004, pág. 12, Kobayashi y Nomizu 1963, pág. 9, Kosinski 2007, pág. 27, Székeres 2004, pág. 429.
2. Esta definición la dan Crampin y Pirani 1994, p. 243, Spivak 1999, p. 46.
3. Este tipo de definición, basada en difeomorfismos locales, la dan Bishop & Goldberg 1968, p. 40, Lang 1999, p. 26.
4. Este tipo de definición de dimensión infinita la da Lang 1999, p. 26.
5. Carter y Saito 1998; Carter, Kamada y Saito 2004, Observación 1.23, pág. 17
6. Koschorke 1979

Referencias

• Adachi, Masahisa (1993), Incrustaciones e inmersiones, traducido por Kiki Hudson, ISBN 978-0-8218-4612-4
• Arnoldo, VI ; Varchenko, AN; Gusein-Zade, SM (1985), Singularidades de mapas diferenciables: volumen 1 , Birkhäuser, ISBN 0-8176-3187-9
• Bishop, Richard Lawrence ; Crittenden, Richard J. (1964), Geometría de variedades , Nueva York: Academic Press, ISBN 978-0-8218-2923-3
• Bishop, RL ; Goldberg, SI (1968), Análisis tensorial en variedades (Primera edición de Dover 1980), The Macmillan Company, ISBN 0-486-64039-6
• Bruce, JW; Giblin, PJ (1984), Curvas y singularidades , Cambridge University Press, ISBN 0-521-42999-4
• Carter, J. Scott; Saito, Masahico (1998a), "Superficies en el espacio tridimensional que no se elevan hasta incrustaciones en el espacio cuádruple", Knot theory (Varsovia, 1995) , Banach Center Publ., vol. 42, Polish Acad. Sci., Varsovia, págs. 29–47, CiteSeerX  10.1.1.44.1505 , MR  1634445.
• Carter, J. Scott; Saito, Masahico (1998), Superficies anudadas y sus diagramas , Mathematical Surveys and Monographs, vol. 55, pág. 258, ISBN 978-0-8218-0593-0
• Carter, Scott; Kamada, Seiichi; Saito, Masahico (2004), Superficies en 4 espacios , Enciclopedia de Ciencias Matemáticas, vol. 142, Berlín: Springer-Verlag, doi :10.1007/978-3-662-10162-9, ISBN 3-540-21040-7, Sr.  2060067.
• Cohen, Ralph L. (1985), "La conjetura de inmersión para variedades diferenciables", Anales de Matemáticas , Segunda serie, 122 (2): 237–328, doi :10.2307/1971304, JSTOR  1971304, MR  0808220.
• Crampin, Michael; Pirani, Felix Arnold Edward (1994), Geometría diferencial aplicable , Cambridge, Inglaterra: Cambridge University Press, ISBN 978-0-521-23190-9
• Darling, Richard William Ramsay (1994), Formas diferenciales y conexiones , Cambridge, Reino Unido: Cambridge University Press, Bibcode :1994dfc..book.....D, ISBN 978-0-521-46800-8.
• do Carmo, Manfredo Perdigao (1994), Geometría riemanniana , ISBN 978-0-8176-3490-2
• Frankel, Theodore (1997), La geometría de la física , Cambridge: Cambridge University Press, ISBN 0-521-38753-1
• Gallot, Sylvestre; Hulin, Dominique ; Lafontaine, Jacques (2004), Geometría de Riemann (3.ª ed.), Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-20493-0
• Gromov, M. (1986), Relaciones diferenciales parciales , Springer, ISBN 3-540-12177-3
• Hirsch, Morris W. (1959), "Inmersiones de variedades", Transactions of the American Mathematical Society , 93 (2): 242–276, doi : 10.2307/1993453 , JSTOR  1993453, MR  0119214.
• Kobayashi, Shoshichi; Nomizu, Katsumi (1963), Fundamentos de geometría diferencial, Volumen 1 , Nueva York: Wiley-Interscience
• Koschorke, Ulrich (1979), "Múltiples puntos de inmersiones y el teorema de Kahn-Priddy", Mathematische Zeitschrift , 169 (3): 223–236, doi :10.1007/BF01214837, MR  0554526, S2CID  121273182.
• Kosinski, Antoni Albert (2007) [1993], Variedades diferenciales , Mineola, Nueva York: Dover Publications, ISBN 978-0-486-46244-8
• Lang, Serge (1999), Fundamentos de geometría diferencial , Textos de posgrado en matemáticas, Nueva York: Springer, ISBN 978-0-387-98593-0
• Massey, WS (1960), "Sobre las clases de Stiefel-Whitney de una variedad", American Journal of Mathematics , 82 (1): 92–102, doi :10.2307/2372878, JSTOR  2372878, MR  0111053.
• Smale, Stephen (1958), "Una clasificación de las inmersiones de las dos esferas", Transactions of the American Mathematical Society , 90 (2): 281–290, doi : 10.2307/1993205 , JSTOR  1993205, MR  0104227.
• Smale, Stephen (1959), "La clasificación de inmersiones de esferas en espacios euclidianos", Anales de Matemáticas , Segunda Serie, 69 (2): 327–344, doi :10.2307/1970186, JSTOR  1970186, MR  0105117.
• Spivak, Michael (1999) [1970], Una introducción completa a la geometría diferencial (volumen 1) , Publish or Perish, ISBN 0-914098-70-5
• Spring, David (2005), "La edad de oro de la teoría de la inmersión en topología: 1959-1973: un estudio matemático desde una perspectiva histórica", Boletín de la American Mathematical Society , Nueva serie, 42 (2): 163-180, CiteSeerX  10.1.1.363.913 , doi :10.1090/S0273-0979-05-01048-7, MR  2133309, S2CID  9237068.
• Szekeres, Peter (2004), Un curso de física matemática moderna: grupos, espacio de Hilbert y geometría diferencial , Cambridge, Reino Unido: Cambridge University Press, ISBN 978-0-521-82960-1
• Wall, CTC (1999), Cirugía en variedades compactas (PDF) , Mathematical Surveys and Monographs, vol. 69 (segunda ed.), Providence, RI: American Mathematical Society, doi : 10.1090/surv/069, ISBN 0-8218-0942-3, Sr.  1687388.

Enlaces externos

• Inmersión en el Atlas Manifold
• Inmersión de una variedad en la Enciclopedia de Matemáticas