Modelo XY clásico

Modelo reticular de la mecánica estadística

El modelo XY clásico (a veces también llamado modelo de rotor clásico o modelo O(2) ) es un modelo reticular de mecánica estadística . En general , el modelo XY puede verse como una especialización del modelo n -vectorial de Stanley ^[1] para n = 2 .

Definición

Dada una red D -dimensional Λ , por cada sitio de red j ∈ Λ hay un vector bidimensional de longitud unitaria s _j = (cos θ _j , sin θ _j )

La configuración de espín , s = ( s _j ) _{j ∈ Λ} es una asignación del ángulo − π < θ _j ≤ π para cada j ∈ Λ .

Dada una interacción invariante de traslación J _ij = J ( i − j ) y un campo externo dependiente del punto , la energía de configuración es ${\displaystyle \mathbf {h} _{j}=(h_{j},0)}$

${\displaystyle H(\mathbf {s} )=-\sum _{i\neq j}J_{ij}\;\mathbf {s} _{i}\cdot \mathbf {s} _{j}-\sum _{j}\mathbf {h} _{j}\cdot \mathbf {s} _{j}=-\sum _{i\neq j}J_{ij}\;\cos(\theta _{i}-\theta _{j})-\sum _{j}h_{j}\cos \theta _{j}}$

El caso en el que J _ij = 0 excepto ij vecino más cercano se llama caso de vecino más cercano .

La probabilidad de configuración viene dada por la distribución de Boltzmann con temperatura inversa β ≥ 0 :

${\displaystyle P(\mathbf {s} )={\frac {e^{-\beta H(\mathbf {s} )}}{Z}}\qquad Z=\int _{[-\pi ,\pi ]^{\Lambda }}\prod _{j\in \Lambda }d\theta _{j}\;e^{-\beta H(\mathbf {s} )}.}$

donde Z es la función de normalización o partición . ^[2] La notación indica la expectativa de la variable aleatoria A ( s ) en el límite de volumen infinito, después de que se han impuesto condiciones de contorno periódicas . ${\displaystyle \langle A(\mathbf {s} )\rangle }$

Resultados rigurosos

• La existencia del límite termodinámico para las correlaciones de energía libre y espín fue demostrada por Ginibre , extendiendo a este caso la desigualdad de Griffiths . ^[3]
• Utilizando la desigualdad de Griffiths en la formulación de Ginibre, Aizenman y Simon ^[4] demostraron que la correlación de espín de dos puntos del modelo ferromagnético XY en la dimensión D , acoplamiento J > 0 y temperatura inversa β está dominada por (es decir, tiene un límite superior dado por) la correlación de dos puntos del modelo ferromagnético de Ising en la dimensión D , acoplamiento J > 0 y temperatura inversa ⁠β/2⁠ Por lo tanto, la β crítica del modelo XY no puede ser menor que el doble de la temperatura crítica del modelo de Ising. $${\displaystyle \langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle _{J,2\beta }\leq \langle \sigma _{i}\sigma _{j}\rangle _{J,\beta }}$$ $${\displaystyle \beta _{c}^{XY}\geq 2\beta _{c}^{\rm {Is}}}$$

Una dimensión

Como en cualquier modelo n -vectorial de "vecino más cercano" con condiciones de contorno libres (no periódicas), si el campo externo es cero, existe una solución exacta simple. En el caso de condiciones de contorno libres, el hamiltoniano es, por lo tanto, la función de partición se factoriza bajo el cambio de coordenadas Esto da donde es la función de Bessel modificada de primera clase. La función de partición se puede utilizar para encontrar varias cantidades termodinámicas importantes. Por ejemplo, en el límite termodinámico ( ), la energía libre por espín es Utilizando las propiedades de las funciones de Bessel modificadas, el calor específico (por espín) se puede expresar como ^[5] donde , y es la función de correlación de corto alcance, $${\displaystyle H(\mathbf {s} )=-J[\cos(\theta _{1}-\theta _{2})+\cdots +\cos(\theta _{L-1}-\theta _{L})]}$$ $${\displaystyle \theta _{j}=\theta _{j}'+\theta _{j-1}\qquad j\geq 2}$$ $${\displaystyle {\begin{aligned}Z&=\int _{-\pi }^{\pi }d\theta _{1}\cdots d\theta _{L}\;e^{\beta J\cos(\theta _{1}-\theta _{2})}\cdots e^{\beta J\cos(\theta _{L-1}-\theta _{L})}\\&=2\pi \prod _{j=2}^{L}\int _{-\pi }^{\pi }d\theta '_{j}\;e^{\beta J\cos \theta '_{j}}=(2\pi )\left[\int _{-\pi }^{\pi }d\theta '_{j}\;e^{\beta J\cos \theta '_{j}}\right]^{L-1}=(2\pi )^{L}(I_{0}(\beta J))^{L-1}\end{aligned}}}$$ ${\displaystyle I_{0}}$ ${\displaystyle L\to \infty }$ $${\displaystyle f(\beta ,h=0)=-\lim _{L\to \infty }{\frac {1}{\beta L}}\ln Z=-{\frac {1}{\beta }}\ln[2\pi I_{0}(\beta J)]}$$ $${\displaystyle {\frac {c}{k_{\rm {B}}}}=\lim _{L\to \infty }{\frac {1}{L(k_{\rm {B}}T)^{2}}}{\frac {\partial ^{2}}{\partial \beta ^{2}}}(\ln Z)=K^{2}\left(1-{\frac {\mu }{K}}-\mu ^{2}\right)}$$ ${\displaystyle K=J/k_{\rm {B}}T}$ ${\displaystyle \mu }$

Calor específico exacto por espín en el modelo XY unidimensional

$${\displaystyle \mu (K)=\langle \cos(\theta -\theta ')\rangle ={\frac {I_{1}(K)}{I_{0}(K)}}}$$

Incluso en el límite termodinámico, no hay divergencia en el calor específico. De hecho, al igual que el modelo unidimensional de Ising, el modelo unidimensional XY no tiene transiciones de fase a temperatura finita.

El mismo cálculo para la condición de contorno periódica (y todavía h = 0 ) requiere el formalismo de matriz de transferencia , aunque el resultado es el mismo. ^[6]

(Haga clic en "mostrar" a la derecha para ver los detalles del formalismo de la matriz de transferencia).

La función de partición se puede evaluar como que puede tratarse como la traza de una matriz, es decir, un producto de matrices (escalares, en este caso). La traza de una matriz es simplemente la suma de sus valores propios, y en el límite termodinámico solo sobrevivirá el valor propio más grande, por lo que la función de partición se puede escribir como un producto repetido de este valor propio máximo. Esto requiere resolver el problema del valor propio. Nótese la expansión $${\displaystyle Z={\text{tr}}\left\{\prod _{i=1}^{N}\oint d\theta _{i}e^{\beta J\cos(\theta _{i}-\theta _{i+1})}\right\}}$$ ${\displaystyle L\to \infty }$ $${\displaystyle \oint d\theta '\exp\{\beta J\cos(\theta '-\theta )\}\psi (\theta ')=z_{i}\psi (\theta )}$$ $${\displaystyle \exp\{\beta J\cos(\theta -\theta ')\}=\sum _{n=-\infty }^{\infty }I_{n}(\beta J)e^{in(\theta -\theta ')}=\sum _{n=-\infty }^{\infty }\omega _{n}\psi _{n}^{*}(\theta ')\psi _{n}(\theta )}$$

que representa una representación matricial diagonal en base a sus funciones propias de onda plana . Los valores propios de la matriz son simplemente funciones de Bessel modificadas evaluadas en , es decir . Para cualquier valor particular de , estas funciones de Bessel modificadas satisfacen y . Por lo tanto, en el límite termodinámico, el valor propio dominará la traza, y por lo tanto . ${\displaystyle \psi =\exp(in\theta )}$ ${\displaystyle \beta J}$ ${\displaystyle \omega _{n}=2\pi I_{n}(\beta J)}$ ${\displaystyle \beta J}$ ${\displaystyle I_{0}>I_{1}>I_{2}>\cdots }$ ${\displaystyle I_{-n}(\beta J)=I_{n}(\beta J)}$ ${\displaystyle I_{0}}$ ${\displaystyle Z=[2\pi I_{0}(\beta J)]^{L}}$

Este enfoque de matriz de transferencia también se requiere cuando se utilizan condiciones de contorno libres, pero con un campo aplicado . Si el campo aplicado es lo suficientemente pequeño como para que pueda tratarse como una perturbación del sistema en campo cero, entonces se puede estimar la susceptibilidad magnética . Esto se hace utilizando los estados propios calculados por el enfoque de matriz de transferencia y calculando el cambio de energía con la teoría de perturbación de segundo orden , luego comparando con la expansión de energía libre . Se encuentra ^[7] donde es la constante de Curie (un valor típicamente asociado con la susceptibilidad en materiales magnéticos). Esta expresión también es verdadera para el modelo de Ising unidimensional, con el reemplazo . ${\displaystyle h\neq 0}$ ${\displaystyle h}$ ${\displaystyle \chi \equiv \partial M/\partial h}$ ${\displaystyle F=F_{0}-{\frac {1}{2}}\chi h^{2}}$ $${\displaystyle \chi (h\to 0)={\frac {C}{T}}{\frac {1+\mu }{1-\mu }}}$$ ${\displaystyle C}$ ${\displaystyle \mu =\tanh K}$

Dos dimensiones

Magnetización cuadrática media para una red de 25x25 (Ota: ^[8] 30x30), lo que sugiere un aumento del momento magnético que no está presente en el límite termodinámico

El modelo XY bidimensional con interacciones de vecinos más cercanos es un ejemplo de un sistema bidimensional con simetría continua que no tiene orden de largo alcance. Asimismo, no hay una transición de fase convencional presente que estaría asociada con la ruptura de la simetría . Sin embargo, como se discutirá más adelante, el sistema muestra signos de una transición de un estado desordenado de alta temperatura a un estado cuasiordenado por debajo de cierta temperatura crítica, llamada la transición de Kosterlitz-Thouless . En el caso de una red discreta de espines, el modelo XY bidimensional se puede evaluar utilizando el enfoque de la matriz de transferencia, reduciendo el modelo a un problema de valor propio y utilizando el valor propio más grande de la matriz de transferencia. Aunque la solución exacta es intratable, es posible utilizar ciertas aproximaciones para obtener estimaciones de la temperatura crítica que ocurre a bajas temperaturas. Por ejemplo, Mattis (1984 ^[9] ) utilizó una aproximación a este modelo para estimar una temperatura crítica del sistema como El modelo 2D XY también se ha estudiado en gran detalle utilizando simulaciones de Monte Carlo , por ejemplo con el algoritmo Metropolis . Estos se pueden utilizar para calcular cantidades termodinámicas como la energía del sistema, el calor específico, la magnetización, etc., en un rango de temperaturas y escalas de tiempo. En la simulación de Monte Carlo, cada giro está asociado a un ángulo que varía continuamente (a menudo, se puede discretizar en un número finito de ángulos, como en el modelo relacionado de Potts , para facilitar el cálculo. Sin embargo, esto no es un requisito). En cada paso de tiempo, el algoritmo Metropolis elige un giro al azar y rota su ángulo en algún incremento aleatorio . Este cambio en el ángulo provoca un cambio en la energía del sistema, que puede ser positivo o negativo. Si es negativo, el algoritmo acepta el cambio en el ángulo; si es positivo, la configuración se acepta con probabilidad , el factor de Boltzmann para el cambio de energía. El método de Monte Carlo se ha utilizado para verificar, con varios métodos, la temperatura crítica del sistema, y ​​se estima que es ^[10] . El método de Monte Carlo también puede calcular valores promedio que se utilizan para calcular cantidades termodinámicas como la magnetización, la correlación espín-espín, las longitudes de correlación y el calor específico. Estas son formas importantes de caracterizar el comportamiento del sistema cerca de la temperatura crítica. La magnetización y la magnetización al cuadrado, por ejemplo, se pueden calcular como ${\displaystyle T_{c}}$ $${\displaystyle (2k_{\rm {B}}T_{c}/J)\ln(2k_{\rm {B}}T_{c}/J)=1}$$ $${\displaystyle k_{\rm {B}}T_{c}/J\approx 0.8816}$$ ${\displaystyle \theta _{i}}$ ${\displaystyle \Delta \theta _{i}\in (-\Delta ,\Delta )}$ ${\displaystyle \Delta E_{i}}$ ${\displaystyle e^{-\beta \Delta E_{i}}}$ ${\displaystyle k_{\rm {B}}T_{c}/J=0.8935(1)}$

Calor específico del modelo XY bidimensional, calculado mediante simulación de Monte Carlo en redes cuadradas de tamaño de hasta 4096 x 4096 (Nguyen: ^[11] ), que muestra una característica en , por encima de la transición KT . El recuadro muestra la posición del pico en función del tamaño de la red. ${\displaystyle k_{\rm {B}}T/J\approx 1.167}$

$${\displaystyle {\frac {\langle M\rangle }{N}}={\frac {1}{N}}|\langle \mathbf {s} \rangle |={\frac {1}{N}}\left|\left\langle \left(\sum _{i=1}^{N}\cos \theta _{i},\sum _{i=1}^{N}\sin \theta _{i}\right)\right\rangle \right|}$$ $${\displaystyle {\frac {\langle M^{2}\rangle }{N^{2}}}={\frac {1}{N^{2}}}\left\langle s_{x}^{2}+s_{y}^{2}\right\rangle ={\frac {1}{N^{2}}}\left\langle \left(\sum _{i=1}^{N}\cos \theta _{i}\right)^{2}+\left(\sum _{i=1}^{N}\sin \theta _{i}\right)^{2}\right\rangle }$$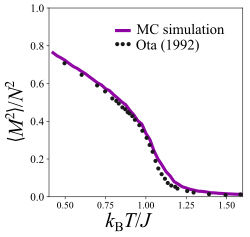donde son el número de espines. La magnetización media caracteriza la magnitud del momento magnético neto del sistema; en muchos sistemas magnéticos esto es cero por encima de una temperatura crítica y se vuelve distinto de cero espontáneamente a bajas temperaturas. De manera similar, la magnetización cuadrática media caracteriza el promedio del cuadrado de los componentes netos de los espines a través de la red. Cualquiera de estos se usa comúnmente para caracterizar el parámetro de orden de un sistema. Un análisis riguroso del modelo XY muestra que la magnetización en el límite termodinámico es cero, y que la magnetización cuadrada sigue aproximadamente ^[12] , que se desvanece en el límite termodinámico. De hecho, a altas temperaturas esta cantidad se acerca a cero ya que los componentes de los espines tenderán a ser aleatorios y, por lo tanto, sumarán cero. Sin embargo, a bajas temperaturas para un sistema finito, la magnetización cuadrática media aumenta, lo que sugiere que hay regiones del espacio de espines que están alineadas para contribuir a una contribución distinta de cero. La magnetización mostrada (para una red de 25x25) es un ejemplo de esto, que parece sugerir una transición de fase, mientras que tal transición no existe en el límite termodinámico. ${\displaystyle N=L\times L}$ ${\displaystyle \langle M^{2}\rangle \approx N^{-T/4\pi }}$

Además, utilizando la mecánica estadística se pueden relacionar los promedios termodinámicos con cantidades como el calor específico calculando El calor específico se muestra a bajas temperaturas cerca de la temperatura crítica . No hay ninguna característica en el calor específico consistente con el comportamiento crítico (como una divergencia) a esta temperatura predicha. De hecho, la estimación de la temperatura crítica proviene de otros métodos, como el módulo de helicidad o la dependencia de la temperatura de la divergencia de la susceptibilidad. ^[13] Sin embargo, hay una característica en el calor específico en forma de un pico en . Se ha demostrado que esta posición y altura del pico no dependen del tamaño del sistema, para redes de tamaño lineal mayor que 256; de hecho, la anomalía del calor específico permanece redondeada y finita para un tamaño de red creciente, sin pico divergente. $${\displaystyle c/k_{\rm {B}}={\frac {\langle E^{2}\rangle -\langle E\rangle ^{2}}{N(k_{\rm {B}}T)^{2}}}}$$ ${\displaystyle k_{\rm {B}}T_{c}/J\approx 0.88}$ ${\displaystyle 1.167(1)k_{\rm {B}}T/J}$

La naturaleza de las transiciones críticas y la formación de vórtices se pueden dilucidar considerando una versión continua del modelo XY. Aquí, los espines discretos se reemplazan por un campo que representa el ángulo del espín en cualquier punto del espacio. En este caso, el ángulo de los espines debe variar suavemente con los cambios de posición. Al expandir el coseno original como una serie de Taylor , el hamiltoniano se puede expresar en la aproximación continua como ${\displaystyle \theta _{n}}$ ${\displaystyle \theta ({\textbf {x}})}$ ${\displaystyle \theta ({\textbf {x}})}$ $${\displaystyle E=\int {\frac {J}{2}}(\nabla \theta )^{2}\,d^{2}\mathbf {x} }$$

Mapa de colores del modelo XY bidimensional (discreto) en una red de 250x250 en . Cada giro está representado por un color que corresponde a un ángulo entre ${\displaystyle k_{\rm {B}}T/J=0.4}$ ${\displaystyle (-\pi ,\pi ]}$

La versión continua del modelo XY se utiliza a menudo para modelar sistemas que poseen parámetros de orden con los mismos tipos de simetría, por ejemplo, helio superfluido , cristales líquidos hexáticos. Esto es lo que los hace peculiares de otras transiciones de fase que siempre van acompañadas de una ruptura de simetría. Los defectos topológicos en el modelo XY conducen a una transición de desvinculación de vórtices de la fase de baja temperatura a la fase desordenada de alta temperatura . De hecho, el hecho de que a alta temperatura las correlaciones decaigan exponencialmente rápido, mientras que a bajas temperaturas decaen con la ley de potencia, aunque en ambos regímenes M ( β ) = 0 , se llama transición de Kosterlitz-Thouless . Kosterlitz y Thouless proporcionaron un argumento simple de por qué este sería el caso: esto considera el estado fundamental que consiste en todos los espines en la misma orientación, con la adición entonces de un solo vórtice. La presencia de estos contribuye a una entropía de aproximadamente , donde es una escala de longitud efectiva (por ejemplo, el tamaño de la red para una red discreta) Mientras tanto, la energía del sistema aumenta debido al vórtice, en una cantidad . Poniendo estos juntos, la energía libre de un sistema cambiaría debido a la formación espontánea de un vórtice en una cantidad En el límite termodinámico, el sistema no favorece la formación de vórtices a bajas temperaturas, pero sí los favorece a altas temperaturas, por encima de la temperatura crítica . Esto indica que a bajas temperaturas, cualquier vórtice que surja querrá aniquilarse con antivórtices para reducir la energía del sistema. De hecho, este será el caso cualitativamente si uno observa 'instantáneas' del sistema de espín a bajas temperaturas, donde los vórtices y los antivórtices se unen gradualmente para aniquilarse. Por lo tanto, el estado de baja temperatura consistirá en pares vórtice-antivórtice ligados. Mientras tanto, a altas temperaturas, habrá una colección de vórtices y antivórtices no unidos que serán libres de moverse por el plano. ${\displaystyle \Delta S=k_{\rm {B}}\ln(L^{2}/a^{2})}$ ${\displaystyle a}$ ${\displaystyle \Delta E=\pi J\ln(L/a)}$ $${\displaystyle \Delta F=\Delta E-T\Delta S=(\pi J-2k_{\rm {B}}T)\ln(L/a)}$$ ${\displaystyle T_{c}=\pi J/2k_{\rm {B}}}$

Para visualizar el modelo de Ising, se puede utilizar una flecha que apunta hacia arriba o hacia abajo, o bien se puede representar como un punto de color blanco y negro para indicar su estado. Para visualizar el sistema de espines XY, los espines se pueden representar como una flecha que apunta en alguna dirección, o como un punto con algún color. Aquí es necesario representar el espín con un espectro de colores debido a cada una de las posibles variables continuas. Esto se puede hacer utilizando, por ejemplo, un espectro continuo y periódico rojo-verde-azul. Como se muestra en la figura, el cian corresponde a un ángulo cero (apuntando hacia la derecha), mientras que el rojo corresponde a un ángulo de 180 grados (apuntando hacia la izquierda). A continuación, se pueden estudiar instantáneas de las configuraciones de espín a diferentes temperaturas para dilucidar lo que sucede por encima y por debajo de la temperatura crítica del modelo XY. A altas temperaturas, los espines no tendrán una orientación preferida y habrá una variación impredecible de los ángulos entre espines vecinos, ya que no habrá una configuración preferida energéticamente favorable. En este caso, el mapa de colores se verá muy pixelado. Mientras tanto, a bajas temperaturas, una posible configuración del estado fundamental tiene todos los espines apuntando en la misma orientación (mismo ángulo); estos corresponderían a regiones (dominios) del mapa de color donde todos los espines tienen aproximadamente el mismo color.

Varias formas de vórtices y antivórtices, mostradas en una simulación de Monte Carlo en ${\displaystyle k_{\rm {B}}T/J=0.4}$

Para identificar los vórtices (o antivórtices) presentes como resultado de la transición de Kosterlitz-Thouless, se puede determinar el cambio de ángulo con signo recorriendo un círculo de puntos de la red en sentido antihorario. Si el cambio total de ángulo es cero, esto corresponde a que no hay ningún vórtice presente; mientras que un cambio total de ángulo corresponde a un vórtice (o antivórtice). Estos vórtices son objetos topológicamente no triviales que se presentan en pares vórtice-antivórtice, que pueden separarse o aniquilarse en pares. En el mapa de colores, estos defectos se pueden identificar en regiones donde hay un gran gradiente de color donde todos los colores del espectro se encuentran alrededor de un punto. Cualitativamente, estos defectos pueden parecer fuentes de flujo que apuntan hacia adentro o hacia afuera, o remolinos de espines que colectivamente apuntan en el sentido de las agujas del reloj o en sentido contrario, o características de aspecto hiperbólico con algunos espines apuntando hacia y otros apuntando en dirección opuesta al defecto. A medida que se estudia la configuración en escalas de tiempo largas y a bajas temperaturas, se observa que muchos de estos pares de vórtices y antivórtices se acercan y terminan por aniquilarse. Solo a altas temperaturas estos vórtices y antivórtices se liberan y se desvinculan entre sí. ${\displaystyle \pm 2\pi }$

En el modelo XY continuo, la magnetización espontánea de alta temperatura desaparece: Además, la expansión del grupo muestra que las correlaciones de espín se agrupan exponencialmente rápido: por ejemplo , a bajas temperaturas, es decir, β ≫ 1 , la magnetización espontánea permanece cero (ver el teorema de Mermin-Wagner ), pero la descomposición de las correlaciones es solo una ley de potencia: Fröhlich y Spencer ^[14] encontraron el límite inferior $${\displaystyle M(\beta ):=|\langle \mathbf {s} _{i}\rangle |=0}$$ $${\displaystyle |\langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle |\leq C(\beta )e^{-c(\beta )|i-j|}}$$ $${\displaystyle M(\beta ):=|\langle \mathbf {s} _{i}\rangle |=0}$$

${\displaystyle |\langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle |\geq {\frac {C(\beta )}{1+|i-j|^{\eta (\beta )}}}}$

Mientras que McBryan y Spencer encontraron el límite superior, para cualquier ${\displaystyle \epsilon >0}$

${\displaystyle |\langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle |\leq {\frac {C(\beta ,\epsilon )}{1+|i-j|^{\eta (\beta ,\epsilon )}}}}$

Tres dimensiones y más

Independientemente del rango de interacción, a una temperatura suficientemente baja la magnetización es positiva.

• A alta temperatura, la magnetización espontánea desaparece: . Además, la expansión de cúmulos muestra que las correlaciones de espín se agrupan exponencialmente rápido: por ejemplo . ${\displaystyle M(\beta ):=|\langle \mathbf {s} _{i}\rangle |=0}$ ${\displaystyle |\langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle |\leq C(\beta )e^{-c(\beta )|i-j|}}$
• A baja temperatura, el límite infrarrojo muestra que la magnetización espontánea es estrictamente positiva: . Además, existe una familia de estados extremos de 1 parámetro, , tal que pero, conjeturalmente, en cada uno de estos estados extremos las correlaciones truncadas decaen algebraicamente. ${\displaystyle M(\beta ):=|\langle \mathbf {s} _{i}\rangle |>0}$ ${\displaystyle \langle \;\cdot \;\rangle ^{\theta }}$ ${\displaystyle \langle \mathbf {s} _{i}\rangle ^{\theta }=M(\beta )(\cos \theta ,\sin \theta )}$

Transición de fase

Como se mencionó anteriormente, en una dimensión, el modelo XY no tiene una transición de fase, mientras que en dos dimensiones tiene la transición Berezinski-Kosterlitz-Thouless entre las fases con funciones de correlación que decaen exponencialmente y en ley de potencia.

En tres dimensiones y superiores, el modelo XY presenta una transición de fase ferromagnética-paramagnética. A bajas temperaturas, la magnetización espontánea es distinta de cero: ésta es la fase ferromagnética. A medida que aumenta la temperatura, la magnetización espontánea disminuye gradualmente y desaparece en una temperatura crítica. Permanece cero a todas las temperaturas superiores: ésta es la fase paramagnética.

En cuatro dimensiones y superiores, la transición de fase tiene exponentes críticos de la teoría del campo medio (con correcciones logarítmicas en cuatro dimensiones).

Caso tridimensional: los exponentes críticos

El caso tridimensional es interesante porque los exponentes críticos en la transición de fase no son triviales. Muchos sistemas físicos tridimensionales pertenecen a la misma clase de universalidad que el modelo tridimensional XY y comparten los mismos exponentes críticos, en particular los imanes de plano fácil y el helio-4 líquido . Los valores de estos exponentes críticos se miden mediante experimentos, simulaciones de Monte Carlo y también se pueden calcular mediante métodos teóricos de la teoría cuántica de campos, como el grupo de renormalización y el bootstrap conforme . Los métodos del grupo de renormalización son aplicables porque se cree que el punto crítico del modelo XY está descrito por un punto fijo del grupo de renormalización. Los métodos de bootstrap conforme son aplicables porque también se cree que es una teoría de campo conforme tridimensional unitaria .

Los exponentes críticos más importantes del modelo tridimensional XY son . Todos ellos pueden expresarse mediante sólo dos números: las dimensiones de escala y del campo de parámetros de orden complejo y del operador singlete principal (igual que en la descripción de Ginzburg–Landau ). Otro campo importante es (igual que ), cuya dimensión determina el exponente de corrección a la escala . Según un cálculo bootstrap conforme, ^[15] estas tres dimensiones están dadas por: ${\displaystyle \alpha ,\beta ,\gamma ,\delta ,\nu ,\eta }$ ${\displaystyle \Delta _{\phi }}$ ${\displaystyle \Delta _{s}}$ ${\displaystyle \phi }$ ${\displaystyle s}$ ${\displaystyle |\phi |^{2}}$ ${\displaystyle s'}$ ${\displaystyle |\phi |^{4}}$ ${\displaystyle \Delta _{s'}}$ ${\displaystyle \omega }$

Esto da los siguientes valores de los exponentes críticos:

Los métodos de Monte Carlo proporcionan determinaciones compatibles: ^[16] . ${\displaystyle \eta =0.03810(8),\nu =0.67169(7),\omega =0.789(4)}$

Véase también

• Modelo clásico de Heisenberg
• Gas de Coulomb
• Bosón de Goldstone
• Modelo de Ising
• Modelo de Potts
• modelo n -vectorial
• Transición de Kosterlitz-Thouless
• Defecto topológico
• Película superfluida
• Modelo sigma
• Modelo de Sine-Gordon

Notas

1. Stanley, HE (1968). "Dependencia de las propiedades críticas de la dimensionalidad de los espines". Physical Review Letters . 20 (12): 589–592. Código Bibliográfico :1968PhRvL..20..589S. doi :10.1103/PhysRevLett.20.589.
2. Chaikin, PM; Lubensky, TC (2000). Principios de la física de la materia condensada. Cambridge University Press. ISBN 978-0521794503.
3. Ginibre, J. (1970). "Formulación general de las desigualdades de Griffiths". Communications in Mathematical Physics . 16 (4): 310–328. Bibcode :1970CMaPh..16..310G. doi :10.1007/BF01646537. S2CID  120649586.
4. Aizenman, M.; Simon, B. (1980). "Una comparación de los modelos de rotor plano e Ising". Physics Letters A . 76 (3–4): 281–282. Código Bibliográfico :1980PhLA...76..281A. doi :10.1016/0375-9601(80)90493-4.
5. Badalian, D. (1996). "Sobre la termodinámica de espines clásicos con interacción isótropa de Heisenberg en estructuras cuasiperiódicas unidimensionales". Physica B . 226 (4): 385–390. Bibcode :1996PhyB..226..385B. doi :10.1016/0921-4526(96)00283-9.
6. Mattis, DC (1984). "Matriz de transferencia en el modelo de rotador plano". Physics Letters A . 104 A (6–7): 357–360. Bibcode :1984PhLA..104..357M. doi :10.1016/0375-9601(84)90816-8.
7. Mattis, DC (1985). La teoría del magnetismo II . Springer Series in Solid-State Physics. ISBN 978-3-642-82405-0.
8. Ota, S.; Ota, SB; Fahnle, M (1992). "Simulaciones microcanónicas de Monte Carlo para el modelo XY bidimensional". Journal of Physics: Condensed Matter . 4 (24): 5411. Bibcode :1992JPCM....4.5411O. doi :10.1088/0953-8984/4/24/011. S2CID  250920391.
9. Mattis, Daniel (1984). "Matriz de transferencia en el modelo de rotador plano". Physics Letters A . 104 (6–7): 357–360.
10. Hsieh, Y.-D.; Kao, Y.-J.; Sandvik, AW (2013). "Método de escalamiento de tamaño finito para la transición Berezinskii-Kosterlitz-Thouless". Journal of Statistical Mechanics: Theory and Experiment . 2013 (9): P09001. arXiv : 1302.2900 . Código Bibliográfico :2013JSMTE..09..001H. doi :10.1088/1742-5468/2013/09/P09001. S2CID  118609225.
11. Nguyen, PH; Boninsegni, M. (2021). "Transición superfluida y calor específico del modelo xy 2D: simulación de Monte Carlo". Applied Sciences . 11 (11): 4931. arXiv : 2105.14112 . doi : 10.3390/app11114931 .
12. Tobochnik, J.; Chester, GV (1979). "Estudio de Monte Carlo del modelo de espín planar". Physical Review B . 20 (9): 3761–3769. Código Bibliográfico :1979PhRvB..20.3761T. doi :10.1103/PhysRevB.20.3761.
13. Binder, K. (2013). Aplicaciones del método de Monte Carlo en física estadística . Springer Science & Business Media. ISBN 978-3-642-51703-7.
14. Fröhlich, J.; Spencer, T. (1981). "La transición de Kosterlitz–Thouless en sistemas de espín abeliano bidimensionales y el gas de Coulomb". Communications in Mathematical Physics . 81 (4): 527–602. Bibcode :1981CMaPh..81..527F. doi :10.1007/bf01208273. S2CID  73555642.
15. Chester, Shai M.; Landry, Walter; Liu, Junyu; Poland, David; Simmons-Duffin, David; Su, Ning; Vichi, Alessandro (2020). "Extracción del espacio OPE y exponentes críticos del modelo O(2) preciso". Journal of High Energy Physics . 2020 (6): 142. arXiv : 1912.03324 . Código Bibliográfico :2020JHEP...06..142C. doi :10.1007/JHEP06(2020)142. ISSN  1029-8479. S2CID  208910721.
16. Hasenbusch, Martin (26 de diciembre de 2019). "Estudio de Monte Carlo de un modelo de reloj mejorado en tres dimensiones". Physical Review B . 100 (22): 224517. arXiv : 1910.05916 . Código Bibliográfico :2019PhRvB.100v4517H. doi :10.1103/PhysRevB.100.224517. ISSN  2469-9950. S2CID  204509042.

Referencias

• Evgeny Demidov, Vórtices en el modelo XY (2004)

Lectura adicional

• HE Stanley, Introducción a las transiciones de fase y fenómenos críticos , (Oxford University Press, Oxford y Nueva York 1971);
• H. Kleinert , Gauge Fields in Condensed Matter , Vol. I, "SUPERFLOW AND VORTEX LINES", págs. 1–742, Vol. II, "STRESSES AND DEFECTS", págs. 743–1456, World Scientific (Singapur, 1989); ISBN de tapa blanda 9971-5-0210-0 (también disponible en línea: Vol. I y Vol. II) 

Enlaces externos

• Simulación WebGL del modelo XY en tiempo real
• Simulación interactiva de Monte Carlo de los modelos Ising, XY y Heisenberg con gráficos 3D (requiere navegador compatible con WebGL)