Controlador proporcional-integral-derivativo

Mecanismo de retroalimentación del bucle de control

Un controlador proporcional-integral-derivativo ( controlador PID o controlador de tres términos ) es un mecanismo de control de bucle basado en retroalimentación que se utiliza habitualmente para gestionar máquinas y procesos que requieren un control continuo y un ajuste automático. Se utiliza normalmente en sistemas de control industrial y en otras aplicaciones en las que es necesario un control constante mediante modulación sin intervención humana. El controlador PID compara automáticamente el valor objetivo deseado ( punto de ajuste o SP) con el valor real del sistema ( variable de proceso o PV). La diferencia entre estos dos valores se denomina valor de error , denotado como . ${\displaystyle e(t)}$

Luego aplica acciones correctivas automáticamente para llevar el PV al mismo valor que el SP utilizando tres métodos: El componente proporcional ( P ) responde al valor de error actual produciendo una salida que es directamente proporcional a la magnitud del error. Esto proporciona una corrección inmediata basada en qué tan lejos está el sistema del punto de ajuste deseado. El componente integral ( I ), a su vez, considera la suma acumulada de errores pasados ​​para abordar cualquier error residual de estado estable que persista en el tiempo, eliminando discrepancias persistentes. Por último, el componente derivado ( D ) predice el error futuro evaluando la tasa de cambio del error, lo que ayuda a mitigar el sobreimpulso y mejorar la estabilidad del sistema, particularmente cuando el sistema experimenta cambios rápidos. El controlador PID reduce la probabilidad de error humano y mejora la automatización .

Un ejemplo común es el sistema de control de crucero de un vehículo . Cuando un vehículo se encuentra con una pendiente, su velocidad puede disminuir debido a la potencia constante del motor. El controlador PID ajusta la potencia de salida del motor para restaurar el vehículo a su velocidad deseada, haciéndolo de manera eficiente con un retraso y un exceso mínimos.

La base teórica de los controladores PID se remonta a principios de la década de 1920 con el desarrollo de sistemas de dirección automática para barcos. Este concepto se adoptó más tarde para el control automático de procesos en la fabricación, apareciendo primero en actuadores neumáticos y evolucionando hacia controladores electrónicos. Los controladores PID se utilizan ampliamente en numerosas aplicaciones que requieren un control automático preciso, estable y optimizado , como la regulación de temperatura , el control de velocidad del motor y la gestión de procesos industriales.

Operación fundamental

Diagrama de bloques de un controlador PID en un bucle de retroalimentación. r ( t ) es la variable de proceso deseada (PV) o punto de ajuste (SP), e y ( t ) es el PV medido.

La característica distintiva del controlador PID es la capacidad de utilizar los tres términos de control de influencia proporcional, integral y derivativa en la salida del controlador para aplicar un control preciso y óptimo. El diagrama de bloques de la derecha muestra los principios de cómo se generan y aplican estos términos. Muestra un controlador PID, que calcula continuamente un valor de error como la diferencia entre un punto de ajuste deseado y una variable de proceso medida : , y aplica una corrección basada en términos proporcionales , integrales y derivativos . El controlador intenta minimizar el error a lo largo del tiempo mediante el ajuste de una variable de control , como la apertura de una válvula de control , a un nuevo valor determinado por una suma ponderada de los términos de control. ${\displaystyle e(t)}$ ${\displaystyle {\text{SP}}=r(t)}$ ${\displaystyle {\text{PV}}=y(t)}$ ${\displaystyle e(t)=r(t)-y(t)}$ ${\displaystyle u(t)}$

En este modelo:

• El término P es proporcional al valor actual del error SP − PV . Por ejemplo, si el error es grande, la salida de control será proporcionalmente grande utilizando el factor de ganancia "K _p ". El uso del control proporcional únicamente dará como resultado un error entre el punto de ajuste y el valor del proceso porque el controlador requiere un error para generar la respuesta de salida proporcional. En condiciones de proceso de estado estable, se alcanza un equilibrio, con un "desfase" SP-PV estable. ${\displaystyle e(t)}$
• El término I tiene en cuenta los valores pasados ​​del error SP − PV y los integra a lo largo del tiempo para producir el término I. Por ejemplo, si hay un error SP − PV residual después de la aplicación del control proporcional, el término integral busca eliminar el error residual añadiendo un efecto de control debido al valor acumulado histórico del error. Cuando se elimina el error, el término integral dejará de crecer. Esto hará que el efecto proporcional disminuya a medida que disminuye el error, pero esto se compensa con el efecto integral creciente.
• El término D es una mejor estimación de la tendencia futura del error SP − PV, basada en su tasa actual de cambio. A veces se lo denomina "control anticipatorio", ya que busca reducir efectivamente el efecto del error SP − PV al ejercer una influencia de control generada por la tasa de cambio del error. Cuanto más rápido sea el cambio, mayor será el efecto de control o amortiguación. ^[1]

Ajuste : el equilibrio de estos efectos se logra mediante el ajuste de bucle para producir la función de control óptima. Las constantes de ajuste se muestran a continuación como "K" y deben derivarse para cada aplicación de control, ya que dependen de las características de respuesta del sistema físico, externo al controlador. Estas dependen del comportamiento del sensor de medición, el elemento de control final (como una válvula de control), cualquier retraso de la señal de control y el proceso en sí. Por lo general, se pueden ingresar valores aproximados de las constantes inicialmente conociendo el tipo de aplicación, pero normalmente se refinan o ajustan introduciendo un cambio de punto de ajuste y observando la respuesta del sistema. ^[2]

Acción de control : tanto el modelo matemático como el bucle práctico anteriores utilizan una acción de control directa para todos los términos, lo que significa que un error positivo creciente da como resultado una corrección positiva creciente de la salida de control. Esto se debe a que el término "error" no es la desviación del punto de ajuste (real-deseado) sino que es, de hecho, la corrección necesaria (deseado-real). El sistema se denomina de acción inversa si es necesario aplicar una acción correctiva negativa. Por ejemplo, si la válvula en el bucle de flujo tenía una apertura de válvula del 100-0 % para una salida de control del 0-100 %, lo que significa que la acción del controlador debe invertirse. Algunos esquemas de control de procesos y elementos de control final requieren esta acción inversa. Un ejemplo sería una válvula para agua de refrigeración, donde el modo a prueba de fallos , en el caso de pérdida de señal, sería una apertura del 100 % de la válvula; por lo tanto, una salida del controlador del 0 % debe provocar una apertura de la válvula del 100 %.

Forma matemática

La función de control general ${\displaystyle u(t)=K_{\text{p}}e(t)+K_{\text{i}}\int _{0}^{t}e(\tau )\,\mathrm {d} \tau +K_{\text{d}}{\frac {\mathrm {d} e(t)}{\mathrm {d} t}},}$

donde , , y , todos no negativos, denotan los coeficientes para los términos proporcional, integral y derivado respectivamente (a veces denotados P , I y D ). ${\displaystyle K_{\text{p}}}$ ${\displaystyle K_{\text{i}}}$ ${\displaystyle K_{\text{d}}}$

En la forma estándar de la ecuación (ver más adelante en el artículo), y se reemplazan respectivamente por y ; la ventaja de esto es que y tienen un significado físico comprensible, ya que representan un tiempo de integración y un tiempo de derivada respectivamente. es la constante de tiempo con la que el controlador intentará aproximarse al punto establecido. determina cuánto tiempo tolerará el controlador que la salida esté constantemente por encima o por debajo del punto establecido. ${\displaystyle K_{\text{i}}}$ ${\displaystyle K_{\text{d}}}$ ${\displaystyle K_{\text{p}}/T_{\text{i}}}$ ${\displaystyle K_{\text{p}}T_{\text{d}}}$ ${\displaystyle T_{\text{i}}}$ ${\displaystyle T_{\text{d}}}$ ${\displaystyle K_{\text{p}}T_{\text{d}}}$ ${\displaystyle K_{\text{p}}/T_{\text{i}}}$

${\displaystyle u(t)=K_{\text{p}}\left(e(t)+{\frac {1}{T_{\text{i}}}}\int _{0}^{t}e(\tau )\,\mathrm {d} \tau +T_{\text{d}}{\frac {\mathrm {d} e(t)}{\mathrm {d} t}}\right)}$

Uso selectivo de términos de control

Aunque un controlador PID tiene tres términos de control, algunas aplicaciones necesitan solo uno o dos términos para proporcionar un control adecuado. Esto se logra estableciendo los parámetros no utilizados en cero y se denomina controlador PI, PD, P o I en ausencia de las otras acciones de control. Los controladores PI son bastante comunes en aplicaciones donde la acción derivativa sería sensible al ruido de medición, pero el término integral a menudo es necesario para que el sistema alcance su valor objetivo. ^{[ cita requerida ]}

Aplicabilidad

El uso del algoritmo PID no garantiza un control óptimo del sistema ni su estabilidad de control ( ver § Limitaciones, a continuación ). Pueden darse situaciones en las que haya demoras excesivas: la medición del valor del proceso se retrasa o la acción de control no se aplica con la suficiente rapidez. En estos casos, se requiere una compensación de adelanto-retraso para que sea efectiva. La respuesta del controlador se puede describir en términos de su capacidad de respuesta a un error, el grado en el que el sistema sobrepasa un punto de ajuste y el grado de cualquier oscilación del sistema . Pero el controlador PID es ampliamente aplicable ya que se basa solo en la respuesta de la variable de proceso medida, no en el conocimiento o un modelo del proceso subyacente.

Historia

La primera teoría PID se desarrolló observando las acciones de los timoneles al mantener el rumbo de un barco frente a influencias variables como el viento y el estado del mar.

Controlador neumático PID (de tres términos). Las magnitudes de los tres términos (P, I y D) se ajustan mediante los diales de la parte superior.

Orígenes

El control continuo, antes de que los controladores PID fueran completamente comprendidos e implementados, tiene uno de sus orígenes en el regulador centrífugo , que utiliza pesos rotatorios para controlar un proceso. Este fue inventado por Christiaan Huygens en el siglo XVII para regular la distancia entre las muelas de los molinos de viento en función de la velocidad de rotación, y compensar así la velocidad variable de alimentación del grano. ^{[3] [4]}

Con la invención de la máquina de vapor estacionaria de baja presión surgió la necesidad de un control automático de la velocidad, y el regulador de " péndulo cónico " diseñado por el propio James Watt , un conjunto de bolas de acero giratorias unidas a un husillo vertical mediante brazos articulados, se convirtió en un estándar de la industria. Este se basaba en el concepto de control de la distancia entre las muelas del molino. ^[5]

Sin embargo, el control de velocidad mediante regulador rotatorio seguía siendo variable en condiciones de carga variable, donde era evidente la deficiencia de lo que ahora se conoce como control proporcional por sí solo. El error entre la velocidad deseada y la velocidad real aumentaría con el aumento de la carga. En el siglo XIX, la base teórica para el funcionamiento de los reguladores fue descrita por primera vez por James Clerk Maxwell en 1868 en su ahora famoso artículo On Governors . Exploró la base matemática para la estabilidad del control y avanzó un buen camino hacia una solución, pero hizo un llamamiento a los matemáticos para que examinaran el problema. ^{[6] [5]} El problema fue examinado más a fondo en 1874 por Edward Routh , Charles Sturm y, en 1895, Adolf Hurwitz , todos ellos contribuyeron al establecimiento de criterios de estabilidad del control. ^[5] En aplicaciones posteriores, los reguladores de velocidad se refinaron aún más, en particular por el científico estadounidense Willard Gibbs , quien en 1872 analizó teóricamente el regulador de péndulo cónico de Watt.

En esa época, la invención del torpedo Whitehead planteó un problema de control que requería un control preciso de la profundidad de carrera. El uso de un sensor de presión de profundidad por sí solo resultó inadecuado, y un péndulo que medía el cabeceo de proa y popa del torpedo se combinó con la medición de profundidad para convertirse en el control de péndulo e hidrostato . El control de presión proporcionaba solo un control proporcional que, si la ganancia de control era demasiado alta, se volvería inestable y entraría en sobreimpulso con una inestabilidad considerable en el mantenimiento de la profundidad. El péndulo agregó lo que ahora se conoce como control derivativo, que amortiguaba las oscilaciones detectando el ángulo de inmersión/ascenso del torpedo y, por lo tanto, la tasa de cambio de profundidad. ^[7] Este desarrollo (nombrado por Whitehead como "El Secreto" para no dar ninguna pista sobre su acción) fue alrededor de 1868. ^[8]

Otro ejemplo temprano de un controlador de tipo PID fue desarrollado por Elmer Sperry en 1911 para la dirección de barcos, aunque su trabajo era intuitivo en lugar de estar basado en matemáticas. ^[9]

Sin embargo, no fue hasta 1922 que el ingeniero ruso-estadounidense Nicolas Minorsky desarrolló por primera vez una ley de control formal para lo que ahora llamamos PID o control de tres términos utilizando análisis teórico . ^[10] Minorsky estaba investigando y diseñando la dirección automática de barcos para la Marina de los EE. UU. y basó su análisis en las observaciones de un timonel . Observó que el timonel dirigía el barco basándose no solo en el error de rumbo actual sino también en el error pasado, así como en la tasa de cambio actual; ^[11] Minorsky luego le dio un tratamiento matemático a esto. ^[5] Su objetivo era la estabilidad, no el control general, lo que simplificó significativamente el problema. Si bien el control proporcional brindaba estabilidad frente a pequeñas perturbaciones, era insuficiente para lidiar con una perturbación constante, en particular un vendaval fuerte (debido al error de estado estable), que requería agregar el término integral. Finalmente, se agregó el término derivativo para mejorar la estabilidad y el control.

Se realizaron pruebas en el USS New Mexico , con los controladores controlando la velocidad angular (no el ángulo) del timón. El control PI produjo un guiñada sostenida (error angular) de ±2°. La adición del elemento D produjo un error de guiñada de ±1/6°, mejor de lo que la mayoría de los timoneles podrían lograr. ^[12]

La Marina finalmente no adoptó el sistema debido a la resistencia del personal. Varios otros realizaron y publicaron trabajos similares ^{[ ¿quiénes? ]} en la década de 1930. ^{[ cita requerida ]}

Control industrial

Control proporcional mediante amplificador de alta ganancia de boquilla y aleta y retroalimentación negativa

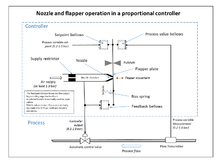
El uso generalizado de controladores de retroalimentación no se hizo factible hasta el desarrollo de amplificadores de banda ancha de alta ganancia para utilizar el concepto de retroalimentación negativa . Esto había sido desarrollado en electrónica de ingeniería telefónica por Harold Black a fines de la década de 1920, pero no publicado hasta 1934. ^[5] Independientemente, Clesson E Mason de Foxboro Company en 1930 inventó un controlador neumático de banda ancha combinando el amplificador neumático de alta ganancia de boquilla y aleta , que se había inventado en 1914, con retroalimentación negativa de la salida del controlador. Esto aumentó drásticamente el rango lineal de operación del amplificador de boquilla y aleta, y también se pudo agregar control integral mediante el uso de una válvula de purga de precisión y un fuelle que genera el término integral. El resultado fue el controlador "Stabilog" que proporcionó funciones proporcionales e integrales utilizando fuelles de retroalimentación. ^[5] El término integral se llamó Reset . ^[13] Más tarde, se agregó el término derivativo mediante un fuelle adicional y un orificio ajustable.

A partir de 1932, aproximadamente, el uso de controladores neumáticos de banda ancha aumentó rápidamente en una variedad de aplicaciones de control. La presión del aire se utilizaba para generar la salida del controlador y también para alimentar dispositivos de modulación de procesos, como válvulas de control operadas por diafragma. Eran dispositivos simples que requerían poco mantenimiento y funcionaban bien en entornos industriales hostiles y no presentaban riesgos de explosión en lugares peligrosos . Fueron el estándar de la industria durante muchas décadas hasta la llegada de los controladores electrónicos discretos y los sistemas de control distribuido (DCS).

Con estos controladores, se estableció un estándar de señalización de la industria neumática de 3 a 15 psi (0,2 a 1,0 bar), que tenía un cero elevado para garantizar que los dispositivos funcionaran dentro de su característica lineal y representara el rango de control de 0 a 100 %.

En la década de 1950, cuando los amplificadores electrónicos de alta ganancia se volvieron baratos y confiables, los controladores electrónicos PID se hicieron populares y el estándar neumático fue emulado por señales de bucle de corriente de 10-50 mA y 4-20 mA (esta última se convirtió en el estándar de la industria). Los actuadores de campo neumáticos todavía se usan ampliamente debido a las ventajas de la energía neumática para las válvulas de control en entornos de plantas de proceso.

Se muestra la evolución de la señalización del lazo de control analógico desde la era neumática hasta la electrónica.

Se muestran los bucles de corriente utilizados para detectar y controlar señales. Se muestra un posicionador de válvula electrónico "inteligente" moderno, que incorporará su propio controlador PID.

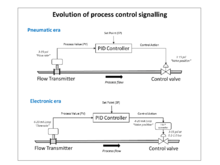
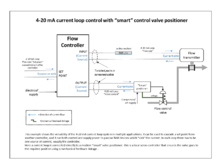
La mayoría de los controles PID modernos en la industria se implementan como software de computadora en DCS, controladores lógicos programables (PLC) o controladores compactos discretos .

Controladores analógicos electrónicos

Los bucles de control PID analógicos electrónicos se encontraban a menudo dentro de sistemas electrónicos más complejos, por ejemplo, el posicionamiento del cabezal de una unidad de disco , el acondicionamiento de energía de una fuente de alimentación o incluso el circuito de detección de movimiento de un sismómetro moderno . Los controladores analógicos electrónicos discretos han sido reemplazados en gran medida por controladores digitales que utilizan microcontroladores o FPGA para implementar algoritmos PID. Sin embargo, los controladores PID analógicos discretos todavía se utilizan en aplicaciones de nicho que requieren un alto ancho de banda y un rendimiento de bajo ruido, como los controladores de diodos láser. ^[14]

Ejemplo de bucle de control

Consideremos un brazo robótico ^[15] que se puede mover y posicionar mediante un bucle de control. Un motor eléctrico puede levantar o bajar el brazo, dependiendo de la potencia aplicada hacia adelante o hacia atrás, pero la potencia no puede ser una función simple de la posición debido a la masa inercial del brazo, las fuerzas debidas a la gravedad, las fuerzas externas sobre el brazo, como una carga para levantar o el trabajo que se debe realizar sobre un objeto externo.

• La posición detectada es la variable del proceso (PV).
• La posición deseada se llama punto de ajuste (SP).
• La diferencia entre el PV y el SP es el error (e), que cuantifica si el brazo está demasiado bajo o demasiado alto y en qué medida.
• La entrada al proceso (la corriente eléctrica en el motor) es la salida del controlador PID. Se denomina variable manipulada (MV) o variable de control (CV).

Midiendo la posición (PV) y restándola del punto de ajuste (SP), se encuentra el error (e), y a partir de él el controlador calcula cuánta corriente eléctrica debe suministrar al motor (MV).

Proporcional

El método obvio es el control proporcional : la corriente del motor se ajusta en proporción al error existente. Sin embargo, este método falla si, por ejemplo, el brazo tiene que levantar pesos diferentes: un peso mayor requiere una fuerza mayor aplicada para el mismo error en el lado descendente, pero una fuerza menor si el error es bajo en el lado ascendente. Ahí es donde los términos integrales y derivativos juegan su papel.

Integral

Un término integral aumenta la acción en relación no sólo con el error sino también con el tiempo durante el cual ha persistido. Por lo tanto, si la fuerza aplicada no es suficiente para llevar el error a cero, esta fuerza se incrementará a medida que transcurra el tiempo. Un controlador "yo" puro podría llevar el error a cero, pero reaccionaría débilmente al principio (porque la acción sería pequeña al principio, dependiendo del tiempo para volverse significativa) y más agresiva al final (la acción aumenta mientras el error sea positivo, incluso si el error es cercano a cero).

La aplicación de una integral excesiva cuando el error es pequeño y decreciente dará lugar a un sobreimpulso. Después del sobreimpulso, si el controlador aplicara una corrección grande en la dirección opuesta y sobrepasara repetidamente la posición deseada, la salida oscilaría alrededor del punto de ajuste en una sinusoide constante, creciente o decreciente . Si la amplitud de las oscilaciones aumenta con el tiempo, el sistema es inestable. Si disminuye, el sistema es estable. Si las oscilaciones permanecen en una magnitud constante, el sistema es marginalmente estable .

Derivado

Un término derivado no considera la magnitud del error (es decir, no puede reducirlo a cero: un controlador D puro no puede llevar el sistema a su punto de ajuste), sino la tasa de cambio del error, tratando de llevar esta tasa a cero. Su objetivo es aplanar la trayectoria del error en una línea horizontal, amortiguando la fuerza aplicada y, por lo tanto, reduciendo el sobreimpulso (error en el otro lado debido a una fuerza aplicada demasiado grande).

Control de amortiguación

Para lograr una llegada controlada a la posición deseada (SP) de manera oportuna y precisa, el sistema controlado debe estar amortiguado críticamente . Un sistema de control de posición bien ajustado también aplicará las corrientes necesarias al motor controlado para que el brazo empuje y tire según sea necesario para resistir las fuerzas externas que intentan alejarlo de la posición requerida. El punto de ajuste en sí puede ser generado por un sistema externo, como un PLC u otro sistema informático, de modo que varíe continuamente según el trabajo que se espera que realice el brazo robótico. Un sistema de control PID bien ajustado permitirá que el brazo cumpla con estos requisitos cambiantes al máximo de sus capacidades.

Respuesta a las perturbaciones

Si un controlador comienza desde un estado estable con error cero (PV = SP), los cambios posteriores que realice el controlador se harán en respuesta a cambios en otras entradas medidas o no medidas del proceso que afecten al proceso y, por lo tanto, al PV. Las variables que afectan al proceso además de la MV se conocen como perturbaciones. Generalmente, los controladores se utilizan para rechazar perturbaciones e implementar cambios en los puntos de ajuste. Un cambio en la carga del brazo constituye una perturbación en el proceso de control del brazo robótico.

Aplicaciones

En teoría, un controlador se puede utilizar para controlar cualquier proceso que tenga una salida medible (PV), un valor ideal conocido para esa salida (SP) y una entrada al proceso (MV) que afectará la PV relevante. Los controladores se utilizan en la industria para regular la temperatura , la presión , la fuerza , la velocidad de alimentación , ^[16] el caudal , la composición química ( concentraciones de componentes ), el peso , la posición , la velocidad y prácticamente cualquier otra variable para la que exista una medición.

Teoría del controlador

En esta sección se describe la forma paralela o no interactiva del controlador PID. Para otras formas, consulte § Nomenclatura y formas alternativas.

El esquema de control PID recibe su nombre de sus tres términos correctores, cuya suma constituye la variable manipulada (MV). Los términos proporcional, integral y derivativo se suman para calcular la salida del controlador PID. Definida como la salida del controlador, la forma final del algoritmo PID es ${\displaystyle u(t)}$

${\displaystyle u(t)=\mathrm {MV} (t)=K_{\text{p}}e(t)+K_{\text{i}}\int _{0}^{t}e(\tau )\,d\tau +K_{\text{d}}{\frac {de(t)}{dt}},}$

dónde

${\displaystyle K_{\text{p}}}$es la ganancia proporcional, un parámetro de ajuste,

${\displaystyle K_{\text{i}}}$es la ganancia integral, un parámetro de ajuste,

${\displaystyle K_{\text{d}}}$es la ganancia derivada, un parámetro de ajuste,

${\displaystyle e(t)=\mathrm {SP} -\mathrm {PV} (t)}$es el error (SP es el punto de ajuste y PV( t ) es la variable del proceso),

${\displaystyle t}$es el tiempo o tiempo instantáneo (el presente),

${\displaystyle \tau }$es la variable de integración (toma valores desde el tiempo 0 hasta el presente ). ${\displaystyle t}$

De manera equivalente, la función de transferencia en el dominio de Laplace del controlador PID es

${\displaystyle L(s)=K_{\text{p}}+K_{\text{i}}/s+K_{\text{d}}s,}$

¿Dónde está la frecuencia compleja? ${\displaystyle s}$

Término proporcional

Respuesta de PV a un cambio escalonado de SP en función del tiempo, para tres valores de K _p ( K _i y K _d se mantienen constantes)

El término proporcional produce un valor de salida que es proporcional al valor de error actual. La respuesta proporcional se puede ajustar multiplicando el error por una constante K _p , denominada constante de ganancia proporcional.

El término proporcional viene dado por

${\displaystyle P_{\text{out}}=K_{\text{p}}e(t).}$

Una ganancia proporcional alta da como resultado un gran cambio en la salida para un cambio dado en el error. Si la ganancia proporcional es demasiado alta, el sistema puede volverse inestable (consulte la sección sobre ajuste de bucle). Por el contrario, una ganancia pequeña da como resultado una respuesta de salida pequeña a un gran error de entrada y un controlador menos sensible o con menor capacidad de respuesta. Si la ganancia proporcional es demasiado baja, la acción de control puede ser demasiado pequeña al responder a las perturbaciones del sistema. La teoría del ajuste y la práctica industrial indican que el término proporcional debería contribuir con la mayor parte del cambio de salida. ^{[ cita requerida ]}

Error de estado estable

El error de estado estable es la diferencia entre la salida final deseada y la real. ^[17] Debido a que se requiere un error distinto de cero para impulsarlo, un controlador proporcional generalmente opera con un error de estado estable. ^[a] El error de estado estable (SSE) es proporcional a la ganancia del proceso e inversamente proporcional a la ganancia proporcional. El SSE se puede mitigar agregando un término de polarización de compensación al punto de ajuste Y la salida o se puede corregir dinámicamente agregando un término integral.

Término integral

Respuesta de PV a un cambio escalonado de SP en función del tiempo, para tres valores de K _i ( K _p y K _d se mantienen constantes)

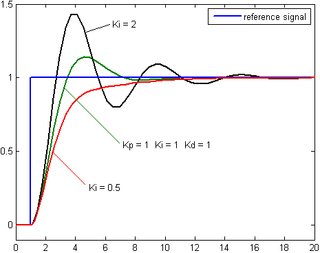
La contribución del término integral es proporcional tanto a la magnitud del error como a su duración. En un controlador PID, la integral es la suma del error instantáneo a lo largo del tiempo y proporciona el desfase acumulado que debería haberse corregido previamente. El error acumulado se multiplica luego por la ganancia integral ( K _i ) y se suma a la salida del controlador.

El término integral viene dado por

${\displaystyle I_{\text{out}}=K_{\text{i}}\int _{0}^{t}e(\tau )\,d\tau .}$

El término integral acelera el movimiento del proceso hacia el punto de ajuste y elimina el error residual de estado estable que se produce con un controlador proporcional puro. Sin embargo, dado que el término integral responde a errores acumulados del pasado, puede provocar que el valor actual supere el valor del punto de ajuste (consulte la sección sobre ajuste de bucle).

Término derivado

Respuesta de PV a un cambio escalonado de SP en función del tiempo, para tres valores de K _d ( K _p y K _i se mantienen constantes)

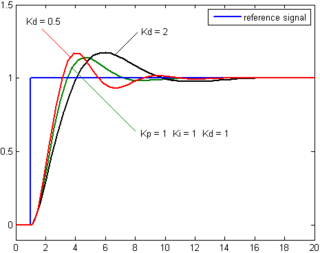
La derivada del error de proceso se calcula determinando la pendiente del error a lo largo del tiempo y multiplicando esta tasa de cambio por la ganancia de la derivada K _d . La magnitud de la contribución del término de la derivada a la acción de control general se denomina ganancia de la derivada, K _d .

El término derivado viene dado por

${\displaystyle D_{\text{out}}=K_{\text{d}}{\frac {de(t)}{dt}}.}$

La acción derivada predice el comportamiento del sistema y, por lo tanto, mejora el tiempo de asentamiento y la estabilidad del sistema. ^{[18] [19]} Una derivada ideal no es causal , por lo que las implementaciones de controladores PID incluyen un filtrado de paso bajo adicional para el término derivado para limitar la ganancia de alta frecuencia y el ruido. Sin embargo, la acción derivada rara vez se usa en la práctica (según una estimación, solo en el 25 % de los controladores implementados ^{[ cita requerida ]} ) debido a su impacto variable en la estabilidad del sistema en aplicaciones del mundo real.

Sintonización de bucle

Ajustar un lazo de control es ajustar sus parámetros de control (ganancia/banda proporcional, ganancia/reinicio integral, tasa/ganancia derivativa) a los valores óptimos para la respuesta de control deseada. La estabilidad (sin oscilaciones ilimitadas) es un requisito básico, pero más allá de eso, los diferentes sistemas tienen comportamientos diferentes, las diferentes aplicaciones tienen requisitos diferentes y los requisitos pueden entrar en conflicto entre sí.

Aunque sólo hay tres parámetros y es sencillo de describir en principio, el ajuste PID es un problema difícil porque debe satisfacer criterios complejos dentro de las limitaciones del control PID. En consecuencia, existen varios métodos para el ajuste de bucles, y las técnicas más sofisticadas son objeto de patentes; en esta sección se describen algunos métodos manuales tradicionales para el ajuste de bucles.

El diseño y ajuste de un controlador PID parece ser conceptualmente intuitivo, pero puede ser difícil en la práctica si se deben lograr objetivos múltiples (y a menudo contradictorios), como transitorios cortos y alta estabilidad. Los controladores PID a menudo brindan un control aceptable utilizando ajustes predeterminados, pero el rendimiento generalmente se puede mejorar con un ajuste cuidadoso, y el rendimiento puede ser inaceptable con un ajuste deficiente. Por lo general, los diseños iniciales deben ajustarse repetidamente mediante simulaciones por computadora hasta que el sistema de bucle cerrado funcione o se comprometa según lo deseado.

Algunos procesos tienen un grado de no linealidad , por lo que los parámetros que funcionan bien en condiciones de carga completa no funcionan cuando el proceso se inicia sin carga. Esto se puede corregir mediante la programación de la ganancia (utilizando diferentes parámetros en diferentes regiones operativas).

Estabilidad

Si los parámetros del controlador PID (las ganancias de los términos proporcional, integral y derivativo) se eligen incorrectamente, la entrada del proceso controlado puede ser inestable; es decir, su salida diverge , con o sin oscilación , y está limitada únicamente por la saturación o la rotura mecánica. La inestabilidad es causada por el exceso de ganancia, particularmente en presencia de un desfase significativo.

Generalmente, se requiere la estabilización de la respuesta y el proceso no debe oscilar para ninguna combinación de condiciones de proceso y puntos de ajuste, aunque a veces la estabilidad marginal (oscilación limitada) es aceptable o deseada. ^{[ cita requerida ]}

Matemáticamente, los orígenes de la inestabilidad se pueden ver en el dominio de Laplace . ^[20]

La función de transferencia de bucle cerrado es

${\displaystyle H(s)={\frac {K(s)G(s)}{1+K(s)G(s)}},}$

donde es la función de transferencia PID, y es la función de transferencia de la planta. Un sistema es inestable cuando la función de transferencia de lazo cerrado diverge para algún . ^[20] Esto sucede en situaciones donde . En otras palabras, esto sucede cuando con un cambio de fase de 180°. La estabilidad está garantizada cuando para frecuencias que sufren grandes cambios de fase. Un formalismo más general de este efecto se conoce como el criterio de estabilidad de Nyquist . ${\displaystyle K(s)}$ ${\displaystyle G(s)}$ ${\displaystyle s}$ ${\displaystyle K(s)G(s)=-1}$ ${\displaystyle |K(s)G(s)|=1}$ ${\displaystyle K(s)G(s)<1}$

Comportamiento óptimo

El comportamiento óptimo ante un cambio de proceso o de punto de ajuste varía según la aplicación.

Dos requisitos básicos son la regulación (rechazo de perturbaciones, permanencia en un punto de ajuste determinado) y el seguimiento de comandos (implementación de cambios en el punto de ajuste). Estos términos se refieren a qué tan bien la variable controlada sigue el valor deseado. Los criterios específicos para el seguimiento de comandos incluyen el tiempo de subida y el tiempo de estabilización . Algunos procesos no deben permitir un sobreimpulso de la variable de proceso más allá del punto de ajuste si, por ejemplo, esto sería inseguro. Otros procesos deben minimizar la energía gastada para alcanzar un nuevo punto de ajuste.

Descripción general de los métodos de ajuste

Existen varios métodos para ajustar un bucle PID. Los métodos más eficaces generalmente implican el desarrollo de algún tipo de modelo de proceso y luego la elección de P, I y D en función de los parámetros del modelo dinámico. Los métodos de ajuste manual pueden requerir bastante tiempo, en particular para sistemas con tiempos de bucle prolongados.

La elección del método depende en gran medida de si el bucle se puede desconectar para realizar el ajuste y del tiempo de respuesta del sistema. Si el sistema se puede desconectar, el mejor método de ajuste suele implicar someter al sistema a un cambio escalonado en la entrada, medir la salida en función del tiempo y utilizar esta respuesta para determinar los parámetros de control. ^{[ cita requerida ]}

Sintonización manual

Si el sistema debe permanecer en línea, un método de ajuste consiste en establecer primero los valores y en cero. Aumente hasta que la salida del bucle oscile; luego, ajústelo a aproximadamente la mitad de ese valor para una respuesta de tipo "caída de amplitud de un cuarto". Luego, aumente hasta que cualquier desviación se corrija con tiempo suficiente para el proceso, pero no hasta que un valor demasiado grande provoque inestabilidad. Finalmente, aumente , si es necesario, hasta que el bucle alcance su referencia con una velocidad aceptable después de una perturbación de carga. Un valor demasiado alto provoca una respuesta excesiva y un sobreimpulso. Un ajuste rápido del bucle PID generalmente sobreimpulsa ligeramente para alcanzar el punto de ajuste más rápidamente; sin embargo, algunos sistemas no pueden aceptar el sobreimpulso, en cuyo caso se requiere un sistema de bucle cerrado sobreamortiguado , que a su vez requiere un ajuste significativamente menor que la mitad del ajuste que estaba causando la oscilación. ^{[ cita requerida ]} ${\displaystyle K_{i}}$ ${\displaystyle K_{d}}$ ${\displaystyle K_{p}}$ ${\displaystyle K_{p}}$ ${\displaystyle K_{i}}$ ${\displaystyle K_{d}}$ ${\displaystyle K_{p}}$ ${\displaystyle K_{p}}$ ${\displaystyle K_{p}}$

Efectos de la variación de los parámetros PID (K _p ,K _i ,K _d ) en la respuesta al escalón de un sistema

Método Ziegler-Nichols

Otro método de ajuste heurístico es el conocido como método Ziegler-Nichols , introducido por John G. Ziegler y Nathaniel B. Nichols en la década de 1940. Al igual que en el método anterior, las ganancias y se establecen primero en cero. La ganancia proporcional se aumenta hasta que alcanza la ganancia máxima en la que la salida del bucle comienza a oscilar constantemente. y el período de oscilación se utilizan para establecer las ganancias de la siguiente manera: ${\displaystyle K_{i}}$ ${\displaystyle K_{d}}$ ${\displaystyle K_{u}}$ ${\displaystyle K_{u}}$ ${\displaystyle T_{u}}$

A menudo se mide la frecuencia de oscilación y los recíprocos de cada multiplicación dan el mismo resultado.

Estas ganancias se aplican a la forma ideal y paralela del controlador PID. Cuando se aplican a la forma PID estándar, solo las ganancias integral y derivativa dependen del período de oscilación . ${\displaystyle K_{i}}$ ${\displaystyle K_{d}}$ ${\displaystyle T_{u}}$

Parámetros de Cohen-Coon

Este método se desarrolló en 1953 y se basa en un modelo de primer orden + retardo temporal. De manera similar al método Ziegler-Nichols , se desarrolló un conjunto de parámetros de ajuste para producir una respuesta de bucle cerrado con una relación de decaimiento de . Se podría decir que el mayor problema con estos parámetros es que un pequeño cambio en los parámetros del proceso podría hacer que un sistema de bucle cerrado se volviera inestable. ${\displaystyle {\tfrac {1}{4}}}$

Método de relevo (Åström-Hägglund)

Publicado en 1984 por Karl Johan Åström y Tore Hägglund, ^[25] el método del relé opera temporalmente el proceso usando control bang-bang y mide las oscilaciones resultantes. La salida se conmuta (como si fuera un relé , de ahí el nombre) entre dos valores de la variable de control. Los valores deben elegirse de manera que el proceso cruce el punto de ajuste, pero no es necesario que sean 0% y 100%; al elegir valores adecuados, se pueden evitar oscilaciones peligrosas.

Mientras la variable de proceso se encuentre por debajo del punto de ajuste, la salida de control se establece en el valor más alto. Tan pronto como se eleve por encima del punto de ajuste, la salida de control se establece en el valor más bajo. Idealmente, la forma de onda de salida es casi cuadrada, y pasa el mismo tiempo por encima y por debajo del punto de ajuste. El período y la amplitud de las oscilaciones resultantes se miden y se utilizan para calcular la ganancia y el período finales, que luego se introducen en el método Ziegler-Nichols.

Específicamente, se supone que el período último es igual al período observado, y la ganancia última se calcula como donde a es la amplitud de la oscilación de la variable del proceso y b es la amplitud del cambio de salida de control que la causó. ${\displaystyle T_{u}}$ ${\displaystyle K_{u}=4b/\pi a,}$

Existen numerosas variantes del método de relevo. ^[26]

Modelo de primer orden con tiempo muerto

La función de transferencia para un proceso de primer orden con tiempo muerto es

${\displaystyle y(s)={\frac {k_{\text{p}}e^{-\theta s}}{\tau _{\text{p}}s+1}}u(s),}$

donde k _p es la ganancia del proceso, τ _p es la constante de tiempo, θ es el tiempo muerto y u ( s ) es una entrada de cambio de paso. La conversión de esta función de transferencia al dominio del tiempo da como resultado

${\displaystyle y(t)=k_{\text{p}}\Delta u\left(1-e^{\frac {-t-\theta }{\tau _{\text{p}}}}\right),}$

utilizando los mismos parámetros encontrados anteriormente.

Al utilizar este método, es importante aplicar un cambio de paso de entrada lo suficientemente grande como para que se pueda medir la salida; sin embargo, un cambio de paso demasiado grande puede afectar la estabilidad del proceso. Además, un cambio de paso más grande garantiza que la salida no cambie debido a una perturbación (para obtener mejores resultados, intente minimizar las perturbaciones al realizar la prueba de pasos).

Una forma de determinar los parámetros para el proceso de primer orden es utilizando el método del 63,2%. En este método, la ganancia del proceso ( k _p ) es igual al cambio en la salida dividido por el cambio en la entrada. El tiempo muerto θ es la cantidad de tiempo entre cuando se produjo el cambio de paso y cuando la salida cambió por primera vez. La constante de tiempo ( τ _p ) es la cantidad de tiempo que tarda la salida en alcanzar el 63,2% del nuevo valor de estado estable después del cambio de paso. Una desventaja de utilizar este método es que puede llevar un tiempo alcanzar un nuevo valor de estado estable si el proceso tiene constantes de tiempo grandes. ^[27]

Software de ajuste

La mayoría de las instalaciones industriales modernas ya no ajustan los bucles mediante los métodos de cálculo manual que se muestran arriba. En su lugar, se utilizan software de optimización de bucles y ajuste PID para garantizar resultados consistentes. Estos paquetes de software recopilan datos, desarrollan modelos de procesos y sugieren un ajuste óptimo. Algunos paquetes de software pueden incluso desarrollar el ajuste mediante la recopilación de datos de los cambios de referencia.

El ajuste matemático del lazo PID induce un impulso en el sistema y luego utiliza la respuesta de frecuencia del sistema controlado para diseñar los valores del lazo PID. En lazos con tiempos de respuesta de varios minutos, se recomienda el ajuste matemático del lazo, porque el proceso de prueba y error puede llevar días solo para encontrar un conjunto estable de valores del lazo. Los valores óptimos son más difíciles de encontrar. Algunos controladores de lazo digital ofrecen una función de autoajuste en la que se envían cambios muy pequeños en el punto de ajuste al proceso, lo que permite que el propio controlador calcule los valores de ajuste óptimos.

Otro enfoque calcula valores iniciales a través del método Ziegler-Nichols y utiliza una técnica de optimización numérica para encontrar mejores coeficientes PID. ^[28]

Existen otras fórmulas disponibles para ajustar el circuito según diferentes criterios de rendimiento. Actualmente, muchas fórmulas patentadas están integradas en los módulos de hardware y software de ajuste de PID. ^[29]

Los avances en el software de ajuste automático de bucles PID también ofrecen algoritmos para ajustar bucles PID en un escenario dinámico o de estado no estacionario (NSS). El software modela la dinámica de un proceso, a través de una perturbación, y calcula los parámetros de control PID en respuesta. ^[30]

Limitaciones

Si bien los controladores PID son aplicables a muchos problemas de control y, a menudo, funcionan satisfactoriamente sin ninguna mejora o solo con un ajuste aproximado, pueden funcionar mal en algunas aplicaciones y, en general, no brindan un control óptimo . La dificultad fundamental con el control PID es que es un sistema de control de retroalimentación, con parámetros constantes y sin conocimiento directo del proceso, y, por lo tanto, el rendimiento general es reactivo y un compromiso. Si bien el control PID es el mejor controlador para un observador sin un modelo del proceso, se puede obtener un mejor rendimiento modelando abiertamente al actor del proceso sin recurrir a un observador.

Los controladores PID, cuando se utilizan solos, pueden tener un rendimiento deficiente cuando las ganancias del bucle PID deben reducirse para que el sistema de control no se exceda, oscile o se desvíe del valor de ajuste de control. También tienen dificultades en presencia de no linealidades, pueden equilibrar la regulación con el tiempo de respuesta, no reaccionan a los cambios en el comportamiento del proceso (por ejemplo, el proceso cambia después de haberse calentado) y tienen un retraso en la respuesta a grandes perturbaciones.

La mejora más significativa es la incorporación del control de avance con conocimiento del sistema y el uso del PID solo para controlar los errores. Como alternativa, los PID se pueden modificar de formas más menores, como por ejemplo cambiando los parámetros (ya sea mediante la programación de la ganancia en diferentes casos de uso o modificándolos de forma adaptativa en función del rendimiento), mejorando la medición (mayor frecuencia de muestreo, precisión y exactitud, y filtrado de paso bajo si es necesario) o conectando en cascada varios controladores PID.

Linealidad y simetría

Los controladores PID funcionan mejor cuando el circuito a controlar es lineal y simétrico, por lo que su rendimiento en sistemas no lineales y asimétricos se ve reducido.

Por ejemplo, una válvula no lineal en una aplicación de control de caudal dará como resultado una sensibilidad de bucle variable, lo que requerirá una acción amortiguada para evitar la inestabilidad. Una solución es el uso de la característica no lineal de la válvula en el algoritmo de control para compensar esto.

Una aplicación asimétrica, por ejemplo, es el control de temperatura en sistemas HVAC que utilizan solo calefacción activa (a través de un elemento calefactor), donde solo hay refrigeración pasiva disponible. Cuando se desea reducir la temperatura controlada, la salida de calefacción está apagada, pero no hay refrigeración activa debido a la salida de control. Por lo tanto, cualquier exceso de temperatura en aumento solo se puede corregir lentamente; no se puede forzar hacia abajo mediante la salida de control. En este caso, el controlador PID se puede ajustar para que esté sobreamortiguado, para evitar o reducir el exceso, pero esto reduce el rendimiento al aumentar el tiempo de estabilización de una temperatura en aumento hasta el punto de ajuste. La degradación inherente de la calidad del control en esta aplicación se podría resolver mediante la aplicación de refrigeración activa.

Ruido en término derivado

Un problema con el término derivado es que amplifica las mediciones de frecuencia más alta o el ruido del proceso que puede causar grandes cantidades de cambio en la salida. A menudo es útil filtrar las mediciones con un filtro de paso bajo para eliminar los componentes de ruido de frecuencia más alta. Como el filtrado de paso bajo y el control derivado pueden cancelarse entre sí, la cantidad de filtrado es limitada. Por lo tanto, la instrumentación de bajo ruido puede ser importante. Se puede utilizar un filtro mediano no lineal, que mejora la eficiencia del filtrado y el rendimiento práctico. ^[31] En algunos casos, la banda diferencial se puede desactivar con poca pérdida de control. Esto es equivalente a utilizar el controlador PID como un controlador PI.

Modificaciones al algoritmo

El algoritmo PID básico presenta algunos desafíos en las aplicaciones de control que se han abordado mediante modificaciones menores en la forma PID.

Cuerda integral

Un problema común que surge de las implementaciones ideales de PID es el windup integral . Después de un gran cambio en el punto de ajuste, el término integral puede acumular un error mayor que el valor máximo de la variable de regulación (windup), por lo que el sistema se excede y continúa aumentando hasta que se deshaga este error acumulado. Este problema se puede solucionar de la siguiente manera:

• Deshabilitar la integración hasta que el PV haya ingresado a la región controlable
• Evitar que el término integral se acumule por encima o por debajo de límites predeterminados
• Calcular retroactivamente el término integral para restringir la salida del regulador dentro de límites factibles. ^[32]

Sobreimpulso a partir de perturbaciones conocidas

Por ejemplo, se utiliza un bucle PID para controlar la temperatura de un horno de resistencia eléctrica en el que el sistema se ha estabilizado. Ahora, cuando se abre la puerta y se introduce algo frío en el horno, la temperatura cae por debajo del punto de ajuste. La función integral del controlador tiende a compensar el error introduciendo otro error en la dirección positiva. Este exceso se puede evitar congelando la función integral después de la apertura de la puerta durante el tiempo que normalmente necesita el bucle de control para recalentar el horno.

Controlador PI

Bloque básico de un controlador PI

Un controlador PI (controlador proporcional-integral) es un caso especial del controlador PID en el que no se utiliza la derivada (D) del error.

La salida del controlador viene dada por

${\displaystyle K_{P}\Delta +K_{I}\int \Delta \,dt}$

donde es el error o desviación del valor medido real ( PV ) del punto de ajuste ( SP ). ${\displaystyle \Delta }$

${\displaystyle \Delta =SP-PV.}$

Un controlador PI se puede modelar fácilmente en software como Simulink o Xcos utilizando un cuadro de "diagrama de flujo" que involucra operadores de Laplace :

${\displaystyle C={\frac {G(1+\tau s)}{\tau s}}}$

dónde

${\displaystyle G=K_{P}}$= ganancia proporcional

${\displaystyle {\frac {G}{\tau }}=K_{I}}$= ganancia integral

Establecer un valor suele ser un equilibrio entre reducir el sobreimpulso y aumentar el tiempo de estabilización. ${\displaystyle G}$

La falta de acción derivativa puede hacer que el sistema sea más estable en estado estable en el caso de datos ruidosos. Esto se debe a que la acción derivativa es más sensible a los términos de mayor frecuencia en las entradas.

Sin una acción derivada, un sistema controlado por PI responde menos a alteraciones de estado reales (sin ruido) y relativamente rápidas, por lo que el sistema será más lento en alcanzar el punto de ajuste y más lento en responder a las perturbaciones de lo que puede ser un sistema PID bien ajustado.

Banda muerta

Muchos bucles PID controlan un dispositivo mecánico (por ejemplo, una válvula). El mantenimiento mecánico puede ser un costo importante y el desgaste conduce a la degradación del control en forma de fricción estática o juego en la respuesta mecánica a una señal de entrada. La tasa de desgaste mecánico es principalmente una función de la frecuencia con la que se activa un dispositivo para realizar un cambio. Cuando el desgaste es una preocupación importante, el bucle PID puede tener una banda muerta de salida para reducir la frecuencia de activación de la salida (válvula). Esto se logra modificando el controlador para mantener su salida estable si el cambio fuera pequeño (dentro del rango de banda muerta definido). La salida calculada debe salir de la banda muerta antes de que cambie la salida real.

Cambio de paso del punto de ajuste

Los términos proporcional y derivativo pueden producir un movimiento excesivo en la salida cuando un sistema se somete a un aumento escalonado instantáneo del error, como un cambio grande en el punto de ajuste. En el caso del término derivativo, esto se debe a que se toma la derivada del error, que es muy grande en el caso de un cambio escalonado instantáneo. Como resultado, algunos algoritmos PID incorporan algunas de las siguientes modificaciones:

Aumento gradual del punto de ajuste

En esta modificación, el valor de consigna se desplaza gradualmente desde su valor anterior hasta un valor nuevo especificado mediante una función de rampa diferencial lineal o de primer orden. Esto evita la discontinuidad presente en un cambio de paso simple.

Derivada de la variable del proceso

En este caso, el controlador PID mide la derivada del PV medido, en lugar de la derivada del error. Esta cantidad es siempre continua (es decir, nunca sufre un cambio escalonado como resultado de un cambio del punto de ajuste). Esta modificación es un caso simple de ponderación del punto de ajuste.

Ponderación del punto de ajuste

La ponderación del punto de ajuste agrega factores ajustables (generalmente entre 0 y 1) al punto de ajuste en el error del elemento proporcional y derivativo del controlador. El error en el término integral debe ser el error de control real para evitar errores de control de estado estable. Estos dos parámetros adicionales no afectan la respuesta a las perturbaciones de carga y al ruido de medición y se pueden ajustar para mejorar la respuesta del punto de ajuste del controlador.

Retroalimentación hacia adelante

El rendimiento del sistema de control se puede mejorar combinando el control de retroalimentación (o de bucle cerrado) de un controlador PID con el control de avance (o de bucle abierto). El conocimiento sobre el sistema (como la aceleración y la inercia deseadas) se puede transmitir por adelantado y combinar con la salida PID para mejorar el rendimiento general del sistema. El valor de avance por sí solo puede proporcionar a menudo la mayor parte de la salida del controlador. El controlador PID tiene que compensar principalmente cualquier diferencia o error que quede entre el punto de ajuste (SP) y la respuesta del sistema al control de bucle abierto. Dado que la salida de avance no se ve afectada por la retroalimentación del proceso, nunca puede hacer que el sistema de control oscile, mejorando así la respuesta del sistema sin afectar la estabilidad. El avance puede basarse en el punto de ajuste y en perturbaciones medidas adicionales. La ponderación del punto de ajuste es una forma simple de avance.

Por ejemplo, en la mayoría de los sistemas de control de movimiento, para acelerar una carga mecánica bajo control, se requiere más fuerza del actuador. Si se utiliza un controlador PID de bucle de velocidad para controlar la velocidad de la carga y ordenar la fuerza que aplica el actuador, entonces es beneficioso tomar la aceleración instantánea deseada, escalar ese valor de manera apropiada y agregarlo a la salida del controlador de bucle de velocidad PID. Esto significa que siempre que se acelera o desacelera la carga, se ordena una cantidad proporcional de fuerza desde el actuador independientemente del valor de retroalimentación. El bucle PID en esta situación utiliza la información de retroalimentación para cambiar la salida combinada para reducir la diferencia restante entre el punto de ajuste del proceso y el valor de retroalimentación. Al trabajar juntos, el controlador de avance de bucle abierto combinado y el controlador PID de bucle cerrado pueden proporcionar un sistema de control con mayor capacidad de respuesta.

Operación sin problemas

Los controladores PID a menudo se implementan con una característica de inicialización "sin sobresaltos" que recalcula el término acumulador integral para mantener una salida de proceso consistente a través de cambios de parámetros. ^[33] Una implementación parcial es almacenar la ganancia integral multiplicada por el error en lugar de almacenar el error y multiplicarlo posteriormente por la ganancia integral, lo que evita una salida discontinua cuando se cambia la ganancia I, pero no las ganancias P o D.

Otras mejoras

Además de la alimentación hacia adelante, los controladores PID a menudo se mejoran mediante métodos como la programación de ganancia PID (cambio de parámetros en diferentes condiciones de funcionamiento), lógica difusa o lógica de verbos computacionales. ^{[34] [35]} Pueden surgir otros problemas de aplicación práctica de la instrumentación conectada al controlador. Se requiere una frecuencia de muestreo, precisión de medición y exactitud de medición lo suficientemente altas para lograr un rendimiento de control adecuado. Otro método nuevo para mejorar el controlador PID es aumentar el grado de libertad mediante el uso de orden fraccionario . El orden del integrador y el diferenciador agregan mayor flexibilidad al controlador. ^[36]

Control en cascada

Una ventaja distintiva de los controladores PID es que se pueden utilizar dos controladores PID juntos para obtener un mejor rendimiento dinámico. Esto se denomina control PID en cascada. Dos controladores están en cascada cuando están dispuestos de modo que uno regule el punto de ajuste del otro. Un controlador PID actúa como controlador de bucle externo, que controla el parámetro físico primario, como el nivel o la velocidad del fluido. El otro controlador actúa como controlador de bucle interno, que lee la salida del controlador de bucle externo como punto de ajuste, que normalmente controla un parámetro que cambia más rápidamente, el caudal o la aceleración. Se puede demostrar matemáticamente ^{[ cita requerida ]} que la frecuencia de trabajo del controlador aumenta y la constante de tiempo del objeto se reduce mediante el uso de controladores PID en cascada. ^{[ vago ]} .

Por ejemplo, un baño de circulación con control de temperatura tiene dos controladores PID en cascada, cada uno con su propio sensor de temperatura de termopar . El controlador externo controla la temperatura del agua mediante un termopar ubicado lejos del calentador, donde lee con precisión la temperatura de la mayor parte del agua. El término de error de este controlador PID es la diferencia entre la temperatura deseada del baño y la temperatura medida. En lugar de controlar el calentador directamente, el controlador PID externo establece un objetivo de temperatura del calentador para el controlador PID interno. El controlador PID interno controla la temperatura del calentador mediante un termopar conectado al calentador. El término de error del controlador interno es la diferencia entre este punto de ajuste de temperatura del calentador y la temperatura medida del calentador. Su salida controla el calentador real para que se mantenga cerca de este punto de ajuste.

Los términos proporcionales, integrales y diferenciales de los dos controladores serán muy diferentes. El controlador PID externo tiene una constante de tiempo larga: toda el agua del tanque debe calentarse o enfriarse. El circuito interno responde mucho más rápido. Cada controlador se puede ajustar para que coincida con la física del sistema que controla (transferencia de calor y masa térmica de todo el tanque o solo del calentador), lo que brinda una mejor respuesta total. ^{[37] [38]}

Nomenclatura y formas alternativas

Forma estándar versus forma paralela (ideal)

La forma del controlador PID que se encuentra con más frecuencia en la industria y la más relevante para los algoritmos de ajuste es la forma estándar . En esta forma, la ganancia se aplica a los términos , y , lo que da como resultado: ${\displaystyle K_{p}}$ ${\displaystyle I_{\mathrm {out} }}$ ${\displaystyle D_{\mathrm {out} }}$

${\displaystyle u(t)=K_{p}\left(e(t)+{\frac {1}{T_{i}}}\int _{0}^{t}e(\tau )\,d\tau +T_{d}{\frac {d}{dt}}e(t)\right)}$

dónde

${\displaystyle T_{i}}$es el tiempo integral

${\displaystyle T_{d}}$es la derivada del tiempo

En esta forma estándar, los parámetros tienen un significado físico claro. En particular, la suma interna produce un nuevo valor de error único que se compensa con los errores pasados ​​y futuros. El término de error proporcional es el error actual. El término de componentes derivados intenta predecir el valor de error en segundos (o muestras) en el futuro, suponiendo que el control de bucle permanece sin cambios. El componente integral ajusta el valor de error para compensar la suma de todos los errores pasados, con la intención de eliminarlos por completo en segundos (o muestras). El valor de error único compensado resultante se escala luego por la ganancia única para calcular la variable de control. ${\displaystyle T_{d}}$ ${\displaystyle T_{i}}$ ${\displaystyle K_{p}}$

En la forma paralela, que se muestra en la sección de teoría del controlador

${\displaystyle u(t)=K_{p}e(t)+K_{i}\int _{0}^{t}e(\tau )\,d\tau +K_{d}{\frac {d}{dt}}e(t)}$

Los parámetros de ganancia se relacionan con los parámetros de la forma estándar a través de y . Esta forma paralela, donde los parámetros se tratan como ganancias simples, es la forma más general y flexible. Sin embargo, también es la forma donde los parámetros tienen la relación más débil con los comportamientos físicos y generalmente se reserva para el tratamiento teórico del controlador PID. La forma estándar, a pesar de ser ligeramente más compleja matemáticamente, es más común en la industria. ${\displaystyle K_{i}=K_{p}/T_{i}}$ ${\displaystyle K_{d}=K_{p}T_{d}}$

Ganancia recíproca, también conocida como banda proporcional

En muchos casos, la variable manipulada que genera el controlador PID es una fracción adimensional entre 0 y 100% de algún valor máximo posible, y la traducción a unidades reales (como la tasa de bombeo o los vatios de potencia del calentador) está fuera del controlador PID. Sin embargo, la variable de proceso está en unidades adimensionales como la temperatura. Es común en este caso expresar la ganancia no como "salida por grado", sino en la forma recíproca de una banda proporcional , que es "grados por salida completa": el rango en el que la salida cambia de 0 a 1 (0% a 100%). Más allá de este rango, la salida está saturada, completamente apagada o completamente encendida. Cuanto más estrecha sea esta banda, mayor será la ganancia proporcional. ${\displaystyle K_{p}}$ ${\displaystyle 100/K_{p}}$

Basar la acción derivada en PV

En la mayoría de los sistemas de control comerciales, la acción derivativa se basa en la variable de proceso y no en el error. Es decir, un cambio en el punto de ajuste no afecta la acción derivativa. Esto se debe a que la versión digitalizada del algoritmo produce un gran pico no deseado cuando se cambia el punto de ajuste. Si el punto de ajuste es constante, los cambios en la variable de proceso serán los mismos que los cambios en el error. Por lo tanto, esta modificación no afecta la forma en que el controlador responde a las perturbaciones del proceso.

Basar la acción proporcional en la PV

La mayoría de los sistemas de control comerciales ofrecen la opción de basar también la acción proporcional únicamente en la variable de proceso. Esto significa que sólo la acción integral responde a los cambios en el punto de ajuste. La modificación del algoritmo no afecta la forma en que el controlador responde a las perturbaciones del proceso. Basar la acción proporcional en la variable de proceso elimina el cambio instantáneo y posiblemente muy grande en la salida causado por un cambio repentino en el punto de ajuste. Dependiendo del proceso y del ajuste, esto puede ser beneficioso para la respuesta a un paso del punto de ajuste.

${\displaystyle \mathrm {MV(t)} =K_{p}\left(\,{-PV(t)}+{\frac {1}{T_{i}}}\int _{0}^{t}{e(\tau )}\,{d\tau }-T_{d}{\frac {d}{dt}}PV(t)\right)}$

King ^[39] describe un método eficaz basado en gráficos.

Forma de Laplace

A veces es útil escribir el regulador PID en forma de transformada de Laplace :

${\displaystyle G(s)=K_{p}+{\frac {K_{i}}{s}}+K_{d}{s}={\frac {K_{d}{s^{2}}+K_{p}{s}+K_{i}}{s}}}$

Tener el controlador PID escrito en forma Laplace y tener la función de transferencia del sistema controlado hace que sea fácil determinar la función de transferencia de circuito cerrado del sistema.

Serie/forma de interacción

Otra representación del controlador PID es la serie, o forma interactuante .

${\displaystyle G(s)=K_{c}({\frac {1}{\tau _{i}{s}}}+1)(\tau _{d}{s}+1)}$

donde los parámetros están relacionados con los parámetros de la forma estándar a través de

${\displaystyle K_{p}=K_{c}\cdot \alpha }$, , y ${\displaystyle T_{i}=\tau _{i}\cdot \alpha }$

${\displaystyle T_{d}={\frac {\tau _{d}}{\alpha }}}$

con

${\displaystyle \alpha =1+{\frac {\tau _{d}}{\tau _{i}}}}$.

Este formato consta básicamente de un controlador PD y PI en serie. Como se requiere la integral para calcular la polarización del controlador, este formato brinda la capacidad de rastrear un valor de polarización externo que se requiere para la implementación adecuada de esquemas de control avanzados con múltiples controladores.

Implementación discreta

El análisis para diseñar una implementación digital de un controlador PID en un microcontrolador (MCU) o dispositivo FPGA requiere que se discretice la forma estándar del controlador PID . ^[40] Las aproximaciones para las derivadas de primer orden se realizan mediante diferencias finitas hacia atrás y se discretizan con un período de muestreo , k es el índice de muestra. ${\displaystyle u(t)}$ ${\displaystyle e(t)}$ ${\displaystyle \Delta t}$

Diferenciando ambos lados de la ecuación PID usando la notación de Newton obtenemos:

${\displaystyle {\dot {u}}(t)=K_{p}{\dot {e}}(t)+K_{i}e(t)+K_{d}{\ddot {e}}(t)}$

Los términos derivados se aproximan como,

${\displaystyle {\dot {f}}(t_{k})={\dfrac {df(t_{k})}{dt}}={\dfrac {f(t_{k})-f(t_{k-1})}{\Delta t}}}$

Entonces,

${\displaystyle {\frac {u(t_{k})-u(t_{k-1})}{\Delta t}}=K_{p}{\frac {e(t_{k})-e(t_{k-1})}{\Delta t}}+K_{i}e(t_{k})+K_{d}{\frac {{\dot {e}}(t_{k})-{\dot {e}}(t_{k-1})}{\Delta t}}}$

Aplicando nuevamente la diferencia hacia atrás obtenemos:

${\displaystyle {\frac {u(t_{k})-u(t_{k-1})}{\Delta t}}=K_{p}{\frac {e(t_{k})-e(t_{k-1})}{\Delta t}}+K_{i}e(t_{k})+K_{d}{\frac {{\frac {e(t_{k})-e(t_{k-1})}{\Delta t}}-{\frac {e(t_{k-1})-e(t_{k-2})}{\Delta t}}}{\Delta t}}}$

Simplificando y reagrupando términos de la ecuación anterior, finalmente se obtiene un algoritmo para una implementación del controlador PID discretizado en una MCU:

${\displaystyle u(t_{k})=u(t_{k-1})+\left(K_{p}+K_{i}\Delta t+{\dfrac {K_{d}}{\Delta t}}\right)e(t_{k})+\left(-K_{p}-{\dfrac {2K_{d}}{\Delta t}}\right)e(t_{k-1})+{\dfrac {K_{d}}{\Delta t}}e(t_{k-2})}$

o:

${\displaystyle u(t_{k})=u(t_{k-1})+K_{p}\left[\left(1+{\dfrac {\Delta t}{T_{i}}}+{\dfrac {T_{d}}{\Delta t}}\right)e(t_{k})+\left(-1-{\dfrac {2T_{d}}{\Delta t}}\right)e(t_{k-1})+{\dfrac {T_{d}}{\Delta t}}e(t_{k-2})\right]}$

calle ${\displaystyle T_{i}=K_{p}/K_{i},T_{d}=K_{d}/K_{p}}$

Nota: Este método resuelve de hecho donde es una constante independiente de t. Esta constante es útil cuando se desea tener un control de inicio y detención en el bucle de regulación. Por ejemplo, al establecer Kp, Ki y Kd en 0, se mantendrá u(t) constante. Del mismo modo, cuando se desea iniciar una regulación en un sistema donde el error ya está cerca de 0 con u(t) no nulo, se evita enviar la salida a 0. ${\displaystyle u(t)=K_{\text{p}}e(t)+K_{\text{i}}\int _{0}^{t}e(\tau )\,\mathrm {d} \tau +K_{\text{d}}{\frac {\mathrm {d} e(t)}{\mathrm {d} t}}+u_{0}}$ ${\displaystyle u_{0}}$

Pseudocódigo

A continuación se muestra un grupo muy simple y explícito de pseudocódigo que puede ser fácilmente comprendido por el profano: ^{[ cita requerida ]}

• Kp - ganancia proporcional
• Ki - ganancia integral
• Kd - ganancia derivada
• dt - tiempo de intervalo de bucle (supone una escala razonable) ^[b]

error_anterior := 0integral := 0bucle: error := punto de ajuste − valor medido proporcional := error; integral := integral + error × dt derivada := (error - error_anterior) / dt salida := Kp × proporcional + Ki × integral + Kd × derivada error_anterior := error esperar(dt) Ir al bucle

A continuación se muestra un pseudocódigo que ilustra cómo implementar un PID considerando el PID como un filtro IIR :

La transformada Z de un PID se puede escribir como ( es el tiempo de muestreo): ${\displaystyle \Delta _{t}}$

${\displaystyle C(z)=K_{p}+K_{i}\Delta _{t}{\frac {z}{z-1}}+{\frac {K_{d}}{\Delta _{t}}}{\frac {z-1}{z}}}$

y expresado en forma IIR (de acuerdo con la implementación discreta mostrada arriba):

${\displaystyle C(z)={\frac {\left(K_{p}+K_{i}\Delta _{t}+{\dfrac {K_{d}}{\Delta _{t}}}\right)+\left(-K_{p}-{\dfrac {2K_{d}}{\Delta _{t}}}\right)z^{-1}+{\dfrac {K_{d}}{\Delta _{t}}}z^{-2}}{1-z^{-1}}}}$

Podemos entonces deducir la iteración recursiva que a menudo se encuentra en la implementación de FPGA ^[41]

${\displaystyle u[n]=u[n-1]+\left(K_{p}+K_{i}\Delta _{t}+{\dfrac {K_{d}}{\Delta _{t}}}\right)\epsilon [n]+\left(-K_{p}-{\dfrac {2K_{d}}{\Delta _{t}}}\right)\epsilon [n-1]+{\dfrac {K_{d}}{\Delta _{t}}}\epsilon [n-2]}$

A0 := Kp + Ki*dt + Kd/dtA1 := -Kp - 2*Kd/dtA2 := Kd/dterror[2] := 0 // e(t-2)error[1] := 0 // e(t-1)error[0] := 0 // e(t)salida := u0 // Generalmente el valor actual del actuadorbucle: error[2] := error[1] error[1] := error[0] error[0] := punto de ajuste − valor medido salida := salida + A0 * error[0] + A1 * error[1] + A2 * error[2] esperar(dt) Ir al bucle

Aquí, Kp es un número adimensional, Ki se expresa en y Kd se expresa en s. Cuando se realiza una regulación en la que el actuador y el valor medido no están en la misma unidad (por ejemplo, regulación de temperatura utilizando un motor que controla una válvula), Kp, Ki y Kd se pueden corregir mediante un factor de conversión de unidades. También puede ser interesante utilizar Ki en su forma recíproca (tiempo de integración). La implementación anterior permite realizar un controlador solo I que puede ser útil en algunos casos. ${\displaystyle s^{-1}}$

En el mundo real, esto se convierte de D a A y se pasa al proceso bajo control como variable manipulada (MV). El error actual se almacena en otro lugar para reutilizarlo en la siguiente diferenciación; luego, el programa espera hasta que hayan pasado dt segundos desde el inicio y el bucle comienza nuevamente, leyendo nuevos valores para la PV y el punto de ajuste y calculando un nuevo valor para el error. ^[42]

Tenga en cuenta que para el código real, el uso de "wait(dt)" puede ser inapropiado porque no tiene en cuenta el tiempo que tarda el algoritmo en el bucle o, lo que es más importante, cualquier interrupción que retrase el algoritmo.

Un problema común durante el uso es la respuesta a la derivada de un borde ascendente o descendente del punto de ajuste, como se muestra a continuación: ${\displaystyle K_{d}}$

Una solución alternativa típica es filtrar la acción derivada utilizando un filtro de paso bajo de constante de tiempo donde : ${\displaystyle \tau _{d}/N}$ ${\displaystyle 3<=N<=10}$

Una variante del algoritmo anterior que utiliza un filtro de respuesta de impulso infinito (IIR) para la derivada:

A0 := Kp + Ki*dtA1 :=-Kperror[2] := 0 // e(t-2)error[1] := 0 // e(t-1)error[0] := 0 // e(t)salida := u0 // Generalmente el valor actual del actuadorA0d := Kd/dtA1d := - 2,0*Kd/dtA2d := Kd/dtNúmero := 5tau := Kd / (Kp*N) // Constante de tiempo del filtro IIRalfa := dt / (2*tau)d0 := 0d1 := 0fd0 := 0fd1 := 0bucle: error[2] := error[1] error[1] := error[0] error[0] := punto de ajuste − valor medido // Investigador principal salida := salida + A0 * error[0] + A1 * error[1] // D filtrado d1 := d0 d0 := A0d * error[0] + A1d * error[1] + A2d * error[2] fd1 := fd0 fd0 := ((alfa) / (alfa + 1)) * (d0 + d1) - ((alfa - 1) / (alfa + 1)) * fd1 salida := salida + fd0  esperar(dt) Ir al bucle

Véase también

• Teoría del control
• Control de rechazo de perturbaciones activas

Notas

1. La única excepción es cuando el valor objetivo es el mismo que el valor obtenido cuando la salida del controlador es cero.
2. Tenga en cuenta que para intervalos muy pequeños (por ejemplo, 60 Hz/ segundo), el valor de la derivada resultante será extremadamente grande y órdenes de magnitud mayor que los componentes proporcionales o integrales. Es probable que ajustar este valor para la derivada (por ejemplo, multiplicando por 1000) o cambiar la división por multiplicación arroje los resultados deseados. Esto es válido para todo el pseudocódigo presentado aquí. ${\textstyle .016{\bar {6}}}$

Referencias

1. Araki, M. (2009). "Sistemas de control, robótica y automatización – Volumen VII – Control PID" (PDF) . Japón: Universidad de Kioto.
2. "9.3: Ajuste de PID mediante métodos clásicos". Ingeniería LibreTexts . 2020-05-19 . Consultado el 2024-05-31 .
3. Hills, Richard L (1996), Energía del viento , Cambridge University Press
4. Richard E. Bellman (8 de diciembre de 2015). Procesos de control adaptativo: una visita guiada. Princeton University Press. ISBN 9781400874668.
5. Bennett, Stuart (1996). "Una breve historia del control automático" (PDF) . Revista IEEE Control Systems . 16 (3): 17–25. doi :10.1109/37.506394. Archivado desde el original (PDF) el 2016-08-09 . Consultado el 2014-08-21 .
6. Maxwell, JC (1868). "Sobre los gobernadores" (PDF) . Actas de la Royal Society . 100 .
7. Newpower, Anthony (2006). Hombres de hierro y peces de hojalata: la carrera por construir un mejor torpedo durante la Segunda Guerra Mundial . Praeger Security International. ISBN 978-0-275-99032-9.p. citando a Gray, Edwyn (1991), El dispositivo del diablo: Robert Whitehead y la historia del torpedo , Annapolis, MD: US Naval Institute, p. 33.
8. Sleeman, CW (1880), Torpedoes and Torpedo Warfare, Portsmouth: Griffin & Co., págs. 137-138, que constituye lo que se denomina el secreto del torpedo de pez.
9. "Una breve historia de la automatización de edificios". Archivado desde el original el 8 de julio de 2011. Consultado el 4 de abril de 2011 .
10. Minorsky, Nicolas (1922). "Estabilidad direccional de cuerpos gobernados automáticamente". Revista de la Sociedad Americana de Ingenieros Navales . 34 (2): 280–309. doi :10.1111/j.1559-3584.1922.tb04958.x.
11. Bennett 1993, pág. 67 harvnb error: no target: CITEREFBennett1993 (help)
12. Bennett, Stuart (junio de 1986). Una historia de la ingeniería de control, 1800-1930 . IET. págs. 142-148. ISBN 978-0-86341-047-5.
13. Shinskey, F Greg (2004), El poder de la retroalimentación de reinicio externo (PDF) , Control Global
14. Neuhaus, Rudolf. "Bloqueo de láser de diodo y estrechamiento del ancho de línea" (PDF) . Consultado el 8 de junio de 2015 .
15. "Sistema de control de posición" (PDF) . Departamento de Ingeniería Eléctrica y Electrónica de la Universidad Hacettepe. Archivado desde el original (PDF) el 13 de mayo de 2014.
16. Kebriaei, Reza; Frischkorn, Jan; Reese, Stefanie; Husmann, Tobias; Meier, Horst; Moll, Heiko; Theisen, Werner (2013). "Modelado numérico de recubrimientos pulvimetalúrgicos en piezas con forma de anillo integrados con laminado de anillos". Tecnología de procesamiento de materiales . 213 (1): 2015–2032. doi :10.1016/j.jmatprotec.2013.05.023.
17. Lipták, Béla G. (2003). Instrument Engineers' Handbook: Process control and optimized (4.ª ed.). CRC Press. pág. 108. ISBN 0-8493-1081-4.
18. "Introducción: Diseño de controladores PID". Universidad de Michigan.
19. Tim Wescott (octubre de 2000). «PID sin doctorado» (PDF) . EE Times-India. {{cite journal}}: Requiere citar revista |journal=( ayuda )
20. Bechhoefer, John (2005). "Retroalimentación para físicos: un ensayo tutorial sobre control". Reseñas de física moderna . 77 (3): 783–835. Bibcode :2005RvMP...77..783B. CiteSeerX 10.1.1.124.7043 . doi :10.1103/revmodphys.77.783. 
21. Skogestad, Sigurd (2003). "Reglas analíticas simples para la reducción de modelos y el ajuste de controladores PID" (PDF) .
22. "Una revisión de los métodos de autoajuste de relés para el ajuste de controladores de tipo PID".
23. Kiam Heong Ang; Chong, G.; Yun Li (2005). "Análisis, diseño y tecnología de sistemas de control PID" (PDF) . IEEE Transactions on Control Systems Technology . 13 (4): 559–576. doi :10.1109/TCST.2005.847331. S2CID  921620.
24. Jinghua Zhong (primavera de 2006). "Ajuste del controlador PID: un breve tutorial" (PDF) . Archivado desde el original (PDF) el 21 de abril de 2015. Consultado el 4 de abril de 2011 . {{cite journal}}: Requiere citar revista |journal=( ayuda )
25. Åström, KJ; Hägglund, T. (julio de 1984). "Sintonización automática de reguladores simples". Volúmenes de actas de la IFAC . 17 (2): 1867–1872. doi : 10.1016/S1474-6670(17)61248-5 .
26. Hornsey, Stephen (29 de octubre de 2012). "Una revisión de los métodos de autoajuste de relés para el ajuste de controladores de tipo PID". Reinvención . 5 (2).
27. Bequette, B. Wayne (2003). Control de procesos: modelado, diseño y simulación . Upper Saddle River, Nueva Jersey: Prentice Hall. pág. 129. ISBN 978-0-13-353640-9.
28. Heinänen, Eero (octubre de 2018). Un método para el ajuste automático de un controlador PID siguiendo la optimización de Luus-Jaakola (PDF) (edición de tesis de maestría). Tampere, Finlandia: Universidad Tecnológica de Tampere . Consultado el 1 de febrero de 2019 .
29. Li, Yun; Ang, Kiam Heong; Chong, Gregory CY (febrero de 2006). "Patentes, software y hardware para control PID: una descripción general y análisis del estado actual" (PDF) . Revista IEEE Control Systems . 26 (1): 42–54. doi :10.1109/MCS.2006.1580153. S2CID  18461921.
30. Soltesz, Kristian (enero de 2012). Sobre la automatización del procedimiento de ajuste PID ( Licentiate theis). Universidad de Lund . 847ca38e-93e8-4188-b3d5-8ec6c23f2132.
31. Li, Y. y Ang, KH y Chong, GCY (2006) Análisis y diseño de sistemas de control PID: problemas, soluciones y direcciones futuras. Revista IEEE Control Systems, 26 (1). pp. 32-41. ISSN  0272-1708
32. Cooper, Douglas. "Integral (Reset) Windup, Jacketing Logic and the Velocity PI Form" (Desarrollador integral (reinicio), lógica de encamisado y la forma PI de velocidad) . Consultado el 18 de febrero de 2014 .
33. Cooper, Douglas. "Control PI del intercambiador de calor". Control de procesos prácticos por Control Guru . Consultado el 27 de febrero de 2014 .
34. Yang, T. (junio de 2005). "Arquitecturas de controladores de verbos computacionales: hacia un nuevo paradigma de control inteligente". Revista internacional de cognición computacional . 3 (2): 74–101. CiteSeerX 10.1.1.152.9564 . 
35. Liang, Yilong; Yang, Tao (2009). "Control de recocedor de combustible mediante controladores PID de verbos computacionales". Actas de la 3.ª Conferencia internacional sobre lucha contra la falsificación, seguridad e identificación en las comunicaciones . Asid'09: 417–420. ISBN 9781424438839.
36. Tenreiro Machado JA, et al. (2009). "Algunas aplicaciones del cálculo fraccionario en ingeniería". Problemas matemáticos en ingeniería . 2010 : 1–34. doi : 10.1155/2010/639801 . hdl : 10400.22/4306 .
37. [1] Fundamentos del control en cascada | A veces, dos controladores pueden hacer un mejor trabajo para mantener una variable de proceso donde se desea. | Por Vance VanDoren, PHD, PE | 17 DE AGOSTO DE 2014
38. [2] | Los beneficios del control en cascada | 22 de septiembre de 2020 | Watlow
39. King, Myke (2011). Control de procesos: un enfoque práctico . Wiley. págs. 52–78. ISBN 978-0-470-97587-9.
40. "Diseño y análisis de controladores PI y PID discretos para implementación digital" . Scribd.com . Consultado el 4 de abril de 2011 .
41. Thakur, Bhushana. Implementación de hardware de un controlador PID basado en FPGA (PDF) .
42. "Control de procesos PID, un ejemplo de "Control de crucero"". CodeProject. 2009. Consultado el 4 de noviembre de 2012 .

• Bequette, B. Wayne (2006). Control de procesos: modelado, diseño y simulación . Prentice Hall PTR. ISBN 9789861544779.

Lectura adicional

• Liptak, Bela (1995). Instrument Engineers' Handbook: Process Control (Manual del ingeniero de instrumentos: control de procesos) . Radnor, Pensilvania: Chilton Book Company. Págs. 20-29. ISBN. 978-0-8019-8242-2.
• Tan, Kok Kiong; Wang Qing-Guo; Cuelga Chang Chieh (1999). Avances en Control PID . Londres, Reino Unido: Springer-Verlag. ISBN 978-1-85233-138-2.
• King, Myke (2010). Control de procesos: un enfoque práctico. Chichester, Reino Unido: John Wiley & Sons Ltd. ISBN 978-0-470-97587-9.
• Van Doren, Vance J. (1 de julio de 2003). "Fundamentos del ajuste de bucles". Ingeniería de control .
• Sellers, David. "Una visión general del control proporcional más integral más derivativo y sugerencias para su aplicación e implementación exitosas" (PDF) . Archivado desde el original (PDF) el 7 de marzo de 2007. Consultado el 5 de mayo de 2007 .
• Graham, Ron; Mike McHugh (3 de octubre de 2005). "Preguntas frecuentes sobre el ajuste del controlador PID". Mike McHugh. Archivado desde el original el 6 de febrero de 2005. Consultado el 5 de enero de 2009 .
• Aidan O'Dwyer (2009). Manual de reglas de ajuste de controladores PI y PID (PDF) (3.ª ed.). Imperial College Press. ISBN 978-1-84816-242-6.

Enlaces externos

• Ajuste de PID con Mathematica
• Ajuste de PID con Python
• Principios de control y ajuste PID
• Introducción a los términos clave asociados con el control de temperatura PID

Tutoriales de PID

• Control PID en MATLAB/Simulink y Python con TCLab
• ¿Qué es todo esto del PID? Artículo en Electronic Design
• Muestra cómo construir un controlador PID con componentes electrónicos básicos (pág. 22)
• PID sin doctorado
• Control PID con MATLAB y Simulink
• PID con amplificador operacional único
• Métodos probados y mejores prácticas para el control PID
• Principios de control y ajuste PID
• Guía de ajuste de PID: un enfoque de mejores prácticas para comprender y ajustar los controladores PID
• Michael Barr (30 de julio de 2002), Introducción al control de lazo cerrado, Programación de sistemas integrados, archivado desde el original el 9 de febrero de 2010
• Jinghua Zhong, Ingeniería mecánica, Universidad de Purdue (primavera de 2006). "Ajuste del controlador PID: un breve tutorial" (PDF) . Archivado desde el original (PDF) el 2015-04-21 . Consultado el 2013-12-04 .{{cite web}}: CS1 maint: multiple names: authors list (link)
• Introducción a los controladores P, PI, PD y PID con MATLAB