Aprendizaje no supervisado

El aprendizaje no supervisado es un marco de aprendizaje automático en el que, a diferencia del aprendizaje supervisado , los algoritmos aprenden patrones exclusivamente a partir de datos no etiquetados. ^[1] Otros marcos en el espectro de las supervisiones incluyen la supervisión débil o semisupervisión , donde se etiqueta una pequeña parte de los datos, y la autosupervisión . Algunos investigadores consideran que el aprendizaje autosupervisado es una forma de aprendizaje no supervisado. ^[2]

En términos conceptuales, el aprendizaje no supervisado se divide en los aspectos de datos, entrenamiento, algoritmo y aplicaciones posteriores. Normalmente, el conjunto de datos se obtiene de forma económica "en la naturaleza", como un corpus de texto masivo obtenido mediante rastreo web , con solo un filtrado menor (como Common Crawl ). Esto se compara favorablemente con el aprendizaje supervisado, donde el conjunto de datos (como ImageNet1000 ) generalmente se construye manualmente, lo que es mucho más costoso.

Hubo algoritmos diseñados específicamente para el aprendizaje no supervisado, como algoritmos de agrupamiento como k-means , técnicas de reducción de dimensionalidad como el análisis de componentes principales (PCA) , aprendizaje automático de Boltzmann y autocodificadores . Después del auge del aprendizaje profundo, la mayor parte del aprendizaje no supervisado a gran escala se ha realizado mediante el entrenamiento de arquitecturas de redes neuronales de propósito general por descenso de gradiente , adaptadas para realizar aprendizaje no supervisado mediante el diseño de un procedimiento de entrenamiento adecuado.

A veces, un modelo entrenado se puede utilizar tal cual, pero lo más frecuente es que se modifique para aplicaciones posteriores. Por ejemplo, el método de preentrenamiento generativo entrena un modelo para generar un conjunto de datos textuales, antes de ajustarlo para otras aplicaciones, como la clasificación de texto. ^[3]^[4] Como otro ejemplo, los autocodificadores se entrenan para obtener buenas características , que luego se pueden usar como un módulo para otros modelos, como en un modelo de difusión latente .

Tareas

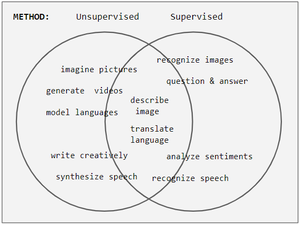
Las tareas se suelen clasificar como discriminativas (reconocimiento) o generativas (imaginación). A menudo, pero no siempre, las tareas discriminativas utilizan métodos supervisados y las tareas generativas utilizan métodos no supervisados (véase el diagrama de Venn ); sin embargo, la separación es muy difusa. Por ejemplo, el reconocimiento de objetos favorece el aprendizaje supervisado, pero el aprendizaje no supervisado también puede agrupar objetos en grupos. Además, a medida que avanza el progreso, algunas tareas emplean ambos métodos, y algunas tareas oscilan entre uno y otro. Por ejemplo, el reconocimiento de imágenes comenzó siendo muy supervisado, pero se convirtió en híbrido al emplear un preentrenamiento no supervisado, y luego pasó a la supervisión nuevamente con la llegada de dropout , ReLU y las tasas de aprendizaje adaptativo .

Una tarea generativa típica es la siguiente: en cada paso, se toma una muestra de un punto de datos del conjunto de datos, se elimina una parte de los datos y el modelo debe inferir la parte eliminada. Esto es particularmente claro para los autocodificadores de eliminación de ruido y BERT .

Arquitecturas de redes neuronales

Capacitación

Durante la fase de aprendizaje, una red no supervisada intenta imitar los datos que se le proporcionan y utiliza el error en su salida imitada para corregirse a sí misma (es decir, corregir sus ponderaciones y sesgos). A veces, el error se expresa como una baja probabilidad de que se produzca la salida errónea, o puede expresarse como un estado inestable de alta energía en la red.

A diferencia del uso dominante de la retropropagación en los métodos supervisados , el aprendizaje no supervisado también emplea otros métodos, entre ellos: la regla de aprendizaje de Hopfield, la regla de aprendizaje de Boltzmann, la divergencia contrastiva , el sueño-vigilia , la inferencia variacional , la máxima verosimilitud , el máximo a posteriori , el muestreo de Gibbs y la retropropagación de errores de reconstrucción o reparametrizaciones de estados ocultos. Consulte la tabla siguiente para obtener más detalles.

Energía

Una función de energía es una medida macroscópica del estado de activación de una red. En las máquinas de Boltzmann, desempeña el papel de la función de costo. Esta analogía con la física está inspirada en el análisis de Ludwig Boltzmann de la energía macroscópica de un gas a partir de las probabilidades microscópicas de movimiento de partículas , donde k es la constante de Boltzmann y T es la temperatura. En la red RBM la relación es , ^[5] donde y varían en cada patrón de activación posible y . Para ser más precisos, , donde es un patrón de activación de todas las neuronas (visibles y ocultas). Por lo tanto, algunas redes neuronales tempranas llevan el nombre de máquina de Boltzmann. Paul Smolensky llama a la armonía . Una red busca baja energía que es alta armonía. $p\propto e^{-E/kT}$ $p=e^{-E}/Z$ $p$ $E$ $\textstyle {Z=\sum _{\scriptscriptstyle {\text{All Patterns}}}e^{-E({\text{pattern}})}}$ $p(a)=e^{-E(a)}/Z$ $a$ $-E\,$

Redes

Esta tabla muestra diagramas de conexión de varias redes no supervisadas, cuyos detalles se darán en la sección Comparación de redes. Los círculos son neuronas y los bordes entre ellos son pesos de conexión. A medida que cambia el diseño de la red, se agregan características para habilitar nuevas capacidades o se eliminan para acelerar el aprendizaje. Por ejemplo, las neuronas cambian entre deterministas (Hopfield) y estocásticas (Boltzmann) para permitir una salida robusta, se eliminan pesos dentro de una capa (RBM) para acelerar el aprendizaje o se permite que las conexiones se vuelvan asimétricas (Helmholtz).

De las redes que llevan nombres de personas, sólo Hopfield trabajó directamente con redes neuronales. Boltzmann y Helmholtz fueron los primeros en desarrollar redes neuronales artificiales, pero su trabajo en física y fisiología inspiró los métodos analíticos que se utilizaron.

Historia

Redes específicas

A continuación, destacamos algunas características de redes seleccionadas. Los detalles de cada una se muestran en la siguiente tabla comparativa.

Red Hopfield: Redes de Hopfield inspiradas en el ferromagnetismo. Una neurona corresponde a un dominio de hierro con momentos magnéticos binarios Arriba y Abajo, y las conexiones neuronales corresponden a la influencia de los dominios entre sí. Las conexiones simétricas permiten una formulación de energía global. Durante la inferencia, la red actualiza cada estado utilizando la función de paso de activación estándar. Los pesos simétricos y las funciones de energía correctas garantizan la convergencia a un patrón de activación estable. Los pesos asimétricos son difíciles de analizar. Las redes de Hopfield se utilizan como memorias direccionables por contenido (CAM).
Máquina de Boltzmann: Se trata de redes de Hopfield estocásticas. Su valor de estado se obtiene de esta función de densidad de probabilidad de la siguiente manera: supongamos que una neurona binaria se activa con la probabilidad de Bernoulli p(1) = 1/3 y se detiene con p(0) = 2/3. Se obtiene una muestra de ella tomando un número aleatorio distribuido uniformemente y y sustituyéndolo en la función de distribución acumulativa invertida , que en este caso es la función escalonada con un umbral de 2/3. La función inversa = { 0 si x <= 2/3, 1 si x > 2/3 }.
Red de creencias sigmoideas: Introducida por Radford Neal en 1992, esta red aplica ideas de modelos gráficos probabilísticos a redes neuronales. Una diferencia clave es que los nodos en los modelos gráficos tienen significados preasignados, mientras que las características de las neuronas de Belief Net se determinan después del entrenamiento. La red es un gráfico acíclico dirigido escasamente conectado compuesto de neuronas estocásticas binarias. La regla de aprendizaje proviene de la máxima verosimilitud en p(X): Δw _ij s _j * (s _i - p _i ), donde p _i = 1 / ( 1 + e ^{entradas ponderadas en la neurona i} ). s _j son activaciones de una muestra imparcial de la distribución posterior y esto es problemático debido al problema de Explaining Away planteado por Judea Perl. Los métodos bayesianos variacionales utilizan una distribución posterior sustituta y descaradamente ignoran esta complejidad. $\propto$
Red de creencias profundas: Introducida por Hinton, esta red es un híbrido de RBM y red de creencias sigmoideas. Las 2 capas superiores son una RBM y la segunda capa hacia abajo forma una red de creencias sigmoideas. Se la entrena mediante el método RBM apilado y luego se descartan los pesos de reconocimiento que se encuentran debajo de la RBM superior. A partir de 2009, 3 o 4 capas parecen ser la profundidad óptima. ^[6]
Máquina de Helmholtz: Estas son inspiraciones tempranas para los codificadores automáticos variacionales. Sus 2 redes se combinan en una: los pesos hacia adelante operan el reconocimiento y los pesos hacia atrás implementan la imaginación. Es quizás la primera red en hacer ambas cosas. Helmholtz no trabajó en aprendizaje automático, pero inspiró la visión de "motor de inferencia estadística cuya función es inferir causas probables de la entrada sensorial". ^[7] La neurona binaria estocástica genera una probabilidad de que su estado sea 0 o 1. La entrada de datos normalmente no se considera una capa, pero en el modo de generación de máquinas de Helmholtz, la capa de datos recibe la entrada de la capa intermedia y tiene pesos separados para este propósito, por lo que se considera una capa. Por lo tanto, esta red tiene 3 capas.
Autocodificador variacional: Estos están inspirados en las máquinas de Helmholtz y combinan redes de probabilidad con redes neuronales. Un autocodificador es una red CAM de 3 capas, donde se supone que la capa intermedia es una representación interna de patrones de entrada. La red neuronal del codificador es una distribución de probabilidad q _φ (z dado x) y la red del decodificador es p _θ (x dado z). Los pesos se denominan phi y theta en lugar de W y V como en Helmholtz, una diferencia cosmética. Estas 2 redes aquí pueden estar completamente conectadas o usar otro esquema NN.

Comparación de redes

Aprendizaje Hebbiano, ARTE, SOM

El ejemplo clásico de aprendizaje no supervisado en el estudio de redes neuronales es el principio de Donald Hebb , es decir, las neuronas que se activan juntas se conectan entre sí. ^[8] En el aprendizaje hebbiano , la conexión se refuerza independientemente de un error, pero es exclusivamente una función de la coincidencia entre los potenciales de acción entre las dos neuronas. ^[9] Una versión similar que modifica los pesos sinápticos tiene en cuenta el tiempo entre los potenciales de acción ( plasticidad dependiente del tiempo de pico o STDP). Se ha planteado la hipótesis de que el aprendizaje hebbiano subyace a una variedad de funciones cognitivas, como el reconocimiento de patrones y el aprendizaje experiencial.

Entre los modelos de redes neuronales , el mapa autoorganizado (SOM) y la teoría de resonancia adaptativa (ART) se utilizan comúnmente en algoritmos de aprendizaje no supervisado. El SOM es una organización topográfica en la que las ubicaciones cercanas en el mapa representan entradas con propiedades similares. El modelo ART permite que la cantidad de grupos varíe con el tamaño del problema y permite al usuario controlar el grado de similitud entre los miembros de los mismos grupos por medio de una constante definida por el usuario llamada parámetro de vigilancia. Las redes ART se utilizan para muchas tareas de reconocimiento de patrones, como el reconocimiento automático de objetivos y el procesamiento de señales sísmicas. ^[10]

Métodos probabilísticos

Dos de los principales métodos utilizados en el aprendizaje no supervisado son el análisis de componentes principales y el análisis de conglomerados . El análisis de conglomerados se utiliza en el aprendizaje no supervisado para agrupar o segmentar conjuntos de datos con atributos compartidos con el fin de extrapolar relaciones algorítmicas. ^[11] El análisis de conglomerados es una rama del aprendizaje automático que agrupa los datos que no han sido etiquetados , clasificados o categorizados. En lugar de responder a la retroalimentación, el análisis de conglomerados identifica puntos en común en los datos y reacciona en función de la presencia o ausencia de dichos puntos en común en cada nuevo dato. Este enfoque ayuda a detectar puntos de datos anómalos que no encajan en ninguno de los grupos.

Una aplicación central del aprendizaje no supervisado es en el campo de la estimación de densidad en estadística , ^[12] aunque el aprendizaje no supervisado abarca muchos otros dominios que implican resumir y explicar características de datos. Se puede contrastar con el aprendizaje supervisado diciendo que mientras que el aprendizaje supervisado intenta inferir una distribución de probabilidad condicional condicionada a la etiqueta de los datos de entrada; el aprendizaje no supervisado intenta inferir una distribución de probabilidad a priori .

Aproches

Algunos de los algoritmos más comunes utilizados en el aprendizaje no supervisado incluyen: (1) Agrupamiento, (2) Detección de anomalías, (3) Enfoques para el aprendizaje de modelos de variables latentes. Cada enfoque utiliza varios métodos, como se indica a continuación:

Los métodos de agrupamiento incluyen: agrupamiento jerárquico , ^[13] k-medias , ^[14] modelos de mezcla , agrupamiento basado en modelos , DBSCAN y algoritmo OPTICS.
Los métodos de detección de anomalías incluyen: factor de valor atípico local y bosque de aislamiento.
Enfoques para el aprendizaje de modelos de variables latentes como el algoritmo de expectativa-maximización (EM), el método de momentos y las técnicas de separación de señales ciegas ( análisis de componentes principales , análisis de componentes independientes , factorización de matrices no negativas , descomposición en valores singulares ).

Método de momentos

Uno de los enfoques estadísticos para el aprendizaje no supervisado es el método de los momentos . En el método de los momentos, los parámetros desconocidos (de interés) en el modelo están relacionados con los momentos de una o más variables aleatorias y, por lo tanto, estos parámetros desconocidos se pueden estimar dados los momentos. Los momentos generalmente se estiman a partir de muestras de manera empírica. Los momentos básicos son los momentos de primer y segundo orden. Para un vector aleatorio, el momento de primer orden es el vector medio y el momento de segundo orden es la matriz de covarianza (cuando la media es cero). Los momentos de orden superior generalmente se representan utilizando tensores que son la generalización de matrices a órdenes superiores como matrices multidimensionales.

En particular, se ha demostrado que el método de momentos es eficaz para aprender los parámetros de los modelos de variables latentes . Los modelos de variables latentes son modelos estadísticos en los que, además de las variables observadas, también existe un conjunto de variables latentes que no se observan. Un ejemplo muy práctico de modelos de variables latentes en el aprendizaje automático es el modelado de temas , que es un modelo estadístico para generar las palabras (variables observadas) en el documento en función del tema (variable latente) del documento. En el modelado de temas, las palabras del documento se generan de acuerdo con diferentes parámetros estadísticos cuando se cambia el tema del documento. Se ha demostrado que el método de momentos (técnicas de descomposición tensorial) recupera de forma consistente los parámetros de una gran clase de modelos de variables latentes bajo ciertas suposiciones. ^[15]

El algoritmo de expectativa-maximización (EM) es también uno de los métodos más prácticos para aprender modelos de variables latentes. Sin embargo, puede quedarse atascado en óptimos locales y no está garantizado que el algoritmo converja a los verdaderos parámetros desconocidos del modelo. En cambio, en el caso del método de momentos, la convergencia global está garantizada bajo ciertas condiciones.

Véase también

Referencias

^ Wu, Wei. "Aprendizaje no supervisado" (PDF) . Archivado (PDF) del original el 14 de abril de 2024. Consultado el 26 de abril de 2024 .
^ Liu, Xiao; Zhang, Fanjin; Hou, Zhenyu; Mian, Li; Wang, Zhaoyu; Zhang, Jing; Tang, Jie (2021). "Aprendizaje autosupervisado: generativo o contrastivo". Transacciones IEEE sobre conocimiento e ingeniería de datos : 1. arXiv : 2006.08218 . doi :10.1109/TKDE.2021.3090866. ISSN 1041-4347.
^ Radford, Alec; Narasimhan, Karthik; Salimans, Tim; Sutskever, Ilya (11 de junio de 2018). "Mejorar la comprensión del lenguaje mediante el preentrenamiento generativo" (PDF) . OpenAI . pág. 12. Archivado (PDF) del original el 26 de enero de 2021 . Consultado el 23 de enero de 2021 .
^ Li, Zhuohan; Wallace, Eric; Shen, Sheng; Lin, Kevin; Keutzer, Kurt; Klein, Dan; Gonzalez, Joey (21 de noviembre de 2020). "Entrenar a lo grande, luego comprimir: replanteando el tamaño del modelo para un entrenamiento y una inferencia eficientes de los transformadores". Actas de la 37.ª Conferencia internacional sobre aprendizaje automático . PMLR: 5958–5968.
^ Hinton, G. (2012). "Una guía práctica para entrenar máquinas de Boltzmann restringidas" (PDF) . Redes neuronales: trucos del oficio . Apuntes de clase en informática. Vol. 7700. Springer. págs. 599–619. doi :10.1007/978-3-642-35289-8_32. ISBN. 978-3-642-35289-8. Archivado (PDF) del original el 3 de septiembre de 2022. Consultado el 3 de noviembre de 2022 .
^ "Redes de creencias profundas" (video). Septiembre de 2009. Archivado desde el original el 8 de marzo de 2022. Consultado el 27 de marzo de 2022 . {{cite web}}: Parámetro desconocido |people=ignorado ( ayuda )
^ Peter, Dayan ; Hinton, Geoffrey E. ; Neal, Radford M. ; Zemel, Richard S. (1995). "La máquina de Helmholtz". Computación neuronal . 7 (5): 889–904. doi :10.1162/neco.1995.7.5.889. hdl : 21.11116/0000-0002-D6D3-E . PMID 7584891. S2CID 1890561.
^ Buhmann, J.; Kuhnel, H. (1992). "Agrupamiento de datos supervisado y no supervisado con redes neuronales competitivas". [Actas 1992] IJCNN International Joint Conference on Neural Networks . Vol. 4. IEEE. págs. 796–801. doi :10.1109/ijcnn.1992.227220. ISBN 0780305590.S2CID62651220 .
^ Comesaña-Campos, Alberto; Bouza-Rodríguez, José Benito (junio de 2016). "Una aplicación del aprendizaje hebbiano en la toma de decisiones del proceso de diseño". Revista de fabricación inteligente . 27 (3): 487–506. doi :10.1007/s10845-014-0881-z. ISSN 0956-5515. S2CID 207171436.
^ Carpenter, GA y Grossberg, S. (1988). "El arte del reconocimiento adaptativo de patrones por una red neuronal autoorganizada" (PDF) . Computer . 21 (3): 77–88. doi :10.1109/2.33. S2CID 14625094. Archivado desde el original (PDF) el 2018-05-16 . Consultado el 2013-09-16 .
^ Roman, Victor (21 de abril de 2019). "Aprendizaje automático no supervisado: análisis de agrupamiento". Medium . Archivado desde el original el 21 de agosto de 2020. Consultado el 1 de octubre de 2019 .
^ Jordan, Michael I.; Bishop, Christopher M. (2004). "7. Sistemas inteligentes § Redes neuronales". En Tucker, Allen B. (ed.). Manual de informática (2.ª ed.). Chapman & Hall/CRC Press. doi :10.1201/9780203494455. ISBN 1-58488-360-XArchivado desde el original el 3 de noviembre de 2022. Consultado el 3 de noviembre de 2022 .
^ Hastie, Tibshirani y Friedman 2009, págs. 485-586
^ Garbade, Dr Michael J. (12 de septiembre de 2018). "Comprensión de la agrupación en clústeres de K-means en el aprendizaje automático". Medium . Archivado desde el original el 28 de mayo de 2019 . Consultado el 31 de octubre de 2019 .
^ Anandkumar, Animashree; Ge, Rong; Hsu, Daniel; Kakade, Sham; Telgarsky, Matus (2014). "Descomposiciones tensoriales para el aprendizaje de modelos de variables latentes" (PDF) . Journal of Machine Learning Research . 15 : 2773–2832. arXiv : 1210.7559 . Código Bibliográfico :2012arXiv1210.7559A. Archivado (PDF) desde el original el 20 de marzo de 2015 . Consultado el 10 de abril de 2015 .

Lectura adicional

Bousquet, O.; von Luxburg, U .; Raetsch, G., eds. (2004). Conferencias avanzadas sobre aprendizaje automático. Saltador. ISBN 978-3540231226.
Duda, Richard O .; Hart, Peter E .; Stork, David G. (2001). "Aprendizaje no supervisado y agrupamiento". Clasificación de patrones (2.ª ed.). Wiley. ISBN 0-471-05669-3.
Hastie, Trevor ; Tibshirani, Robert ; Friedman, Jerome (2009). "Aprendizaje no supervisado". Los elementos del aprendizaje estadístico: minería de datos, inferencia y predicción . Springer. págs. 485–586. doi :10.1007/978-0-387-84858-7_14. ISBN 978-0-387-84857-0Archivado desde el original el 3 de noviembre de 2022. Consultado el 3 de noviembre de 2022 .
Hinton, Geoffrey ; Sejnowski, Terrence J. , eds. (1999). Aprendizaje no supervisado: fundamentos de la computación neuronal . MIT Press . ISBN 0-262-58168-X.