La teoría de resonancia adaptativa ( ART ) es una teoría desarrollada por Stephen Grossberg y Gail Carpenter sobre aspectos de cómo el cerebro procesa la información . Describe una serie de modelos de redes neuronales artificiales que utilizan métodos de aprendizaje supervisados y no supervisados y abordan problemas como el reconocimiento y la predicción de patrones .
La intuición primaria detrás del modelo ART es que la identificación y el reconocimiento de objetos generalmente ocurren como resultado de la interacción de las expectativas del observador "de arriba hacia abajo" con la información sensorial "de abajo hacia arriba" . El modelo postula que las expectativas "de arriba hacia abajo" toman la forma de una plantilla o prototipo de memoria que luego se compara con las características reales de un objeto tal como lo detectan los sentidos. Esta comparación da lugar a una medida de pertenencia a la categoría. Siempre que esta diferencia entre sensación y expectativa no exceda un umbral establecido llamado "parámetro de vigilancia", el objeto detectado se considerará un miembro de la clase esperada. El sistema ofrece así una solución al problema de "plasticidad/estabilidad", es decir, el problema de adquirir nuevos conocimientos sin alterar el conocimiento existente, lo que también se denomina aprendizaje incremental .

El sistema ART básico es un modelo de aprendizaje no supervisado . Normalmente consta de un campo de comparación y un campo de reconocimiento compuestos por neuronas , un parámetro de vigilancia (umbral de reconocimiento) y un módulo de reinicio .
Existen dos métodos básicos para entrenar redes neuronales basadas en ART: lento y rápido. En el método de aprendizaje lento, el grado de entrenamiento de los pesos de la neurona de reconocimiento con respecto al vector de entrada se calcula con valores continuos mediante ecuaciones diferenciales y, por lo tanto, depende del tiempo durante el cual se presenta el vector de entrada. Con el aprendizaje rápido, se utilizan ecuaciones algebraicas para calcular el grado de ajuste de los pesos que se deben realizar y se utilizan valores binarios. Si bien el aprendizaje rápido es eficaz y eficiente para una variedad de tareas, el método de aprendizaje lento es biológicamente más plausible y se puede utilizar con redes de tiempo continuo (es decir, cuando el vector de entrada puede variar continuamente).
ART 1 [1] [2] es la variedad más simple de redes ART, que solo acepta entradas binarias. ART 2 [3] extiende las capacidades de la red para admitir entradas continuas. ART 2-A [4] es una forma optimizada de ART-2 con un tiempo de ejecución drásticamente acelerado y con resultados cualitativos que solo rara vez son inferiores a la implementación completa de ART-2. ART 3 [5] se basa en ART-2 al simular la regulación rudimentaria de la actividad sináptica por neurotransmisores al incorporar concentraciones simuladas de iones de sodio (Na+) y calcio (Ca2+) en las ecuaciones del sistema, lo que da como resultado un medio fisiológicamente más realista de inhibir parcialmente las categorías que desencadenan restablecimientos de desajustes.
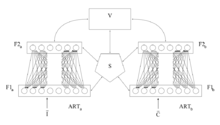
ARTMAP [6] también conocido como ART predictivo , combina dos unidades ART-1 o ART-2 ligeramente modificadas en una estructura de aprendizaje supervisado donde la primera unidad toma los datos de entrada y la segunda unidad toma los datos de salida correctos, que luego se utilizan para realizar el mínimo ajuste posible del parámetro de vigilancia en la primera unidad para realizar la clasificación correcta.
Fuzzy ART [7] implementa lógica difusa en el reconocimiento de patrones de ART, mejorando así la generalización. Una característica opcional (y muy útil) de Fuzzy ART es la codificación complementaria, un medio para incorporar la ausencia de características en las clasificaciones de patrones, lo que ayuda mucho a prevenir la proliferación de categorías ineficiente e innecesaria. Las medidas de similitud aplicadas se basan en la norma L1 . Se sabe que Fuzzy ART es muy sensible al ruido.
Fuzzy ARTMAP [8] es simplemente ARTMAP que utiliza unidades ART difusas, lo que da como resultado un aumento correspondiente en la eficacia.
El ARTMAP difuso simplificado (SFAM) [9] constituye una variante fuertemente simplificada del ARTMAP difuso dedicada a tareas de clasificación .
Gaussian ART [10] y Gaussian ARTMAP [10] utilizan funciones de activación gaussianas y cálculos basados en la teoría de la probabilidad. Por lo tanto, tienen cierta similitud con los modelos de mezcla gaussiana . En comparación con el ART difuso y el ARTMAP difuso, son menos sensibles al ruido. Pero la estabilidad de las representaciones aprendidas se reduce, lo que puede conducir a la proliferación de categorías en tareas de aprendizaje abiertas.
Fusion ART y las redes relacionadas [11] [12] [13] extienden ART y ARTMAP a múltiples canales de patrones. Admiten varios paradigmas de aprendizaje, incluidos el aprendizaje no supervisado, el aprendizaje supervisado y el aprendizaje de refuerzo.
TopoART [14] combina el ART difuso con redes de aprendizaje de topología como el gas neuronal creciente . Además, agrega un mecanismo de reducción de ruido. Existen varias redes neuronales derivadas que extienden TopoART a otros paradigmas de aprendizaje.
Hypersphere ART [15] e Hypersphere ARTMAP [15] están estrechamente relacionados con el ART difuso y el ARTMAP difuso, respectivamente. Pero como utilizan un tipo diferente de representación de categorías (es decir, hiperesferas), no requieren que su entrada se normalice al intervalo [0, 1]. Aplican medidas de similitud basadas en la norma L2 .
LAPART [16] Las redes neuronales de la teoría de resonancia adaptativa con cebadores laterales (LAPART) acoplan dos algoritmos de ART difusos para crear un mecanismo para realizar predicciones basadas en asociaciones aprendidas. El acoplamiento de los dos ART difusos tiene una estabilidad única que permite que el sistema converja rápidamente hacia una solución clara. Además, puede realizar inferencia lógica y aprendizaje supervisado similar al ARTMAP difuso.
Se ha observado que los resultados de Fuzzy ART y ART 1 (es decir, las categorías aprendidas) dependen críticamente del orden en el que se procesan los datos de entrenamiento. El efecto se puede reducir hasta cierto punto utilizando una tasa de aprendizaje más lenta, pero está presente independientemente del tamaño del conjunto de datos de entrada. Por lo tanto, las estimaciones de Fuzzy ART y ART 1 no poseen la propiedad estadística de consistencia . [17] Este problema puede considerarse como un efecto secundario de los respectivos mecanismos que garantizan un aprendizaje estable en ambas redes.
Las redes ART más avanzadas, como TopoART y Hypersphere TopoART, que resumen las categorías en grupos, pueden resolver este problema, ya que las formas de los grupos no dependen del orden de creación de las categorías asociadas (cf. Fig. 3(g, h) y Fig. 4 de [18] ).
Wasserman, Philip D. (1989), Computación neuronal: teoría y práctica, Nueva York: Van Nostrand Reinhold, ISBN 0-442-20743-3