Los modelos de aguas subterráneas son modelos informáticos de los sistemas de flujo de aguas subterráneas y son utilizados por hidrólogos e hidrogeólogos . Los modelos de aguas subterráneas se utilizan para simular y predecir las condiciones de los acuíferos .

Es difícil dar una definición inequívoca de "modelo de aguas subterráneas", pero hay muchas características comunes.
Un modelo de aguas subterráneas puede ser un modelo a escala o un modelo eléctrico de una situación de aguas subterráneas o de un acuífero . Los modelos de aguas subterráneas se utilizan para representar el flujo natural de aguas subterráneas en el medio ambiente. Algunos modelos de aguas subterráneas incluyen aspectos de calidad (química) de las aguas subterráneas. Dichos modelos de aguas subterráneas intentan predecir el destino y el movimiento de las sustancias químicas en un escenario natural, urbano o hipotético.
Los modelos de aguas subterráneas se pueden utilizar para predecir los efectos de los cambios hidrológicos (como el bombeo de agua subterránea o los desarrollos de irrigación) en el comportamiento del acuífero y a menudo se los denomina modelos de simulación de aguas subterráneas. Los modelos de aguas subterráneas se utilizan en diversos planes de gestión del agua para áreas urbanas.
Como los cálculos en los modelos matemáticos de aguas subterráneas se basan en ecuaciones de flujo de aguas subterráneas , que son ecuaciones diferenciales que a menudo solo se pueden resolver mediante métodos aproximados utilizando un análisis numérico , estos modelos también se denominan modelos matemáticos, numéricos o computacionales de aguas subterráneas . [1]
Los modelos matemáticos o numéricos suelen basarse en la física real que sigue el flujo de las aguas subterráneas. Estas ecuaciones matemáticas se resuelven utilizando códigos numéricos como MODFLOW , ParFlow, HydroGeoSphere , OpenGeoSys, etc. En el artículo sobre " Hidrogeología " se analizan diversos tipos de soluciones numéricas, como el método de diferencias finitas y el método de elementos finitos .
Para los cálculos se necesitan datos como:
El modelo puede tener componentes químicos como salinidad del agua , salinidad del suelo y otros indicadores de calidad del agua y del suelo, para los cuales también pueden necesitarse insumos.

El acoplamiento primario entre el agua subterránea y los aportes hidrológicos es la zona no saturada o zona vadosa . El suelo actúa para dividir los aportes hidrológicos, como la lluvia o el deshielo, en escorrentía superficial , humedad del suelo , evapotranspiración y recarga de agua subterránea . Los flujos a través de la zona no saturada que acoplan el agua superficial a la humedad del suelo y el agua subterránea pueden ser ascendentes o descendentes, dependiendo del gradiente de carga hidráulica en el suelo, y se pueden modelar utilizando la solución numérica de la ecuación de Richards [2] , la ecuación diferencial parcial o la ecuación diferencial ordinaria, el método de contenido de agua finito [3], tal como se validó para modelar las interacciones de las aguas subterráneas y la zona vadosa . [4]
Los insumos operacionales se refieren a las interferencias humanas en la gestión del agua, como el riego , el drenaje , el bombeo de pozos , el control del nivel freático y el funcionamiento de las cuencas de retención o infiltración , que a menudo son de naturaleza hidrológica.
Estos insumos también pueden variar en el tiempo y el espacio.
Se realizan muchos modelos de aguas subterráneas con el propósito de evaluar los efectos de las medidas de ingeniería hidráulica .

Las condiciones de contorno pueden estar relacionadas con los niveles del nivel freático , las presiones artesianas y la carga hidráulica a lo largo de los límites del modelo por un lado ( condiciones de carga ) o con las entradas y salidas de agua subterránea a lo largo de los límites del modelo por el otro lado ( condiciones de flujo ). Esto también puede incluir aspectos de calidad del agua como la salinidad.
Las condiciones iniciales se refieren a valores iniciales de elementos que pueden aumentar o disminuir a lo largo del tiempo dentro del dominio del modelo y cubren en gran medida los mismos fenómenos que las condiciones de límite.
Las condiciones iniciales y de contorno pueden variar de un lugar a otro. Las condiciones de contorno pueden mantenerse constantes o ser variables en el tiempo.
.JPG/440px-File-Saltmod8_(2).JPG)
Los parámetros generalmente se refieren a la geometría y las distancias en el dominio a modelar y a aquellas propiedades físicas del acuífero que son más o menos constantes en el tiempo pero que pueden ser variables en el espacio.
Los parámetros importantes son la topografía , el espesor de las capas de suelo/roca y su conductividad hidráulica horizontal/vertical (permeabilidad al agua), la transmisividad y resistencia del acuífero , la porosidad del acuífero y el coeficiente de almacenamiento , así como la capilaridad de la zona no saturada. Para más detalles, consulte el artículo sobre hidrogeología .
Algunos parámetros pueden verse influidos por cambios en la situación de las aguas subterráneas, como el espesor de una capa de suelo que puede reducirse cuando el nivel freático desciende y/o se reduce la presión hidráulica. Este fenómeno se denomina subsidencia . El espesor, en este caso, es variable en el tiempo y no es un parámetro propiamente dicho.
La aplicabilidad de un modelo de aguas subterráneas a una situación real depende de la precisión de los datos de entrada y de los parámetros . La determinación de estos requiere un estudio considerable, como la recopilación de datos hidrológicos ( lluvia , evapotranspiración , riego , drenaje ) y la determinación de los parámetros mencionados anteriormente, incluidas las pruebas de bombeo . Como muchos parámetros son bastante variables en el espacio, se necesita el juicio de expertos para llegar a valores representativos.
Los modelos también pueden utilizarse para el análisis if-then : si el valor de un parámetro es A, ¿cuál es el resultado?, y si el valor del parámetro es B, ¿cuál es la influencia? Este análisis puede ser suficiente para obtener una impresión aproximada del comportamiento de las aguas subterráneas, pero también puede servir para hacer un análisis de sensibilidad para responder a la pregunta: ¿qué factores tienen una gran influencia y cuáles tienen una influencia menor? Con tal información se pueden dirigir los esfuerzos de investigación más hacia los factores influyentes.
Cuando se han reunido suficientes datos, es posible determinar parte de la información faltante mediante calibración . Esto implica que se supone un rango de valores para el valor desconocido o dudoso de un determinado parámetro y se ejecuta el modelo repetidamente mientras se comparan los resultados con los datos correspondientes conocidos. Por ejemplo, si se dispone de cifras de salinidad del agua subterránea y el valor de la conductividad hidráulica es incierto, se supone un rango de conductividades y se selecciona ese valor de conductividad como "verdadero" que produce resultados de salinidad cercanos a los valores observados, lo que significa que el flujo de agua subterránea, tal como se rige por la conductividad hidráulica, está de acuerdo con las condiciones de salinidad. Este procedimiento es similar a la medición del flujo en un río o canal al dejar que agua muy salina de una concentración de sal conocida gotee en el canal y se mide la concentración de sal resultante aguas abajo.
Los modelos de aguas subterráneas pueden ser unidimensionales, bidimensionales, tridimensionales y semitridimensionales. Los modelos bidimensionales y tridimensionales pueden tener en cuenta la anisotropía del acuífero con respecto a la conductividad hidráulica , es decir, esta propiedad puede variar en diferentes direcciones.


En los modelos semitridimensionales, el flujo horizontal se describe mediante ecuaciones de flujo bidimensionales (es decir, en la dirección horizontal x e y). Los flujos verticales (en la dirección z) se describen (a) con una ecuación de flujo unidimensional, o (b) se derivan de un balance hídrico de flujos horizontales que convierte el exceso de agua subterránea entrante horizontalmente sobre el agua subterránea saliente horizontalmente en flujo vertical bajo el supuesto de que el agua es incompresible .
Hay dos clases de modelos semi tridimensionales:
Un ejemplo de un modelo radial no discretizado es la descripción del flujo de agua subterránea que se mueve radialmente hacia un pozo profundo en una red de pozos de los cuales se extrae agua. [7] El flujo radial pasa a través de una sección transversal cilíndrica vertical que representa el equipotencial hidráulico cuya superficie disminuye en la dirección del eje de intersección de los planos radiales donde se ubica el pozo.

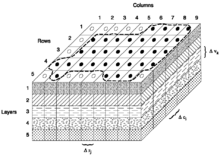
Los modelos prismáticos discretizados como SahysMod [8] tienen una cuadrícula sobre la superficie terrestre solamente. La red de cuadrícula bidimensional consta de triángulos, cuadrados, rectángulos o polígonos . Por lo tanto, el dominio de flujo se subdivide en bloques verticales o prismas . Los prismas se pueden discretizar en capas horizontales con diferentes características que también pueden variar entre los prismas. El flujo de agua subterránea entre prismas vecinos se calcula utilizando ecuaciones de flujo de agua subterránea horizontal bidimensional. Los flujos verticales se encuentran aplicando ecuaciones de flujo unidimensionales en sentido vertical, o pueden derivarse del balance hídrico: el exceso de entrada horizontal sobre la salida horizontal (o viceversa) se traduce en flujo vertical, como se demuestra en el artículo Hidrología (agricultura) .
En los modelos semitridimensionales, el flujo intermedio entre el horizontal y el vertical no se modela como en los modelos verdaderamente tridimensionales. Sin embargo, al igual que los modelos verdaderamente tridimensionales, estos modelos sí permiten la introducción de sistemas de drenaje subterráneo horizontales y verticales .
Los acuíferos semiconfinados con una capa lentamente permeable que recubre el acuífero (el acuitardo ) se pueden incluir en el modelo simulando el flujo vertical a través de él bajo la influencia de una sobrepresión en el acuífero propiamente dicho en relación con el nivel del nivel freático dentro o por encima del acuitardo.