En matemáticas , se dice que una función de valor real f en el intervalo [ a , b ] es singular si tiene las siguientes propiedades:
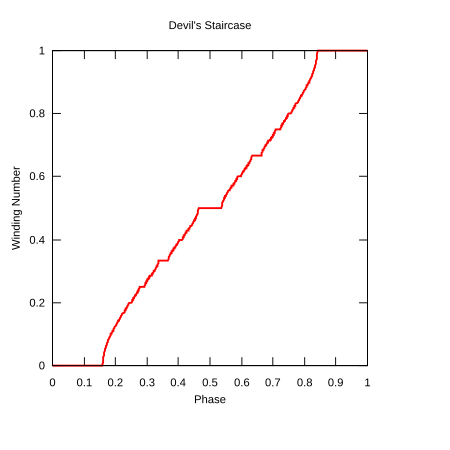
Un ejemplo estándar de una función singular es la función de Cantor , que a veces se denomina la escalera del diablo (un término que también se utiliza para las funciones singulares en general). Sin embargo, existen otras funciones a las que se les ha dado ese nombre. Una de ellas se define en términos de la función circular .
Si f ( x ) = 0 para todo x ≤ a y f ( x ) = 1 para todo x ≥ b , entonces la función puede tomarse para representar una función de distribución acumulativa para una variable aleatoria que no es una variable aleatoria discreta (ya que la probabilidad es cero para cada punto) ni una variable aleatoria absolutamente continua (ya que la densidad de probabilidad es cero en todos los lugares donde existe).
Las funciones singulares se dan, por ejemplo, como secuencias de fases o estructuras moduladas espacialmente en sólidos e imanes , descritas de manera prototípica por el modelo de Frenkel-Kontorova y por el modelo ANNNI , así como en algunos sistemas dinámicos . El caso más famoso, quizás, es que se encuentran en el centro del efecto Hall cuántico fraccionario .
Cuando se habla de análisis matemático en general, o más específicamente de análisis real o análisis complejo o ecuaciones diferenciales , es común que una función que contiene una singularidad matemática se denomine "función singular". Esto es especialmente cierto cuando se hace referencia a funciones que divergen al infinito en un punto o en un límite. Por ejemplo, se podría decir: " 1/x se vuelve singular en el origen, por lo que 1/x es una función singular".
En la materia denominada análisis distribucional o generalizado de funciones se han desarrollado técnicas avanzadas para trabajar con funciones que contienen singularidades . Se define una derivada débil que permite utilizar funciones singulares en ecuaciones diferenciales parciales , etc.
(**) Esta condición depende de las referencias [1]