Función de cantor

Función continua que no es absolutamente continua

La gráfica de la función de Cantor en el intervalo unitario

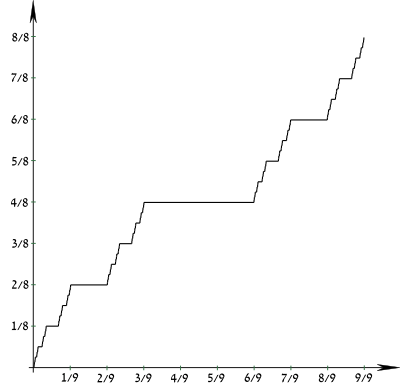
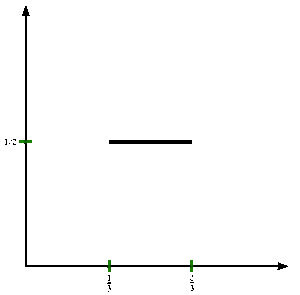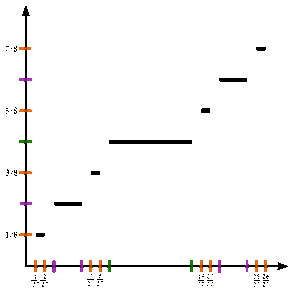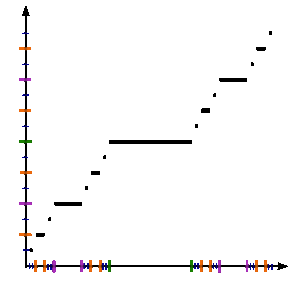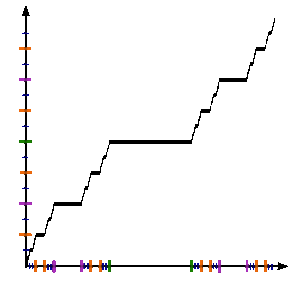
En matemáticas , la función de Cantor es un ejemplo de una función que es continua , pero no absolutamente continua . Es un contraejemplo notorio en el análisis, porque desafía las intuiciones ingenuas sobre continuidad, derivada y medida . Aunque es continua en todas partes y tiene derivada cero en casi todas partes, su valor todavía va de 0 a 1 cuando su argumento va de 0 a 1. Por lo tanto, en un sentido la función parece muy parecida a una constante que no puede crecer, y en otro, de hecho crece de manera monótona .

También se le llama función ternaria de Cantor , función de Lebesgue , ^[1] función singular de Lebesgue , función de Cantor-Vitali , escalera del Diablo , ^[2] función de escalera de Cantor , ^[3] y función de Cantor-Lebesgue . ^[4] Georg Cantor  (1884) introdujo la función de Cantor y mencionó que Scheeffer señaló que era un contraejemplo de una extensión del teorema fundamental del cálculo reclamado por Harnack . La función de Cantor fue discutida y popularizada por Scheeffer (1884), Lebesgue (1904) y Vitali (1905).

Definición

Construcción iterada de la función de Cantor

Para definir la función de Cantor , sea cualquier número en y obtenga mediante los siguientes pasos: ${\displaystyle c:[0,1]\to [0,1]}$ ${\displaystyle x}$ ${\displaystyle [0,1]}$ ${\displaystyle c(x)}$

1. Expresar en base 3, utilizando los dígitos 0, 1, 2. ${\displaystyle x}$
2. Si la representación en base 3 de contiene un 1, reemplace cada dígito estrictamente después del primer 1 con 0. ${\displaystyle x}$
3. Reemplace los 2 restantes por 1.
4. Interprete el resultado como un número binario. El resultado es . ${\displaystyle c(x)}$

Por ejemplo:

• ${\displaystyle {\tfrac {1}{4}}}$tiene la representación ternaria 0.02020202... No hay 1, por lo que la siguiente etapa sigue siendo 0.02020202... Esto se reescribe como 0.01010101... Esta es la representación binaria de , por lo que . ${\displaystyle {\tfrac {1}{3}}}$ ${\displaystyle c({\tfrac {1}{4}})={\tfrac {1}{3}}}$
• ${\displaystyle {\tfrac {1}{5}}}$tiene la representación ternaria 0.01210121... Los dígitos después del primer 1 se reemplazan por 0 para producir 0.01000000... Esto no se reescribe ya que no tiene 2. Esta es la representación binaria de , por lo tanto . ${\displaystyle {\tfrac {1}{4}}}$ ${\displaystyle c({\tfrac {1}{5}})={\tfrac {1}{4}}}$
• ${\displaystyle {\tfrac {200}{243}}}$tiene la representación ternaria 0,21102 (o 0,211012222...). Los dígitos después del primer 1 se reemplazan por 0 para producir 0,21. Esto se reescribe como 0,11. Esta es la representación binaria de , por lo tanto . ${\displaystyle {\tfrac {3}{4}}}$ ${\displaystyle c({\tfrac {200}{243}})={\tfrac {3}{4}}}$

De manera equivalente, si el conjunto de Cantor está en [0,1], entonces la función de Cantor se puede definir como ${\displaystyle {\mathcal {C}}}$ ${\displaystyle c:[0,1]\to [0,1]}$

${\displaystyle c(x)={\begin{cases}\sum _{n=1}^{\infty }{\frac {a_{n}}{2^{n}}},&x=\sum _{n=1}^{\infty }{\frac {2a_{n}}{3^{n}}}\in {\mathcal {C}}\ \mathrm {for} \ a_{n}\in \{0,1\};\\\sup _{y\leq x,\,y\in {\mathcal {C}}}c(y),&x\in [0,1]\smallsetminus {\mathcal {C}}.\end{cases}}}$

Esta fórmula está bien definida, ya que cada miembro del conjunto de Cantor tiene una representación única en base 3 que solo contiene los dígitos 0 o 2. (Para algunos miembros de , la expansión ternaria se repite con 2 finales y hay una expansión alternativa no repetitiva que termina en 1. Por ejemplo, = 0,1 ₃ = 0,02222... ₃ es un miembro del conjunto de Cantor). Dado que y , y es monótono en , está claro que también se cumple para todos los . ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\tfrac {1}{3}}}$ ${\displaystyle c(0)=0}$ ${\displaystyle c(1)=1}$ ${\displaystyle c}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle 0\leq c(x)\leq 1}$ ${\displaystyle x\in [0,1]\smallsetminus {\mathcal {C}}}$

Propiedades

La función de Cantor desafía las intuiciones ingenuas sobre continuidad y medida ; aunque es continua en todas partes y tiene derivada cero en casi todas partes , va de 0 a 1 como va de 0 a 1, y toma todos los valores intermedios. La función de Cantor es el ejemplo más frecuentemente citado de una función real que es uniformemente continua (precisamente, es continua de Hölder de exponente α  = log 2/log 3) pero no absolutamente continua . Es constante en intervalos de la forma (0. x ₁ x ₂ x ₃ ... x _n 022222..., 0. x ₁ x ₂ x ₃ ... x _n 200000...), y cada punto que no está en el conjunto de Cantor está en uno de estos intervalos, por lo que su derivada es 0 fuera del conjunto de Cantor. Por otro lado, no tiene derivada en ningún punto en un subconjunto incontable del conjunto de Cantor que contenga los puntos finales del intervalo descritos anteriormente. ${\textstyle c(x)}$ ${\textstyle x}$

La función de Cantor también puede verse como la función de distribución de probabilidad acumulada de la medida de Bernoulli 1/2-1/2 μ apoyada en el conjunto de Cantor: . Esta distribución de probabilidad, llamada distribución de Cantor , no tiene parte discreta. Es decir, la medida correspondiente no tiene átomos . Es por eso que no hay discontinuidades de salto en la función; cualquier salto de ese tipo correspondería a un átomo en la medida. ${\textstyle c(x)=\mu ([0,x])}$

Sin embargo, ninguna parte no constante de la función de Cantor puede representarse como una integral de una función de densidad de probabilidad ; la integración de cualquier función de densidad de probabilidad putativa que no sea casi en todas partes cero en cualquier intervalo dará una probabilidad positiva en algún intervalo al que esta distribución asigna probabilidad cero. En particular, como señaló Vitali (1905), la función no es la integral de su derivada aunque la derivada exista casi en todas partes.

La función de Cantor es el ejemplo estándar de una función singular .

La función de Cantor también es un ejemplo estándar de función con variación acotada , pero, como se mencionó anteriormente, no es absolutamente continua. Sin embargo, toda función absolutamente continua es continua con variación acotada.

La función de Cantor no es decreciente y, por lo tanto, en particular, su gráfica define una curva rectificable . Scheeffer (1884) demostró que la longitud de arco de su gráfica es 2. Nótese que la gráfica de cualquier función no decreciente tal que y tiene una longitud no mayor que 2. En este sentido, la función de Cantor es extremal. ${\displaystyle f(0)=0}$ ${\displaystyle f(1)=1}$

Falta de continuidad absoluta

Como la medida de Lebesgue del conjunto de Cantor incontablemente infinito es 0, para cualquier ε  < 1 y δ positivo , existe una secuencia finita de subintervalos  disjuntos por pares con longitud total < δ sobre los cuales la función de Cantor aumenta acumulativamente más que  ε .

De hecho, para cada δ  > 0 hay un número finito de intervalos disjuntos por pares ( x _k , y _k ) (1 ≤  k  ≤  M ) con y . ${\displaystyle \sum \limits _{k=1}^{M}(y_{k}-x_{k})<\delta }$ ${\displaystyle \sum \limits _{k=1}^{M}(c(y_{k})-c(x_{k}))=1}$

Definiciones alternativas

Construcción iterativa

A continuación definimos una secuencia { f _n } de funciones en el intervalo unitario que converge a la función de Cantor.

Sea f ₀ ( x ) = x .

Entonces, para cada entero n ≥ 0 , la siguiente función f _{n +1} ( x ) se definirá en términos de f _n ( x ) de la siguiente manera:

Sea f _{n +1} ( x ) = 1/2 × f _n (3 x ) , cuando 0 ≤ x ≤ 1/3  ;

Sea f _{n +1} ( x ) = 1/2, cuando 1/3 ≤ x ≤ 2/3  ;

Sea f _{n +1} ( x ) = 1/2 + 1/2 × f _n (3  x − 2) , cuando 2/3 ≤ x ≤ 1 .

Las tres definiciones son compatibles en los puntos extremos 1/3 y 2/3, porque f _n (0) = 0 y f _n (1) = 1 para cada  n , por inducción. Se puede comprobar que f _n converge puntualmente a la función de Cantor definida anteriormente. Además, la convergencia es uniforme. En efecto, separando en tres casos, según la definición de f _{n +1} , se ve que

${\displaystyle \max _{x\in [0,1]}|f_{n+1}(x)-f_{n}(x)|\leq {\frac {1}{2}}\,\max _{x\in [0,1]}|f_{n}(x)-f_{n-1}(x)|,\quad n\geq 1.}$

Si f denota la función límite, se deduce que, para cada n  ≥ 0,

${\displaystyle \max _{x\in [0,1]}|f(x)-f_{n}(x)|\leq 2^{-n+1}\,\max _{x\in [0,1]}|f_{1}(x)-f_{0}(x)|.}$

Volumen fractal

La función de Cantor está estrechamente relacionada con el conjunto de Cantor . El conjunto de Cantor C puede definirse como el conjunto de aquellos números en el intervalo [0, 1] que no contienen el dígito 1 en su expansión de base 3 (triádica) , excepto si el 1 es seguido solo por ceros (en cuyo caso la cola 1000 puede reemplazarse por 0222 para deshacerse de cualquier 1). Resulta que el conjunto de Cantor es un fractal con (incontablemente) infinitos puntos (volumen de dimensión cero), pero longitud cero (volumen unidimensional). Solo el volumen D -dimensional (en el sentido de una medida de Hausdorff ) toma un valor finito, donde es la dimensión fractal de C. Podemos definir la función de Cantor alternativamente como el volumen D -dimensional de secciones del conjunto de Cantor. ${\displaystyle \ldots }$ ${\displaystyle \ldots }$ ${\displaystyle H_{D}}$ ${\displaystyle D=\log(2)/\log(3)}$

${\displaystyle f(x)=H_{D}(C\cap (0,x)).}$

Autosimilitud

La función de Cantor posee varias simetrías . Para , existe una simetría de reflexión ${\displaystyle 0\leq x\leq 1}$

${\displaystyle c(x)=1-c(1-x)}$

y un par de aumentos, uno a la izquierda y otro a la derecha:

${\displaystyle c\left({\frac {x}{3}}\right)={\frac {c(x)}{2}}}$

y

${\displaystyle c\left({\frac {x+2}{3}}\right)={\frac {1+c(x)}{2}}}$

Las ampliaciones se pueden aplicar en cascada; generan el monoide diádico . Esto se demuestra definiendo varias funciones auxiliares. Defina la reflexión como

${\displaystyle r(x)=1-x}$

La primera autosimetría se puede expresar como

${\displaystyle r\circ c=c\circ r}$

donde el símbolo denota la composición de funciones. Es decir, y lo mismo para los demás casos. Para los aumentos izquierdo y derecho, escriba las asignaciones izquierdas ${\displaystyle \circ }$ ${\displaystyle (r\circ c)(x)=r(c(x))=1-c(x)}$

${\displaystyle L_{D}(x)={\frac {x}{2}}}$y ${\displaystyle L_{C}(x)={\frac {x}{3}}}$

Entonces la función de Cantor obedece

${\displaystyle L_{D}\circ c=c\circ L_{C}}$

De manera similar, defina las asignaciones correctas como

${\displaystyle R_{D}(x)={\frac {1+x}{2}}}$y ${\displaystyle R_{C}(x)={\frac {2+x}{3}}}$

Luego, igualmente,

${\displaystyle R_{D}\circ c=c\circ R_{C}}$

Los dos lados se pueden reflejar uno sobre el otro, de modo que

${\displaystyle L_{D}\circ r=r\circ R_{D}}$

y asimismo,

${\displaystyle L_{C}\circ r=r\circ R_{C}}$

Estas operaciones se pueden apilar de forma arbitraria. Consideremos, por ejemplo, la secuencia de movimientos de izquierda a derecha. Si añadimos los subíndices C y D y, para mayor claridad, omitimos el operador de composición en todos los lugares excepto en unos pocos, tenemos: ${\displaystyle LRLLR.}$ ${\displaystyle \circ }$

${\displaystyle L_{D}R_{D}L_{D}L_{D}R_{D}\circ c=c\circ L_{C}R_{C}L_{C}L_{C}R_{C}}$

Las cadenas arbitrarias de longitud finita en las letras L y R corresponden a los racionales diádicos , en el sentido de que cada racional diádico puede escribirse tanto para los enteros n y m como para una longitud finita de bits con Por lo tanto, cada racional diádico está en correspondencia biunívoca con alguna autosimetría de la función de Cantor. ${\displaystyle y=n/2^{m}}$ ${\displaystyle y=0.b_{1}b_{2}b_{3}\cdots b_{m}}$ ${\displaystyle b_{k}\in \{0,1\}.}$

Algunas reorganizaciones de la notación pueden hacer que lo anterior sea un poco más fácil de expresar. Sea y representan L y R. La composición de funciones extiende esto a un monoide , en el sentido de que se puede escribir y en general, para algunas cadenas binarias de dígitos A , B , donde AB es simplemente la concatenación ordinaria de tales cadenas. El monoide diádico M es entonces el monoide de todos esos movimientos de izquierda a derecha de longitud finita. Escribiéndolo como un elemento general del monoide, existe una autosimetría correspondiente de la función de Cantor: ${\displaystyle g_{0}}$ ${\displaystyle g_{1}}$ ${\displaystyle g_{010}=g_{0}g_{1}g_{0}}$ ${\displaystyle g_{A}g_{B}=g_{AB}}$ ${\displaystyle \gamma \in M}$

${\displaystyle \gamma _{D}\circ c=c\circ \gamma _{C}}$

El monoide diádico tiene varias propiedades interesantes. Puede verse como un número finito de movimientos de izquierda a derecha hacia abajo en un árbol binario infinito ; las "hojas" infinitamente distantes del árbol corresponden a los puntos del conjunto de Cantor y, por lo tanto, el monoide también representa las autosimetrías del conjunto de Cantor. De hecho, una gran clase de fractales que ocurren comúnmente se describen mediante el monoide diádico; se pueden encontrar ejemplos adicionales en el artículo sobre las curvas de De Rham . Otros fractales que poseen autosimilitud se describen con otros tipos de monoides. El monoide diádico es en sí mismo un submonoide del grupo modular. ${\displaystyle SL(2,\mathbb {Z} ).}$

Obsérvese que la función de Cantor tiene más que un parecido pasajero con la función de signo de interrogación de Minkowski . En particular, obedece exactamente a las mismas relaciones de simetría, aunque en una forma modificada.

Generalizaciones

Dejar

${\displaystyle y=\sum _{k=1}^{\infty }b_{k}2^{-k}}$

sea ​​la expansión diádica (binaria) del número real 0 ≤ y ≤ 1 en términos de dígitos binarios b _k ∈ {0,1}. Esta expansión se analiza con mayor detalle en el artículo sobre la transformación diádica . Luego considere la función

${\displaystyle C_{z}(y)=\sum _{k=1}^{\infty }b_{k}z^{k}.}$

Para z  = 1/3, la inversa de la función x = 2  C _1/3 ( y ) es la función de Cantor. Es decir, y  =  y ( x ) es la función de Cantor. En general, para cualquier z  < 1/2, C _z ( y ) parece la función de Cantor girada de lado, con el ancho de los pasos ensanchándose a medida que z se acerca a cero.

Como se mencionó anteriormente, la función de Cantor también es la función de distribución acumulativa de una medida en el conjunto de Cantor. Se pueden obtener diferentes funciones de Cantor, o Escaleras del Diablo, considerando diferentes medidas de probabilidad sin átomos admitidas en el conjunto de Cantor u otros fractales. Si bien la función de Cantor tiene derivada 0 en casi todas partes, la investigación actual se centra en la cuestión del tamaño del conjunto de puntos donde la derivada superior derecha es distinta de la derivada inferior derecha, lo que hace que la derivada no exista. Este análisis de diferenciabilidad generalmente se da en términos de dimensión fractal , siendo la dimensión de Hausdorff la opción más popular. Esta línea de investigación fue iniciada en la década de 1990 por Darst, ^[5] quien demostró que la dimensión de Hausdorff del conjunto de no diferenciabilidad de la función de Cantor es el cuadrado de la dimensión del conjunto de Cantor, . Posteriormente, Falconer ^[6] demostró que esta relación de cuadratura se cumple para todas las medidas regulares y singulares de Ahlfors, es decir, Más tarde, Troscheit ^[7] obtuvo una imagen más completa del conjunto donde la derivada no existe para medidas de Gibbs normalizadas más generales apoyadas en conjuntos autoconformes y autosimilares . ${\displaystyle (\log 2/\log 3)^{2}}$ $${\displaystyle \dim _{H}\left\{x:f'(x)=\lim _{h\to 0^{+}}{\frac {\mu ([x,x+h])}{h}}{\text{ does not exist}}\right\}=\left(\dim _{H}\operatorname {supp} (\mu )\right)^{2}}$$

La función de signo de interrogación de Hermann Minkowski se parece vagamente a la función de Cantor en términos visuales, ya que parece una forma "suavizada" de esta última; se puede construir pasando de una expansión fraccionaria continua a una expansión binaria, de la misma manera que la función de Cantor se puede construir pasando de una expansión ternaria a una expansión binaria. La función de signo de interrogación tiene la interesante propiedad de tener derivadas que se desvanecen en todos los números racionales.

Véase también

• Transformación diádica
• Función de Weierstrass , función que es continua en todas partes pero no diferenciable en ninguna.

Notas

1. Vestrup 2003, Sección 4.6.
2. Thomson, Bruckner y Bruckner 2008, pág. 252.
3. "Función de la Escalera del Cantor".
4. Bass 2013, pág. 28.
5. Darst, Richard (1 de septiembre de 1993). "La dimensión de Hausdorff del conjunto de no diferenciabilidad de la función de Cantor es [ln(2)/ln(3)]2". Actas de la American Mathematical Society . 119 (1): 105–108. doi :10.2307/2159830. JSTOR  2159830.
6. Falconer, Kenneth J. (1 de enero de 2004). "Análisis multifractal unilateral y puntos de no diferenciabilidad de las escaleras del diablo". Actas matemáticas de la Sociedad filosófica de Cambridge . 136 (1): 167–174. Bibcode :2004MPCPS.136..167F. doi :10.1017/S0305004103006960 (inactivo el 1 de noviembre de 2024). ISSN  1469-8064. S2CID  122381614.{{cite journal}}: CS1 maint: DOI inactive as of November 2024 (link)
7. Troscheit, Sascha (1 de marzo de 2014). "Diferenciabilidad de Hölder de las escaleras del diablo autoconformes". Actas matemáticas de la Sociedad filosófica de Cambridge . 156 (2): 295–311. arXiv : 1301.1286 . Código Bibliográfico :2014MPCPS.156..295T. doi :10.1017/S0305004113000698. ISSN  1469-8064. S2CID  56402751.

Referencias

• Bass, Richard Franklin (2013) [2011]. Análisis real para estudiantes de posgrado (segunda edición). Createspace Independent Publishing. ISBN 978-1-4818-6914-0.
• Cantor, G. (1884). "De la puissance des ensembles parfaits de pointes: Extrait d'une lettre adressée à l'éditeur" [El poder de los conjuntos perfectos de puntos: Extracto de una carta dirigida al editor]. Acta Matemática . 4 . Prensa internacional de Boston: 381–392. doi : 10.1007/bf02418423 . ISSN  0001-5962.Reimpreso en: E. Zermelo (Ed.), Gesammelte Abhandlungen Mathematischen und Philosophischen Inhalts, Springer, Nueva York, 1980.
• Darst, Richard B.; Palagallo, Judith A.; Price, Thomas E. (2010), Curvas curiosas , Hackensack, NJ: World Scientific Publishing Co. Pte. Ltd., ISBN 978-981-4291-28-6, Sr.  2681574
• Dovgoshey, O.; Martío, O.; Riazanov, V.; Vuorinen, M. (2006). "La función Cantor". Exposiciones Mathematicae . 24 (1). Elsevier BV: 1–37. doi : 10.1016/j.exmath.2005.05.002. ISSN  0723-0869. SEÑOR  2195181.
• Fleron, Julian F. (1994-04-01). "Una nota sobre la historia del conjunto de Cantor y la función de Cantor". Revista de matemáticas . 67 (2). Informa UK Limited: 136–140. doi :10.2307/2690689. ISSN  0025-570X. JSTOR  2690689.
• Lebesgue, H. (1904), Leçons sur l'intégration et la recherche des fonctionsprimitives [ Lecciones sobre integración y búsqueda de funciones primitivas ], París: Gauthier-Villars
• Leoni, Giovanni (2017). Un primer curso sobre espacios de Sobolev. Vol. 181 (2.ª ed.). Providence, Rhode Island: American Mathematical Society. pág. 734. ISBN 978-1-4704-2921-8.OCLC 976406106  .
• Scheeffer, Ludwig (1884). "Allgemeine Untersuchungen über Rectification der Curven" [Investigaciones generales sobre la rectificación de las curvas]. Acta Matemática . 5 . Prensa internacional de Boston: 49–82. doi : 10.1007/bf02421552 . ISSN  0001-5962.
• Thomson, Brian S.; Bruckner, Judith B.; Bruckner, Andrew M. (2008) [2001]. Análisis real elemental (segunda edición). ClassicalRealAnalysis.com. ISBN 978-1-4348-4367-8.
• Vestrup, EM (2003). La teoría de medidas e integración . Series de Wiley en probabilidad y estadística. John Wiley & sons. ISBN 978-0471249771.
• Vitali, A. (1905), "Sulle funzioni integrali" [Sobre las funciones integrales], Atti Accad. Ciencia. Turín Cl. Ciencia. Fis. Estera. Naturaleza. , 40 : 1021-1034

Enlaces externos

• Función ternaria de Cantor en Enciclopedia de Matemáticas
• Función de Cantor por Douglas Rivers, el Proyecto de Demostraciones Wolfram .
• Weisstein, Eric W. "Función de Cantor". MathWorld .