En matemáticas , el teorema de representación de Birkhoff para redes distributivas establece que los elementos de cualquier red distributiva finita pueden representarse como conjuntos finitos , de tal manera que las operaciones de red corresponden a uniones e intersecciones de conjuntos. Aquí, una red es una estructura abstracta con dos operaciones binarias , las operaciones de "encuentro" y "unión", que deben obedecer ciertos axiomas; es distributiva si estas dos operaciones obedecen a la ley distributiva . Las operaciones de unión e intersección, en una familia de conjuntos que está cerrada bajo estas operaciones, forman automáticamente una red distributiva, y el teorema de representación de Birkhoff establece que toda red distributiva finita puede formarse de esta manera. Recibe su nombre en honor a Garrett Birkhoff , quien publicó una prueba de él en 1937. [1]
El teorema puede interpretarse como una correspondencia biunívoca entre redes distributivas y órdenes parciales , entre espacios de conocimiento cuasiordinales y preórdenes , o entre espacios topológicos finitos y preórdenes.
El nombre de "teorema de representación de Birkhoff" también se ha aplicado a otros dos resultados de Birkhoff, uno de 1935 sobre la representación de las álgebras de Boole como familias de conjuntos cerrados bajo unión, intersección y complemento (los llamados cuerpos de conjuntos , estrechamente relacionados con los anillos de conjuntos utilizados por Birkhoff para representar redes distributivas), y el teorema HSP de Birkhoff que representa las álgebras como productos de álgebras irreducibles. El teorema de representación de Birkhoff también se ha llamado el teorema fundamental para redes distributivas finitas . [2]
Muchos retículos pueden definirse de tal manera que los elementos del retículo se representen por conjuntos, la operación de unión del retículo se represente por la unión de conjuntos y la operación de encuentro del retículo se represente por la intersección de conjuntos. Por ejemplo, el retículo booleano definido a partir de la familia de todos los subconjuntos de un conjunto finito tiene esta propiedad. De manera más general, cualquier espacio topológico finito tiene un retículo de conjuntos como su familia de conjuntos abiertos. Debido a que las uniones e intersecciones de conjuntos obedecen a la ley distributiva , cualquier retículo definido de esta manera es un retículo distributivo. El teorema de Birkhoff establece que, de hecho, todos los retículos distributivos finitos pueden obtenerse de esta manera, y las generalizaciones posteriores del teorema de Birkhoff establecen algo similar para los retículos distributivos infinitos.
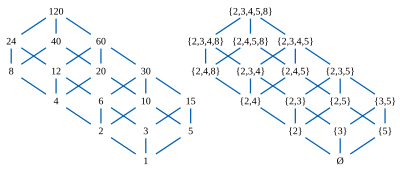
Consideremos los divisores de algún número compuesto, como (en la figura) 120, parcialmente ordenados por divisibilidad. Cualesquiera dos divisores de 120, como 12 y 20, tienen un único máximo común divisor 12 ∧ 20 = 4, el número más grande que los divide a ambos, y un único mínimo común múltiplo 12 ∨ 20 = 60; ambos números también son divisores de 120. Estas dos operaciones ∨ y ∧ satisfacen la ley distributiva, en cualquiera de dos formas equivalentes: ( x ∧ y ) ∨ z = ( x ∨ z ) ∧ ( y ∨ z ) y ( x ∨ y ) ∧ z = ( x ∧ z ) ∨ ( y ∧ z ), para todo x , y , y z . Por lo tanto, los divisores forman una red distributiva finita .
Se puede asociar cada divisor con el conjunto de potencias primos que lo dividen: así, 12 se asocia con el conjunto {2,3,4}, mientras que 20 se asocia con el conjunto {2,4,5}. Entonces, 12 ∧ 20 = 4 se asocia con el conjunto {2,3,4} ∩ {2,4,5} = {2,4}, mientras que 12 ∨ 20 = 60 se asocia con el conjunto {2,3,4} ∪ {2,4,5} = {2,3,4,5}, por lo que las operaciones de unión y encuentro del retículo corresponden a la unión e intersección de conjuntos.
Las potencias primas 2, 3, 4, 5 y 8 que aparecen como elementos en estos conjuntos pueden estar parcialmente ordenadas por divisibilidad; en este orden parcial más pequeño, 2 ≤ 4 ≤ 8 y no hay relaciones de orden entre otros pares. Los 16 conjuntos que están asociados con divisores de 120 son los conjuntos inferiores de este orden parcial más pequeño, subconjuntos de elementos tales que si x ≤ y e y pertenece al subconjunto, entonces x también debe pertenecer al subconjunto. De cualquier conjunto inferior L , se puede recuperar el divisor asociado calculando el mínimo común múltiplo de las potencias primas en L . Por lo tanto, el orden parcial de las cinco potencias primas 2, 3, 4, 5 y 8 lleva suficiente información para recuperar toda la red de divisibilidad original de 16 elementos.
El teorema de Birkhoff establece que esta relación entre las operaciones ∧ y ∨ de la red de divisores y las operaciones ∩ y ∪ de los conjuntos asociados de potencias primos no es casual y no depende de las propiedades específicas de los números primos y la divisibilidad: los elementos de cualquier red distributiva finita pueden asociarse con conjuntos inferiores de un orden parcial de la misma manera.
Como otro ejemplo, considere la red de subconjuntos de un conjunto de n elementos, parcialmente ordenados por inclusión. El teorema de Birkhoff muestra que esta red se produce por los conjuntos inferiores de la red distributiva libre en n generadores, cuyo número de elementos está dado por los números de Dedekind .
En un retículo, un elemento x es irreducible por unión si x no es la unión de un conjunto finito de otros elementos. De manera equivalente, x es irreducible por unión si no es ni el elemento inferior del retículo (la unión de cero elementos) ni la unión de dos elementos más pequeños. Por ejemplo, en el retículo de divisores de 120, no hay ningún par de elementos cuya unión sea 4, por lo que 4 es irreducible por unión. Un elemento x es primo por unión si difiere del elemento inferior, y siempre que x ≤ y ∨ z , o bien x ≤ y o bien x ≤ z . En el mismo retículo, 4 es primo por unión: siempre que mcm( y , z ) sea divisible por 4, al menos uno de y y z debe ser divisible por 4.
En cualquier red, un elemento que no es irreducible en el orden de las uniones no es primo en el orden de las uniones. De manera equivalente, un elemento que no es irreducible en el orden de las uniones no es primo en el orden de las uniones. Porque, si un elemento x no es irreducible en el orden de las uniones, existen y y z más pequeños tales que x = y ∨ z . Pero entonces x ≤ y ∨ z , y x no es menor o igual que y o z , lo que demuestra que no es primo en el orden de las uniones.
Existen retículos en los que los elementos primos de unión forman un subconjunto propio de los elementos irreducibles de unión, pero en un retículo distributivo los dos tipos de elementos coinciden. Supongamos que x es irreducible de unión y que x ≤ y ∨ z . Esta desigualdad es equivalente a la afirmación de que x = x ∧ ( y ∨ z ), y por la ley distributiva x = ( x ∧ y ) ∨ ( x ∧ z ). Pero como x es irreducible de unión, al menos uno de los dos términos en esta unión debe ser x mismo, mostrando que o bien x = x ∧ y (equivalentemente x ≤ y ) o bien x = x ∧ z (equivalentemente x ≤ z ).
El ordenamiento reticular del subconjunto de elementos irreducibles mediante unión forma un orden parcial ; el teorema de Birkhoff establece que el propio reticulado puede recuperarse a partir de los conjuntos inferiores de este orden parcial.

En cualquier orden parcial, los conjuntos inferiores forman una red en la que el ordenamiento parcial de la red está dado por la inclusión de conjuntos, la operación de unión corresponde a la unión de conjuntos y la operación de encuentro corresponde a la intersección de conjuntos, porque las uniones e intersecciones conservan la propiedad de ser un conjunto inferior. Como las uniones e intersecciones de conjuntos obedecen a la ley distributiva, se trata de una red distributiva. El teorema de Birkhoff establece que cualquier red distributiva finita se puede construir de esta manera.
Es decir, existe una correspondencia que preserva el orden uno a uno entre los elementos de L y los conjuntos inferiores del orden parcial. El conjunto inferior correspondiente a un elemento x de L es simplemente el conjunto de elementos irreducibles por unión de L que son menores o iguales a x , y el elemento de L correspondiente a un conjunto inferior S de elementos irreducibles por unión es la unión de S .
Para cualquier conjunto inferior S de elementos irreducibles por unión, sea x la unión de S , y sea T el conjunto inferior de los elementos irreducibles por unión menores o iguales a x . Entonces S = T . Porque, cada elemento de S pertenece claramente a T , y cualquier elemento irreducible por unión menor o igual a x debe (por primalidad de unión) ser menor o igual a uno de los miembros de S , y por lo tanto debe (por la suposición de que S es un conjunto inferior) pertenecer a S mismo. A la inversa, para cualquier elemento x de L , sea S los elementos irreducibles por unión menores o iguales a x , y sea y la unión de S . Entonces x = y . Porque, como una unión de elementos menores o iguales a x , y no puede ser mayor que x mismo, pero si x es irreducible por unión entonces x pertenece a S mientras que si x es la unión de dos o más elementos irreducibles por unión entonces deben pertenecer nuevamente a S , por lo que y ≥ x . Por tanto, la correspondencia es biunívoca y el teorema queda demostrado.
Birkhoff (1937) definió un anillo de conjuntos como una familia de conjuntos que está cerrada bajo las operaciones de uniones e intersecciones de conjuntos; más tarde, motivados por aplicaciones en psicología matemática , Doignon y Falmagne (1999) llamaron a la misma estructura un espacio de conocimiento cuasi-ordinal . Si los conjuntos en un anillo de conjuntos están ordenados por inclusión, forman una red distributiva. A los elementos de los conjuntos se les puede dar un preorden en el que x ≤ y siempre que algún conjunto en el anillo contenga x pero no y . El anillo de conjuntos en sí mismo es entonces la familia de conjuntos inferiores de este preorden, y cualquier preorden da lugar a un anillo de conjuntos de esta manera.
El teorema de Birkhoff, como se ha indicado anteriormente, es una correspondencia entre órdenes parciales individuales y redes distributivas. Sin embargo, también se puede extender a una correspondencia entre funciones de conservación del orden de órdenes parciales y homomorfismos acotados de las redes distributivas correspondientes. La dirección de estas funciones se invierte en esta correspondencia.
Sea 2 el orden parcial en el conjunto de dos elementos {0, 1}, con la relación de orden 0 < 1, y (siguiendo a Stanley) sea J(P) la red distributiva de conjuntos inferiores de un orden parcial finito P . Entonces los elementos de J(P) corresponden uno a uno a las funciones que preservan el orden de P a 2 . [2] Porque, si ƒ es una función de este tipo, ƒ −1 (0) forma un conjunto inferior, y a la inversa, si L es un conjunto inferior, se puede definir una función que preserva el orden ƒ L que mapea L a 0 y que mapea los elementos restantes de P a 1. Si g es cualquier función que preserva el orden de Q a P , se puede definir una función g * de J(P) a J(Q) que usa la composición de funciones para mapear cualquier elemento L de J(P) a ƒ L ∘ g . Esta función compuesta asigna Q a 2 y, por lo tanto, corresponde a un elemento g *( L ) = (ƒ L ∘ g ) −1 (0) de J(Q) . Además, para cualquier x e y en J(P) , g *( x ∧ y ) = g *( x ) ∧ g *( y ) (un elemento de Q se asigna por g al conjunto inferior x ∩ y si y solo si pertenece tanto al conjunto de elementos asignados a x como al conjunto de elementos asignados a y ) y simétricamente g *( x ∨ y ) = g *( x ) ∨ g *( y ). Además, el elemento inferior de J(P) (la función que asigna todos los elementos de P a 0) se asigna por g * al elemento inferior de J(Q) , y el elemento superior de J(P) se asigna por g * al elemento superior de J(Q) . Es decir, g * es un homomorfismo de redes acotadas.
Sin embargo, los elementos de P mismos se corresponden uno a uno con homomorfismos reticulares acotados de J(P) a 2 . Porque, si x es cualquier elemento de P , se puede definir un homomorfismo reticular acotado j x que mapea todos los conjuntos inferiores que contienen x a 1 y todos los otros conjuntos inferiores a 0. Y, para cualquier homomorfismo reticular de J(P) a 2 , los elementos de J(P) que se mapean a 1 deben tener un elemento mínimo único x (el encuentro de todos los elementos mapeados a 1), que debe ser irreducible por unión (no puede ser la unión de ningún conjunto de elementos mapeados a 0), por lo que cada homomorfismo reticular tiene la forma j x para algún x . Nuevamente, a partir de cualquier homomorfismo reticular acotado h de J(P) a J(Q) se puede usar la composición de funciones para definir un mapa que preserve el orden h * de Q a P . Se puede verificar que g ** = g para cualquier función que preserve el orden g de Q a P y que h ** = h para cualquier homomorfismo reticular acotado h de J(P) a J(Q) .
En terminología de teoría de categorías , J es un hom-functor contravariante J = Hom(—, 2 ) que define una dualidad de categorías entre, por un lado, la categoría de órdenes parciales finitos y mapas que preservan el orden, y por otro lado, la categoría de redes distributivas finitas y homomorfismos de redes acotadas.
En una red distributiva infinita, puede que no se dé el caso de que los conjuntos inferiores de los elementos irreducibles por unión estén en correspondencia biunívoca con los elementos de la red. De hecho, puede que no haya ningún irreducible por unión. Esto sucede, por ejemplo, en la red de todos los números naturales, ordenados con el orden inverso del orden de divisibilidad habitual (por lo que x ≤ y cuando y divide a x ): cualquier número x puede expresarse como la unión de los números xp y xq donde p y q son números primos distintos . Sin embargo, los elementos en redes distributivas infinitas todavía pueden representarse como conjuntos a través del teorema de representación de Stone para redes distributivas, una forma de dualidad de Stone en la que cada elemento de la red corresponde a un conjunto abierto compacto en un cierto espacio topológico . Este teorema de representación generalizado puede expresarse como una dualidad de teoría de categorías entre redes distributivas y espacios espectrales (a veces llamados espacios coherentes, pero no lo mismo que los espacios coherentes en lógica lineal ), espacios topológicos en los que los conjuntos abiertos compactos están cerrados bajo intersección y forman una base para la topología. [3] Hilary Priestley demostró que el teorema de representación de Stone podría interpretarse como una extensión de la idea de representar elementos de la red mediante conjuntos inferiores de un orden parcial, utilizando la idea de Nachbin de espacios topológicos ordenados. Los espacios de Stone con un orden parcial adicional vinculado con la topología a través del axioma de separación de Priestley también se pueden utilizar para representar redes distributivas acotadas. Dichos espacios se conocen como espacios de Priestley . Además, ciertos espacios bitopológicos , a saber, los espacios de Stone por pares , generalizan el enfoque original de Stone al utilizar dos topologías en un conjunto para representar una red distributiva abstracta. De este modo, el teorema de representación de Birkhoff se extiende al caso de redes distributivas infinitas (acotadas) de al menos tres maneras diferentes, resumidas en la teoría de dualidad para redes distributivas .
El teorema de representación de Birkhoff también puede generalizarse a estructuras finitas distintas de las redes distributivas. En una red distributiva, la operación de mediana autodual [4]
da lugar a un álgebra mediana , y la relación de recubrimiento de la red forma un grafo mediano . Las álgebras medianas finitas y los grafos medianos tienen una estructura dual como el conjunto de soluciones de una instancia de 2-satisfacibilidad ; Barthélemy y Constantin (1993) formulan esta estructura de manera equivalente como la familia de conjuntos estables iniciales en un grafo mixto . [5] Para una red distributiva, el grafo mixto correspondiente no tiene aristas no dirigidas, y los conjuntos estables iniciales son solo los conjuntos inferiores del cierre transitivo del grafo. De manera equivalente, para una red distributiva, el grafo de implicación de la instancia de 2-satisfacibilidad se puede dividir en dos componentes conectados , uno en las variables positivas de la instancia y el otro en las variables negativas; el cierre transitivo del componente positivo es el orden parcial subyacente de la red distributiva.
Otro resultado análogo al teorema de representación de Birkhoff, pero que se aplica a una clase más amplia de redes, es el teorema de Edelman (1980) que sostiene que cualquier red distributiva de unión finita puede representarse como un antimatroide , una familia de conjuntos cerrados bajo uniones pero en la que el cierre bajo intersecciones ha sido reemplazado por la propiedad de que cada conjunto no vacío tiene un elemento removible.