
El problema de Monty Hall es un acertijo , en forma de rompecabezas de probabilidad , basado nominalmente en el programa de televisión estadounidense Let's Make a Deal y llamado así por su presentador original, Monty Hall . El problema fue planteado originalmente (y resuelto) en una carta de Steve Selvin al American Statistician en 1975. [1] [2] Se hizo famoso como una pregunta de la carta del lector Craig F. Whitaker citada en la columna "Ask Marilyn" de Marilyn vos Savant en la revista Parade en 1990: [3]
Supongamos que estás en un concurso y te dan la opción de elegir entre tres puertas: detrás de una hay un coche; detrás de las otras, cabras. Eliges una puerta, digamos la número 1, y el presentador, que sabe qué hay detrás de las puertas, abre otra puerta, digamos la número 3, en la que hay una cabra. Luego te dice: "¿Quieres elegir la puerta número 2?" ¿Te conviene cambiar de opción?
La respuesta de Savant fue que el concursante debería cambiar a la otra puerta. [3] Según los supuestos estándar, la estrategia de cambio tiene un 2/3 probabilidad de ganar el coche, mientras que la estrategia de mantener la elección inicial solo tiene una 1/3 probabilidad.
Cuando el jugador hace su elección por primera vez, hay una2/3 probabilidad de que el coche esté detrás de una de las puertas no elegidas. Esta probabilidad no cambia después de que el anfitrión revele una cabra detrás de una de las puertas no elegidas. Cuando el anfitrión proporciona información sobre las dos puertas no elegidas (revelando que una de ellas no tiene el coche detrás), el 2/3La posibilidad de que el coche esté detrás de una de las puertas no elegidas depende de la puerta no elegida y no revelada, en contraposición a la1/3 probabilidad de que el coche esté detrás de la puerta elegida inicialmente por el concursante.
Las probabilidades dadas dependen de suposiciones específicas sobre cómo el anfitrión y el concursante eligen sus puertas. Una idea importante es que, con estas condiciones estándar, hay más información sobre las puertas 2 y 3 que la que estaba disponible al comienzo del juego cuando el jugador eligió la puerta 1: la acción del anfitrión agrega valor a la puerta no eliminada, pero no a la elegida originalmente por el concursante. Otra idea es que cambiar de puerta es una acción diferente a elegir entre las dos puertas restantes al azar, ya que la primera acción utiliza la información anterior y la segunda no. Otros posibles comportamientos del anfitrión distintos a los descritos pueden revelar información adicional diferente, o ninguna, y producir probabilidades diferentes.
Muchos lectores de la columna de Savant se negaron a creer que el cambio de método fuera beneficioso y rechazaron su explicación. Después de que el problema apareciera en Parade , aproximadamente 10.000 lectores, incluidos casi 1.000 con doctorados , escribieron a la revista, la mayoría de ellos calificando a Savant de equivocada. [4] Incluso cuando se les dieron explicaciones, simulaciones y pruebas matemáticas formales, muchas personas todavía no aceptaron que el cambio de método fuera la mejor estrategia. [5] Paul Erdős , uno de los matemáticos más prolíficos de la historia, no estaba convencido hasta que le mostraron una simulación por computadora que demostraba el resultado predicho por Savant. [6]
El problema es una paradoja del tipo verídico , porque la solución es tan contraintuitiva que puede parecer absurda pero, no obstante, es demostrablemente verdadera. El problema de Monty Hall está matemáticamente relacionado estrechamente con el problema de los tres prisioneros y con la mucho más antigua paradoja de la caja de Bertrand .
Steve Selvin escribió una carta al American Statistician en 1975, describiendo un problema basado en el programa de juegos Let's Make a Deal , [1] llamándolo el "problema de Monty Hall" en una carta posterior. [2] El problema es matemáticamente equivalente al problema de los Tres Prisioneros descrito en la columna "Juegos matemáticos" de Martin Gardner en Scientific American en 1959 [7] y al Problema de las Tres Conchas descrito en el libro de Gardner Aha Gotcha . [8]
Según los supuestos estándar, la probabilidad de ganar el auto después del cambio es2/3 . Esta solución se debe al comportamiento del anfitrión. Las ambigüedades en la versión Parade no definen explícitamente el protocolo del anfitrión. Sin embargo, la solución de Marilyn vos Savant [3] impresa junto con la pregunta de Whitaker implica, y tanto Selvin [1] como Savant [5] definen explícitamente, el rol del anfitrión de la siguiente manera:
Cuando se modifica cualquiera de estos supuestos, puede cambiar la probabilidad de ganar al cambiar de puerta, como se detalla en la sección siguiente. También se suele suponer que el coche está inicialmente escondido al azar detrás de las puertas y que, si el jugador elige inicialmente el coche, la elección del anfitrión de qué puerta para esconder cabras abrir es aleatoria. [10] Algunos autores, de forma independiente o inclusiva, suponen que la elección inicial del jugador también es aleatoria. [1]
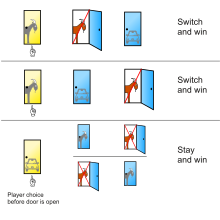
La solución presentada por Savant en Parade muestra las tres posibles disposiciones de un automóvil y dos cabras detrás de tres puertas y el resultado de permanecer o cambiar después de elegir inicialmente la puerta 1 en cada caso: [11]
Un jugador que se queda con la elección inicial gana sólo en una de tres de estas posibilidades igualmente probables, mientras que un jugador que cambia gana en dos de tres.
Una explicación intuitiva es que, si el concursante elige inicialmente una cabra (2 de 3 puertas), ganará el auto al cambiar porque ya no se puede elegir la otra cabra (el anfitrión tuvo que revelar su ubicación), mientras que si el concursante elige inicialmente el auto (1 de 3 puertas), no ganará el auto al cambiar. [12] Usando la estrategia de cambio, ganar o perder solo depende de si el concursante ha elegido inicialmente una cabra (2/3 probabilidad) o el coche ( 1/3 probabilidad). El hecho de que el anfitrión revele posteriormente una cabra en una de las puertas no elegidas no cambia nada en la probabilidad inicial. [13]

La mayoría de la gente concluye que el cambio no importa, porque habría un 50% de posibilidades de encontrar el coche detrás de cualquiera de las dos puertas sin abrir. Esto sería cierto si el anfitrión seleccionara una puerta para abrir al azar, pero este no es el caso. La puerta abierta por el anfitrión depende de la elección inicial del jugador, por lo que el supuesto de independencia no se cumple. Antes de que el anfitrión abra una puerta, hay un 1/3 probabilidad de que el coche esté detrás de cada puerta. Si el coche está detrás de la puerta 1, el anfitrión puede abrir la puerta 2 o la puerta 3, por lo que la probabilidad de que el coche esté detrás de la puerta 1 y el anfitrión abra la puerta 3 es 1/3×1/2 = 1/6 . Si el automóvil está detrás de la puerta 2 (y el jugador ha elegido la puerta 1), el anfitrión debe abrir la puerta 3, por lo que la probabilidad de que el automóvil esté detrás de la puerta 2 y el anfitrión abra la puerta 3 es 1/3× 1 = 1/3 . Estos son los únicos casos en los que el anfitrión abre la puerta 3, por lo que si el jugador ha elegido la puerta 1 y el anfitrión abre la puerta 3, el automóvil tiene el doble de probabilidades de estar detrás de la puerta 2 que de la puerta 1. La clave es que si el automóvil está detrás de la puerta 2, el anfitrión debe abrir la puerta 3, pero si el automóvil está detrás de la puerta 1, el anfitrión puede abrir cualquiera de las puertas.
Otra forma de entender la solución es considerar juntas las dos puertas inicialmente no elegidas por el jugador. [14] [15] [16] [17] [18] Como dice Cecil Adams , [14] "Monty está diciendo en efecto : puedes quedarte con una puerta o puedes tener las otras dos puertas".2/3La posibilidad de encontrar el coche no ha cambiado con la apertura de una de estas puertas porque Monty, al saber la ubicación del coche, seguramente revelará una cabra. La elección del jugador después de que el anfitrión abre una puerta no es diferente a si el anfitrión le ofreciera al jugador la opción de cambiar de la puerta elegida originalmente al conjunto de las dos puertas restantes. El cambio en este caso claramente le da al jugador una2/3 probabilidad de elegir el coche.
Como dice Keith Devlin , [15] "Al abrir su puerta, Monty le está diciendo al concursante 'Hay dos puertas que no elegiste, y la probabilidad de que el premio esté detrás de una de ellas es 2/3 . Te ayudaré usando mi conocimiento de dónde está el premio para abrir una de esas dos puertas y demostrarte que no esconde el premio. Ahora puedes aprovechar esta información adicional. Tu elección de la puerta A tiene una probabilidad de 1 en 3 de ser la ganadora. No he cambiado eso. Pero al eliminar la puerta C, te he demostrado que la probabilidad de que la puerta B esconda el premio es de 2 en 3. ' "
Savant sugiere que la solución será más intuitiva con 1.000.000 de puertas en lugar de 3. [3] En este caso, hay 999.999 puertas con cabras detrás de ellas y una puerta con un premio. Después de que el jugador elige una puerta, el anfitrión abre 999.998 de las puertas restantes. En promedio, en 999.999 veces de 1.000.000, la puerta restante contendrá el premio. Intuitivamente, el jugador debería preguntarse qué probabilidad hay de que, dado un millón de puertas, haya logrado elegir la correcta inicialmente. Stibel et al. propusieron que la demanda de memoria de trabajo se ve afectada durante el problema de Monty Hall y que esto obliga a las personas a "colapsar" sus elecciones en dos opciones igualmente probables. Informan que cuando el número de opciones aumenta a más de 7, las personas tienden a cambiar más a menudo; sin embargo, la mayoría de los concursantes todavía juzgan incorrectamente la probabilidad de éxito como del 50%. [18]
¡La has cagado, y la has cagado a lo grande! Como parece que tienes dificultades para comprender el principio básico que está en juego aquí, te lo explicaré. Después de que el anfitrión revele una cabra, ahora tienes una probabilidad de una entre dos de acertar. Tanto si cambias tu selección como si no, las probabilidades son las mismas. Hay suficiente analfabetismo matemático en este país y no necesitamos que el coeficiente intelectual más alto del mundo se propague más. ¡Qué vergüenza!
Scott Smith, Universidad de Florida [3]
Savant escribió en su primera columna sobre el problema de Monty Hall que el jugador debería cambiar de jugador. [3] Recibió miles de cartas de sus lectores, la gran mayoría de las cuales, incluidas muchas de lectores con doctorados, no estaban de acuerdo con su respuesta. Durante 1990-1991, tres de sus columnas más en Parade estuvieron dedicadas a la paradoja. [19] Numerosos ejemplos de cartas de lectores de las columnas de Savant se presentan y analizan en The Monty Hall Dilemma: A Cognitive Illusion Par Excellence . [20]
La discusión fue reproducida en otros medios (por ejemplo, en la columna de periódico " The Straight Dope " de Cecil Adams [14] ) y reportada en importantes periódicos como The New York Times . [4]
En un intento de aclarar su respuesta, propuso un juego de conchas [8] para ilustrarlo: "Miras hacia otro lado y yo pongo un guisante debajo de una de las tres conchas. Luego te pido que pongas tu dedo sobre una concha. Las probabilidades de que tu elección contenga un guisante son 1/3 ¿De acuerdo? Entonces simplemente levanto una concha vacía de las otras dos restantes. Como puedo (y lo haré) hacer esto independientemente de lo que hayas elegido, no hemos aprendido nada que nos permita revisar las probabilidades de la concha debajo de tu dedo". También propuso una simulación similar con tres cartas de juego.
Savant comentó que, si bien se produjo cierta confusión porque algunos lectores no se dieron cuenta de que se suponía que debían asumir que el anfitrión siempre debe revelar una cabra, casi todos sus numerosos corresponsales habían entendido correctamente las suposiciones del problema y, aun así, inicialmente estaban convencidos de que la respuesta de Savant ("cambio") era incorrecta.
Cuando se les presenta por primera vez el problema de Monty Hall, una abrumadora mayoría de personas asume que cada puerta tiene una probabilidad igual y concluye que cambiar no importa. [9] De 228 sujetos en un estudio, solo el 13% eligió cambiar. [21] En su libro El poder del pensamiento lógico , [22] el psicólogo cognitivo Massimo Piattelli Palmarini escribe: "Ningún otro rompecabezas estadístico se acerca tanto a engañar a todas las personas todo el tiempo [e] incluso los físicos Nobel dan sistemáticamente la respuesta incorrecta, e insisten en ello, y están listos para reprender por escrito a quienes proponen la respuesta correcta". Las palomas expuestas repetidamente al problema muestran que aprenden rápidamente a cambiar siempre, a diferencia de los humanos. [23]
La mayoría de las afirmaciones del problema, en particular la de Parade , no coinciden con las reglas del programa de juegos real [10] y no especifican completamente el comportamiento del anfitrión o que la ubicación del automóvil se selecciona al azar. [21] [4] [24] Sin embargo, Krauss y Wang argumentan que las personas hacen suposiciones estándar incluso si no se establecen explícitamente. [25]
Aunque estas cuestiones son matemáticamente significativas, incluso cuando se controlan estos factores, casi todas las personas siguen pensando que cada una de las dos puertas sin abrir tiene la misma probabilidad y concluyen que el cambio no importa. [9] Esta suposición de "igual probabilidad" es una intuición profundamente arraigada. [26] Las personas tienden fuertemente a pensar que la probabilidad se distribuye uniformemente entre tantas incógnitas como estén presentes, ya sea que lo esté o no. [27]
El problema sigue atrayendo la atención de los psicólogos cognitivos. El comportamiento típico de la mayoría, es decir, no cambiar, puede explicarse por fenómenos conocidos en la literatura psicológica como:
La evidencia experimental confirma que estas son explicaciones plausibles que no dependen de la intuición de la probabilidad. [31] [32] Otra posibilidad es que la intuición de la gente simplemente no se ocupe de la versión de libro de texto del problema, sino de un escenario de concurso real. [33] En ese caso, existe la posibilidad de que el maestro de ceremonias juegue con engaños abriendo otras puertas solo si inicialmente se eligió una puerta con el auto. Un maestro de ceremonias que juega con engaños la mitad de las veces modifica las posibilidades de ganar en caso de que a uno se le ofrezca cambiar a "igual probabilidad".
Como ya se ha comentado, la mayoría de las fuentes en el tema de probabilidad , incluidos muchos libros de texto introductorios de probabilidad, resuelven el problema mostrando las probabilidades condicionales de que el automóvil esté detrás de la puerta 1 y la puerta 2 .1/3 y 2/3 (no 1/2 y 1/2) dado que el concursante inicialmente elige la puerta 1 y el anfitrión abre la puerta 3; en las subsecciones anteriores se dieron varias formas de derivar y comprender este resultado.
Entre estas fuentes hay varias que critican explícitamente las soluciones "simples" presentadas popularmente, diciendo que estas soluciones son "correctas pero... inestables", [34] o no "abordan el problema planteado", [35] o son "incompletas", [36] o son "poco convincentes y engañosas", [37] o son (más claramente) "falsas". [38]
Sasha Volokh (2015) escribió que "cualquier explicación que diga algo como 'la probabilidad de la puerta 1 era 1/3 , y nada puede cambiar eso ...' es automáticamente sospechoso: las probabilidades son expresiones de nuestra ignorancia sobre el mundo, y nueva información puede cambiar el alcance de nuestra ignorancia". [39]
Algunos dicen que estas soluciones responden a una pregunta ligeramente diferente: una de ellas es "tienes que anunciar antes de que se abra una puerta si planeas cambiarte". [40]
Las soluciones simples muestran de diversas maneras que un concursante que está decidido a cambiar ganará el auto con probabilidad .2/3 , y por lo tanto, que cambiar es la estrategia ganadora, si el jugador tiene que elegir de antemano entre "cambiar siempre" y "quedarse siempre". Sin embargo, la probabilidad de ganar cambiando siempre es un concepto lógicamente distinto de la probabilidad de ganar cambiando dado que el jugador ha elegido la puerta 1 y el anfitrión ha abierto la puerta 3. Como dice una fuente, "la distinción entre [estas preguntas] parece confundir a muchos". [38] El hecho de que sean diferentes se puede demostrar variando el problema de modo que estas dos probabilidades tengan valores numéricos diferentes. Por ejemplo, supongamos que el concursante sabe que Monty no abre la segunda puerta al azar entre todas las alternativas legales, sino que, cuando se le da la oportunidad de elegir entre dos puertas perdedoras, Monty abrirá la de la derecha. En esta situación, las siguientes dos preguntas tienen respuestas diferentes:
La respuesta a la primera pregunta es 2/3 , como lo demuestran correctamente las soluciones "simples". Pero la respuesta a la segunda pregunta ahora es diferente: la probabilidad condicional de que el automóvil esté detrás de la puerta 1 o la puerta 2 dado que el anfitrión ha abierto la puerta 3 (la puerta de la derecha) es 1/2 . Esto se debe a que la preferencia de Monty por las puertas más a la derecha significa que abre la puerta 3 si el automóvil está detrás de la puerta 1 (que es lo que está originalmente con probabilidad 1/3) o si el coche está detrás de la puerta 2 (también originalmente con probabilidad )1/3 ). En esta variante, las dos preguntas arrojan respuestas diferentes. Esto se debe en parte a que la condición asumida de la segunda pregunta (que el anfitrión abra la puerta 3) solo se daría en esta variante con probabilidad 2/3 . Sin embargo, siempre que la probabilidad inicial de que el coche esté detrás de cada puerta sea 1/3 , nunca es una desventaja para el concursante cambiar, ya que la probabilidad condicional de ganar al cambiar es siempre al menos1/2 . [38]
En Morgan et al. , [38] cuatro profesores universitarios publicaron un artículo en The American Statistician en el que afirmaban que Savant había dado el consejo correcto pero el argumento equivocado. Creían que la pregunta era sobre la probabilidad de que el coche que estaba detrás de la puerta 2 estuviera dada la elección inicial del jugador de la puerta 1 y que el anfitrión del juego abriera la puerta 3, y demostraron que esta probabilidad era cualquier cosa entre 1/2 y 1 dependiendo del proceso de decisión del anfitrión dada la elección. Solo cuando la decisión es completamente aleatoria es la probabilidad 2/3 .
En un comentario invitado [41] y en cartas posteriores al editor, [42] [43] [44] [45] Morgan et al fueron apoyados por algunos escritores, criticados por otros; en cada caso, una respuesta de Morgan et al se publica junto con la carta o el comentario en The American Statistician . En particular, Savant se defendió vigorosamente. Morgan et al se quejaron en su respuesta a Savant [42] de que Savant todavía no había respondido realmente a su propio punto principal. Más tarde, en su respuesta a Hogbin y Nijdam, [45] estuvieron de acuerdo en que era natural suponer que el anfitrión elige una puerta para abrir completamente al azar cuando tiene una opción, y por lo tanto que la probabilidad condicional de ganar al cambiar (es decir, condicional dada la situación en la que se encuentra el jugador cuando tiene que hacer su elección) tiene el mismo valor ,2/3 , como la probabilidad incondicional de ganar al cambiar de posición (es decir, promediada sobre todas las situaciones posibles). Esta igualdad ya fue enfatizada por Bell (1992), quien sugirió que la solución matemáticamente compleja de Morgan et al. solo atraería a los estadísticos, mientras que la equivalencia de las soluciones condicional e incondicional en el caso de la simetría era intuitivamente obvia.
Hay desacuerdo en la literatura sobre si la formulación de Savant del problema, tal como se presenta en Parade , está haciendo la primera o la segunda pregunta, y si esta diferencia es significativa. [46] Behrends concluye que "Uno debe considerar el asunto con cuidado para ver que ambos análisis sean correctos", lo que no quiere decir que sean lo mismo. [47] Varios críticos del artículo de Morgan et al. , [38] cuyas contribuciones se publicaron junto con el artículo original, criticaron a los autores por alterar la redacción de Savant y malinterpretar su intención. [46] Un participante (William Bell) consideró que era una cuestión de gusto si uno menciona explícitamente que (según las condiciones estándar) qué puerta abre el anfitrión es independiente de si uno debería querer cambiar.
Entre las soluciones simples, la "solución de las puertas combinadas" es la que más se acerca a una solución condicional, como vimos en la discusión de los métodos que utilizan el concepto de probabilidades y el teorema de Bayes. Se basa en la intuición profundamente arraigada de que revelar información que ya se conoce no afecta a las probabilidades . Pero saber que el anfitrión puede abrir una de las dos puertas no elegidas para mostrar una cabra no significa que abrir una puerta específica no afecte la probabilidad de que el automóvil esté detrás de la puerta elegida inicialmente. El punto es que, aunque sabemos de antemano que el anfitrión abrirá una puerta y revelará una cabra, no sabemos qué puerta abrirá. Si el anfitrión elige uniformemente al azar entre las puertas que esconden una cabra (como es el caso en la interpretación estándar), esta probabilidad de hecho permanece inalterada, pero si el anfitrión puede elegir de manera no aleatoria entre tales puertas, entonces la puerta específica que abre el anfitrión revela información adicional. El anfitrión siempre puede abrir una puerta que revele una cabra y (en la interpretación estándar del problema) la probabilidad de que el coche esté detrás de la puerta elegida inicialmente no cambia, pero no es debido a lo primero que lo segundo es cierto. Las soluciones basadas en la afirmación de que las acciones del anfitrión no pueden afectar a la probabilidad de que el coche esté detrás de la puerta elegida inicialmente parecen persuasivas, pero la afirmación es simplemente falsa a menos que las dos opciones del anfitrión sean igualmente probables, si tiene una opción. [48] Por lo tanto, la afirmación necesita ser justificada; sin una justificación, la solución es, en el mejor de los casos, incompleta. Puede darse el caso de que la respuesta sea correcta pero el razonamiento utilizado para justificarla sea defectuoso.
Las soluciones simples anteriores muestran que un jugador con una estrategia de cambio gana el auto con una probabilidad general de 2/3 , es decir, sin tener en cuenta qué puerta abrió el anfitrión. [49] [13] De acuerdo con esto, la mayoría de las fuentes para el tema de probabilidad calculan las probabilidades condicionales de que el automóvil esté detrás de la puerta 1 y la puerta 2 como 1/3 y 2/3 respectivamente, dado que el concursante inicialmente elige la puerta 1 y el anfitrión abre la puerta 3. [2] [38] [50] [35] [13] [49] [36] Las soluciones en esta sección consideran solo aquellos casos en los que el jugador eligió la puerta 1 y el anfitrión abrió la puerta 3.
Si suponemos que el anfitrión abre una puerta al azar, cuando se le da la opción, entonces la puerta que abre el anfitrión no nos da ninguna información sobre si el automóvil está o no detrás de la puerta 1. En las soluciones simples, ya hemos observado que la probabilidad de que el automóvil esté detrás de la puerta 1, la puerta elegida inicialmente por el jugador, es inicialmente 1/3 . Además, el anfitrión seguramente va a abrir una puerta (diferente), por lo que abrir una puerta ( no se especifica qué puerta) no cambia esto .1/3 debe ser el promedio de: la probabilidad de que el auto esté detrás de la puerta 1, dado que el anfitrión eligió la puerta 2, y la probabilidad de que el auto esté detrás de la puerta 1, dado que el anfitrión eligió la puerta 3: esto se debe a que estas son las únicas dos posibilidades. Pero, estas dos probabilidades son las mismas. Por lo tanto, ambas son iguales a 1/3 . [38] Esto demuestra que la probabilidad de que el coche esté detrás de la puerta 1, dado que el jugador inicialmente eligió esta puerta y dado que el anfitrión abrió la puerta 3, es 1/3 , y se deduce que la probabilidad de que el automóvil esté detrás de la puerta 2, dado que el jugador inicialmente eligió la puerta 1 y el anfitrión abrió la puerta 3, es 2/3 . El análisis también muestra que la tasa de éxito general de 2/3 , logrado cambiando siempre , no se puede mejorar, y subraya lo que ya puede haber sido intuitivamente obvio: la elección que enfrenta el jugador es que entre la puerta elegida inicialmente y la otra puerta que el anfitrión dejó cerrada, los números específicos en estas puertas son irrelevantes.

Por definición, la probabilidad condicional de ganar por cambio de lugar dado que el concursante inicialmente elige la puerta 1 y el anfitrión abre la puerta 3 es la probabilidad del evento "el auto está detrás de la puerta 2 y el anfitrión abre la puerta 3" dividida por la probabilidad de "el anfitrión abre la puerta 3". Estas probabilidades se pueden determinar consultando la tabla de probabilidad condicional a continuación, o un árbol de decisión equivalente . [50] [13] [49] La probabilidad condicional de ganar por cambio de lugar es 1/3/1/3 + 1/6 , que es 2/3 . [2]
La siguiente tabla de probabilidad condicional muestra cómo se dividirían, en promedio, 300 casos, en todos los cuales el jugador elige inicialmente la puerta 1, según la ubicación del automóvil y la elección de puerta a abrir por parte del anfitrión.
Muchos libros de texto y artículos sobre probabilidad en el campo de la teoría de la probabilidad derivan la solución de probabilidad condicional a través de una aplicación formal del teorema de Bayes ; entre ellos, los libros de Gill [51] y Henze. [52] El uso de la forma de probabilidades del teorema de Bayes, a menudo llamada regla de Bayes, hace que dicha derivación sea más transparente. [34] [53]
Inicialmente, el coche tiene la misma probabilidad de estar detrás de cualquiera de las tres puertas: las probabilidades de que la puerta 1, la puerta 2 y la puerta 3 sean 1 : 1 : 1 . Esto sigue siendo así después de que el jugador haya elegido la puerta 1, por independencia. Según la regla de Bayes , las probabilidades posteriores de que el coche esté situado, dado que el anfitrión abre la puerta 3, son iguales a las probabilidades previas multiplicadas por el factor de Bayes o verosimilitud, que es, por definición, la probabilidad de que el nuevo dato (el anfitrión abre la puerta 3) bajo cada una de las hipótesis consideradas (ubicación del coche). Ahora bien, dado que el jugador eligió inicialmente la puerta 1, la probabilidad de que el anfitrión abra la puerta 3 es del 50% si el coche está detrás de la puerta 1, del 100% si el coche está detrás de la puerta 2, del 0% si el coche está detrás de la puerta 3. Por tanto, el factor de Bayes consta de las razones 1/2 : 1 : 0 o equivalentemente 1 : 2 : 0 , mientras que las probabilidades previas eran 1 : 1 : 1 . Por lo tanto, las probabilidades posteriores se vuelven iguales al factor de Bayes 1 : 2 : 0 . Dado que el anfitrión abrió la puerta 3, la probabilidad de que el automóvil esté detrás de la puerta 3 es cero, y es el doble de probable que esté detrás de la puerta 2 que de la puerta 1.
Richard Gill [54] analiza la probabilidad de que el anfitrión abra la puerta 3 de la siguiente manera. Dado que el coche no está detrás de la puerta 1, es igualmente probable que esté detrás de la puerta 2 o 3. Por lo tanto, la probabilidad de que el anfitrión abra la puerta 3 es del 50%. Dado que el coche está detrás de la puerta 1, la probabilidad de que el anfitrión abra la puerta 3 también es del 50%, porque, cuando el anfitrión tiene una elección, cualquiera de las dos opciones es igualmente probable. Por lo tanto, esté o no el coche detrás de la puerta 1, la probabilidad de que el anfitrión abra la puerta 3 es del 50%. La información "el anfitrión abre la puerta 3" contribuye con un factor de Bayes o razón de verosimilitud de 1 : 1 , sobre si el coche está o no detrás de la puerta 1. Inicialmente, las probabilidades de que la puerta 1 esconda el coche eran 2 : 1 . Por lo tanto, las probabilidades posteriores de que la puerta 1 esconda el coche siguen siendo las mismas que las probabilidades anteriores, 2 : 1 .
En palabras, la información sobre qué puerta abre el anfitrión (¿puerta 2 o puerta 3?) no revela información alguna sobre si el automóvil está o no detrás de la puerta 1, y esto es precisamente lo que los partidarios de las soluciones simples, o usando los modismos de las pruebas matemáticas, alegan que es intuitivamente obvio, "obviamente cierto, por simetría". [44]
Volviendo a Nalebuff, [55] el problema de Monty Hall también ha sido muy estudiado en la literatura sobre teoría de juegos y teoría de decisiones , y también algunas soluciones populares corresponden a este punto de vista. Savant pide una decisión, no una casualidad. Y los aspectos casuales de cómo se esconde el coche y cómo se abre una puerta no elegida son desconocidos. Desde este punto de vista, hay que recordar que el jugador tiene dos oportunidades de tomar decisiones: en primer lugar, qué puerta elegir inicialmente; y en segundo lugar, si cambiar o no. Puesto que no sabe cómo se esconde el coche ni cómo toma decisiones el anfitrión, puede hacer uso de su primera oportunidad de elección, por así decirlo, para neutralizar las acciones del equipo que dirige el concurso, incluido el anfitrión.
Siguiendo a Gill, [56] una estrategia de un concursante implica dos acciones: la elección inicial de una puerta y la decisión de cambiar (o quedarse) que puede depender tanto de la puerta elegida inicialmente como de la puerta a la que el anfitrión ofrece cambiar. Por ejemplo, la estrategia de un concursante es "elegir la puerta 1, luego cambiar a la puerta 2 cuando se le ofrece, y no cambiar a la puerta 3 cuando se le ofrece". Existen doce estrategias deterministas de este tipo del concursante.
La comparación elemental de las estrategias de los concursantes muestra que, por cada estrategia A, hay otra estrategia B "elige una puerta y luego cambia sin importar lo que pase" que la domina. [57] No importa cómo se esconda el auto y no importa qué regla use el anfitrión cuando tiene que elegir entre dos cabras, si A gana el auto, B también lo hace. Por ejemplo, la estrategia A "elige la puerta 1 y luego quédate siempre con ella" está dominada por la estrategia B "elige la puerta 2 y luego cambia siempre después de que el anfitrión revele una puerta": A gana cuando la puerta 1 oculta el auto, mientras que B gana cuando cualquiera de las puertas 1 o 3 oculta el auto. De manera similar, la estrategia A "elige la puerta 1 y luego cambia a la puerta 2 (si se ofrece), pero no cambia a la puerta 3 (si se ofrece)" está dominada por la estrategia B "elige la puerta 2 y luego cambia siempre". A gana cuando la puerta 1 oculta el auto y Monty elige abrir la puerta 2 o si la puerta 3 oculta el auto. La estrategia B gana cuando la puerta 1 o la puerta 3 ocultan el automóvil, es decir, siempre que A gane más el caso en el que la puerta 1 oculta el automóvil y Monty decide abrir la puerta 3.
La dominancia es una razón de peso para buscar una solución entre las estrategias que cambian constantemente, bajo supuestos bastante generales sobre el entorno en el que el concursante está tomando decisiones. En particular, si el auto se oculta mediante algún mecanismo de aleatorización (como lanzar un dado simétrico o asimétrico de tres caras), la dominancia implica que una estrategia que maximice la probabilidad de ganar el auto estará entre tres estrategias que cambian constantemente, es decir, será la estrategia que inicialmente elija la puerta menos probable y luego cambie sin importar qué puerta cambiar ofrezca el anfitrión.
El dominio estratégico vincula el problema de Monty Hall con la teoría de juegos . En el escenario de juego de suma cero de Gill, [56] descartar las estrategias que no implican cambio reduce el juego a la siguiente variante simple: el presentador (o el equipo de televisión) decide en qué puerta se esconde el coche, y el concursante elige dos puertas (es decir, las dos puertas que quedan después de la primera elección nominal del jugador). El concursante gana (y su oponente pierde) si el coche está detrás de una de las dos puertas que eligió.

Una forma sencilla de demostrar que una estrategia de cambio realmente gana dos de cada tres veces con las suposiciones estándar es simular el juego con cartas . [58] [59] Se utilizan tres cartas de una baraja normal para representar las tres puertas; una carta "especial" representa la puerta con el coche y otras dos cartas representan las puertas de las cabras.
La simulación se puede repetir varias veces para simular varias rondas del juego. El jugador elige una de las tres cartas y, luego, al mirar las dos cartas restantes, el "anfitrión" descarta una carta de cabra. Si la carta que queda en la mano del anfitrión es la carta de auto, esto se registra como una victoria por cambio; si el anfitrión tiene una carta de cabra, la ronda se registra como una victoria por permanencia. Como este experimento se repite en varias rondas, es probable que la tasa de victorias observada para cada estrategia se aproxime a su probabilidad de victoria teórica, de acuerdo con la ley de los grandes números .
Las repeticiones de jugadas también dejan más claro por qué el cambio es la mejor estrategia. Después de que el jugador elige su carta, ya está determinado si el cambio le permitirá ganar la ronda. Si esto no es convincente, la simulación se puede hacer con todo el mazo. [58] [14] En esta variante, la carta de auto va al anfitrión 51 veces de 52, y se queda con el anfitrión sin importar cuántas cartas que no sean de auto se descarten.
Una variante común del problema, asumida por varios autores académicos como el problema canónico , no hace la suposición simplificadora de que el anfitrión debe elegir uniformemente la puerta a abrir, sino que usa alguna otra estrategia . La confusión en cuanto a qué formalización es autoritativa ha llevado a una acritud considerable, particularmente porque esta variante hace que las demostraciones sean más complejas sin alterar la optimalidad de la estrategia de siempre cambiar para el jugador. En esta variante, el jugador puede tener diferentes probabilidades de ganar dependiendo de la elección observada del anfitrión, pero en cualquier caso la probabilidad de ganar cambiando es al menos 1/2 (y puede ser tan alta como 1), mientras que la probabilidad general de ganar al cambiar sigue siendo exactamente 2/3 . Las variantes se presentan a veces en sucesión en libros de texto y artículos destinados a enseñar los conceptos básicos de la teoría de la probabilidad y la teoría de juegos . También se han estudiado un número considerable de otras generalizaciones.
La versión del problema de Monty Hall publicada en Parade en 1990 no decía específicamente que el anfitrión siempre abriría otra puerta, o que siempre ofrecería la opción de cambiar, o incluso que nunca abriría la puerta que revelaba el auto. Sin embargo, Savant dejó en claro en su segunda columna de seguimiento que el comportamiento del anfitrión previsto solo podía ser lo que condujo al problema.2/3 probabilidad que dio como su respuesta original. "Cualquier otra cosa es una pregunta diferente". [5] "Prácticamente todos mis críticos entendieron el escenario previsto. Personalmente leí casi tres mil cartas (de los muchos miles adicionales que llegaron) y encontré que casi todas insistían simplemente en que debido a que quedaban dos opciones (o un error equivalente), las probabilidades eran iguales. Muy pocos plantearon preguntas sobre la ambigüedad, y las cartas realmente publicadas en la columna no estaban entre esas pocas". [60] La respuesta sigue si el auto se coloca al azar detrás de cualquier puerta, el anfitrión debe abrir una puerta que revele una cabra independientemente de la elección inicial del jugador y, si hay dos puertas disponibles, elige cuál abrir al azar. [9] La tabla a continuación muestra una variedad de otros posibles comportamientos del anfitrión y el impacto en el éxito del cambio.
Determinar la mejor estrategia del jugador dentro de un conjunto dado de otras reglas que el anfitrión debe seguir es el tipo de problema que se estudia en la teoría de juegos . Por ejemplo, si no se le exige al anfitrión que haga la oferta de cambiar el coche, el jugador puede sospechar que el anfitrión es malicioso y hacer las ofertas con más frecuencia si el jugador ha seleccionado inicialmente el coche. En general, la respuesta a este tipo de pregunta depende de las suposiciones específicas que se hagan sobre el comportamiento del anfitrión, y puede variar desde "ignorar al anfitrión por completo" hasta "lanzar una moneda y cambiar el coche si sale cara"; consulte la última fila de la tabla a continuación.
Morgan et al [38] y Gillman [35] muestran una solución más general en la que el coche se coloca de forma aleatoria (uniforme) pero el anfitrión no está obligado a elegir de forma aleatoria uniforme si el jugador ha seleccionado inicialmente el coche, que es como ambos interpretan el enunciado del problema en Parade a pesar de las advertencias del autor. Ambos cambiaron la redacción de la versión de Parade para enfatizar ese punto cuando reformularon el problema. Consideran un escenario en el que el anfitrión elige entre revelar dos cabras con una preferencia expresada como una probabilidad q , que tiene un valor entre 0 y 1. Si el anfitrión elige aleatoriamente, q sería 1/2 y cambiar gana con probabilidad 2/3 independientemente de qué puerta abra el anfitrión. Si el jugador elige la puerta 1 y la preferencia del anfitrión por la puerta 3 es q , entonces la probabilidad de que el anfitrión abra la puerta 3 y el auto esté detrás de la puerta 2 es 1/3 , mientras que la probabilidad de que el anfitrión abra la puerta 3 y el automóvil esté detrás de la puerta 1 es q/3 . Estos son los únicos casos en los que el anfitrión abre la puerta 3, por lo que la probabilidad condicional de ganar cambiando dado que el anfitrión abre la puerta 3 es 1/3/1/3 + q /3 lo cual se simplifica a 1/1 + q . Dado que q puede variar entre 0 y 1, esta probabilidad condicional puede variar entre 1/2 y 1. Esto significa que incluso sin obligar al anfitrión a elegir aleatoriamente si el jugador inicialmente selecciona el auto, el jugador nunca está en peores condiciones si cambia. Sin embargo, ninguna fuente sugiere que el jugador sepa cuál es el valor de q , por lo que el jugador no puede atribuir una probabilidad distinta a la 2/3 que Savant asumió que estaba implícito.
DL Ferguson (1975 en una carta a Selvin [2] ) sugiere una generalización de N puertas del problema original en la que el anfitrión abre p puertas perdedoras y luego ofrece al jugador la oportunidad de cambiar; en esta variante, cambiar gana con una probabilidad . Esta probabilidad siempre es mayor que , por lo tanto, cambiar siempre trae una ventaja.
Incluso si el anfitrión abre solo una puerta ( ), el jugador está mejor cambiando en todos los casos. A medida que N crece, la ventaja disminuye y se acerca a cero. [64] En el otro extremo, si el anfitrión abre todas las puertas perdedoras menos una ( p = N − 2) la ventaja aumenta a medida que N crece (la probabilidad de ganar cambiando es N -1/norte , que se acerca a 1 a medida que N se hace muy grande).
Una versión cuántica de la paradoja ilustra algunos puntos sobre la relación entre la información clásica o no cuántica y la información cuántica , tal como está codificada en los estados de los sistemas mecánicos cuánticos. La formulación se basa vagamente en la teoría de juegos cuánticos . Las tres puertas se reemplazan por un sistema cuántico que permite tres alternativas; abrir una puerta y mirar detrás de ella se traduce como hacer una medición particular. Las reglas se pueden establecer en este lenguaje, y una vez más la elección para el jugador es quedarse con la opción inicial o cambiar a otra opción "ortogonal". La última estrategia resulta duplicar las posibilidades, al igual que en el caso clásico. Sin embargo, si el presentador del programa no ha aleatorizado la posición del premio de una manera completamente mecánica cuántica, el jugador puede hacerlo incluso mejor, y a veces incluso puede ganar el premio con certeza. [65] [66]
El primero de varios acertijos de probabilidad relacionados con el problema de Monty Hall es la paradoja de la caja de Bertrand , planteada por Joseph Bertrand en 1889 en su Calcul des probabilités . [67] En este acertijo, hay tres cajas: una caja que contiene dos monedas de oro, una caja con dos monedas de plata y una caja con una de cada una. Después de elegir una caja al azar y retirar una moneda al azar que resulta ser una moneda de oro, la pregunta es cuál es la probabilidad de que la otra moneda sea de oro. Al igual que en el problema de Monty Hall, la respuesta intuitiva es 1/2 , pero la probabilidad es en realidad 2/3 .
El problema de los tres prisioneros , publicado en la columna Mathematical Games de Martin Gardner en Scientific American en 1959 [7] [58] es equivalente al problema de Monty Hall. Este problema involucra a tres prisioneros condenados, uno de los cuales ha sido elegido al azar en secreto para ser indultado. Uno de los prisioneros le ruega al alcaide que le diga el nombre de uno de los otros que serán ejecutados, argumentando que esto no revela información sobre su propio destino pero aumenta sus posibilidades de ser indultado .1/3 a 1/2 . El director obliga a lanzar una moneda (en secreto) para decidir qué nombre proporcionar si el prisionero que pregunta es el que va a ser indultado. La pregunta es si conocer la respuesta del director cambia las posibilidades del prisionero de ser indultado. Este problema es equivalente al problema de Monty Hall; el prisionero que hace la pregunta todavía tiene una 1/3 tiene posibilidades de ser indultado, pero su colega anónimo tiene una 2/3 oportunidad.
Steve Selvin planteó el problema de Monty Hall en un par de cartas a The American Statistician en 1975. [1] [2] La primera carta presentaba el problema en una versión similar a su presentación en Parade 15 años después. La segunda parece ser la primera vez que se utiliza el término "problema de Monty Hall". El problema es en realidad una extrapolación del concurso. Monty Hall abrió una puerta equivocada para generar entusiasmo, pero ofreció un premio menor conocido (como 100 dólares en efectivo) en lugar de la opción de cambiar de puerta. Como Monty Hall le escribió a Selvin:
Y si alguna vez entras en mi programa, las reglas se mantendrán vigentes para ti: no se permiten intercambios de cajas después de la selección.
—Monty Hall [68]
En 1987, en la sección Puzzles de The Journal of Economic Perspectives , se publicó una versión del problema muy similar a la que apareció tres años después en Parade . Nalebuff, como otros autores posteriores en economía matemática, ve el problema como un ejercicio simple y divertido de teoría de juegos . [55]
"La trampa de Monty Hall", artículo de Phillip Martin de 1989 en Bridge Today , presentó el problema de Selvin como un ejemplo de lo que Martin llama la trampa de probabilidad de tratar la información no aleatoria como si fuera aleatoria, y relaciona esto con conceptos del juego de bridge . [69]
Una versión reformulada del problema de Selvin apareció en la columna de preguntas y respuestas de Marilyn vos Savant , Ask Marilyn, de Parade en septiembre de 1990. [3] Aunque Savant dio la respuesta correcta de que cambiar de tema ganaría dos tercios de las veces, estima que la revista recibió 10.000 cartas, incluidas cerca de 1.000 firmadas por doctores, muchas de ellas con membretes de departamentos de matemáticas y ciencias, declarando que su solución era incorrecta. [4] Debido a la abrumadora respuesta, Parade publicó cuatro columnas sin precedentes sobre el problema. [70] Como resultado de la publicidad, el problema se ganó el nombre alternativo de "Marilyn y las cabras".
En noviembre de 1990, en la columna de Cecil Adams " The Straight Dope " se produjo un debate igualmente polémico sobre el artículo de Savant . [14] Adams respondió inicialmente, incorrectamente, que las probabilidades de que las dos puertas restantes salieran deben ser de una entre dos. Después de que un lector escribiera para corregir las matemáticas del análisis de Adams, Adams aceptó que matemáticamente se había equivocado. "Eliges la puerta número 1. Ahora te ofrecen esta opción: abrir la puerta número 1, o abrir la puerta número 2 y la puerta número 3. En este último caso, te quedas con el premio si está detrás de cualquiera de las puertas. Preferirías tener dos posibilidades entre tres de conseguir el premio que una entre tres, ¿no? Si lo piensas, el problema original te ofrece básicamente la misma opción. Monty está diciendo, en efecto: puedes quedarte con una puerta o puedes quedarte con las otras dos puertas, una de las cuales (una puerta sin premio) te la abriré yo". Adams dijo que la versión de Parade no establecía restricciones críticas y que, sin ellas, las probabilidades de ganar cambiando de lugar no eran necesariamente de dos en tres (por ejemplo, no era razonable suponer que el anfitrión siempre abre una puerta). Sin embargo, numerosos lectores escribieron para afirmar que Adams había tenido "razón la primera vez" y que las probabilidades correctas eran de una en dos.
La columna Parade y su respuesta recibieron una considerable atención en la prensa, incluyendo un artículo de primera plana en The New York Times en el que se entrevistó al propio Monty Hall . [4] Hall comprendió el problema, le dio al periodista una demostración con las llaves del coche y le explicó cómo el juego real en Let's Make a Deal difería de las reglas del rompecabezas. En el artículo, Hall señaló que como tenía control sobre la forma en que progresaba el juego, jugando con la psicología del concursante, la solución teórica no se aplicaba al juego real del programa. Dijo que no le sorprendió la insistencia de los expertos en que la probabilidad era de 1 de 2. "Esa es la misma suposición que harían los concursantes en el programa después de que les mostrara que no había nada detrás de una puerta", dijo. "Pensarían que las probabilidades de que su puerta estuviera ahora en 1 de 2, por lo que odiarían ceder la puerta sin importar cuánto dinero les ofreciera. Al abrir esa puerta estábamos aplicando presión. Lo llamamos el tratamiento Henry James . Era ' La vuelta de tuerca '". Hall aclaró que, como presentador de un programa de juegos, no tenía que seguir las reglas del rompecabezas de la columna Savant y no siempre tenía que permitir que una persona tuviera la oportunidad de cambiar (por ejemplo, podía abrirle la puerta inmediatamente si era una puerta perdedora, podía ofrecerle dinero para que no cambiara de una puerta perdedora a una puerta ganadora, o podía permitirle la oportunidad de cambiar sólo si tenía una puerta ganadora). "Si el presentador tiene que abrir una puerta todo el tiempo y ofrecerle un cambio, entonces debe aceptar el cambio", dijo. "Pero si tiene la opción de permitirle un cambio o no, tenga cuidado. Caveat emptor. Todo depende de su estado de ánimo".
La novela Mr. Mee (2000) de Andrew Crumey contiene una versión del problema de Monty Hall ambientada en el siglo XVIII. En el capítulo 1 se presenta como un juego de trileros que un prisionero debe ganar para salvar su vida. En el capítulo 8, el filósofo Rosier, su alumno Tissot y la esposa de Tissot prueban las probabilidades mediante simulación y verifican el resultado contra-intuitivo. Luego realizan un experimento con cuentas blancas y negras que se asemeja a la paradoja del niño o la niña , y en una alusión humorística a la paradoja de Einstein-Podolsky-Rosen , Rosier concluye erróneamente que "tan pronto como vi mi propia cuenta, una ola de probabilidad pura voló, instantáneamente, de un extremo de la habitación al otro. Esto explicó el cambio repentino de dos tercios a la mitad, ya que un cuanto finito de probabilidad (de peso un sexto) pasó milagrosamente entre las cuentas, lanzado por mi propio acto de observación". [71] Rosier explica su teoría a Tissot, pero "su pobre comprensión de mis teorías salió a la luz algunos días después cuando, como su hermana estaba a punto de dar a luz, Tissot pagó para que enviaran a una niña a la habitación, creyendo que eso haría que el nuevo niño tuviera el doble de probabilidades de nacer varón. Sin embargo, mi alumno ganó una sobrina; y no tuve ninguna dificultad en explicar la falacia de su razonamiento. Tissot simplemente había entendido mal mi notable Paradoja de los gemelos, que establece que si un niño te dice que tiene un hermano, entonces la probabilidad de que sea una hermana no es la mitad, sino dos tercios". [72] A esto le sigue una versión de la inesperada paradoja del ahorcado .
En el capítulo 101 de El curioso incidente del perro a medianoche (2003) de Mark Haddon , el narrador Christopher analiza el problema de Monty Hall, describe su historia y su solución. Concluye: "Esto demuestra que la intuición a veces puede hacer que las cosas se equivoquen. Y la intuición es lo que la gente usa en la vida para tomar decisiones. Pero la lógica puede ayudarte a encontrar la respuesta correcta". [73]
{{cite journal}}: Mantenimiento de CS1: postscript ( enlace ){{cite web}}: Mantenimiento de CS1: postscript ( enlace ){{cite journal}}: Mantenimiento CS1: fecha y año ( enlace )