Disfenoide desaire

Poliedro convexo con 12 caras triangulares.

En geometría , el disfenoide chato es un poliedro convexo con 12 triángulos equiláteros como caras . Es un ejemplo de deltaedro y sólido de Johnson . Se puede construir de diferentes maneras. Esta forma también tiene nombres alternativos llamados dodecaedro siamés , dodecaedro triangular , dodecaedro trigonal o dodecaedro ; estos nombres significan poliedro de 12 lados.

Las aplicaciones del disfenoide chato se pueden visualizar como un grupo de átomos que rodea un átomo central, es decir, la geometría molecular dodecaédrica . Sus vértices pueden ubicarse en una esfera y también pueden usarse como el potencial mínimo de Lennard-Jones posible entre todos los grupos de ocho esferas. El poliedro dual del disfenoide chato es el girobifastigium alargado .

Construcción

Involucrando poliedro

El disfenoide chato se puede construir de diferentes maneras. Como sugiere el nombre, el disfenoide chato se construye a partir de un disfenoide tetragonal cortando todos los bordes de sus caras y agregando triángulos equiláteros (los colores azul claro en la siguiente imagen) que están retorcidos en un cierto ángulo entre ellos. ^{[ cita necesaria ]} Este proceso de construcción se conoce como desaire . ^[1]

Proceso de construcción de disfenoide chato mediante desaire.

El diefenoides chato también se puede construir a partir de una bipirámide triangular, cortando sus dos bordes a lo largo de los ápices. Estos ápices se pueden empujar uno hacia el otro, lo que hace que los dos nuevos vértices se alejen. ^[2] Alternativamente, el diefenoides chato se puede construir a partir de una bipirámide pentagonal cortando los dos bordes a lo largo del que conecta la base de la bipirámide y luego insertando dos triángulos equiláteros entre ellos. ^[3] Otra forma de construir el diefenoides chato se parte del antiprisma cuadrado , reemplazando las dos caras cuadradas por pares de triángulos equiláteros. Otra construcción del diefenoides chato es la de una girobianticúpula digonal . Tiene la misma topología y simetría pero sin triángulos equiláteros. Tiene 4 vértices en un cuadrado en un plano central como dos anticúpulas unidas con simetría rotacional.

Se puede formar un modelo físico del disfenoide chato doblando una red formada por 12 triángulos equiláteros (un diamante de 12 ), como se muestra. Una red alternativa sugerida por John Montroll tiene menos vértices cóncavos en su límite, lo que la hace más conveniente para la construcción de origami . ^[4]

Por coordenadas cartesianas

A los ocho vértices del disfenoides chato se les pueden dar coordenadas cartesianas :

$${\displaystyle {\begin{aligned}(\pm t,r,0),&\qquad (0,-r,\pm t),\\(\pm 1,-s,0),&\qquad (0,s,\pm 1).\end{aligned}}}$$

del polinomio cúbico^[5] ${\displaystyle q\approx 0.16902}$ ${\textstyle 2x^{3}+11x^{2}+4x-1.}$ ${\displaystyle r}$ ${\displaystyle s}$ ${\displaystyle t}$

$${\displaystyle r={\sqrt {q}}\approx 0.41112,\qquad s={\sqrt {\frac {1-q}{2q}}}\approx 1.56786,\qquad t=2rs={\sqrt {2-2q}}\approx 1.28917.}$$

construir con compás y regla^[2]

Propiedades

Como consecuencia de tales construcciones, el diefenoides chato tiene 12 triángulos equiláteros. Un deltaedro es un poliedro en el que todas las caras son triángulos equiláteros. Hay ocho deltaedros convexos, uno de los cuales es el diefenoides chato. ^[6] De manera más general, el poliedro convexo en el que todas las caras son polígonos regulares son los sólidos de Johnson , y todo deltaedro convexo es el sólido de Johnson. El disfenoide chato se encuentra entre ellos, enumerado como el 84º sólido de Johnson . ^[7] ${\displaystyle J_{84}}$

Medición

Un diefenoides chato con borde largo tiene un área de superficie: ^[8] ${\displaystyle a}$

$${\displaystyle A=3{\sqrt {3}}a^{2}\approx 5.19615a^{2},}$$

^[8]

$${\displaystyle V\approx 0.85949a^{3}.}$$

Simetría y geodésica.

Modelo 3D de un diefenoides chato.

El disfenoide chato tiene las mismas simetrías que un disfenoide tetragonal , la simetría antiprismática de orden 8: tiene un eje de simetría rotacional de 180° a través de los puntos medios de sus dos bordes opuestos, dos planos perpendiculares de simetría de reflexión a través de este eje y cuatro adicionales. Operaciones de simetría dadas por una reflexión perpendicular al eje seguida de un cuarto de vuelta y posiblemente otra reflexión paralela al eje. ^[6] . ${\displaystyle D_{2\mathrm {d} }}$

Hasta las simetrías y la traslación paralela, el disfenoide chato tiene cinco tipos de geodésicas cerradas simples (que no se cruzan por sí solas) . Estos son caminos en la superficie del poliedro que evitan los vértices y localmente parecen el camino más corto: siguen segmentos de línea recta a través de cada cara del poliedro que cruzan, y cuando cruzan un borde del poliedro forman ángulos complementarios en los dos incidentes miran hacia el borde. Intuitivamente, se podría estirar una banda elástica alrededor del poliedro a lo largo de este camino y permanecería en su lugar: no hay manera de cambiar localmente el camino y hacerlo más corto. Por ejemplo, un tipo de geodésica cruza los dos bordes opuestos del diefenoides chato en sus puntos medios (donde el eje de simetría sale del politopo) en un ángulo de . Un segundo tipo de geodésica pasa cerca de la intersección del diefenoides chato con el plano que biseca perpendicularmente el eje de simetría (el ecuador del poliedro), cruzando los bordes de ocho triángulos en ángulos que se alternan entre y . Desplazar una geodésica en la superficie del poliedro en una cantidad pequeña (lo suficientemente pequeña como para que el desplazamiento no haga que cruce ningún vértice) preserva la propiedad de ser una geodésica y preserva su longitud, por lo que ambos ejemplos tienen versiones desplazadas de la del mismo tipo que están colocados de manera menos simétrica. Las longitudes de las cinco geodésicas cerradas simples sobre un diefenoides chato con aristas de longitud unitaria son ${\displaystyle \pi /3}$ ${\displaystyle \pi /2}$ ${\displaystyle \pi /6}$

${\displaystyle 2{\sqrt {3}}\approx 3.464}$(para la geodésica ecuatorial), , (para la geodésica a través de los puntos medios de bordes opuestos), y . ${\displaystyle {\sqrt {13}}\approx 3.606}$ ${\displaystyle 4}$ ${\displaystyle 2{\sqrt {7}}\approx 5.292}$ ${\displaystyle {\sqrt {19}}\approx 4.359}$

A excepción del tetraedro, que tiene infinitos tipos de geodésicas cerradas simples, el disfenoide chato tiene la mayor cantidad de tipos de geodésicas de cualquier deltaedro. ^[9]

Representación por el gráfico.

El diefenoides chato tiene 4 conexiones , lo que significa que es necesario eliminar cuatro vértices para desconectar los vértices restantes. Es uno de los cuatro poliedros bien cubiertos simpliciales de 4 conectados , lo que significa que todos los conjuntos independientes máximos de sus vértices tienen el mismo tamaño. Los otros tres poliedros con esta propiedad son el octaedro regular , la bipirámide pentagonal y un poliedro irregular de 12 vértices y 20 caras triangulares. ^[10]

Poliedro dual

El poliedro dual del girobifastigium alargado.

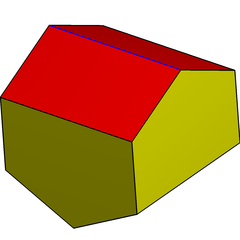
El poliedro dual del disfenoide chato es el girobifastigium alargado . Tiene pentágonos en ángulo recto y puede autoteselar el espacio.

Aplicaciones

Las esferas centradas en los vértices del diefenoides chato forman un grupo que, según experimentos numéricos, tiene el potencial de Lennard-Jones mínimo posible entre todos los grupos de ocho esferas. ^[5]

En la geometría de los compuestos químicos , un poliedro puede visualizarse como el grupo de átomos que rodea a un átomo central. La geometría molecular dodecaédrica describe el grupo para el cual es un disfenoide chato. ^[11]

Historia y denominación

Esta forma fue denominada dodecaedro siamés en el artículo de Hans Freudenthal y BL van der Waerden (1947), que describieron por primera vez el conjunto de ocho deltaedros convexos . ^[12]

El nombre de dodecadeltaedro fue dado a la misma forma por Bernal (1964), en referencia a que se trata de un deltaedro de 12 lados. Existen otros dodecaedros simpliciales , como la bipirámide hexagonal , pero ésta es la única que se puede realizar con caras equiláteras. Bernal estaba interesado en las formas de los agujeros dejados en disposiciones irregulares de esferas compactas, por lo que utilizó una definición restrictiva de deltaedro, en la que un deltaedro es un poliedro convexo con caras triangulares que pueden formarse mediante los centros de una colección de congruentes. esferas, cuyas tangencias representan bordes de poliedro, y de manera que no hay espacio para empaquetar otra esfera dentro de la jaula creada por este sistema de esferas. Esta definición restrictiva no permite la bipirámide triangular (porque forma dos agujeros tetraédricos en lugar de un solo agujero), la bipirámide pentagonal (porque las esferas de sus vértices se interpenetran, por lo que no puede ocurrir en empaquetamientos de esferas) y el icosaedro (porque tiene espacio interior para otro). esfera). Bernal escribe que el disfenoide chato es "una coordinación muy común para el ion calcio en cristalografía ". ^[13] En geometría de coordinación, generalmente se le conoce como dodecaedro trigonal o simplemente como dodecaedro. ^{[2] [ cita necesaria ]}

El nombre disfenoide chato proviene de la clasificación de Norman Johnson de 1966 de los sólidos de Johnson , poliedros convexos todas cuyas caras son regulares. ^[14] Existe primero en una serie de poliedros con simetría axial, por lo que también se le puede dar el nombre de girobianticúpula digonal .

Referencias

1. Holme, Audun (2010), Geometría: nuestro patrimonio cultural, Springer, doi :10.1007/978-3-642-14441-7, ISBN 978-3-642-14441-7.
2. Hartshorne, Robin (2000), Geometría: Euclides y más allá, Textos de pregrado en matemáticas, Springer-Verlag, p. 457, ISBN 9780387986500.
3. Timofeenko, AV (2009), "Los poliedros no compuestos no platónicos y no de Arquímedes", Journal of Mathematical Science , 162 (5): 725, doi :10.1007/s10958-009-9655-0, S2CID  120114341.
4. Montroll, John (2004), "Dodecadeltahedron", Una constelación de poliedros de origami , Dover Origami Papercraft Series, Dover Publications, Inc., págs. 38–40, ISBN 9780486439587.
5. Sloane, Nueva Jersey ; Hardin, RH; Duff, TDS; Conway, JH (1995), "Clústeres de esferas duras de energía mínima", Geometría discreta y computacional , 14 (3): 237–259, doi : 10.1007/BF02570704 , MR  1344734.
6. Cundy, H. Martyn (1952), "Deltahedra", The Mathematical Gazette , 36 (318): 263–266, doi :10.2307/3608204, JSTOR  3608204, MR  0051525, S2CID  250435684.
7. Francis, Darryl (agosto de 2013), "Sólidos de Johnson y sus siglas", Word Ways , 46 (3): 177
8. Berman, Martin (1971), "Poliedros convexos de caras regulares", Journal of the Franklin Institute , 291 (5): 329–352, doi :10.1016/0016-0032(71)90071-8, MR  0290245.
9. Lawson, Kyle A.; Parroquia, James L.; Traub, Cynthia M.; Weyhaupt, Adam G. (2013), "Colorear gráficos para clasificar geodésicas cerradas simples en deltaedros convexos". (PDF) , Revista Internacional de Matemáticas Puras y Aplicadas , 89 (2): 123–139, doi : 10.12732/ijpam.v89i2.1 , Zbl  1286.05048.
10. Arco de aleta, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2010), "Sobre triangulaciones bien cubiertas. III", Matemáticas aplicadas discretas , 158 (8): 894–912, doi : 10.1016/j.dam.2009.08.002 , MR  2602814.
11. Burdett, Jeremy K.; Hoffmann, Roald; Fay, Robert C. (1978), "Ocho coordinaciones", Química inorgánica , 17 (9): 2553–2568, doi :10.1021/ic50187a041.
12. Freudenthal, H .; van d. Waerden, BL (1947), "Sobre una afirmación de Euclides", Simon Stevin , 25 : 115–121, MR  0021687.
13. Bernal, JD (1964), "The Bakerian Lecture, 1962. The Structure of Liquids", Actas de la Royal Society of London , Serie A, Ciencias físicas y matemáticas, 280 (1382): 299–322, Bibcode :1964RSPSA. 280..299B, doi :10.1098/rspa.1964.0147, JSTOR  2415872, S2CID  178710030.
14. Johnson, Norman W. (1966), "Poliedros convexos con caras regulares", Canadian Journal of Mathematics , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR  0185507, S2CID  122006114, Zbl  0132.14603.

enlaces externos

• Weisstein, Eric W. "Desfenoide desaire". MundoMatemático .