
En teoría de grafos , un grafo bien cubierto es un grafo no dirigido en el que las coberturas mínimas de vértices tienen todas el mismo tamaño. Aquí, una cobertura de vértices es un conjunto de vértices que toca todas las aristas, y es mínima si al eliminar cualquier vértice de ella queda alguna arista sin cubrir. De manera equivalente, los grafos bien cubiertos son los grafos en los que todos los conjuntos independientes máximos tienen el mismo tamaño. Los grafos bien cubiertos fueron definidos y estudiados por primera vez por Michael D. Plummer en 1970.
Los grafos bien cubiertos incluyen todos los grafos completos , grafos bipartitos completos balanceados y los grafos de torre cuyos vértices representan cuadrados de un tablero de ajedrez y los bordes representan movimientos de una torre de ajedrez. Las caracterizaciones conocidas de los grafos cúbicos bien cubiertos, los grafos sin garras bien cubiertos y los grafos bien cubiertos de gran circunferencia permiten reconocer estos grafos en tiempo polinomial , pero probar si otros tipos de grafos están bien cubiertos es un problema coNP-completo .
Una cobertura de vértices en un grafo no dirigido es un conjunto de vértices que toca cada arista del grafo. Una cobertura de vértices es mínima, o irredundante, si eliminar cualquier vértice de ella destruiría la propiedad de cobertura: la eliminación haría que alguna arista quedara descubierta. Es mínima si no hay otra cobertura de vértices con menos vértices. Un grafo bien cubierto es aquel en el que cada cobertura mínima también es mínima. En el artículo original que define los grafos bien cubiertos, Plummer escribe que esto es "obviamente equivalente" a la propiedad de que cada dos coberturas mínimas tienen el mismo número de vértices entre sí. [1]
Un conjunto independiente en un grafo es un conjunto de vértices de los cuales ninguno de los dos es adyacente entre sí. Si C es una cubierta de vértices en un grafo G , el complemento de C debe ser un conjunto independiente, y viceversa. C es una cubierta de vértices mínima si y solo si su complemento I es un conjunto independiente maximal, y C es una cubierta de vértices mínima si y solo si su complemento es un conjunto independiente maximal. Por lo tanto, un grafo bien cubierto es, equivalentemente, un grafo en el que cada conjunto independiente maximal tiene el mismo tamaño, o un grafo en el que cada conjunto independiente maximal es máximo. [2]
En el artículo original que define los grafos bien cubiertos, estas definiciones se restringieron a los grafos conexos [3] , aunque también son significativas para los grafos desconectados. Algunos autores posteriores han reemplazado el requisito de conectividad con el requisito más débil de que un grafo bien cubierto no debe tener ningún vértice aislado [4] . Tanto para los grafos conexos bien cubiertos como para los grafos bien cubiertos sin vértices aislados, no puede haber vértices esenciales [ 4 ], vértices que pertenecen a cada cobertura mínima de vértices. Además, cada grafo bien cubierto es un grafo crítico para la cobertura de vértices en el sentido de que, para cada vértice v , eliminar v del grafo produce un grafo con una cobertura mínima de vértices más pequeña [3] .
El complejo de independencia de un grafo G es el complejo simplicial que tiene un símplice para cada conjunto independiente en G. Se dice que un complejo simplicial es puro si todos sus símplices máximos tienen la misma cardinalidad, por lo que un grafo bien cubierto es equivalentemente un grafo con un complejo de independencia puro. [5]
Un grafo de ciclo de longitud cuatro o cinco está bien cubierto: en cada caso, cada conjunto independiente máximo tiene tamaño dos. Un ciclo de longitud siete, y un camino de longitud tres, también están bien cubiertos. [6] Todo grafo completo está bien cubierto: cada conjunto independiente máximo consta de un único vértice. De manera similar, todo grafo de clúster (una unión disjunta de grafos completos) está bien cubierto. [7] Un grafo bipartito completo está bien cubierto si los dos lados de su bipartición tienen igual número de vértices, ya que estos son sus únicos dos conjuntos independientes máximos. El grafo complementario de un grafo sin triángulos sin vértices aislados está bien cubierto: no tiene conjuntos independientes mayores que dos, y cada vértice individual puede extenderse a un conjunto independiente de dos vértices. [6]
El grafo de una torre está bien cubierto: si uno coloca cualquier conjunto de torres en un tablero de ajedrez de manera que no haya dos torres atacándose entre sí, siempre es posible continuar colocando más torres no atacantes hasta que haya una en cada fila y columna del tablero de ajedrez. [8] El grafo cuyos vértices son las diagonales de un polígono simple y cuyos bordes conectan pares de diagonales que se cruzan entre sí está bien cubierto, porque sus conjuntos independientes máximos son triangulaciones del polígono y todas las triangulaciones tienen el mismo número de bordes. [9]
Si G es cualquier grafo de n vértices, entonces el producto raíz de G con un grafo de una arista (es decir, el grafo H formado añadiendo n nuevos vértices a G , cada uno de grado uno y cada uno adyacente a un vértice distinto en G ) está bien cubierto. Porque, un conjunto independiente maximal en H debe consistir en un conjunto independiente arbitrario en G junto con los vecinos de grado uno del conjunto complementario, y por lo tanto debe tener tamaño n . [10] De manera más general, dado cualquier grafo G junto con una cobertura de clique (una partición p de los vértices de G en cliques), el grafo G p formado añadiendo otro vértice a cada clique está bien cubierto; el producto raíz es el caso especial de esta construcción cuando p consiste en n cliques de un vértice. [11] Por lo tanto, cada grafo es un subgrafo inducido de un grafo bien cubierto.
Favaron (1982) define un grafo muy bien cubierto como un grafo bien cubierto (posiblemente desconectado, pero sin vértices aislados) en el que cada conjunto independiente máximo (y por lo tanto también cada cobertura mínima de vértices) contiene exactamente la mitad de los vértices. Esta definición incluye los productos raíz de un grafo G y un grafo de una arista. También incluye, por ejemplo, los grafos bipartitos bien cubiertos estudiados por Ravindra (1977) y Berge (1981): en un grafo bipartito sin vértices aislados, ambos lados de cualquier bipartición forman conjuntos independientes máximos (y coberturas mínimas de vértices), por lo que si el grafo está bien cubierto ambos lados deben tener la misma cantidad de vértices. En un grafo bien cubierto con n vértices, sin vértices aislados, el tamaño de un conjunto independiente máximo es como máximo n /2 , por lo que los grafos muy bien cubiertos son los grafos bien cubiertos en los que el tamaño máximo del conjunto independiente es lo más grande posible. [12]
Un grafo bipartito G está bien cubierto si y solo si tiene un emparejamiento perfecto M con la propiedad de que, para cada arista uv en M , el subgrafo inducido de los vecinos de u y v forma un grafo bipartito completo . [13] La caracterización en términos de emparejamientos se puede extender desde grafos bipartitos a grafos muy bien cubiertos: un grafo G está muy bien cubierto si y solo si tiene un emparejamiento perfecto M con las siguientes dos propiedades:
Además, si G está muy bien cubierto, entonces cada coincidencia perfecta en G satisface estas propiedades. [14]
Los árboles son un caso especial de grafos bipartitos, y comprobar si un árbol está bien cubierto puede manejarse como un caso especial mucho más simple de la caracterización de grafos bipartitos bien cubiertos: si G es un árbol con más de dos vértices, está bien cubierto si y solo si cada nodo no hoja del árbol es adyacente a exactamente una hoja. [13] La misma caracterización se aplica a grafos que son localmente similares a árboles, en el sentido de que los vecindarios de diámetro bajo de cada vértice son acíclicos: si un grafo tiene una circunferencia de ocho o más (de modo que, para cada vértice v , el subgrafo de vértices dentro de la distancia tres de v es acíclico) entonces está bien cubierto si y solo si cada vértice de grado mayor que uno tiene exactamente un vecino de grado uno. [15] Una caracterización estrechamente relacionada pero más compleja se aplica a grafos bien cubiertos de circunferencia de cinco o más. [16]


Los grafos cúbicos ( 3-regulares ) bien cubiertos se han clasificado: consisten en siete ejemplos 3-conectados , junto con tres familias infinitas de grafos cúbicos con menor conectividad. [17]
Los siete grafos cúbicos bien cubiertos 3-conexos son el grafo completo K 4 , los grafos del prisma triangular y del prisma pentagonal , el grafo de Durero , el grafo de utilidad K 3,3 , un grafo de ocho vértices obtenido a partir del grafo de utilidad mediante una transformada Y-Δ , y el grafo de Petersen generalizado de 14 vértices G (7,2) . [18] De estos grafos, los primeros cuatro son grafos planares . Son los únicos cuatro grafos poliédricos cúbicos (grafos de poliedros convexos simples ) que están bien cubiertos. [19] Cuatro de los grafos (los dos prismas, el grafo de Durero y G (7,2) ) son grafos de Petersen generalizados.
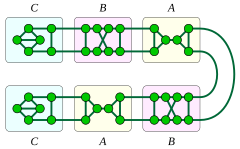
Los grafos cúbicos bien cubiertos 1- y 2-conectados se forman reemplazando los nodos de un camino o ciclo por tres fragmentos de grafos que Plummer (1993) etiqueta A , B y C . Los fragmentos A o B pueden usarse para reemplazar los nodos de un ciclo o los nodos interiores de un camino, mientras que el fragmento C se usa para reemplazar los dos nodos finales de un camino. El fragmento A contiene un puente , por lo que el resultado de realizar este proceso de reemplazo en un camino y usar el fragmento A para reemplazar algunos de los nodos del camino (y los otros dos fragmentos para los nodos restantes) es un grafo cúbico bien cubierto con 1 vértice conectado. Todos los grafos cúbicos bien cubiertos con 1 vértice conectado tienen esta forma, y todos estos grafos son planos. [17]
Existen dos tipos de grafos cúbicos bien cubiertos con 2 vértices conexos. Una de estas dos familias se forma reemplazando los nodos de un ciclo por fragmentos A y B , siendo al menos dos de los fragmentos del tipo A ; un grafo de este tipo es planar si y solo si no contiene ningún fragmento del tipo B . La otra familia se forma reemplazando los nodos de un camino por fragmentos del tipo B y C ; todos estos grafos son planares. [17]
Como complemento a la caracterización de los poliedros simples bien cubiertos en tres dimensiones, los investigadores también han considerado los poliedros simpliciales bien cubiertos , o equivalentemente los grafos planos maximales bien cubiertos. Todo grafo plano maximal con cinco o más vértices tiene conectividad de vértices 3, 4 o 5. [20] No hay grafos planos maximales 5-conectados bien cubiertos, y solo hay cuatro grafos planos maximales 4-conectados bien cubiertos: los grafos del octaedro regular , la bipirámide pentagonal , el disfenoide romo y un poliedro irregular (un deltaedro no convexo ) con 12 vértices, 30 aristas y 20 caras triangulares. Sin embargo, hay infinitos grafos planos maximales 3-conectados bien cubiertos. [21] Por ejemplo, si un grafo plano maximal de 3 t vértices tiene t caras triangulares disjuntas, entonces estas caras formarán una cubierta de clique. Por lo tanto, la construcción de cubierta de clique, que para estos grafos consiste en subdividir cada uno de estos t triángulos en tres nuevos triángulos que se encuentran en un vértice central, produce un grafo plano maximal bien cubierto. [22]
Probar si un gráfico contiene dos conjuntos independientes máximos de diferentes tamaños es NP-completo ; es decir, complementariamente, probar si un gráfico está bien cubierto es coNP-completo. [23] Aunque es fácil encontrar conjuntos independientes máximos en gráficos que se sabe que están bien cubiertos, también es NP-difícil para un algoritmo producir como salida, en todos los gráficos, ya sea un conjunto independiente máximo o una garantía de que la entrada no está bien cubierta. [24]
Por el contrario, es posible comprobar si un grafo dado G está muy bien cubierto en tiempo polinomial . Para ello, hay que encontrar el subgrafo H de G que consiste en las aristas que satisfacen las dos propiedades de una arista coincidente en un grafo muy bien cubierto y, a continuación, utilizar un algoritmo de coincidencia para comprobar si H tiene una coincidencia perfecta. [14] Algunos problemas que son NP-completos para grafos arbitrarios, como el problema de encontrar un ciclo hamiltoniano , también se pueden resolver en tiempo polinomial para grafos muy bien cubiertos. [25]
Se dice que un grafo es igualable si cada emparejamiento máximo es máximo; es decir, es igualable si su grafo lineal está bien cubierto. [26] Más fuertemente se dice que es igualable aleatoriamente si cada emparejamiento máximo es un emparejamiento perfecto . Los únicos grafos conexos que son igualables aleatoriamente son los grafos completos y los grafos bipartitos completos balanceados. [27] Es posible probar si un grafo lineal, o más generalmente un grafo sin garras , está bien cubierto en tiempo polinomial. [28]
Las caracterizaciones de gráficos bien cubiertos con circunferencia cinco o más, y de gráficos bien cubiertos que son 3-regulares, también conducen a algoritmos de tiempo polinomial eficientes para reconocer estos gráficos. [29]