Coordenadas de Rindler

Las coordenadas de Rindler son un sistema de coordenadas utilizado en el contexto de la relatividad especial para describir la aceleración hiperbólica de un sistema de referencia que se acelera uniformemente en el espacio-tiempo plano. En física relativista, las coordenadas de un sistema de referencia hiperbólicamente acelerado ^{[H 1] [1]} constituyen un gráfico de coordenadas importante y útil que representa parte del espacio-tiempo plano de Minkowski . ^{[2] [3] [4] [5]} En la relatividad especial , una partícula que se acelera uniformemente experimenta un movimiento hiperbólico , para el cual se puede elegir como su marco de referencia adecuado un marco de referencia que se acelera uniformemente en el que está en reposo . Los fenómenos en este marco hiperbólicamente acelerado pueden compararse con efectos que surgen en un campo gravitacional homogéneo . Para obtener una descripción general de las aceleraciones en el espacio-tiempo plano, consulte Aceleración (relatividad especial) y Marco de referencia adecuado (espacio-tiempo plano) .

En este artículo, la velocidad de la luz se define por c = 1 , las coordenadas inerciales son ( X , Y , Z , T ) y las coordenadas hiperbólicas son ( x , y , z , t ) . Estas coordenadas hiperbólicas se pueden separar en dos variantes principales dependiendo de la posición del observador acelerado: Si el observador está ubicado en el tiempo T = 0 en la posición X = 1/α (con α como la aceleración propia constante medida por un acelerómetro comovil ), entonces las coordenadas hiperbólicas a menudo se denominan coordenadas de Rindler con la métrica de Rindler correspondiente . ^[6] Si el observador está ubicado en el tiempo T = 0 en la posición X = 0 , entonces las coordenadas hiperbólicas a veces se denominan coordenadas de Møller ^[1] o coordenadas de Kottler-Møller con la correspondiente métrica de Kottler-Møller . ^[7] Un gráfico alternativo a menudo relacionado con observadores en movimiento hiperbólico se obtiene utilizando coordenadas de radar ^[8] que a veces se denominan coordenadas de Lass . ^{[9] [10]} Tanto las coordenadas de Kottler-Møller como las de Lass también se denominan coordenadas de Rindler. ^[11]

En cuanto a la historia, tales coordenadas se introdujeron poco después del advenimiento de la relatividad especial, cuando se estudiaron (total o parcialmente) junto con el concepto de movimiento hiperbólico: En relación con el espacio-tiempo plano de Minkowski por Albert Einstein (1907, 1912), ^{[H 2 ]} Max Born (1909), ^{[H 1]} Arnold Sommerfeld (1910), ^{[H 3]} Max von Laue (1911), ^{[H 4]} Hendrik Lorentz (1913), ^{[H 5]} Friedrich Kottler (1914), ^{[H 6]} Wolfgang Pauli (1921), ^{[H 7]} Karl Bollert (1922), ^{[H 8]} Stjepan Mohorovičić (1922), ^{[H 9]} Georges Lemaître (1924), ^{[H 10]} Einstein y Nathan Rosen (1935), ^{[H 2]} Christian Møller (1943, 1952), ^{[H 11]} Fritz Rohrlich (1963), ^[12] Harry Lass (1963), ^[13] y en relación con el espacio-tiempo plano y curvo de la relatividad general por Wolfgang Rindler ( 1960, 1966). ^{[14] [15]} Para obtener detalles y fuentes, consulte § Historia .

Características del marco Rindler

Gráfico de Rindler, en la ecuación ( 1a ), trazado en un diagrama de Minkowski. Las líneas discontinuas son los horizontes de Rindler. ${\displaystyle \alpha =0.5}$

La línea de mundo de un cuerpo en movimiento hiperbólico que tiene una aceleración adecuada constante en la dirección -en función del tiempo y la rapidez adecuados puede estar dada por ^[16] ${\displaystyle \alpha }$ ${\displaystyle X}$ ${\displaystyle \tau }$ ${\displaystyle \alpha \tau }$

${\displaystyle T=x\sinh(\alpha \tau ),\quad X=x\cosh(\alpha \tau )}$

donde es constante y variable, con la línea de mundo parecida a la hipérbola . Sommerfeld ^{[H 3] [17]} demostró que las ecuaciones pueden reinterpretarse definiéndolas como variables y constantes, de modo que representen la "forma en reposo" simultánea de un cuerpo en movimiento hiperbólico medida por un observador en movimiento. Al utilizar el tiempo propio del observador como el tiempo de todo el cuadro hiperbólicamente acelerado estableciendo , las fórmulas de transformación entre las coordenadas inerciales y las coordenadas hiperbólicas son en consecuencia: ^{[6] [9]} ${\displaystyle x=1/\alpha }$ ${\displaystyle \alpha \tau }$ ${\displaystyle X^{2}-T^{2}=x^{2}}$ ${\displaystyle x}$ ${\displaystyle \alpha \tau }$ ${\displaystyle \tau =t}$

con la inversa

${\displaystyle t={\frac {1}{\alpha }}\operatorname {artanh} \left({\frac {T}{X}}\right),\quad x={\sqrt {X^{2}-T^{2}}},\quad y=Y,\quad z=Z}$

Diferenciado e insertado en la métrica de Minkowski

${\displaystyle \mathrm {d} s^{2}=-\mathrm {d} T^{2}+\mathrm {d} X^{2}+\mathrm {d} Y^{2}+\mathrm {d} Z^{2},}$

la métrica en el marco hiperbólicamente acelerado sigue la siguiente

Estas transformaciones definen al observador de Rindler como un observador que está "en reposo" en las coordenadas de Rindler, es decir, que mantiene x , y , z constantes y sólo varía t a medida que pasa el tiempo. Las coordenadas son válidas en la región , que a menudo se llama cuña de Rindler , si representa la aceleración propia (a lo largo de la hipérbola ) del observador de Rindler cuyo tiempo propio se define como igual al tiempo de las coordenadas de Rindler. Para mantener esta línea mundial, el observador debe acelerar con una aceleración adecuada constante, y los observadores de Rindler más cercanos (al horizonte de Rindler) tienen una mayor aceleración adecuada. Todos los observadores de Rindler están instantáneamente en reposo en un momento en el marco inercial, y en ese momento un observador de Rindler con la aceleración adecuada estará en la posición (en realidad , pero asumimos unidades donde ), que también es la distancia constante de ese observador desde el horizonte de Rindler. en coordenadas Rindler. Si todos los observadores de Rindler ponen sus relojes a cero en , entonces al definir un sistema de coordenadas de Rindler tenemos la opción de elegir qué tiempo adecuado del observador de Rindler será igual al tiempo de coordenadas en coordenadas de Rindler, y la aceleración adecuada de este observador define el valor de arriba ( para otros observadores de Rindler a diferentes distancias del horizonte de Rindler, el tiempo coordinado será igual a algún múltiplo constante de su propio tiempo). ^[18] Es una convención común definir el sistema de coordenadas de Rindler de modo que el observador de Rindler cuyo tiempo adecuado coincida con el tiempo de coordenadas sea el que tenga la aceleración adecuada , de modo que pueda eliminarse de las ecuaciones. ${\displaystyle 0<X<\infty ,\;-X<T<X}$ ${\displaystyle \alpha }$ ${\displaystyle x=1/\alpha }$ ${\displaystyle x=0}$ ${\displaystyle T=0}$ ${\displaystyle \alpha _{i}}$ ${\displaystyle X=1/\alpha _{i}}$ ${\displaystyle X=c^{2}/\alpha _{i}}$ ${\displaystyle c=1}$ ${\displaystyle T=0}$ ${\displaystyle t}$ ${\displaystyle \alpha }$ ${\displaystyle \alpha =1}$ ${\displaystyle \alpha }$

La ecuación anterior se ha simplificado para . La ecuación no simplificada es más conveniente para encontrar la distancia del horizonte de Rindler, dada una aceleración . ${\displaystyle c=1}$ ${\displaystyle \alpha }$

${\displaystyle {\begin{aligned}&t={\frac {c}{\alpha }}\operatorname {artanh} \left({\frac {cT}{X}}\right)\;{\overset {X\,\gg \,cT}{\approx }}\;{\frac {c^{2}T}{\alpha X}}\\&\Rightarrow X\approx {\frac {c^{2}T}{\alpha t}}\;{\overset {T\,\approx \,t}{\approx }}\;{\frac {c^{2}}{\alpha }}\end{aligned}}}$

El resto del artículo seguirá la convención de establecer ambos y , por lo que las unidades para y serán 1 unidad . Tenga en cuenta que configurar segundos luz/segundo ² es muy diferente a configurar años luz/año ² . Incluso si elegimos unidades donde , la magnitud de la aceleración adecuada dependerá de nuestra elección de unidades: por ejemplo, si usamos unidades de años luz para la distancia, ( o ) y años para el tiempo, ( o ), esto significaría año luz/año ² , igual a aproximadamente 9,5 metros/segundo ² , mientras que si usamos unidades de segundos luz para distancia, ( o ), y segundos para tiempo, ( o ), esto significaría segundo luz/segundo ² , o 299 792 458 metros/segundo ² ). ${\displaystyle \alpha =1}$ ${\displaystyle c=1}$ ${\displaystyle X}$ ${\displaystyle x}$ ${\displaystyle =c^{2}/\alpha =1}$ ${\displaystyle \alpha =1}$ ${\displaystyle \alpha =1}$ ${\displaystyle c=1}$ ${\displaystyle \alpha }$ ${\displaystyle X}$ ${\displaystyle x}$ ${\displaystyle T}$ ${\displaystyle t}$ ${\displaystyle \alpha =1}$ ${\displaystyle X}$ ${\displaystyle x}$ ${\displaystyle T}$ ${\displaystyle t}$ ${\displaystyle \alpha =1}$

Variantes de fórmulas de transformación.

Se proporciona una derivación más general de las fórmulas de transformación cuando se formula la correspondiente tétrada de Fermi-Walker a partir de la cual se pueden derivar las coordenadas de Fermi o las coordenadas propias . ^[19] Dependiendo de la elección del origen de estas coordenadas, se puede derivar la métrica, la dilatación del tiempo entre el tiempo en el origen y en el punto , y la velocidad de la luz en coordenadas (esta velocidad variable de la luz no contradice la relatividad especial, porque es sólo un artefacto de las coordenadas aceleradas empleadas, mientras que en coordenadas inerciales permanece constante). En lugar de las coordenadas de Fermi, también se pueden utilizar las coordenadas de radar, que se obtienen determinando la distancia mediante señales luminosas (ver sección Conceptos de distancia), por lo que la métrica, la dilatación del tiempo y la velocidad de la luz ya no dependen de las coordenadas, en particular. , la velocidad coordinada de la luz sigue siendo idéntica a la velocidad de la luz en marcos inerciales: ${\displaystyle dt_{0}}$ ${\displaystyle dt}$ ${\displaystyle x}$ ${\displaystyle |dx|/|dt|}$ ${\displaystyle (c=1)}$

Los observadores de Rindler

En el nuevo gráfico ( 1a ) con y , es natural tomar el campo coframe ${\displaystyle c=1}$ ${\displaystyle \alpha =1}$

${\displaystyle d\sigma ^{0}=x\,dt,\;\;d\sigma ^{1}=dx,\;\;d\sigma ^{2}=dy,\;\;d\sigma ^{3}=dz}$

que tiene el campo de doble marco

${\displaystyle {\vec {e}}_{0}={\frac {1}{x}}\partial _{t},\;\;{\vec {e}}_{1}=\partial _{x},\;\;{\vec {e}}_{2}=\partial _{y},\;\;{\vec {e}}_{3}=\partial _{z}}$

Esto define un marco de Lorentz local en el espacio tangente en cada evento (en la región cubierta por nuestro diagrama de Rindler, es decir, la cuña de Rindler). Las curvas integrales del campo vectorial unitario temporal dan una congruencia temporal , que consiste en las líneas mundiales de una familia de observadores llamados observadores de Rindler . En el gráfico de Rindler, estas líneas mundiales aparecen como líneas de coordenadas verticales . Usando la transformación de coordenadas anterior, encontramos que corresponden a arcos hiperbólicos en la carta cartesiana original. ${\displaystyle {\vec {e}}_{0}}$ ${\displaystyle x=x_{0},\;y=y_{0},\;z=z_{0}}$

Algunos observadores representativos de Rindler (arcos hiperbólicos de color azul marino) representados utilizando la carta cartesiana. Las líneas rojas a 45 grados de la vertical representan el horizonte de Rindler; el sistema de coordenadas de Rindler sólo está definido a la derecha de este límite.

Como ocurre con cualquier congruencia temporal en cualquier variedad de Lorentz, esta congruencia tiene una descomposición cinemática (ver ecuación de Raychaudhuri ). En este caso, la expansión y la vorticidad de la congruencia de los observadores de Rindler desaparecen . La desaparición del tensor de expansión implica que cada uno de nuestros observadores mantiene una distancia constante con sus vecinos . La desaparición del tensor de vorticidad implica que las líneas mundiales de nuestros observadores no se retuercen entre sí; se trata de una especie de ausencia local de "remolinos".

El vector de aceleración de cada observador viene dado por la derivada covariante

${\displaystyle \nabla _{{\vec {e}}_{0}}{\vec {e}}_{0}={\frac {1}{x}}{\vec {e}}_{1}}$

Es decir, cada observador de Rindler acelera en la dirección. Hablando individualmente, cada observador está acelerando con magnitud constante en esta dirección, por lo que sus líneas mundiales son las análogas lorentzianas de los círculos, que son las curvas de curvatura de trayectoria constante en la geometría euclidiana. ${\displaystyle \partial _{x}}$

Debido a que los observadores de Rindler están libres de vorticidad , también son ortogonales de hipersuperficie . Los hiperslices espaciales ortogonales son ; estos aparecen como semiplanos horizontales en el diagrama de Rindler y como semiplanos en el diagrama cartesiano (consulte la figura anterior). Situando el elemento línea, vemos que estos tienen la geometría euclidiana ordinaria, . Por tanto, las coordenadas espaciales en la carta de Rindler tienen una interpretación muy simple consistente con la afirmación de que los observadores de Rindler son mutuamente estacionarios. Volveremos a esta propiedad de rigidez de los observadores de Rindler un poco más adelante en este artículo. ${\displaystyle t=t_{0}}$ ${\displaystyle T=X=0}$ ${\displaystyle dt=0}$ ${\displaystyle d\sigma ^{2}=dx^{2}+dy^{2}+dz^{2},\;\forall x>0,\forall y,z}$

Una propiedad "paradójica"

Tenga en cuenta que los observadores de Rindler con una coordenada x constante más pequeña están acelerando con más fuerza para mantener el ritmo. Esto puede parecer sorprendente porque en la física newtoniana los observadores que mantienen una distancia relativa constante deben compartir la misma aceleración. Pero en física relativista vemos que el extremo posterior de una varilla que es acelerada por alguna fuerza externa (paralela a su eje de simetría) debe acelerar un poco más que el extremo anterior, o de lo contrario finalmente debe romperse. Esta es una manifestación de la contracción de Lorentz . A medida que la varilla acelera, su velocidad aumenta y su longitud disminuye. Como se está acortando, la parte trasera debe acelerar más fuerte que la delantera. Otra forma de verlo es: la parte trasera debe lograr el mismo cambio de velocidad en un período de tiempo más corto. Esto conduce a una ecuación diferencial que muestra que, a cierta distancia, la aceleración del extremo posterior diverge, lo que da como resultado el horizonte de Rindler.

Este fenómeno es la base de una conocida "paradoja", la paradoja de la nave espacial de Bell . Sin embargo, es una simple consecuencia de la cinemática relativista. Una forma de ver esto es observar que la magnitud del vector de aceleración es simplemente la curvatura de la trayectoria de la línea mundial correspondiente. Pero las líneas del mundo de nuestros observadores de Rindler son análogas a una familia de círculos concéntricos en el plano euclidiano, por lo que simplemente estamos tratando con el análogo lorentziano de un hecho familiar para los patinadores de velocidad: en una familia de círculos concéntricos, los círculos internos deben doblarse. más rápido (por unidad de longitud de arco) que los exteriores .

Observadores de Minkowski

Un observador representativo de Minkowski (curva secante hiperbólica azul marino) representado utilizando el gráfico de Rindler. El horizonte de Rindler se muestra en rojo.

Vale la pena introducir también un marco alternativo, dado en la carta de Minkowski por la elección natural

${\displaystyle {\vec {f}}_{0}=\partial _{T},\;{\vec {f}}_{1}=\partial _{X},\;{\vec {f}}_{2}=\partial _{Y},\;{\vec {f}}_{3}=\partial _{Z}}$

Al transformar estos campos vectoriales usando la transformación de coordenadas dada anteriormente, encontramos que en el gráfico de Rindler (en la cuña de Rinder) este marco se convierte en

${\displaystyle {\begin{aligned}{\vec {f}}_{0}&={\frac {1}{x}}\cosh(t)\,\partial _{t}-\sinh(t)\,\partial _{x}\\{\vec {f}}_{1}&=-{\frac {1}{x}}\sinh(t)\,\partial _{t}+\cosh(t)\,\partial _{x}\\{\vec {f}}_{2}&=\partial _{y},\;{\vec {f}}_{3}=\partial _{z}\end{aligned}}}$

Calculando la descomposición cinemática de la congruencia temporal definida por el campo vectorial unitario temporal , encontramos que la expansión y la vorticidad nuevamente desaparecen, y además el vector de aceleración desaparece, . En otras palabras, se trata de una congruencia geodésica ; los observadores correspondientes están en un estado de movimiento inercial . En la carta cartesiana original, estos observadores, a quienes llamaremos observadores de Minkowski , están en reposo. ${\displaystyle {\vec {f}}_{0}}$ ${\displaystyle \nabla _{{\vec {f}}_{0}}{\vec {f}}_{0}=0}$

En el gráfico de Rindler, las líneas mundiales de los observadores de Minkowski aparecen como curvas secantes hiperbólicas asintóticas con respecto al plano de coordenadas . Específicamente, en coordenadas Rindler, la línea mundial del observador Minkowski que pasa por el evento es ${\displaystyle x=0}$ ${\displaystyle t=t_{0},\;x=x_{0},\;y=y_{0},\;z=z_{0}}$

${\displaystyle {\begin{aligned}t&=\operatorname {artanh} \left({\frac {s}{x_{0}}}\right),\;-x_{0}<s<x_{0}\\x&={\sqrt {x_{0}^{2}-s^{2}}},\;-x_{0}<s<x_{0}\\y&=y_{0}\\z&=z_{0}\end{aligned}}}$

¿ Dónde está el momento adecuado de este observador de Minkowski? Tenga en cuenta que sólo una pequeña parte de su historia está cubierta por el gráfico de Rindler. Esto muestra explícitamente por qué la carta de Rindler no está geodésicamente completa ; Las geodésicas temporales se extienden fuera de la región cubierta por la carta en un tiempo propio finito. Por supuesto, ya sabíamos que la carta de Rindler no puede ser geodésicamente completa, porque cubre sólo una parte de la carta cartesiana original, que es una carta geodésica completa. ${\displaystyle s}$

En el caso que se muestra en la figura, hemos dibujado (correctamente escalados y aumentados) los conos de luz en . ${\displaystyle x_{0}=1}$ ${\displaystyle s\in \left\{-{\frac {1}{2}},\;0,\;{\frac {1}{2}}\right\}}$

El horizonte de Rindler

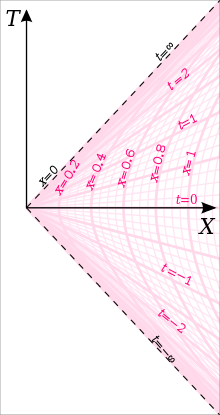
El gráfico de coordenadas de Rindler tiene una singularidad de coordenadas en x  = 0, donde el tensor métrico (expresado en las coordenadas de Rindler) tiene un determinante evanescente . Esto sucede porque cuando x  → 0 la aceleración de los observadores de Rindler diverge. Como podemos ver en la figura que ilustra la cuña de Rindler, el lugar geométrico x  = 0 en el diagrama de Rindler corresponde al lugar geométrico T ²  =  X ² ,  X  > 0 en el diagrama cartesiano, que consta de dos semiplanos nulos, cada uno regido por una congruencia geodésica nula.

Por el momento, simplemente consideramos el horizonte de Rindler como el límite de las coordenadas de Rindler. Si consideramos el conjunto de observadores acelerados que tienen una posición constante en coordenadas de Rindler, ninguno de ellos puede recibir señales luminosas de eventos con T  ≥  X (en el diagrama, estos serían eventos en o a la izquierda de la línea T = X , a lo largo del cual se encuentra el horizonte rojo superior; sin embargo, estos observadores podrían recibir señales de eventos con T  ≥  X si detuvieran su aceleración y cruzaran esta línea ellos mismos) ni podrían haber enviado señales a eventos con T  ≤ − X (eventos en o a la izquierda de la línea T = − X a lo largo de la cual se encuentra el horizonte rojo inferior; esos eventos se encuentran fuera de todos los conos de luz futuros de su línea de mundo pasado). Además, si consideramos a los miembros de este conjunto de observadores acelerados cada vez más cerca del horizonte, en el límite a medida que la distancia al horizonte se acerca a cero, la aceleración propia constante experimentada por un observador a esta distancia (que también sería la G- fuerza experimentada por tal observador) se acercaría al infinito. Ambos hechos también serían ciertos si estuviéramos considerando un conjunto de observadores flotando fuera del horizonte de sucesos de un agujero negro , cada observador flotando en un radio constante en coordenadas de Schwarzschild . De hecho, en las inmediaciones de un agujero negro, la geometría cercana al horizonte de sucesos se puede describir en coordenadas de Rindler. La radiación de Hawking en el caso de un marco acelerado se denomina radiación de Unruh . La conexión es la equivalencia de la aceleración con la gravitación.

Geodésicas

Las ecuaciones geodésicas de la carta de Rindler se obtienen fácilmente a partir del lagrangiano geodésico ; ellos son

${\displaystyle {\ddot {t}}+{\frac {2}{x}}\,{\dot {x}}\,{\dot {t}}=0,\;{\ddot {x}}+x\,{\dot {t}}^{2}=0,\;{\ddot {y}}=0,\;{\ddot {z}}=0}$

Por supuesto, en el mapa cartesiano original, las geodésicas aparecen como líneas rectas, por lo que podríamos obtenerlas fácilmente en el mapa de Rindler usando nuestra transformación de coordenadas. Sin embargo, es instructivo obtenerlos y estudiarlos independientemente del cuadro original, y así lo haremos en esta sección.

Algunas geodésicas nulas representativas (arcos semicirculares hiperbólicos negros) proyectadas en el hiperslice espacial t  = 0 de los observadores de Rindler. El horizonte de Rindler se muestra como un plano magenta.

De la primera, tercera y cuarta obtenemos inmediatamente las primeras integrales

${\displaystyle {\dot {t}}={\frac {E}{x^{2}}},\;\;{\dot {y}}=P,\;\;{\dot {z}}=Q}$

Pero a partir del elemento de línea tenemos dónde para geodésicas temporales, nulas y espaciales, respectivamente. Esto da la cuarta primera integral, es decir ${\displaystyle \varepsilon =-x^{2}\,{\dot {t}}^{2}+{\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}}$ ${\displaystyle \varepsilon \in \left\{-1,\,0,\,1\right\}}$

${\displaystyle {\dot {x}}^{2}=\left(\varepsilon +{\frac {E^{2}}{x^{2}}}\right)-P^{2}-Q^{2}}$.

Esto es suficiente para dar la solución completa de las ecuaciones geodésicas.

En el caso de geodésicas nulas , a partir de valores distintos de cero , vemos que la coordenada x se extiende a lo largo del intervalo ${\displaystyle {\frac {E^{2}}{x^{2}}}\,-\,P^{2}\,-\,Q^{2}}$ ${\displaystyle E}$

${\displaystyle 0\,<\,x\,<\,{\frac {E}{\sqrt {P^{2}\,+\,Q^{2}}}}}$.

La familia completa de siete parámetros que proporciona cualquier geodésica nula a través de cualquier evento en la cuña de Rindler es

${\displaystyle {\begin{aligned}t-t_{0}&=\operatorname {artanh} \left({\frac {1}{E}}\left[s\left(P^{2}+Q^{2}\right)-{\sqrt {E^{2}-\left(P^{2}+Q^{2}\right)x_{0}^{2}}}\right]\right)+\\&\qquad \operatorname {artanh} \left({\frac {1}{E}}{\sqrt {E^{2}-(P^{2}+Q^{2})x_{0}^{2}}}\right)\\x&={\sqrt {x_{0}^{2}+2s{\sqrt {E^{2}-(P^{2}+Q^{2})x_{0}^{2}}}-s^{2}(P^{2}+Q^{2})}}\\y-y_{0}&=Ps;\;\;z-z_{0}=Qs\end{aligned}}}$

Al trazar las trayectorias de algunas geodésicas nulas representativas a través de un evento determinado (es decir, proyectarlas al hipercorte ), obtenemos una imagen que se parece sospechosamente a la familia de todos los semicírculos que pasan por un punto y son ortogonales al horizonte de Rindler (consulte la figura). ^[27] ${\displaystyle t=0}$

La métrica de Fermat

El hecho de que en el gráfico de Rindler, las proyecciones de geodésicas nulas en cualquier hipercorte espacial para los observadores de Rindler sean simplemente arcos semicirculares se puede verificar directamente a partir de la solución general que se acaba de dar, pero hay una manera muy sencilla de verlo. Un espacio-tiempo estático es aquel en el que se puede encontrar un campo vectorial Killing similar al tiempo libre de vorticidad. En este caso, tenemos una familia definida de forma única de hipercortes espaciales (idénticos) ortogonales a los observadores estáticos correspondientes (que no necesitan ser observadores inerciales). Esto nos permite definir una nueva métrica en cualquiera de estos hiperslices que esté relacionada conformemente con la métrica original heredada del espacio-tiempo, pero con la propiedad de que la geodésica en la nueva métrica (tenga en cuenta que esta es una métrica de Riemann en una triple variedad de Riemann) son precisamente las proyecciones de las geodésicas nulas del espaciotiempo. Esta nueva métrica se llama métrica de Fermat , y en un espacio-tiempo estático dotado de un gráfico de coordenadas en el que el elemento lineal tiene la forma

${\displaystyle ds^{2}=g_{00}\,dt^{2}+g_{jk}\,dx^{j}\,dx^{k},\;\;j,\;k\in \{1,2,3\}}$

la métrica de Fermat es simplemente ${\displaystyle t=0}$

${\displaystyle d\rho ^{2}={\frac {1}{-g_{00}}}\left(g_{jk}\,dx^{j}\,dx^{k}\right)}$

(donde se entiende que los coeficientes métricos se evalúan en ). ${\displaystyle t=0}$

En el diagrama de Rindler, la traducción temporal es un campo vectorial Killing, por lo que se trata de un espaciotiempo estático (no es sorprendente, ya que el espaciotiempo de Minkowski es, por supuesto, trivialmente una solución estática de vacío de la ecuación de campo de Einstein ). Por lo tanto, podemos escribir inmediatamente la métrica de Fermat para los observadores de Rindler: ${\displaystyle \partial _{t}}$

${\displaystyle d\rho ^{2}={\frac {1}{x^{2}}}\left(dx^{2}+dy^{2}+dz^{2}\right),\;\;\forall x>0,\;\;\forall y,z}$

Pero este es el conocido elemento lineal del hiperbólico H ³ de tres espacios en el gráfico del medio espacio superior . Esto es muy análogo al conocido gráfico del semiplano superior para el plano hiperbólico H ² , que es familiar para generaciones de estudiantes de análisis complejos en relación con problemas de mapeo conforme (y mucho más), y muchos lectores con mentalidad matemática ya saben que las geodésicas de H ² en el modelo del semiplano superior son simplemente semicírculos (ortogonales al círculo en el infinito representado por el eje real).

Simetrías

Dado que el gráfico de Rindler es un gráfico de coordenadas para el espacio-tiempo de Minkowski, esperamos encontrar diez campos vectoriales Killing linealmente independientes. De hecho, en el gráfico cartesiano podemos encontrar fácilmente diez campos vectoriales Killing linealmente independientes, que generan respectivamente un subgrupo de parámetros de traducción temporal , tres espaciales, tres rotaciones y tres impulsos. Juntos generan el grupo de Poincaré (isócrono propio), el grupo de simetría del espacio-tiempo de Minkowski.

Sin embargo, es instructivo escribir y resolver las ecuaciones del vector Killing directamente. Obtenemos cuatro campos vectoriales Killing de aspecto familiar.

${\displaystyle \partial _{t},\;\;\partial _{y},\;\;\partial _{z},\;\;-z\,\partial _{y}+y\,\partial _{z}}$

(traslación temporal, traslaciones espaciales ortogonales a la dirección de aceleración y rotación espacial ortogonal a la dirección de aceleración) más seis más:

${\displaystyle {\begin{aligned}&\exp(\pm t)\,\left({\frac {y}{x}}\,\partial _{t}\pm \left[y\,\partial _{x}-x\,\partial _{y}\right]\right)\\&\exp(\pm t)\,\left({\frac {z}{x}}\,\partial _{t}\pm \left[z\,\partial _{x}-x\,\partial _{z}\right]\right)\\&\exp(\pm t)\,\left({\frac {1}{x}}\,\partial _{t}\pm \partial _{x}\right)\end{aligned}}}$

(donde los signos se eligen consistentemente + o -). Lo dejamos como ejercicio para descubrir cómo se relacionan estos con los generadores estándar; Aquí deseamos señalar que debemos poder obtener generadores equivalentes a los de la carta cartesiana, aunque la cuña de Rindler obviamente no es invariante según esta traducción. ¿Cómo puede ser esto? La respuesta es que, como cualquier cosa definida por un sistema de ecuaciones diferenciales parciales en una variedad suave, la ecuación de Killing en general tendrá soluciones definidas localmente, pero es posible que no existan globalmente. Es decir, con restricciones adecuadas en el parámetro de grupo, siempre se puede definir un flujo Killing en una vecindad local adecuada , pero es posible que el flujo no esté bien definido globalmente . Esto no tiene nada que ver con las variedades de Lorentz per se, ya que surge el mismo problema en el estudio de las variedades suaves generales . ${\displaystyle \partial _{T}}$

Nociones de distancia

Una de las muchas lecciones valiosas que se pueden aprender del estudio de la carta de Rindler es que, de hecho, existen varias nociones distintas (pero razonables) de distancia que pueden utilizar los observadores de Rindler.

Significado operativo de la distancia del radar entre dos observadores Rindler (líneas verticales de color azul marino). El horizonte de Rindler se muestra a la izquierda (línea vertical roja). También se representa la línea mundial del pulso del radar, junto con los conos de luz (con la escala adecuada) en los eventos A, B, C.

La primera es la que hemos empleado tácitamente anteriormente: la métrica de Riemann inducida en los hiperslices espaciales . A esto lo llamaremos distancia de regla ya que corresponde a esta métrica de Riemann inducida, pero su significado operativo puede no ser evidente de inmediato. ${\displaystyle t=t_{0}}$

Desde el punto de vista de la medición física, una noción más natural de distancia entre dos líneas mundiales es la distancia del radar . Esto se calcula enviando una geodésica nula desde la línea mundial de nuestro observador (evento A) a la línea mundial de algún objeto pequeño, tras lo cual se refleja (evento B) y regresa al observador (evento C). La distancia del radar se obtiene entonces dividiendo el tiempo de viaje de ida y vuelta, medido por un reloj ideal que lleva nuestro observador.

(Afortunadamente, en el espacio-tiempo de Minkowski podemos ignorar la posibilidad de múltiples caminos geodésicos nulos entre dos líneas mundiales, pero en los modelos cosmológicos y otras aplicaciones ^{[¿ cuáles? ]} las cosas no son tan simples. También debemos advertir que no se debe suponer que esta noción de distancia entre dos observadores da una noción que es simétrica al intercambiar los observadores.)

En particular, considere un par de observadores Rindler con coordenadas y respectivamente. (Tenga en cuenta que el primero de ellos, el observador que va detrás, está acelerando un poco más para poder seguir el ritmo del observador que va delante). Si utilizamos el elemento de línea de Rindler, obtenemos fácilmente la ecuación de geodésicas nulas que se mueven en la dirección de la aceleración: ${\displaystyle x=x_{0},\;y=0,\;z=0}$ ${\displaystyle x=x_{0}+h,\;y=0,\;z=0}$ ${\displaystyle dy=dz=0}$

${\displaystyle t-t_{0}=\log \left({\frac {x}{x_{0}}}\right)}$

Por lo tanto, la distancia del radar entre estos dos observadores está dada por

${\displaystyle x_{0}\,\log \left(1+{\frac {h}{x_{0}}}\right)=h-{\frac {h^{2}}{2\,x_{0}}}+O\left(h^{3}\right)}$

Esta es un poco menor que la distancia de la regla, pero para los observadores cercanos la discrepancia es insignificante.

Una tercera noción posible de distancia es la siguiente: nuestro observador mide el ángulo subtendido por un disco unitario colocado sobre algún objeto (no un objeto puntual), tal como aparece desde su ubicación. A esto lo llamamos distancia del diámetro óptico . Debido al carácter simple de las geodésicas nulas en el espacio-tiempo de Minkowski, podemos determinar fácilmente la distancia óptica entre nuestro par de observadores Rindler (alineados con la dirección de la aceleración). A partir de un boceto, debería ser plausible que la distancia del diámetro óptico aumente como . Por lo tanto, en el caso de un observador rezagado que estima la distancia a un observador líder (el caso ), la distancia óptica es un poco mayor que la distancia de la regla, que es un poco mayor que la distancia del radar. El lector debería ahora tomarse un momento para considerar el caso de un observador líder que estima la distancia a un observador que se encuentra detrás. ${\textstyle h+{\frac {1}{x_{0}}}+O\left(h^{3}\right)}$ ${\displaystyle h>0}$

Hay otras nociones de distancia, pero el punto principal es claro: si bien los valores de estas diversas nociones en general no estarán de acuerdo para un par determinado de observadores de Rindler, todos coinciden en que cada par de observadores de Rindler mantiene una distancia constante . El hecho de que los observadores de Rindler muy cercanos sean mutuamente estacionarios se deriva del hecho, mencionado anteriormente, de que el tensor de expansión de la congruencia de Rindler desaparece de manera idéntica. Sin embargo, hemos demostrado aquí que, en varios sentidos, esta propiedad de rigidez se mantiene en escalas mayores. Esta es verdaderamente una propiedad de rigidez notable, dado el hecho bien conocido de que en la física relativista ninguna varilla puede acelerarse rígidamente (y ningún disco puede girar rígidamente ), al menos no sin sufrir tensiones no homogéneas. La forma más sencilla de ver esto es observar que en la física newtoniana, si "pateamos" un cuerpo rígido, todos los elementos de materia del cuerpo cambiarán inmediatamente su estado de movimiento. Por supuesto, esto es incompatible con el principio relativista de que ninguna información que tenga algún efecto físico puede transmitirse más rápido que la velocidad de la luz.

De ello se deduce que si una barra es acelerada por alguna fuerza externa aplicada en cualquier lugar a lo largo de su longitud, los elementos de materia en varios lugares diferentes de la barra no pueden sentir todos la misma magnitud de aceleración si la barra no se extiende sin límite y finalmente se rompe. En otras palabras, una varilla acelerada que no se rompe debe soportar tensiones que varían a lo largo de su longitud. Además, en cualquier experimento mental con fuerzas que varían en el tiempo, ya sea que "pateemos" un objeto o intentemos acelerarlo gradualmente, no podemos evitar el problema de evitar modelos mecánicos que son inconsistentes con la cinemática relativista (porque partes distantes del cuerpo responden demasiado rápido). a una fuerza aplicada).

Volviendo a la cuestión del significado operativo de la distancia de la regla, vemos que ésta debería ser la distancia que nuestros observadores obtendrían si pasaran muy lentamente de mano en mano una pequeña regla que se coloca repetidamente de un extremo a otro. Pero justificar en detalle esta interpretación requeriría algún tipo de modelo material.

Generalización a espacios-tiempos curvos.

Las coordenadas de Rindler descritas anteriormente se pueden generalizar al espacio-tiempo curvo, como coordenadas normales de Fermi . La generalización implica esencialmente construir una tétrada ortonormal apropiada y luego transportarla a lo largo de la trayectoria dada utilizando la regla de transporte de Fermi-Walker . Para más detalles, consulte el artículo de Ni y Zimmermann en las referencias siguientes. En realidad, tal generalización permite estudiar los efectos inerciales y gravitacionales en un laboratorio terrestre, así como los efectos acoplados inercial-gravitacionales, más interesantes.

Historia

Descripción general

Coordenadas Kottler-Møller y Rindler

Albert Einstein (1907) ^{[H 13]} estudió los efectos dentro de un marco uniformemente acelerado, obteniendo ecuaciones para la dilatación del tiempo dependiente de las coordenadas y la velocidad de la luz equivalentes a ( 2c ), y para independizar las fórmulas del origen del observador, obtuvo dilatación del tiempo ( 2i ) de acuerdo formal con las coordenadas del radar. Al introducir el concepto de rigidez de Born , Max Born (1909) ^{[H 14]} señaló que las fórmulas para el movimiento hiperbólico pueden usarse como transformaciones en un "sistema de referencia hiperbólicamente acelerado" ( alemán : hyperbolisch beschleunigtes Bezugsystem ) equivalente a ( 2d ). El trabajo de Born fue elaborado aún más por Arnold Sommerfeld (1910) ^{[H 15]} y Max von Laue (1911) ^{[H 16]} quienes obtuvieron ( 2d ) usando números imaginarios , lo cual fue resumido por Wolfgang Pauli (1921) ^[16] quien además Las coordenadas ( 2d ) también se obtienen en la métrica ( 2e ) usando números imaginarios. Einstein (1912) ^{[H 17]} estudió un campo gravitacional estático y obtuvo la métrica de Kottler-Møller ( 2b ), así como aproximaciones a las fórmulas ( 2a ), utilizando una velocidad de la luz dependiente de las coordenadas. ^[28] Hendrik Lorentz (1913) ^{[H 18]} obtuvo coordenadas similares a ( 2d , 2e , 2f ) mientras estudiaba el principio de equivalencia de Einstein y el campo gravitacional uniforme.

Friedrich Kottler (1914), ^{[H 19]} dio una descripción detallada, quien formuló la tétrada ortonormal correspondiente , las fórmulas de transformación y la métrica ( 2a , 2b ). También Karl Bollert (1922) ^{[H 20]} obtuvo la métrica ( 2b ) en su estudio de la aceleración uniforme y los campos gravitacionales uniformes. En un artículo sobre la rigidez de Born, Georges Lemaître (1924) ^{[H 21]} obtuvo coordenadas y métrica ( 2a , 2b ). Albert Einstein y Nathan Rosen (1935) describieron ( 2d , 2e ) como las expresiones "bien conocidas" para un campo gravitacional homogéneo. ^{[H 22]} Después de que Christian Møller (1943) ^{[H 11]} obtuviera ( 2a , 2b ) en un estudio relacionado con campos gravitacionales homogéneos, él (1952) ^{[H 23]} así como Misner & Thorne & Wheeler (1973) ^{[2 ]} utilizó el transporte de Fermi-Walker para obtener las mismas ecuaciones.

Si bien estas investigaciones se centraban en el espacio-tiempo plano, Wolfgang Rindler (1960) ^[14] analizó el movimiento hiperbólico en el espacio-tiempo curvo y mostró (1966) ^[15] la analogía entre las coordenadas hiperbólicas ( 2d , 2e ) en el espacio-tiempo plano con las coordenadas de Kruskal en Espacio de Schwarzschild . Esto influyó en los escritores posteriores en su formulación de la radiación de Unruh medida por un observador en movimiento hiperbólico, que es similar a la descripción de Hawking de la radiación de los agujeros negros .

Horizonte

Born (1909) demostró que los puntos internos de un cuerpo rígido de Born en movimiento hiperbólico sólo pueden estar en la región . ^{[H 24]} Sommerfeld (1910) definió que las coordenadas permitidas para la transformación entre coordenadas inerciales e hiperbólicas deben satisfacer . ^{[H 25]} Kottler (1914) ^{[H 26]} definió esta región como y señaló la existencia de un "plano fronterizo" ( en alemán : Grenzebene ) , más allá del cual ninguna señal puede llegar al observador en movimiento hiperbólico. Esto fue llamado el "horizonte del observador" ( en alemán : Horizont des Beobachters ) por Bollert (1922). ^{[H 27]} Rindler (1966) ^[15] demostró la relación entre dicho horizonte y el horizonte en coordenadas Kruskal. ${\displaystyle X/\left(X^{2}-T^{2}\right)>0}$ ${\displaystyle T<X}$ ${\displaystyle X^{2}-T^{2}>0}$ ${\displaystyle c^{2}/\alpha +x}$

Coordenadas radar

Utilizando el formalismo de Bollert, Stjepan Mohorovičić (1922) ^{[H 28]} hizo una elección diferente para algún parámetro y obtuvo la métrica ( 2h ) con un error de impresión, que fue corregida por Bollert (1922b) con otro error de impresión, hasta obtener una versión sin error de impresión. fue dada por Mohorovičić (1923). Además, Mohorovičić argumentó erróneamente que la métrica ( 2b , ahora llamada métrica de Kottler-Møller) es incorrecta, lo que fue refutado por Bollert (1922). ^{[H 29]} La métrica ( 2h ) fue redescubierta por Harry Lass (1963), ^[13] quien también dio las coordenadas correspondientes ( 2g ), que a veces se denominan "coordenadas de Lass". ^[9] La métrica ( 2h ), así como ( 2a , 2b ), también fue derivada por Fritz Rohrlich (1963). ^[12] Finalmente, las coordenadas de Lass ( 2g , 2h ) fueron identificadas con coordenadas de radar por Desloge y Philpott (1987). ^{[29] [8]}

Tabla con fórmulas históricas.

Ver también

• La paradoja de la nave espacial de Bell , para un tema a veces controvertido que a menudo se estudia utilizando las coordenadas de Rindler.
• Coordenadas nacidas , para otro importante sistema de coordenadas adaptado al movimiento de ciertos observadores acelerados en el espacio-tiempo de Minkowski .
• Congruencia (relatividad general)
• Paradoja de Ehrenfest , para un tema a veces controvertido que a menudo se estudia utilizando las coordenadas de Born.
• Campos de marco en relatividad general
• Recursos de relatividad general
• modelo milne
• Ecuación de Raychaudhuri
• efecto desenfrenado

Referencias

1. Øyvind Grøn (2010). Apuntes de conferencias sobre la teoría general de la relatividad . Apuntes de conferencias de física. vol. 772. Saltador. págs. 86–91. ISBN 978-0387881348.
2. Misner, CW; Thorne, KS; Wheeler, JA (1973). Gravitación . Hombre libre. ISBN 0716703440.
3. Kopeikin, S., Efroimsky, M., Kaplan, G. (2011). Mecánica Celeste Relativista del Sistema Solar . John Wiley e hijos. ISBN 978-3527408566.{{cite book}}: CS1 maint: multiple names: authors list (link)
4. Padmanabhan, T. (2010). Gravitación: fundamentos y fronteras . Prensa de la Universidad de Cambridge. ISBN 978-1139485395.
5. ND Birrell, PCW Davies (1982). Campos cuánticos en el espacio curvo . Prensa de la Universidad de Cambridge. ISBN 1107392810.
6. Leonard Susskind, James Lindesay (2005). Introducción a los agujeros negros, la información y la revolución de la teoría de cuerdas: el universo holográfico . Científico mundial. págs. 8-10. ISBN 9812561315.
7. Muñoz, Gerardo; Jones, Preston (2010). "El principio de equivalencia, los marcos de referencia uniformemente acelerados y el campo gravitacional uniforme". Revista Estadounidense de Física . 78 (4): 377–383. arXiv : 1003.3022 . Código Bib : 2010AmJPh..78..377M. doi : 10.1119/1.3272719. S2CID  118616525.
8. Minguzzi, E. (2005). "La métrica de Minkowski en coordenadas de radar de observador no inercial". Revista Estadounidense de Física . 73 (12): 1117-1121. arXiv : física/0412024 . Código bibliográfico : 2005AmJPh..73.1117M. doi : 10.1119/1.2060716. S2CID  119359878.
9. David Tilbrook (1997). "Coordinaciones generales del espacio-tiempo plano de aceleración propia constante". Revista Australiana de Física . 50 (5): 851–868. doi : 10.1071/P96111 .
10. Jones, Preston; Wanex, Lucas F. (2006). "La paradoja del reloj en un campo gravitacional estático homogéneo". Fundamentos de Letras de Física . 19 (1): 75–85. arXiv : física/0604025 . Código bibliográfico : 2006FoPhL..19...75J. doi :10.1007/s10702-006-1850-3. S2CID  14583590.
11. Por ejemplo, Birrell & Davies (1982), págs. 110-111 o Padmanabhan (2010), pág. 126 denotan ecuaciones ( 2g , 2h ) como coordenadas de Rindler o marco de Rindler; Tilbrook (1997) págs. 864–864 o Jones y Wanex (2006) denotan las ecuaciones ( 2a , 2b ) como coordenadas de Rindler
12. Rohrlich, Fritz (1963). "El principio de equivalencia". Anales de Física . 22 (2): 169-191. Código bibliográfico : 1963AnPhy..22..169R. doi :10.1016/0003-4916(63)90051-4.
13. Harry Lass (1963). "Aceleración de los marcos de referencia y la paradoja del reloj". Revista Estadounidense de Física . 31 (4): 274–276. Código bibliográfico : 1963AmJPh..31..274L. doi :10.1119/1.1969430. S2CID  121608504.
14. Rindler, W. (1960). "Movimiento hiperbólico en el espacio-tiempo curvo". Revisión física . 119 (6): 2082–2089. Código bibliográfico : 1960PhRv..119.2082R. doi : 10.1103/PhysRev.119.2082.
15. Rindler, W. (1966). "El espacio Kruskal y el marco uniformemente acelerado". Revista Estadounidense de Física . 34 (12): 1174-1178. Código bibliográfico : 1966AmJPh..34.1174R. doi :10.1119/1.1972547.
16. Pauli, Wolfgang (1921), "Die Relativitätstheorie", Encyclopädie der Mathematischen Wissenschaften , 5 (2): 539–776
    En inglés: Pauli, W. (1981) [1921]. Teoría de la relatividad . vol. 165. Publicaciones de Dover. ISBN 0-486-64152-X. {{cite book}}: |journal=ignorado ( ayuda )
17. von Laue, M. (1921). Die Relativitätstheorie, Band 1 (cuarta edición de "Das Relativitätsprinzip" ed.). Vereg.; Primera edición 1911, segunda edición ampliada 1913, tercera edición ampliada 1919.
18. Don Koks (2006). Exploraciones en Física Matemática . Saltador. págs. 235–269. ISBN 0387309438.
19. Moller, C. (1955) [1952]. La teoría de la relatividad. Prensa de Oxford Clarendon.
20. Møller (1952), ecuación. 154
21. Misner & Thorne & Wheeler (1973), sección 6.6
22. Muñoz y Jones (2010), ecuación. 37, 38
23. Pauli (1921), sección 32-y
24. Rindler (1966), pág. 1177
25. Massimo Pauri, Michele Vallisneri (2000). "Coordenadas de Märzke-Wheeler para observadores acelerados en relatividad especial". Fundamentos de Letras de Física . 13 (5): 401–425. arXiv : gr-qc/0006095 . Código Bib : 2000gr.qc.....6095P. doi :10.1023/A:1007861914639. S2CID  15097773.
26. Dolby, Carl E.; Gaviota, Stephen F. (2001). "En el radar el tiempo y la "paradoja" de los gemelos". Revista Estadounidense de Física . 69 (12): 1257–1261. arXiv : gr-qc/0104077 . Bibcode : 2001AmJPh..69.1257D. doi : 10.1119/1.1407254. S2CID  119067219.
27. Rouaud, Mathieu (11 de agosto de 2022). "El ascensor de Einstein: líneas del mundo, experimento de Michelson-Morley y paradoja relativista". Física . 4 (3): 892–911. doi : 10.3390/física4030058 . S2CID  236427014.
28. Blum, AS, Renn, J., Salisbury, DC, Schemmel, M. y Sundermeyer, K. (2012). "1912: un punto de inflexión en el camino de Einstein hacia la relatividad general". Annalen der Physik . 524 (1): A12-A13. Código Bib : 2012AnP...524A..11B. doi : 10.1002/andp.201100705. S2CID  123564577.{{cite journal}}: CS1 maint: multiple names: authors list (link)
29. Desloge, Edward A.; Philpott, RJ (1987). "Marcos de referencia uniformemente acelerados en relatividad especial". Revista Estadounidense de Física . 55 (3): 252–261. Código bibliográfico : 1987AmJPh..55..252D. doi :10.1119/1.15197.
30. Herglotz (1909), págs.408, 414

Fuentes históricas

1. Nacido, Max (1909). "Die Theorie des starren Elektrons in der Kinematik des Relativitätsprinzips" [traducción de Wikisource: La teoría del electrón rígido en la cinemática del principio de relatividad]. Annalen der Physik . 335 (11): 1–56. Código bibliográfico : 1909AnP...335....1B. doi : 10.1002/andp.19093351102.
2. Einstein, Albert (1908) [1907], "Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen" (PDF) , Jahrbuch der Radioaktivität und Elektronik , 4 : 411–462, Bibcode : 1908JRE..... 4.. 411E; Traducción al inglés Sobre el principio de la relatividad y las conclusiones extraídas de él en el proyecto en papel de Einstein. Einstein, Albert (1912), "Lichtgeschwindigkeit und Statik des Gravitationsfeldes", Annalen der Physik , 343 (7): 355–369, Bibcode :1912AnP...343..355E, doi :10.1002/andp.19123430704, traducción al inglés Proyecto en papel La velocidad de la luz y la estática del campo gravitacional en Einstein.
3. Sommerfeld, Arnold (1910). "Zur Relativitätstheorie II: Vierdimensionale Vektoranalysis" [traducción de Wikisource: Sobre la teoría de la relatividad II: análisis de vectores cuatridimensionales]. Annalen der Physik . 338 (14): 649–689. Código bibliográfico : 1910AnP...338..649S. doi : 10.1002/andp.19103381402.
4. Laue, Max von (1911). Das Relativitätsprinzip. Braunschweig: Vieweg.
5. Lorentz, Hendrik Antoon (1914) [1913]. Das Relativitätsprinzip. Drei Vorlesungen gehalten en Teylers Stiftung zu Haarlem (1913)  . Leipzig/Berlín: BG Teubner.
6. Kottler, Friedrich (1912). "Über die Raumzeitlinien der Minkowski'schen Welt" [Traducción de Wikisource: Sobre las líneas espacio-temporales de un mundo Minkowski]. Wiener Sitzungsberichte 2a . 121 : 1659-1759. hdl :2027/mdp.39015051107277.Kottler, Friedrich (1914a). "Relativitätsprinzip und beschleunigte Bewegung". Annalen der Physik . 349 (13): 701–748. Código bibliográfico : 1914AnP...349..701K. doi : 10.1002/andp.19143491303.Kottler, Friedrich (1914b). "Fallende Bezugssysteme vom Standpunkte des Relativitätsprinzips". Annalen der Physik . 350 (20): 481–516. Código bibliográfico : 1914AnP...350..481K. doi : 10.1002/andp.19143502003.Kottler, Friedrich (1916). "Über Einsteins Äquivalenzhypothese und die Gravitation". Annalen der Physik . 355 (16): 955–972. Código bibliográfico : 1916AnP...355..955K. doi : 10.1002/andp.19163551605.Kottler, Friedrich (1918). "Über die physikalischen Grundlagen der Einsteinschen Relativitätstheorie". Annalen der Physik . 361 (14): 401–461. Código Bib : 1918AnP...361..401K. doi : 10.1002/andp.19183611402.
7. Pauli, W. (1921). "La teoría de la relatividad". Encyclopädie der mathematischen Wissenschaften . vol. 5. Leipzig, BG Teubner. págs. 539–776.Nueva edición 2013: Editor: Domenico Giulini, Springer, 2013 ISBN 3642583555 . 
8. Karl Bollert (1922a). "Das homogene Gravitationsfeld und die Lorentztransformationen". Zeitschrift für Physik . 10 (1): 256–266. Código bibliográfico : 1922ZPhy...10..256B. doi :10.1007/BF01332567. S2CID  122965400.Karl Bollert (1922b). "Die Entstehung der Lorentzverkürzung und die strenge Behandlung des Uhrenparadoxons". Zeitschrift für Physik . 12 (1): 189–206. Código Bib : 1923ZPhy...12..189B. doi :10.1007/BF01328090. S2CID  120603392.
9. Mohorovičić, S. (1922). "Das" homogene "Gravitationsfeld und die Lorentztransformation". Zeitschrift für Physik . 11 (1): 88–92. Código bibliográfico : 1922ZPhy...11...88M. doi :10.1007/BF01328404. S2CID  123661029.Mohorovičić, S. (1923). "Äther, Materie, Gravitation und Relativitätstheorie". Zeitschrift für Physik . 18 (1): 34–63. Código Bib : 1923ZPhy...18...34M. doi :10.1007/BF01327684. S2CID  123728700.
10. Lemaître, G. (1924), "El movimiento de un sólido rígido según el principio de la relatividad", Revista Filosófica , Serie 6, 48 (283): 164–176, doi :10.1080/14786442408634478
11. Møller, C. (1943). "Sobre campos gravitacionales homogéneos en la teoría general de la relatividad y la paradoja del reloj". Dan. Estera. Fys. Med . . 8 : 3–25.Møller, C. (1955) [1952]. La teoría de la relatividad. Prensa de Oxford Clarendon.
12. Kottler (1914b), págs. 488-489, 492-493
13. Einstein, Alberto; Rosen, Nathan (1935). "Un problema de partículas en la teoría general de la relatividad". Revisión física . 48 (1): 73–77. Código bibliográfico : 1935PhRv...48...73E. doi : 10.1103/PhysRev.48.73 .
14. Nacido (1909), pág. 25
15. Sommerfeld (1910), págs.670-671
16. von Laue, M. (1921). Die Relativitätstheorie, Band 1 (cuarta edición de "Das Relativitätsprinzip" ed.). Vereg.; Primera edición 1911, segunda edición ampliada 1913, tercera edición ampliada 1919.
17. Einstein (1912), págs. 358-359
18. Lorentz (1913), págs. 34-38; 50-52
19. Kottler (1912), págs.1715; Kottler (1914a), Tabla I; págs. 747–748; Kottler (1914b), págs. 488–489, 503; Kottler (1916), págs. 958–959; (1918), págs. 453–454;
20. Bollert (1922a), pág. 261, 266
21. Lemaitre (1921), págs.166, 168
22. Einstein y Rosen (1935, pág. 74
23. Møller (1952), págs. 121-123; 255-258
24. Nacido (1909), pág. 35
25. Sommerfeld (1910), pág. 672
26. Kottler (1914), págs.489-490
27. Bollert (192 2b ), págs.194-196
28. Mohorovičić (1922), pág. 92, sin exponente debido a un error de imprenta, que fue corregido por Bollert (1922b), p.189, así como por Mohorovičić (1923), p. 54 ${\displaystyle x_{1}}$
29. Bollert (1922b), pág. 189
30. Einstein (1907), §§ 18-21
31. Herglotz, Gustav (1910) [1909], "Über den vom Standpunkt des Relativitätsprinzips aus als starr zu bezeichnenden Körper" [traducción de Wikisource: Sobre cuerpos que deben designarse como "rígidos" desde el punto de vista del principio de relatividad], Annalen der Physik , 336 (2): 393–415, Bibcode :1910AnP...336..393H, doi :10.1002/andp.19103360208
32. von Laue (1911), pág. 109
33. Kottler (1912), págs.1715
34. Kottler (1914a), Tabla I; págs. 747-748
35. Kottler (1914b), págs. 488-489, 503
36. Kottler (1916), págs. 958-959; (1918), págs. 453-454
37. Pauli (1921), págs.647-648

Otras lecturas

Antecedentes útiles:

• Bootby, William M. (1986). Introducción a las variedades diferenciables y la geometría de Riemann . Nueva York: Academic Press. ISBN 0-12-116052-1. Consulte el Capítulo 4 para conocer los antecedentes relacionados con los campos vectoriales en variedades suaves.
• Frankel, Theodore (1979). Curvatura gravitacional: una introducción a la teoría de Einstein . San Francisco: WH Freeman. ISBN 0-7167-1062-5. Consulte el Capítulo 8 para obtener una derivación de la métrica de Fermat.

Coordenadas de Rindler:

• Rindler, Wolfgang (1969). Relatividad esencial . Nueva York, Van Nostrand Reinhold Co. doi :10.1007/978-1-4757-1135-6. ISBN 978-0-387-90201-2.

• Misner, Charles; Thorne, Kip S. y Wheeler, John Archibald (1973). Gravitación . San Francisco: WH Freeman. ISBN 0-7167-0344-0.Consulte la Sección 6.6 .
• Rindler, Wolfgang (2001). Relatividad: Especial, General y Cosmológica . Oxford: Prensa de la Universidad de Oxford. ISBN 0-19-850836-0.
• Ni, Wei-Tou; Zimmermann, Marcos (1978). "Efectos inerciales y gravitacionales en el marco de referencia adecuado de un observador en rotación acelerado". Revisión física D. 17 (6): 1473–1476. Código bibliográfico : 1978PhRvD..17.1473N. doi : 10.1103/PhysRevD.17.1473.

Horizonte de Rindler:

• Jacobson, Ted y Parenti, Renaud (2003). "Entropía del horizonte". Encontró. Física . 33 (2): 323–348. arXiv : gr-qc/0302099 . Código bibliográfico : 2003FoPh...33..323J. doi :10.1023/A:1023785123428. S2CID  16826867.versión impresa
• Barceló, Carlos; Liberati, Stefano y Visser, Matt (2005). "Gravedad analógica". Reseñas vivas en relatividad . 8 (1): 12. arXiv : gr-qc/0505065 . Código Bib : 2005LRR.....8...12B. doi :10.12942/lrr-2005-12. PMC  5255570 . PMID  28179871.