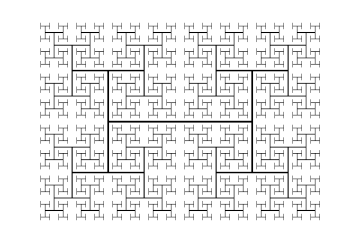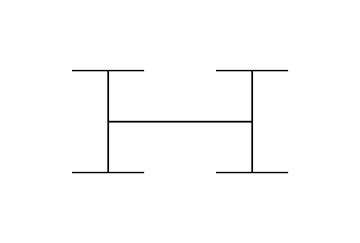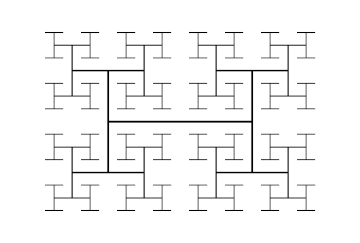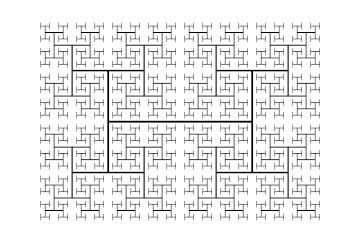
En geometría fractal , el árbol H es una estructura de árbol fractal construida a partir de segmentos de línea perpendiculares , cada uno más pequeño por un factor de la raíz cuadrada de 2 del segmento adyacente más grande. Se llama así porque su patrón repetitivo se parece a la letra "H". Tiene dimensión de Hausdorff 2 y se acerca arbitrariamente a cada punto de un rectángulo . Sus aplicaciones incluyen el diseño VLSI y la ingeniería de microondas.
Un árbol H se puede construir comenzando con un segmento de línea de longitud arbitraria, dibujando dos segmentos más cortos en ángulo recto con el primero a través de sus puntos finales, y continuando en la misma línea, reduciendo (dividiendo) la longitud de los segmentos de línea dibujados en cada etapa por . [1] También se podría definir una variante de esta construcción en la que la longitud en cada iteración se multiplica por una razón menor que , pero para esta variante la forma resultante cubre solo parte de su rectángulo delimitador, con un límite fractal. [2]
Un proceso alternativo que genera el mismo conjunto fractal consiste en comenzar con un rectángulo cuyos lados tengan la proporción , y dividirlo repetidamente en dos rectángulos plateados más pequeños , conectando en cada etapa los dos centroides de los dos rectángulos más pequeños mediante un segmento de línea. Se puede realizar un proceso similar con rectángulos de cualquier otra forma, pero el rectángulo hace que el tamaño del segmento de línea disminuya de manera uniforme en un factor en cada paso, mientras que para otros rectángulos la longitud disminuirá en diferentes factores en los niveles pares e impares de la construcción recursiva.
El árbol H es un fractal autosimilar ; su dimensión de Hausdorff es igual a 2. [2]
Los puntos del árbol H se acercan arbitrariamente a cada punto de un rectángulo (al igual que el rectángulo inicial en la construcción por centroides de rectángulos subdivididos). Sin embargo, no incluye todos los puntos del rectángulo; por ejemplo, no se incluyen los puntos de la bisectriz perpendicular del segmento de línea inicial (excepto el punto medio de este segmento).
En el diseño VLSI , el árbol H puede utilizarse como diseño para un árbol binario completo utilizando un área total que es proporcional al número de nodos del árbol. [3] Además, el árbol H forma un diseño eficiente en cuanto al espacio para árboles en el dibujo de gráficos , [4] y como parte de una construcción de un conjunto de puntos para el cual la suma de las longitudes de los bordes al cuadrado del recorrido del viajante de comercio es grande. [5] Se utiliza comúnmente como una red de distribución de reloj para enrutar señales de temporización a todas las partes de un chip con retrasos de propagación iguales a cada parte, [6] y también se ha utilizado como una red de interconexión para multiprocesadores VLSI. [7]

El árbol H planar se puede generalizar a la estructura tridimensional mediante la adición de segmentos de línea en la dirección perpendicular al plano del árbol H. [8] El árbol H tridimensional resultante tiene una dimensión de Hausdorff igual a 3. Se ha descubierto que el árbol H planar y su versión tridimensional constituyen átomos electromagnéticos artificiales en cristales fotónicos y metamateriales y podrían tener aplicaciones potenciales en la ingeniería de microondas. [8]

El árbol H es un ejemplo de un dosel fractal , en el que el ángulo entre segmentos de línea vecinos es siempre de 180 grados. En su propiedad de acercarse arbitrariamente a cada punto de su rectángulo delimitador, también se asemeja a una curva que llena el espacio , aunque no es en sí una curva.
Topológicamente , un árbol H tiene propiedades similares a las de un dendroid . Sin embargo, no son dendroides: los dendroides deben ser conjuntos cerrados , y los árboles H no son cerrados (su clausura es el rectángulo completo).
Benoit Mandelbrot definió variaciones de la misma estructura de árbol con ramas poligonales engrosadas en lugar de los segmentos de línea del árbol H , y a veces se las llama árbol de Mandelbrot. En estas variaciones, para evitar superposiciones entre las hojas del árbol y sus ramas engrosadas, el factor de escala por el cual se reduce el tamaño en cada nivel debe ser ligeramente mayor que . [9]