Subgrupo parabólico de un grupo de reflexión

En la teoría matemática de los grupos de reflexión , los subgrupos parabólicos son un tipo especial de subgrupo . La definición precisa de qué subgrupos son parabólicos depende del contexto (por ejemplo, si se trata de grupos de Coxeter generales o de grupos de reflexión complejos ), pero en todos los casos la colección de subgrupos parabólicos exhibe importantes buenos comportamientos. Por ejemplo, los subgrupos parabólicos de un grupo de reflexión tienen un conjunto de indexación natural y forman una red cuando se ordenan por inclusión. Las diferentes definiciones de subgrupos parabólicos coinciden esencialmente en el caso de grupos de reflexión reales finitos. Los subgrupos parabólicos surgen en la teoría de grupos algebraicos , a través de su conexión con los grupos de Weyl .

Antecedentes: grupos de reflexión

En un espacio euclidiano (como el plano euclidiano , el espacio tridimensional ordinario o análogos de dimensiones superiores), una reflexión es una simetría del espacio a través de un espejo (técnicamente, a través de un subespacio de dimensión uno más pequeño que todo el espacio) que fija los vectores que se encuentran en el espejo y envía los vectores ortogonales al espejo a sus negativos. Un grupo de reflexión real finito W es un grupo finito generado por reflexiones (es decir, cada transformación lineal en W es una composición de algunas de las reflexiones en W ). ^[1] Por ejemplo, las simetrías de un polígono regular en el plano forman un grupo de reflexión (llamado grupo diedro ), porque cada simetría de rotación del polígono es una composición de dos reflexiones. ^[2] Los grupos de reflexión reales finitos se pueden generalizar de varias maneras, ^[3] y la definición de subgrupo parabólico depende de la elección de la definición.

Cada grupo de reflexión real finito W tiene la estructura de un grupo de Coxeter : ^[1] esto significa que W contiene un subconjunto S de reflexiones (llamadas reflexiones simples ) tales que S genera W , sujeto a relaciones de la forma donde 1 denota la identidad en W y son números que satisfacen para y para . ^{[a] [4]} Por lo tanto, los grupos de Coxeter forman una generalización de los grupos de reflexión reales finitos. $${\displaystyle W=\langle S\mid (ss')^{m_{s,s'}}=1\rangle ,}$$ ${\displaystyle m_{s,s'}}$ ${\displaystyle m_{s,s}=1}$ ${\displaystyle s\in S}$ ${\displaystyle m_{s,s'}\in \{2,3,\ldots \}}$ ${\displaystyle s\neq s'\in S}$

Una generalización separada es considerar la acción geométrica sobre espacios vectoriales cuyo campo subyacente no son los números reales . ^[1] Especialmente, si uno reemplaza los números reales con los números complejos , con una generalización correspondiente de la noción de reflexión, se llega a la definición de un grupo de reflexión complejo . ^[b] Cada grupo de reflexión real puede ser complejizado para dar un grupo de reflexión complejo, por lo que los grupos de reflexión complejos forman otra generalización de grupos de reflexión reales finitos. ^{[6] [7]}

En los grupos de Coxeter

La red de subgrupos parabólicos estándar del grupo simétrico S ₄ , generada como un grupo de Coxeter por las reflexiones simples s ₁ = (1 2) , s ₂ = (2 3) y s ₃ = (3 4) (las transposiciones adyacentes ), con elemento identidad ι

Supóngase que W es un grupo de Coxeter con un conjunto finito S de reflexiones simples. Para cada subconjunto I de S , sea el subgrupo de W generado por . Dichos subgrupos se denominan subgrupos parabólicos estándar de W . ^{[8] [9]} En los casos extremos, es el subgrupo trivial (que contiene solo el elemento identidad de W ) y . ^[10] ${\displaystyle W_{I}}$ ${\displaystyle I}$ ${\displaystyle W_{\varnothing }}$ ${\displaystyle W_{S}=W}$

El par es nuevamente un grupo de Coxeter. Además, la estructura del grupo de Coxeter en es compatible con la de W , en el siguiente sentido: si denota la función de longitud en W con respecto a S (de modo que si el elemento w de W puede escribirse como un producto de k elementos de S y no menos), entonces para cada elemento w de , se tiene que . Es decir, la longitud de w es la misma ya sea que se considere como un elemento de W o de . ^{[8] [9]} Lo mismo es cierto para el orden de Bruhat : si u y w son elementos de , entonces en el orden de Bruhat en si y solo si en el orden de Bruhat en W . ^[11] ${\displaystyle (W_{I},I)}$ ${\displaystyle W_{I}}$ ${\displaystyle \ell _{S}}$ ${\displaystyle \ell _{S}(w)=k}$ ${\displaystyle W_{I}}$ ${\displaystyle \ell _{S}(w)=\ell _{I}(w)}$ ${\displaystyle W_{I}}$ ${\displaystyle W_{I}}$ ${\displaystyle u\leq w}$ ${\displaystyle W_{I}}$ ${\displaystyle u\leq w}$

Si I y J son dos subconjuntos de S , entonces si y solo si , , y el grupo más pequeño que contiene tanto a como es . En consecuencia, la red de subgrupos parabólicos estándar de W es una red booleana . ^{[8] [9]} ${\displaystyle W_{I}=W_{J}}$ ${\displaystyle I=J}$ ${\displaystyle W_{I}\cap W_{J}=W_{I\cap J}}$ ${\displaystyle \langle W_{I},W_{J}\rangle }$ ${\displaystyle W_{I}}$ ${\displaystyle W_{J}}$ ${\displaystyle W_{I\cup J}}$

Dado un subgrupo parabólico estándar de un grupo de Coxeter W , las clases laterales de en W tienen un sistema particularmente bueno de representantes: sea el conjunto de elementos en W que no tienen ningún elemento de I como descendencia derecha. ^[c] Entonces para cada , hay elementos únicos y tales que . Además, este es un producto aditivo de longitud, es decir, . Además, u es el elemento de longitud mínima en la clase lateral . ^{[8] [13]} Una construcción análoga es válida para clases laterales derechas. ^[14] La colección de todas las clases laterales izquierdas de subgrupos parabólicos estándar es una construcción posible del complejo de Coxeter . ^[15] ${\displaystyle W_{I}}$ ${\displaystyle W_{I}}$ ${\displaystyle W^{I}}$ $${\displaystyle W^{I}=\{w\in W\colon \ell _{S}(ws)>\ell _{S}(w){\text{ for all }}s\in I\}}$$ ${\displaystyle w\in W}$ ${\displaystyle u\in W^{I}}$ ${\displaystyle v\in W_{I}}$ ${\displaystyle w=uv}$ ${\displaystyle \ell _{S}(w)=\ell _{S}(u)+\ell _{S}(v)}$ ${\displaystyle wW_{I}}$

En términos del diagrama de Coxeter-Dynkin , los subgrupos parabólicos estándar surgen tomando un subconjunto de los nodos del diagrama y las aristas inducidas entre esos nodos, borrando todos los demás. ^[16] Los únicos subgrupos parabólicos normales surgen tomando una unión de componentes conectados del diagrama, y ​​todo el grupo W es el producto directo de los grupos de Coxeter irreducibles que corresponden a los componentes. ^[17]

En grupos de reflexión complejos

La red de subgrupos parabólicos del grupo diedro D _2×4 , representada como un grupo de reflexión real, está formada por el subgrupo trivial, los cuatro subgrupos de dos elementos generados por una única reflexión y el grupo entero. Ordenados por inclusión, dan la misma red que la red de espacios fijos ordenados por inclusión inversa.

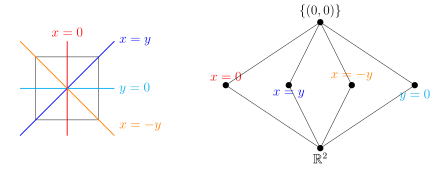
Supóngase que W es un grupo de reflexión complejo que actúa sobre un espacio vectorial complejo V . Para cualquier subconjunto , sea el subconjunto de W que consiste en aquellos elementos en W que fijan cada elemento de A . ^[d] Tal subgrupo se denomina subgrupo parabólico de W . ^[19] En los casos extremos, y es el subgrupo trivial de W que contiene solo el elemento identidad. ${\displaystyle A\subseteq V}$ $${\displaystyle W_{A}=\{w\in W\colon w(a)=a{\text{ for all }}a\in A\}}$$ ${\displaystyle W_{\varnothing }=W_{\{0\}}=W}$ ${\displaystyle W_{V}}$

De un teorema de Steinberg (1964) se sigue que cada subgrupo parabólico de un grupo de reflexión complejo W es un grupo de reflexión, generado por las reflexiones en W que fijan cada punto en A . ^[20] Puesto que W actúa linealmente sobre V , donde es el espacio de A (es decir, el subespacio lineal más pequeño de V que contiene a A ). ^[19] De hecho, hay una elección simple de subespacios A que indexan los subgrupos parabólicos: cada reflexión en W fija un hiperplano (es decir, un subespacio de V cuya dimensión es 1 menor que la de V ) puntualmente, y la colección de todos estos hiperplanos es la disposición de reflexión de W . ^[21] La colección de todas las intersecciones de subconjuntos de estos hiperplanos, ^[e] parcialmente ordenados por inclusión, es una red . ^[22] Los elementos de la red son precisamente los espacios fijos de los elementos de W (es decir, para cada intersección I de hiperplanos reflectores, hay un elemento tal que ). ^{[23] [24]} El mapa que envía es una biyección de orden inverso entre subespacios en y subgrupos parabólicos de W . ^[24] ${\displaystyle W_{A}}$ ${\displaystyle W_{A}=W_{\overline {A}}}$ ${\displaystyle {\overline {A}}}$ ${\displaystyle L_{W}}$ ${\displaystyle w\in W}$ ${\displaystyle \{v\in V\colon w(v)=v\}=I}$ ${\displaystyle I\mapsto W_{I}}$ ${\displaystyle I\in L_{W}}$ ${\displaystyle L_{W}}$

Concordancia de definiciones en grupos de reflexión reales finitos

Sea W un grupo de reflexión real finito; es decir, W es un grupo finito de transformaciones lineales en un espacio euclidiano real de dimensión finita que se genera mediante reflexiones ortogonales. Como se mencionó anteriormente (ver § Antecedentes: grupos de reflexión), W puede verse como un grupo de Coxeter y como un grupo de reflexión complejo. Para un grupo de reflexión real W , los subgrupos parabólicos de W (vistos como un grupo de reflexión complejo) no son todos subgrupos parabólicos estándar de W (cuando se los ve como un grupo de Coxeter, después de especificar un conjunto generador de Coxeter fijo S ), ya que hay muchos más subespacios en la red de intersección de su disposición de reflexión que subconjuntos de S . Sin embargo, en un grupo de reflexión real finito W , cada subgrupo parabólico es conjugado a un subgrupo parabólico estándar con respecto a S . ^[25]

Ejemplos

La red de subgrupos parabólicos del grupo S^B4
_​, representadas como permutaciones con signo de {−2, −1, 1, 2}, con identidad ι

El grupo simétrico , que consiste en todas las permutaciones de , es un grupo de Coxeter con respecto al conjunto de transposiciones adyacentes , ..., . Los subgrupos parabólicos estándar de (que también se conocen como subgrupos de Young ) son los subgrupos de la forma , donde son números enteros positivos con suma n , en los que el primer factor en el producto directo permuta los elementos entre sí, el segundo factor permuta los elementos entre sí, y así sucesivamente. ^{[26] [14]} ${\displaystyle S_{n}}$ ${\displaystyle \{1,\ldots ,n\}}$ ${\displaystyle (1\ 2)}$ ${\displaystyle (n-1\ n)}$ ${\displaystyle S_{n}}$ ${\displaystyle S_{a_{1}}\times \cdots \times S_{a_{k}}}$ ${\displaystyle a_{1},\ldots ,a_{k}}$ ${\displaystyle \{1,\ldots ,a_{1}\}}$ ${\displaystyle \{a_{1}+1,\ldots ,a_{1}+a_{2}\}}$

El grupo hiperoctaédrico , que consiste en todas las permutaciones con signo de (es decir, las biyecciones w en ese conjunto tales que para todo i ), tiene como subgrupos parabólicos estándar máximos los estabilizadores de para . ^[27] ${\displaystyle S_{n}^{B}}$ ${\displaystyle \{\pm 1,\ldots ,\pm n\}}$ ${\displaystyle w(-i)=-w(i)}$ ${\displaystyle \{i+1,\ldots ,n\}}$ ${\displaystyle i\in \{1,\ldots ,n\}}$

Definiciones más generales en la teoría de Coxeter

En un grupo de Coxeter generado por un conjunto finito S de reflexiones simples, se puede definir un subgrupo parabólico como cualquier conjugado de un subgrupo parabólico estándar. Según esta definición, sigue siendo cierto que la intersección de dos subgrupos parabólicos cualesquiera es un subgrupo parabólico. Lo mismo no se aplica en general a los grupos de Coxeter de rango infinito. ^[28]

Si W es un grupo y T es un subconjunto de W , el par se denomina sistema dual de Coxeter si existe un subconjunto S de T tal que es un sistema de Coxeter y de modo que T es el conjunto de todas las reflexiones (conjugadas de las reflexiones simples) en W . Para un sistema dual de Coxeter , se dice que un subgrupo de W es un subgrupo parabólico si es un parabólico estándar (como en § En los grupos de Coxeter) de para alguna elección de reflexiones simples S para . ^{[29] [f]} ${\displaystyle (W,T)}$ ${\displaystyle (W,S)}$ $${\displaystyle T=\{wsw^{-1}\colon w\in W,s\in S\},}$$ ${\displaystyle (W,T)}$ ${\displaystyle (W,S)}$ ${\displaystyle (W,T)}$

En algunos sistemas duales de Coxeter, todos los conjuntos de reflexiones simples son conjugados entre sí; en este caso, los subgrupos parabólicos con respecto a un sistema simple (es decir, los conjugados de los subgrupos parabólicos estándar) coinciden con los subgrupos parabólicos con respecto a cualquier otro sistema simple. Sin embargo, incluso en ejemplos finitos, esto puede no ser así: por ejemplo, si W es el grupo diedro con 10 elementos, vistos como simetrías de un pentágono regular , y T es el conjunto de simetrías de reflexión del polígono, entonces cualquier par de reflexiones en T forma un sistema simple para , pero no todos los pares de reflexiones son conjugados entre sí. ^[29] Sin embargo, si W es finito, entonces los subgrupos parabólicos (en el sentido anterior) coinciden con los subgrupos parabólicos en el sentido clásico (es decir, los conjugados de los subgrupos parabólicos estándar con respecto a una única elección fija de reflexiones simples S ). ^[31] El mismo resultado no se cumple en general para grupos de Coxeter infinitos. ^[32] ${\displaystyle (W,T)}$

Grupos de Coxeter afines y cristalográficos

Cuando W es un grupo de Coxeter afín , el grupo de Weyl finito asociado es siempre un subgrupo parabólico maximalista, cuyo diagrama de Coxeter-Dynkin es el resultado de eliminar un nodo del diagrama de W. En particular, las funciones de longitud en los grupos finitos y afines coinciden. ^[33] De hecho, cada subgrupo parabólico estándar de un grupo de Coxeter afín es finito. ^[34] Como en el caso de los grupos de reflexión reales finitos, cuando consideramos la acción de un grupo de Coxeter afín W en un espacio euclidiano V , los conjugados de los subgrupos parabólicos estándar de W son precisamente los subgrupos de la forma para algún subconjunto A de V. ^[35 ] $${\displaystyle \{w\in W\colon w(a)=a{\text{ for all }}a\in A\}}$$

Si W es un grupo de Coxeter cristalográfico, ^[g] entonces cada subgrupo parabólico de W también es cristalográfico. ^[36]

Conexión con la teoría de grupos algebraicos

Si G es un grupo algebraico y B es un subgrupo de Borel para G , entonces un subgrupo parabólico de G es cualquier subgrupo que contenga a B . ^[h] Si además G tiene un par ( B , N ) , entonces el grupo cociente asociado es un grupo de Coxeter, llamado grupo de Weyl de G . Entonces el grupo G tiene una descomposición de Bruhat en clases laterales dobles (donde es la unión disjunta ), y los subgrupos parabólicos de G que contienen a B son precisamente los subgrupos de la forma donde es un subgrupo parabólico estándar de W . ^[39] ${\displaystyle W=B/(B\cap N)}$ ${\displaystyle G=\bigsqcup _{w\in W}BwB}$ ${\displaystyle \sqcup }$ $${\displaystyle P_{J}=BW_{J}B}$$ ${\displaystyle W_{J}}$

Cierres parabólicos

Supóngase que W es un grupo de Coxeter de rango finito (es decir, el conjunto S de generadores simples es finito). Dado cualquier subconjunto X de W , se puede definir el cierre parabólico de X como la intersección de todos los subgrupos parabólicos que contienen a X . Como se mencionó anteriormente, en este caso la intersección de dos subgrupos parabólicos cualesquiera de W es nuevamente un subgrupo parabólico de W , y en consecuencia el cierre parabólico de X es un subgrupo parabólico de W ; en particular, es el subgrupo parabólico mínimo (único) de W que contiene a X . ^[28] El mismo análisis se aplica a los grupos de reflexión complejos, donde el cierre parabólico de X es también el estabilizador puntual del espacio de puntos fijos de X . ^[40] Lo mismo no se aplica a los grupos de Coxeter de rango infinito. ^[28]

Grupos de trenzas

Cada grupo de Coxeter está asociado a otro grupo llamado grupo Artin-Tits o grupo trenzado generalizado , que se define omitiendo las relaciones para cada generador de su presentación de Coxeter. ^{[i] [41]} Aunque los grupos trenzados generalizados no son grupos de reflexión, heredan una noción de subgrupos parabólicos: un subgrupo parabólico estándar de un grupo trenzado generalizado es un subgrupo generado por un subconjunto del conjunto generador estándar S , y un subgrupo parabólico es cualquier subgrupo conjugado a un parabólico estándar. ^[42] ${\displaystyle s^{2}=1}$ ${\displaystyle s\in S}$

Se dice que un grupo trenzado generalizado es de tipo esférico si el grupo de Coxeter asociado es finito. Si B es un grupo trenzado generalizado de tipo esférico, entonces la intersección de dos subgrupos parabólicos cualesquiera de B es también un subgrupo parabólico. En consecuencia, los subgrupos parabólicos de B forman una red bajo inclusión. ^[42]

Para un grupo de reflexión real finito W , el grupo trenzado generalizado asociado puede definirse en lenguaje puramente topológico , sin hacer referencia a una presentación de grupo particular. ^[j] Esta definición se extiende naturalmente a grupos de reflexión complejos finitos. ^[43] Los subgrupos parabólicos también pueden definirse en este contexto. ^[44]

Notas al pie

1. En los grupos de Coxeter generales, también se permite la posibilidad de que no exista relación entre s y s ' —pero esta situación no puede darse en un grupo finito. ${\displaystyle m_{s,s'}=\infty }$
2. En algunas fuentes, estos grupos también se conocen como grupos de reflexión unitaria o grupos de pseudorreflexión complejos . De manera similar, a veces las reflexiones complejas (transformaciones lineales que fijan un hiperplano puntualmente) se denominan pseudorreflexiones . ^[5]
3. Un descenso recto de un elemento w en un grupo de Coxeter es una reflexión simple s tal que . ^[12] ${\displaystyle \ell _{S}(ws)>\ell _{S}(w)}$
4. A veces estos subgrupos se denominan grupos de isotropía . ^[18]
5. Incluyendo todo el espacio V , como la intersección vacía.
6. En el caso de un grupo de reflexión real finito, esta definición difiere de la clásica, donde S proviene necesariamente de las reflexiones cuyos hiperplanos reflectores forman los límites de una cámara. ^[30]
7. Es decir, si W es un grupo de Coxeter (posiblemente infinito) que estabiliza una red en su representación geométrica natural.
8. Este uso de la frase "subgrupo parabólico" fue introducido por Roger Godement en su artículo Godement (1961). ^{[37] [38]}
9. El nombre "grupo trenzado generalizado" surge del hecho de que, en el caso especial del grupo simétrico, el grupo Artin-Tits asociado es el grupo trenzado en n hebras. ${\displaystyle W=S_{n}}$
10. En particular, el grupo W actúa sobre el complemento de la complejización de la disposición de sus hiperplanos reflectores; el grupo trenzado generalizado de W es el grupo fundamental del cociente de este espacio bajo la acción de W .

1. Kane (2001), pág. 1.
2. Kane (2001), págs. 8-14.
3. Humphreys (1990), págs. xi–xii.
4. Humphreys (1990), §1.9.
5. Kane (2001), pág. 160.
6. Lehrer y Taylor (2009), pág. 1.
7. Humphreys (1990), pág. 66.
8. Björner y Brenti (2005), §2.4.
9. Humphreys (1990), §5.5.
10. Humphreys (1990), §1.10.
11. Humphreys (1990), §5.10.
12. Björner y Brenti (2005), pág. 17.
13. Humphreys (1990), §5.12.
14. Björner y Brenti (2005), pág. 41.
15. Björner y Brenti (2005), págs. 86–7.
16. Björner y Brenti (2005), pág. 39.
17. Humphreys (1990), págs. 118, 129.
18. Kane (2001), pág. 60.
19. Lehrer y Taylor (2009), pág. 171.
20. Lehrer y Taylor (2009), §9.7.
21. Orlik y Terao (1992), pág. 215.
22. Orlik y Terao (1992), §2.1.
23. Lehrer y Taylor (2009), §9.3.
24. Broué (2010), §4.2.4.
25. Kane (2001), §5.2.
26. Kane (2001), pág. 58.
27. Björner y Brenti (2005), pág. 248.
28. Nuida (2012).
29. Baumeister et al. (2014).
30. Reiner, Ripoll & Stump (2017), Ejemplo 1.2.
31. Baumeister et al. (2017), Proposición 1.4 y Corolario 4.4.
32. Gobet (2017), Ejemplo 2.2.
33. Humphreys (1990), pág. 114.
34. Humphreys (1990), pág. 96.
35. Kane (2001), pág. 130.
36. Humphreys (1990), pág. 136.
37. Borel (2001), capítulo VI, sección 2.
38. Chow (2010).
39. Digne y Michel (1991), págs. 19-21.
40. Taylor (2012).
41. McCammond y Sulway (2017).
42. Cumplido et al. (2019).
43. Broué (2010), §4.2.5.
44. González-Meneses & Marín (2022).

Referencias

• Baumeister, Barbara; Dyer, Matthew; Stump, Christian; Wegener, Patrick (2014), "Una nota sobre la acción transitiva de Hurwitz en descomposiciones de elementos parabólicos de Coxeter", Actas de la American Mathematical Society , Serie B, 1 (13): 149–154, arXiv : 1402.2500 , doi : 10.1090/S2330-1511-2014-00017-1
• Baumeister, Barbara; Gobet, Thomas; Roberts, Kieran; Wegener, Patrick (2017), "Sobre la acción de Hurwitz en grupos finitos de Coxeter", Journal of Group Theory , 20 (1): 103–131, arXiv : 1512.04764 , doi :10.1515/jgth-2016-0025, S2CID  44035800
• Björner, Anders ; Brenti, Francesco (2005), Combinatoria de grupos Coxeter , Springer, doi :10.1007/3-540-27596-7, ISBN 978-3540-442387, Identificador único  115235335
• Borel, Armand (2001), Ensayos sobre la historia de los grupos de Lie y los grupos algebraicos , History of Mathematics, vol. 21, American Mathematical Society y London Mathematical Society, ISBN 0-8218-0288-7
• Broué, Michel (2010), Introducción a los grupos de reflexión complejos y sus grupos trenzados , Lecture Notes in Mathematics , vol. 1988, Springer-Verlag, doi :10.1007/978-3-642-11175-4, ISBN 978-3-642-11174-7
• Chow, Timothy (2010), "¿Por qué los subgrupos parabólicos se denominan "subgrupos parabólicos"?", MathOverflow , et al. , consultado el 16 de febrero de 2024
• Cumplido, María; Gebhardt, Volker; González-Meneses, Juan; Wiest, Bert (2019), "Sobre subgrupos parabólicos de grupos Artin–Tits de tipo esférico", Advances in Mathematics , 352 : 572–610, arXiv : 1712.06727 , doi : 10.1016/j.aim.2019.06.010
• Digne, François; Michel, Jean (1991), Representaciones de grupos finitos de tipo Lie , London Mathematical Society Student Texts, vol. 21, Cambridge University Press, ISBN 0-521-40117-8
• Gobet, Thomas (2017), "Sobre las descomposiciones de ciclos en grupos de Coxeter", Séminaire Lotharingien de Combinatoire , 78B : art. 45, arXiv : 1611.03442
• Godement, Roger (1961), "Groupes linéaires algébriques sur un corps parfait", Séminaire Bourbaki , 13
• González-Meneses, Juan; Marin, Ivan (2022), Subgrupos parabólicos de grupos trenzados complejos I , arXiv : 2208.11938v1
• Humphreys, James E. (1990), Grupos de reflexión y grupos de Coxeter , Cambridge University Press, doi :10.1017/CBO9780511623646, ISBN 0-521-37510-X, Número de identificación del sujeto  121077209
• Kane, Richard (2001), Grupos de reflexión y teoría invariante , CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, Springer-Verlag, doi :10.1007/978-1-4757-3542-0, ISBN 0-387-98979-X, Número de identificación del sujeto  119694827
• Lehrer, Gustav I.; Taylor, Donald E. (2009), Grupos de reflexión unitaria , Serie de conferencias de la Sociedad Matemática Australiana, vol. 20, Cambridge University Press , ISBN 978-0-521-74989-3
• McCammond, Jon; Sulway, Robert (2017), "Grupos de Artin de tipo euclidiano", Inventiones Mathematicae , 210 (1): 231–282, arXiv : 1312.7770 , Bibcode :2017InMat.210..231M, doi :10.1007/s00222-017-0728-2, S2CID  253738806
• Nuida, Koji (2012), "Subgrupos localmente parabólicos en grupos de Coxeter de rangos arbitrarios", Journal of Algebra , 350 : 207–217, arXiv : 1006.4709 , doi :10.1016/j.jalgebra.2011.11.005
• Orlik, Peter ; Terao, Hiroaki (1992), Disposiciones de hiperplanos , Grundlehren der mathematischen Wissenschaften, Springer, doi :10.1007/978-3-662-02772-1, ISBN 978-3-540-55259-8
• Reiner, Víctor; Ripoll, Vivien; Stump, Christian (2017), "Sobre elementos de Coxeter no conjugados en grupos de reflexión bien generados", Mathematische Zeitschrift , 285 (3–4): 1041–1062, arXiv : 1404.5522 , doi :10.1007/s00209-016-1736- 4, S2CID  253752187
• Steinberg, Robert (1964), "Ecuaciones diferenciales invariantes bajo grupos de reflexión finitos", Transactions of the American Mathematical Society , 112 (3): 392–400, doi :10.1090/S0002-9947-1964-0167535-3
• Taylor, DE (2012), "Subgrupos de reflexión de grupos de reflexión complejos finitos", Journal of Algebra , 366 : 218–234, arXiv : 1201.1348 , doi :10.1016/j.jalgebra.2012.04.033