Junta apolínea

Fractal compuesto de círculos tangentes

Un ejemplo de una junta apolínea

En matemáticas , una junta apolínea o red apolínea es un fractal generado a partir de un triple de círculos, cada uno tangente a los otros dos, y rellenando sucesivamente más círculos, cada uno tangente a otros tres. Recibe su nombre del matemático griego Apolonio de Perga . ^[1]

Construcción

Círculos mutuamente tangentes. Dados tres círculos mutuamente tangentes ( negros ), en general hay otros dos círculos mutuamente tangentes a ellos ( rojos ).

La construcción de la junta apolínea comienza con tres círculos , , y (negros en la figura), que son tangentes entre sí, pero que no tienen un solo punto de triple tangencia. Estos círculos pueden ser de diferentes tamaños entre sí, y se permite que dos estén dentro del tercero, o que los tres estén uno fuera del otro. Como descubrió Apolonio, existen dos círculos más y (rojos) que son tangentes a los tres círculos originales; estos se llaman círculos apolíneos . Estos cinco círculos están separados entre sí por seis regiones triangulares curvas, cada una limitada por los arcos de tres círculos tangentes por pares. La construcción continúa agregando seis círculos más, uno en cada uno de estos seis triángulos curvos, tangentes a sus tres lados. Estos a su vez crean 18 triángulos curvos más, y la construcción continúa llenándolos nuevamente con círculos tangentes, ad infinitum. ${\displaystyle C_{1}}$ ${\displaystyle C_{2}}$ ${\displaystyle C_{3}}$ ${\displaystyle C_{4}}$ ${\displaystyle C_{5}}$

Continuando de esta manera etapa por etapa, la construcción agrega nuevos círculos en la etapa , dando un total de círculos después de las etapas. En el límite, este conjunto de círculos es una junta apolínea. En ella, cada par de círculos tangentes tiene una cadena de Pappus infinita de círculos tangentes a ambos círculos del par. ${\displaystyle 2\cdot 3^{n}}$ ${\displaystyle n}$ ${\displaystyle 3^{n+1}+2}$ ${\displaystyle n}$

En el caso límite (0,0,1,1), los dos círculos más grandes se reemplazan por líneas rectas paralelas. Esto produce una familia de círculos de Ford .

El tamaño de cada nuevo círculo está determinado por el teorema de Descartes , que establece que, para cualesquiera cuatro círculos mutuamente tangentes, los radios de los círculos obedecen a la ecuación Esta ecuación puede tener una solución con un radio negativo; esto significa que uno de los círculos (el de radio negativo) rodea a los otros tres. Uno o dos de los círculos iniciales de esta construcción, o los círculos resultantes de esta construcción, pueden degenerar en una línea recta, que puede pensarse como un círculo con radio infinito. Cuando hay dos líneas, deben ser paralelas, y se considera que son tangentes en un punto en el infinito . Cuando la junta incluye dos líneas en el eje y una unidad por encima de él, y un círculo de diámetro unidad tangente a ambas líneas centradas en el eje , entonces los círculos que son tangentes al eje son los círculos de Ford , importantes en la teoría de números . ${\displaystyle r_{i}}$ $${\displaystyle \left({\frac {1}{r_{1}}}+{\frac {1}{r_{2}}}+{\frac {1}{r_{3}}}+{\frac {1}{r_{4}}}\right)^{2}=2\left({\frac {1}{r_{1}^{2}}}+{\frac {1}{r_{2}^{2}}}+{\frac {1}{r_{3}^{2}}}+{\frac {1}{r_{4}^{2}}}\right).}$$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$

La junta apolínea tiene una dimensión de Hausdorff de aproximadamente 1,3057. ^{[2] [3]} Debido a que tiene una dimensión fraccionaria bien definida, aunque no es precisamente autosimilar , se puede considerar como un fractal .

Simetrías

Las transformaciones de Möbius del plano preservan las formas y tangencias de los círculos y, por lo tanto, preservan la estructura de una junta apolínea. Dos triples cualesquiera de círculos mutuamente tangentes en una junta apolínea pueden ser mapeados entre sí por una transformación de Möbius, y dos juntas apolíneas cualesquiera pueden ser mapeadas entre sí por una transformación de Möbius. En particular, para dos círculos tangentes cualesquiera en cualquier junta apolínea, una inversión en un círculo centrado en el punto de tangencia (un caso especial de una transformación de Möbius) transformará estos dos círculos en dos líneas paralelas, y transformará el resto de la junta en la forma especial de una junta entre dos líneas paralelas. Las composiciones de estas inversiones se pueden utilizar para transformar dos puntos de tangencia cualesquiera en uno otro. Las transformaciones de Möbius también son isometrías del plano hiperbólico , por lo que en geometría hiperbólica todas las juntas apolíneas son congruentes. En cierto sentido, sólo hay una única junta apolínea, hasta la isometría (hiperbólica).

La junta apolínea es el conjunto límite de un grupo de transformaciones de Möbius conocido como grupo kleiniano . ^[4]

En general, para las transformaciones de simetría euclidiana en lugar de las transformaciones de Möbius, la junta apolínea heredará las simetrías de su conjunto generador de tres círculos. Sin embargo, algunas ternas de círculos pueden generar juntas apolíneas con mayor simetría que la terna inicial; esto sucede cuando la misma junta tiene un conjunto diferente y más simétrico de círculos generadores. Los casos particularmente simétricos incluyen la junta apolínea entre dos líneas paralelas (con simetría diedral infinita ), la junta apolínea generada por tres círculos congruentes en un triángulo equilátero (con la simetría del triángulo) y la junta apolínea generada por dos círculos de radio 1 rodeados por un círculo de radio 2 (con dos líneas de simetría reflexiva).

Empaquetamientos de círculos apolíneos integrales

• 
  Empaquetamiento circular apolíneo integral definido por curvaturas circulares de (−1, 2, 2, 3)
• 
  Empaquetamiento circular apolíneo integral definido por curvaturas circulares de (−3, 5, 8, 8)
• 
  Empaquetamiento circular apolíneo integral definido por curvaturas circulares de (−12, 25, 25, 28)
• 
  Empaquetamiento circular apolíneo integral definido por curvaturas circulares de (−6, 10, 15, 19)
• 
  Empaquetamiento circular apolíneo integral definido por curvaturas circulares de (−10, 18, 23, 27)

Si cuatro círculos mutuamente tangentes en una junta apolínea tienen todos una curvatura entera (la inversa de su radio), entonces todos los círculos en la junta tendrán una curvatura entera. ^[5] Dado que la ecuación que relaciona las curvaturas en una junta apolínea, integral o no, es se deduce que uno puede moverse de un cuádruple de curvaturas a otro mediante saltos de Vieta , tal como cuando se encuentra un nuevo número de Markov . Las primeras de estas juntas apolíneas integrales se enumeran en la siguiente tabla. La tabla enumera las curvaturas de los círculos más grandes en la junta. Solo se necesitan las primeras tres curvaturas (de las cinco que se muestran en la tabla) para describir completamente cada junta; todas las demás curvaturas se pueden derivar de estas tres. $${\displaystyle a^{2}+b^{2}+c^{2}+d^{2}=2ab+2ac+2ad+2bc+2bd+2cd,\,}$$

Enumeración de empaquetamientos de círculos apolíneos integrales

Las curvaturas son una raíz cuádruple (la más pequeña en algún empaquetamiento de círculos integrales) si . Son primitivas cuando . Definir un nuevo conjunto de variables mediante la ecuación matricial da un sistema donde satisface la ecuación de Descartes precisamente cuando . Además, es primitiva precisamente cuando , y es una raíz cuádruple precisamente cuando . ^[5] ${\displaystyle (a,b,c,d)}$ ${\displaystyle a<0\leq b\leq c\leq d}$ ${\displaystyle \gcd(a,b,c,d)=1}$ ${\displaystyle (x,d_{1},d_{2},m)}$ $${\displaystyle {\begin{bmatrix}a\\b\\c\\d\end{bmatrix}}={\begin{bmatrix}1&0&0&0\\-1&1&0&0\\-1&0&1&0\\-1&1&1&-2\end{bmatrix}}{\begin{bmatrix}x\\d_{1}\\d_{2}\\m\end{bmatrix}}}$$ ${\displaystyle (a,b,c,d)}$ ${\displaystyle x^{2}+m^{2}=d_{1}d_{2}}$ ${\displaystyle (a,b,c,d)}$ ${\displaystyle \gcd(x,d_{1},d_{2})=1}$ ${\displaystyle (a,b,c,d)}$ ${\displaystyle x<0\leq 2m\leq d_{1}\leq d_{2}}$

Esta relación se puede utilizar para encontrar todos los cuádruples de raíz primitivos con una curva negativa dada . De y se deduce que , y por lo tanto que . Por lo tanto, cualquier cuádruple de raíz satisfará . Al iterar sobre todos los valores posibles de , , y se pueden encontrar todos los cuádruples de raíz primitivos. ^[6] El siguiente código Python demuestra este algoritmo, produciendo los cuádruples de raíz primitivos enumerados anteriormente. ${\displaystyle x}$ ${\displaystyle 2m\leq d_{1}}$ ${\displaystyle 2m\leq d_{2}}$ ${\displaystyle 4m^{2}\leq d_{1}d_{2}}$ ${\displaystyle 3m^{2}\leq d_{1}d_{2}-m^{2}=x^{2}}$ ${\displaystyle 0\leq m\leq |x|/{\sqrt {3}}}$ ${\displaystyle m}$ ${\displaystyle d_{1}}$ ${\displaystyle d_{2}}$

importar  matemáticasdef  obtener_curvas_primitivas ( n :  int ) :  si  n  ==  0 :  rendimiento  0 ,  0 ,  1 ,  1  retorno  para  m  en  rango ( math.ceil ( n / math.sqrt ( 3 ) ) ) : s = m ** 2 + n ** 2 para d1 en rango ( max ( 2 * m , 1 ) , math.floor ( math.sqrt ( s ) ) + 1 ) : d2 , resto = divmod ( s , d1 ) si resto == 0 y math.gcd ( n , d1 , d2 ) == 1 : rendimiento - n , d1 + n , d2 + n , d1 + d2 + n - 2 * m​​​                                                 para  n  en  rango ( 15 ):  para  curvas  en  get_primitive_bends ( n ):  print ( curvas )

Las curvaturas que aparecen en un empaquetamiento de círculo apolíneo integral primitivo deben pertenecer a un conjunto de seis u ocho posibles clases de residuos módulo 24, y la evidencia numérica respaldó que cualquier entero suficientemente grande de estas clases de residuos también estaría presente como una curvatura dentro del empaquetamiento. ^[7] Esta conjetura, conocida como conjetura local-global, resultó ser falsa en 2023. ^{[8] [9]}

Simetría de empaquetamientos de círculos apolíneos integrales

Existen múltiples tipos de simetría diedra que pueden ocurrir con una junta dependiendo de la curvatura de los círculos.

Sin simetría

Si ninguna de las curvaturas se repite dentro de las primeras cinco, la junta no contiene simetría, lo que está representado por el grupo de simetría C ₁ ; la junta descrita por las curvaturas (−10, 18, 23, 27) es un ejemplo.

D₁simetría

Siempre que dos de los cinco círculos más grandes de la junta tengan la misma curvatura, dicha junta tendrá simetría D ₁ , que corresponde a una reflexión a lo largo de un diámetro del círculo delimitador, sin simetría rotacional.

D₂simetría

Si se repiten dos curvaturas diferentes dentro de las primeras cinco, la junta tendrá simetría D ₂ ; dicha simetría consiste en dos reflexiones (perpendiculares entre sí) a lo largo de los diámetros del círculo delimitador, con una simetría rotacional doble de 180°. La junta descrita por las curvaturas (−1, 2, 2, 3) es la única junta apolínea (hasta un factor de escala) que posee simetría D ₂ .

D₃simetría

No existen juntas enteras con _simetría D3 .

Si los tres círculos con la curvatura positiva más pequeña tienen la misma curvatura, la junta tendrá simetría D ₃ , que corresponde a tres reflexiones a lo largo de los diámetros del círculo delimitador (espaciados 120° entre sí), junto con una simetría rotacional triple de 120°. En este caso, la relación entre la curvatura del círculo delimitador y los tres círculos internos es 2 √ 3  − 3. Como esta relación no es racional, ningún empaquetamiento de círculo apolíneo integral posee esta simetría D ₃ , aunque muchos empaquetamientos se acercan a ella.

Casi-D₃simetría

(−15, 32, 32, 33)

(−15, 32, 32, 33)

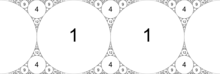
La figura de la izquierda es una junta apolínea integral que parece tener simetría D ₃ . La misma figura se muestra a la derecha, con etiquetas que indican las curvaturas de los círculos interiores, lo que ilustra que la junta en realidad posee solo la simetría D ₁ común a muchas otras juntas apolíneas integrales.

La siguiente tabla enumera más de estas juntas apolíneas casi - D ₃ integrales. La secuencia tiene algunas propiedades interesantes, y la tabla enumera una factorización de las curvaturas, junto con el multiplicador necesario para pasar del conjunto anterior al actual. Los valores absolutos de las curvaturas de los discos "a" obedecen a la relación de recurrencia a ( n ) = 4 a ( n − 1) − a ( n − 2) (secuencia A001353 en la OEIS ), de la que se deduce que el multiplicador converge a √ 3  + 2 ≈ 3,732050807.

Curvas secuenciales

Juntas apolíneas anidadas

Para cualquier entero n  > 0, existe una junta apolínea definida por las siguientes curvaturas:
(− n ,  n  + 1,  n ( n  + 1),  n ​​( n  + 1) + 1).
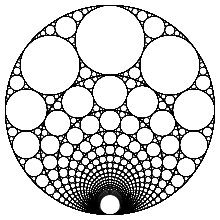
Por ejemplo, las juntas definidas por (−2, 3, 6, 7), (−3, 4, 12, 13), (−8, 9, 72, 73) y (−9, 10, 90, 91) siguen todas este patrón. Debido a que cada círculo interior definido por n  + 1 puede convertirse en el círculo delimitador (definido por − n ) en otra junta, estas juntas pueden estar anidadas . Esto se demuestra en la figura de la derecha, que contiene estas juntas secuenciales con n que va desde 2 hasta 20.

Historia

Aunque la junta apolínea recibe su nombre de Apolonio de Perge (debido a que su construcción depende de la solución del problema de Apolonio ), la descripción más antigua de la junta es de 1706 por Leibniz en una carta a Des Bosses . ^[10] La primera definición moderna de la junta apolínea la dan Kasner y Supnick. ^[11]

Véase también

Empaquetamiento de esferas apolíneas

• Red apolínea , un gráfico derivado de subconjuntos finitos de la junta apolínea
• Empaquetadura de esferas apolíneas , una generalización tridimensional de la empaquetadura apolínea
• Triángulo de Sierpiński , un fractal autosimilar con una estructura combinatoria similar

Notas

1. Satija, II, La mariposa en el mundo de Iglesias Waseas: La historia del fractal cuántico más fascinante ( Bristol : IOP Publishing , 2016), p. 5.
2. Boyd, David W. (1973), "La dimensión del conjunto residual del empaquetamiento apolíneo", Mathematika , 20 (2): 170–174, doi :10.1112/S0025579300004745, MR  0493763
3. McMullen, Curtis T. (1998), "Dimensión de Hausdorff y dinámica conforme, III: Cálculo de la dimensión" (PDF) , American Journal of Mathematics , 120 (4): 691–721, doi :10.1353/ajm.1998.0031, MR  1637951, S2CID  15928775
4. Conteo de círculos y teoría ergódica de grupos kleinianos por Hee Oh Brown. Universidad, diciembre de 2009
5. Ronald L. Graham, Jeffrey C. Lagarias, Colin M. Mallows, Alan R. Wilks y Catherine H. Yan; "Empaquetaduras del círculo apolíneo: teoría de números" J. Teoría de números, 100 (2003), 1-45
6. Bradford, Alden. "Revisitando las juntas apolíneas" . Consultado el 7 de agosto de 2022 .
7. Fuchs, Elena; Sanden, Katherine (28 de noviembre de 2011). "Algunos experimentos con empaquetamientos de círculos apolíneos integrales". Matemáticas experimentales . 20 (4): 380–399. arXiv : 1001.1406 . doi :10.1080/10586458.2011.565255. ISSN  1058-6458.
8. Summer Haag; Clyde Kertzer; James Rickards; Katherine E. Stange. "La conjetura local-global para los empaquetamientos de círculos apolíneos es falsa". arXiv : 2307.02749 .
9. Levy, Max G. (10 de agosto de 2023). "Dos estudiantes desentrañan una conjetura matemática ampliamente aceptada". Quanta Magazine . Consultado el 14 de agosto de 2023 .
10. Leibniz a Des Bosses, Hannover 11-17 de marzo de 1706, traducido por el Dr. Osvaldo Ottaviani https://humanities.technion.ac.il/en/leibniz-to-des-bosses-hannover-11-17-march-1706/
11. Kasner y Supnick 1943.

Referencias

• Benoit B. Mandelbrot : La geometría fractal de la naturaleza , WH Freeman, 1982, ISBN 0-7167-1186-9 
• Paul D. Bourke: "Introducción al fractal Apollony". Computers and Graphics, vol. 30, número 1, enero de 2006, páginas 134-136.
• Kasner, Edward ; Supnick, Fred (1943). "El empaquetamiento apolíneo de círculos". Actas de la Academia Nacional de Ciencias . 29 : 378–384.
• AA Kirillov : Una historia de dos fractales , Birkhauser, 2013.
• David Mumford , Caroline Series , David Wright: Las perlas de Indra: La visión de Felix Klein , Cambridge University Press, 2002, ISBN 0-521-35253-3 
• Jeffrey C. Lagarias, Colin L. Mallows, Allan R. Wilks: Más allá del teorema del círculo de Descartes , The American Mathematical Monthly, vol. 109, n.º 4 (abril de 2002), págs. 338-361, (arXiv:math.MG/0101066 v1 9 de enero de 2001)

Enlaces externos

• Weisstein, Eric W. "Junta apolínea". MathWorld .
• Alexander Bogomolny , Junta Apolínea , cortar el nudo
• Una junta apolínea interactiva que funciona con HTML5 puro en Wayback Machine (archivado el 2 de mayo de 2011)
• Un script de Matlab para trazar una junta apolínea 2D con n círculos idénticos Archivado el 7 de octubre de 2008 en Wayback Machine usando inversión de círculo
• Experimentos en línea con JSXGraph
• Junta apolínea de Michael Screiber, The Wolfram Demonstrations Project .
• Demostración interactiva de una junta apolínea ejecutándose en Java
• Dana Mackenzie. Computing Science: A Tisket, a Tasket, an Apollonian Gasket. American Scientist, enero/febrero de 2010.
• "El dibujo en la arena es la obra de arte más grande del mundo", The Telegraph , 16 de diciembre de 2009. Artículo de periódico sobre una obra de arte en forma de una junta apolínea parcial, con una circunferencia exterior de nueve millas.
• Juntas apolíneas dinámicas , Tartapelago de Giorgio Pietrocola, 2014. (en italiano)