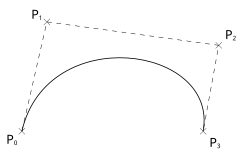
Spline

En el subcampo matemático del análisis numérico, un spline es una curva diferenciable definida en porciones mediante polinomios.En los problemas de interpolación, se utiliza a menudo la interpolación mediante splines porque da lugar a resultados similares requiriendo solamente el uso de polinomios de bajo grado, evitando así las oscilaciones, indeseables en la mayoría de las aplicaciones, encontradas al interpolar mediante polinomios de grado elevado.Para el ajuste de curvas, los splines se utilizan para aproximar formas complicadas.El término "spline" hace referencia a una amplia clase de funciones que son utilizadas en aplicaciones que requieren la interpolación de datos, o un suavizado de curvas.Los splines son utilizados para trabajar tanto en una como en varias dimensiones.Las funciones para la interpolación por splines normalmente se determinan como minimizadores de la aspereza sometidas a una serie de restricciones.En este artículo nos referiremos con el término "spline" a su versión restringida en una dimensión y polinomial, que es la más comúnmente utilizada.Este es el caso más sencillo.En él, vamos a interpolar una función f(x) de la que se nos dan un número N de paresEsta serie de funciones nuestras van a ser lineales, esto es, con grado 1: de la formaserá el conjunto de segmentos que unen nudos consecutivos; es por ello que nuestra función será continua en dichos puntos, pero no derivable en general.vale 1, 2 y 4 El primer segmentodeberá unir los primeros dos puntos de coordenadasReemplazando el valor de (b) en (1), se obtiene:deberá unir el segundo puntoa través de los que construimos el Spline tienen grado 2.Esto quiere decir, que va a tener la formason la cantidad de puntos sobre los que se define la función).La interpolación cuadrática nos va a asegurar que la función que nosotros generemos a trozos con los distintosva a ser continua, ya que para calcular los coeficientes que ajusten los polinomios a los puntos, vamos a determinar como condiciones: Esto sin embargo no es suficiente, y necesitamos una condición más.definida en tres puntos y dos ecuacionespara aproximarla, vamos a tener seis incógnitas en total.Para resolver esto necesitaríamos seis ecuaciones, pero vamos a tener tan sólo cinco: cuatro que igualan elen cada punto (dos por cada intervalo), y la quinta al igualar la derivada en el punto común a las dosEsto suele hacerse con el valor de la derivada en algún punto, al que se fuerza uno de losa través del que construimos los Splines enEsto quiere decir, que va a tener la formaEn este caso vamos a tener cuatro incógnitas por cada intervalo, y una nueva condición para cada punto común a dos intervalos, respecto a la derivada segunda: Como puede deducirse al compararlo con el caso de splines cuadráticos, ahora no nos va a faltar una sino dos ecuaciones (condiciones) para el número de incógnitas que tenemos.La forma de solucionar esto, determina el carácter de los splines cúbicos.