Ruptura espontánea de simetría

Cuando eso sucede el sistema no se comporta más de forma simétrica.Sin embargo, si el sistema solo tiene una dimensión espacial entonces solo las simetrías discretas pueden romperse en un estado vacío de la teoría cuántica, aunque también una solución clásica puede romper una simetría continua.Por ejemplo, en un campo eléctrico, las fuerzas sobre una partícula cargada son diferentes en diferentes direcciones, por lo que la simetría rotacional se rompe explícitamente por el campo eléctrico que no tiene esta simetría.Algunas excepciones notables son las fases topológicas de la materia, como el efecto Hall cuántico fraccionario.Por ejemplo, se espera que la densidad, la compresibilidad, el coeficiente de expansión térmica y el calor específico cambien cuando un líquido se convierte en sólido., no entonces se dice que el sistema tiene una "simetría en modo Goldstone" y conlleva la existencia de campos extras.[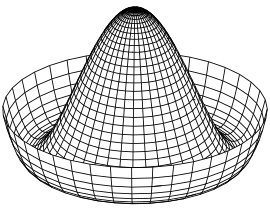4]​[5]​ Consideremos una cúpula simétrica ascendente con un canal que rodea la parte inferior.Si se coloca una bola en la cúspide de la cúpula, el sistema es simétrico con respecto a una rotación alrededor del eje central.Pero la bola puede romper espontáneamente esta simetría rodando por la cúpula hasta la depresión, un punto de mínima energía.Después, la pelota se detiene en un punto fijo del perímetro.La cúpula y la pelota conservan su simetría individual, pero el sistema no.[6]​ En el modelo relativista idealizado más sencillo, la simetría rota espontáneamente se resume mediante una teoría de campos escalares ilustrativa., que esencialmente dicta cómo se comporta un sistema, puede dividirse en términos cinéticos y potenciales,El sistema también tiene un estado de vacío inestable correspondiente a Φ = 0.Sin embargo, una vez que el sistema cae en un estado de vacío estable específico (que equivale a una elección de θ), esta simetría parecerá perderse, o "romperse espontáneamente".Este potencial tiene varios estados vacíos mínimos posibles dados por para alguna θ real entre 0 2π.El sistema también tiene un estado vacío inestable correspondiente a Φ = 0.Sin embargo, en cuanto el sistema cae en un estado vacío estable específico (correspondiente a la elección de θ) esta simetría se perderá o romperá espontáneamente.Generalmente, podemos tener ruptura espontánea de simetría en situaciones donde no hay estados vacíos y para sistemas que no están descritos por una acción (integral en el tiempo del lagrangiano).Si existe un campo que adquiere un valor de expectación (no necesariamente en el vacío) el cual no es invariante bajo la simetría en cuestión, decimos que el sistema está en una fase ordenada y la simetría se rompe espontáneamente.Esto se debe a que otros subsistemas interactúan con un parámetro de orden el cual forma un marco de referencia contra el cual se puede medir."Oculto" es un término mejor que "roto", porque la simetría siempre está ahí en estas ecuaciones.Makoto Kobayashi y Toshihide Maskawa compartieron con Yoichiro Nambu el premio por descubrir el origen de la ruptura de la simetría y su mecanismo.