Número
Un número es un objeto matemático utilizado para contar (cantidades), medir (magnitudes) y etiquetar.
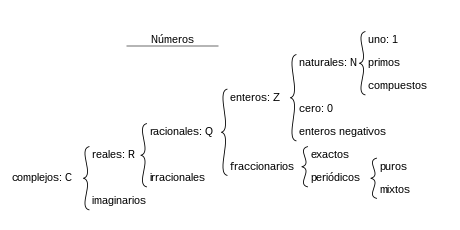
Los racionales junto con los irracionales forman el conjunto de los números reales, (ℝ).
, son conceptualmente los más simples y los que se usan para contar unidades discretas.
Durante un tiempo se pensó que toda magnitud física existente podía ser expresada en términos de números reales exclusivamente.
Además, en algunas aplicaciones prácticas, así como en las formulaciones estándar de la mecánica cuántica se considera útil introducir los números complejos.
Al parecer, la estructura matemática de los números complejos refleja estructuras existentes en problemas físicos, por lo que en física teórica y en diversas aplicaciones los números complejos se usan en pie de igualdad con los números reales, a pesar de que inicialmente fueron considerados únicamente como un artificio matemático sin relación con la realidad física.
fueron de alguna manera «descubiertos» o sugeridos en conexión con problemas planteados en problemas físicos o en el seno de la matemática elemental y todos ellos parecen tener importantes conexiones con la realidad física.
Tanto históricamente como conceptualmente, los diversos conjuntos numéricos, desde el más simple de los números naturales, hasta extensiones transcendentes de los números reales y complejos, elaboradas mediante la teoría de modelos durante el siglo XX, se construyen desde una estructura más simple hasta otra más compleja.
El sistema que se ha impuesto universalmente es la numeración posicional, gracias al invento del cero, con una base constante.
Peano, antes de establecer sus cinco proposiciones sobre los números naturales, explícita que supone sabida una definición (quizás debido a su «obviedad») de las palabras o conceptos cero, sucesor y número.
Básicamente la podemos clasificar en tres categorías: En este papiro adquirido por Alexander Henry Rhind (1833-1863) en 1858, cuyo contenido data del 2000 al 1800 a. C. además del sistema de numeración antes descrito nos encontramos con su tratamiento de las fracciones.
En las tablillas cuneiformes de la dinastía Hammurabi (1800-1600 a. C.) aparece el sistema posicional, antes referido, extendido a las fracciones, pero XXX vale para
Después, en la definición 5, da la famosa formulación de Eudoxo: «Dos magnitudes están en la misma razón
(definición que intercambiando el 2.º y 3.º términos equivale a nuestro procedimiento actual).
Hacia el siglo III a. C., en Grecia, se comenzó a representar la nada mediante una "o" que significa oudos 'vacío', y que no dio origen al concepto de cero como existe hoy en día.
La idea del cero como concepto matemático parece haber surgido en la India antes que en ningún otro lugar.
La única notación ordinal del Viejo Mundo fue la sumeria, donde el cero se representaba por un vacío.
Este último, conocido como Fibonacci, viajó por Oriente y aprendió de los árabes el sistema posicional hindú.
Escribió un libro, El Liber abaci, que trata en el capítulo I la numeración posicional, en los cuatro siguientes las operaciones elementales, en los capítulos VI y VII las fracciones: comunes, sexagesimales y unitarias (¡no usa los decimales, principal ventaja del sistema!
Pietro Antonio Cataldi (1548-1626), aunque con ejemplos numéricos, desarrolla una raíz cuadrada en fracciones continuas como hoy: Queremos calcular
Los números complejos eran en pocos casos aceptados como raíces o soluciones de ecuaciones (M. Stifel (1487-1567), S. Stevin (1548-1620)) y por casi ninguno como coeficientes).
Cardano en la resolución del problema dividir 10 en dos partes tales que su producto valga 40 obtiene como soluciones
Aunque se encuentra un uso más que casual de las fracciones decimales en la Arabia medieval y en la Europa renacentista, y ya en 1579 Vieta (1540-1603) proclamaba su apoyo a éstas frente a las sexagesimales, y las aceptaban los matemáticos que se dedicaban a la investigación, su uso se generalizó con la obra que Simon Stevin publicó en 1585 De Thiende (La Disme).
El siguiente se dice primera y su signo es (1) (segunda posición decimal 1/100).
La «,» también fue usada a comienzos del siglo XVII por el holandés Willebrord Snellius: 372,43.
Pascal (1623-1662) usó el método de inducción matemática, en su formulación abstracta, tal y como lo conocemos hoy, para probar propiedades relativas al triángulo numérico que lleva su nombre.
fue introducido por primera vez por Euler en 1777 y difundido por Gauss en su obra Disquisitiones arithmeticae de 1801.
Al identificar ahora los complejos con los puntos del plano los matemáticos se sentirán cómodos con estos números, ver es creer.
Euler ya hacía esta distinción en 1744 pero habría que esperar casi un siglo para que se estableciera claramente la existencia de los irracionales trascendentes en los trabajos de Liouville, Hermite y Lindeman.
Los sistemas puramente aritméticos recurren a bases donde cada signo recibe una interpretación diferente según su posición.