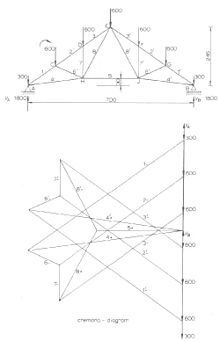
Diagrama de Cremona

El método fue popularizado por el matemático italianao Luigi Cremona a finales del siglo XIX.

[1]​ En la actualidad se sigue utilizando para los cálculos de reticulados (puentes, cerchas, marquesinas, etc.).

El método es aplicable a celosías trianguladas que sean estáticamente determinadas, lo cual implica que necesariamente el número de barras (b) y el número de nudos (n) o intersecciones de barras satisfaga la relación:

Puede demostrarse que la distancia entre dos puntos del diagrama de Cremona-Maxwell que definen una barra se corresponde con el esfuerzo axial de dicha barra en la estructura original.

Un diagrama de Cremona-Maxwell para una estructura reticular plana estáticamente determinada con fuerzas únicamente aplicadas sobre nudos de retículo se construye de acuerdo a las siguientes reglas: Una vez finalizado el proceso para una estructura de n nudos con b barras y f fuerzas formando r regiones, el diagrama de Cremona constará de r puntos, b+f segmentos (algunos puntos pueden ser dobles por lo que deben contarse con multiplicidad).