Ley de Gauss

Estos campos son aquellos cuya intensidad decrece como la distancia a la fuente al cuadrado.Sus fuentes son la carga eléctrica y la masa, respectivamente.La ley fue formulada por Carl Friedrich Gauss en 1835, pero no fue publicado hasta 1867.) es una propiedad de cualquier campo vectorial referida a una superficie hipotética que puede ser cerrada o abierta., cada uno de los cuales es lo suficientemente pequeño como para que pueda ser considerado como un plano.Estos elementos de área pueden ser representados como vectores, cuya magnitud es la propia área, la dirección es perpendicular a la superficie y hacia afuera.En cada cuadrado elemental también es posible trazar un vector de campo eléctricoYa que los cuadrados son tan pequeños como se quiera,puede considerarse constante en todos los puntos de un cuadrado dado.entre sí y la figura muestra una vista amplificada de dos cuadrados.Supóngase una superficie cilíndrica colocada dentro de un campo uniforme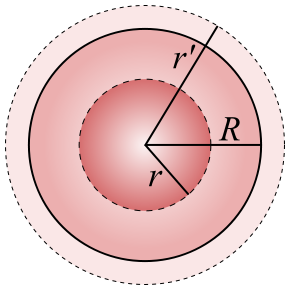Considérese una superficie esférica de radio r con una carga puntual q en su centro tal como muestra la figura., y el campo es constante en todos los puntos de la superficie esférica.Este teorema aplicado al campo eléctrico creado por una carga puntual es equivalente a la ley de Coulomb de la interacción electrostática.la unidad de este ángulo es el estereorradián (sr) Si el áreaComo la superficie que puede estar rodeando a la carga puede ser tan compleja como quiera, es mejor encontrar una relación sencilla para esta operación:de esta forma al sumar todos los flujos que atraviesan a la superficie queda:Esta ley se puede generalizar cuando hay un dieléctrico presente, introduciendo el campo de desplazamiento eléctricoes un elemento diferencial del área A sobre la cual se realiza la integral,Esta ley puede interpretarse, en electrostática, entendiendo el flujo como una medida del número de líneas de campo que atraviesan la superficie en cuestión.Además, al ser la densidad de líneas proporcional a la magnitud de la carga, resulta que este flujo es proporcional a la carga, si está encerrada, o nulo, si no lo está.Sea una recta cargada a lo largo del eje z. Tomemos como superficie cerrada un cilindro de radio r y altura h con su eje coincidente al eje z. Expresando el campo en coordenadas cilíndricas tenemos que debido a la simetría de reflexión respecto a un plano z=cte el campo no tiene componente en el eje z y la integración a las bases del cilindro no contribuye, de modo que aplicando la ley de Gauss: Debido a la simetría del problema el campo tendrá dirección radial y podemos sustituir el producto escalar por el producto de módulos (ya que la dirección de la superficie lateral también es radial).y teniendo en cuenta que según la ley de GaussPor lo tanto, para puntos interiores de la esfera: Y para puntos exteriores: En el caso de que la carga se distribuyera en la superficie de la esfera, es decir, en el caso de que fuera conductora, para puntos exteriores a la misma la intensidad del campo estaría dada por la segunda expresión, pero para puntos interiores a la esfera, el valor del campo sería nulo ya que la superficie gaussiana que se considerara no encerraría carga alguna.Al igual que para el campo eléctrico, existe una ley de Gauss para el magnetismo, que se expresa en sus formas integral y diferencial como Esta ley expresa la inexistencia de cargas magnéticas o, como se conocen habitualmente, monopolos magnéticos.- Es posible comparar ambas ya que podemos medir el flujo de propiedades que disminuyan con el cuadrado de la distancia , y esto lo tienen en común la fórmula del campo eléctrico con la del campo gravitatorio : Campo EléctricoUn dieléctrico, en presencia de un campo eléctrico, sufre lo que se llama polarización.La polarización consiste en la separación de las cargas positivas y negativas del dieléctrico, ya que el campo eléctrico acelera las cargas positivas en la dirección del campo y las negativas en la dirección opuesta.El material pasa a estar constituido por dipolos, como se muestra en la figura.