Combinación lineal

En matemáticas, particularmente en álgebra lineal, una combinación lineal es una expresión matemática que consiste en la suma entre pares de elementos, de determinados conjuntos, multiplicados entre sí.

En particular, la combinación lineal de un sistema de vectores se trata de un vector de la forma con los

elementos de un cuerpo.

La definición, provista de esta manera, da lugar a otras definiciones y herramientas importantes, como son los conceptos de independencia lineal y base de un espacio vectorial.

Dados dos conjuntos cualesquiera A y B.

Se define como combinación lineal a toda expresión de la forma

α b .

Resulta de especial interés la definición de combinación lineal de vectores con respecto a un conjunto de escalares.

Dado un espacio vectorial V sobre un cuerpo

de vectores en V, es decir,

Se dice que un vector

es combinación lineal de A si

{\displaystyle \exists k_{1},\dots ,k_{n}\in \mathbb {K} :v=\sum _{i=1}^{n}k_{i}v_{i}}

En términos no tan formales, diremos que

es combinación lineal de vectores de

si podemos expresarlo como una suma de productos por escalar de una cantidad finita de elementos de

En este caso, también se dice que

depende linealmente de los vectores de

En general, dado un vector v en un espacio vectorial, todo múltiplo suyo

λ v

es combinación lineal.

Para el caso particular

, sus múltiplos son vectores en el plano con la misma dirección, es decir, paralelos.

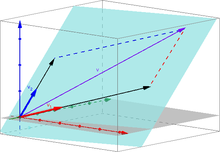
, decir que v es combinación lineal de otros dos vectores

no paralelos equivale a afirmar que los tres vectores son coplanarios, es decir, que se encuentran en un mismo plano.

Dado un conjunto de vectores A del espacio vectorial V, finito o infinito, se llama espacio generado, denotado como

{\displaystyle {\mbox{gen}}(A)=\left\{v\in V|\exists a_{1},\dots a_{n}\in \mathbb {K} ,\exists v_{1},\dots v_{n}\in A:v=\sum _{i=1}^{n}a_{i}v_{i}\right\}}

es el cuerpo sobre el cual está definido V.

En términos menos formales, el espacio generado a partir de A es el conjunto de todas las combinaciones lineales que pueden formarse con los vectores de A.

Dicho conjunto es el mínimo subespacio vectorial de V que contiene al conjunto A.