Copo de nieve de Koch

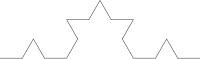
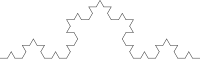
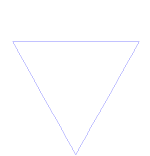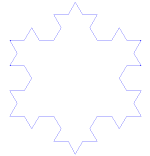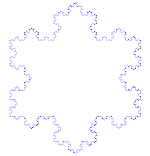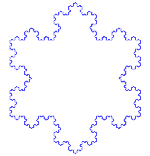
Su construcción más simple se realiza mediante un proceso iterativo que se inicia partiendo en tres un segmento de recta e insertando dos más en el tercero medio a manera de un triángulo equilátero, el proceso se repite infinidad de veces.Veamos el proceso que lleva a sustituir cada lado por la llamada curva de Koch: Se toma un segmento, se lo divide en tres partes iguales, se remplaza la parte central por dos partes de igual longitud haciendo un ángulo de 60 grados.La figura representa las seis primeras etapas de la construcción.Como el número de iteraciones tiende al infinito, el límite del perímetro es: donde |4/3| > 1.Existe una medida dimensional ln 4/ln 3, pero hasta ahora no se ha calculado.Expresado en términos de la longitud lateral s del triángulo original, esto es:[5]​Programa utilizando el módulo turtle, incluido en la biblioteca estándar de Python[6]​