Columna de Taylor
Una columna de Taylor es un fenómeno de la dinámica de fluidos que se produce como consecuencia del efecto Coriolis.
Debe su nombre a Geoffrey Ingram Taylor.
Los fluidos en rotación que son perturbados por un cuerpo sólido tienden a formar columnas paralelas al eje de rotación llamadas columnas de Taylor.
Un objeto que se mueve paralelo al eje de rotación en un fluido en rotación experimenta más fuerza de arrastre que la que experimentaría en un fluido sin rotación.
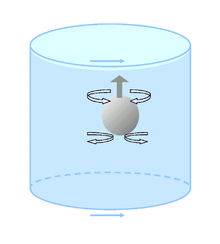
Por ejemplo, una pelota muy flotante (como una pelota de pingpong) subirá a la superficie más despacio que en un fluido no rotatorio.
Esto se debe a que el fluido en la trayectoria de la pelota que es empujado fuera del camino tiende a circular de vuelta al punto del que se aleja, debido al efecto Coriolis.
Cuanto mayor sea la velocidad de rotación, menor será el radio del círculo de inercia recorrido por el fluido.
En un fluido no giratorio, el fluido se separa por encima de la bola ascendente y se cierra por debajo de ella, ofreciendo relativamente poca resistencia a la bola.
En un fluido en rotación, la bola necesita empujar toda una columna de fluido por encima de ella y arrastrar toda una columna de fluido por debajo para subir a la superficie.
Por tanto, un fluido en rotación presenta cierto grado de rigidez.
Las columnas de Taylor fueron observadas por primera vez por William Thomson, Lord Kelvin, en 1868.
[1][2] Las columnas de Taylor aparecieron en conferencias demostrativas de Kelvin en 1881[3] y por John Perry en 1890.
[4] El fenómeno se explica mediante el teorema de Taylor-Proudman, y ha sido investigado por Taylor,[5] Grace,[6] Stewartson,[7] y Maxworthy[8]-entre otros.
Las columnas de Taylor han sido estudiadas con rigurosidad.
Para Re<<1, Ek<<1, Ro<<1, se ha deducido la ecuación de arrastre de un cilindro de radio, a halalndo la siguiente relación.
Para derivarla, Moore y Saffman resolvieron la ecuación de Navier–Stokes linealizada en coordenadas cilíndricas,[9] donde algunas de las componentes vericales y radiales del término viscoso se consideran pequeñas comparadas con el término de Coriolis:
u = ν
{\displaystyle 0=-{\frac {1}{\rho }}{\frac {\partial p}{\partial z}}+\nu \left({\frac {\partial ^{2}w}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial w}{\partial r}}\right)}
Para resolver estas ecuaciones, se incorpora la condición de conservación de volumen:
{\displaystyle {\frac {1}{r}}{\frac {\partial (ur)}{\partial r}}+{\frac {\partial w}{\partial z}}=0}
Se utiliza la relación de compatibilidad de Ekman para esta geometría para restringir la forma de la velocidad en la superficie del disco:
Los campos de velocidad resultantes se resuelven utilizando funciones de Bessel.
{\displaystyle u=-{\frac {\nu }{2\Omega }}\int \limits _{0}^{\infty }k^{2}A(k)J_{1}(kr)e^{-\nu k^{3}z/2\Omega }dk}
{\displaystyle v=\int \limits _{0}^{\infty }A(k)J_{1}(kr)e^{-\nu k^{3}z/2\Omega }dk}
{\displaystyle w=-\int \limits _{0}^{\infty }A(k)J_{0}(kr)e^{-\nu k^{3}z/2\Omega }dk}
Donde para cuando Ek<<1 la función A(k) se expresa como,
cos k a −
{\displaystyle A(k)={\frac {2Ua}{\pi }}\left(\cos ka-{\frac {\sin ka}{ka}}\right)}
La integración de la ecuación para v, se puede obtener la presión y por lo tanto la fuerza de arrastre queda expresada por la primera ecuación.