Fue desarrollado por David A. Huffman mientras era estudiante de doctorado en el MIT, y publicado en "A Method for the Construction of Minimum-Redundancy Codes".Posteriormente se encontró un método para llevar esto a cabo en un tiempo lineal si las probabilidades de los símbolos de entrada (también conocidas como "pesos") están ordenadas.Aunque la codificación de Huffman es óptima para una codificación símbolo a símbolo dada una distribución de probabilidad, su optimalidad a veces puede verse accidentalmente exagerada.Estos dos métodos pueden agrupar un número arbitrario de símbolos para una codificación más eficiente, y en general se adaptan a las estadísticas de entrada reales.M. Fano asignó las condiciones del trabajo bajo la premisa de encontrar el código binario más eficiente.Huffman, ante la imposibilidad de demostrar qué código era más eficiente, se rindió y empezó a estudiar para el examen final.Mientras estaba en este proceso vino a su mente la idea de usar árboles binarios de frecuencia ordenada y rápidamente probó que éste era el método más eficiente.l o n g i t u dSi no es el caso, siempre se puede derivar un código equivalente añadiendo símbolos extra (con probabilidades nulas asociadas), para hacer el código completo a la vez que se mantiene biunívoco.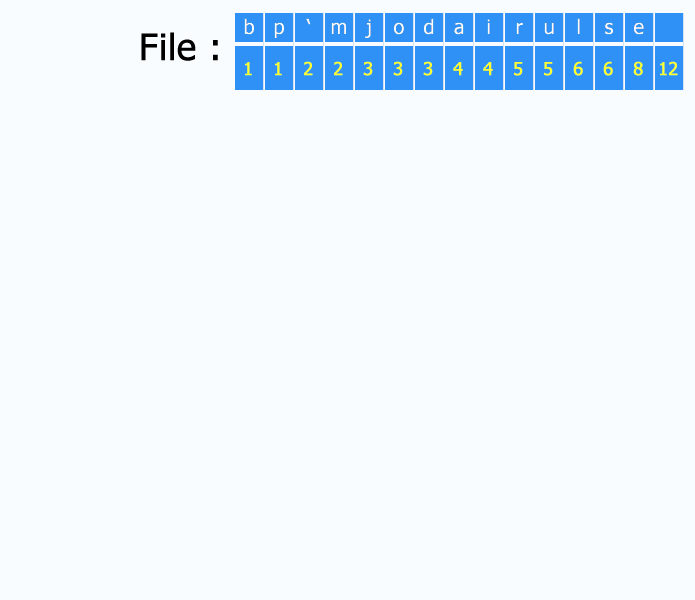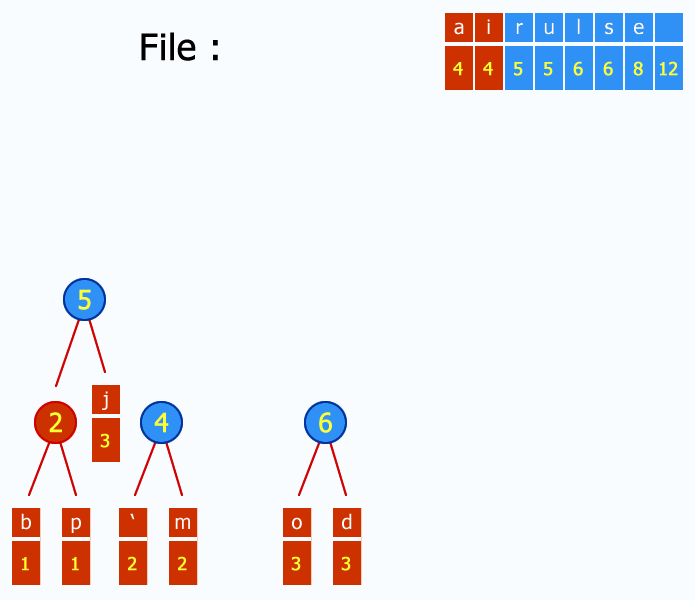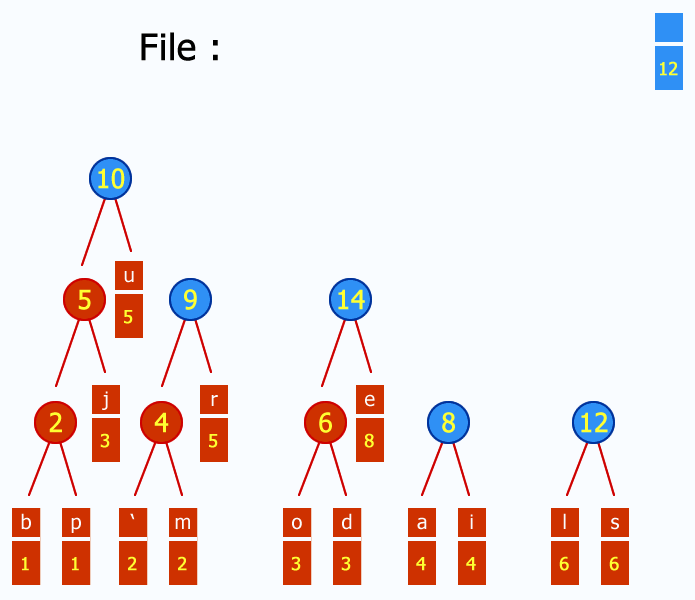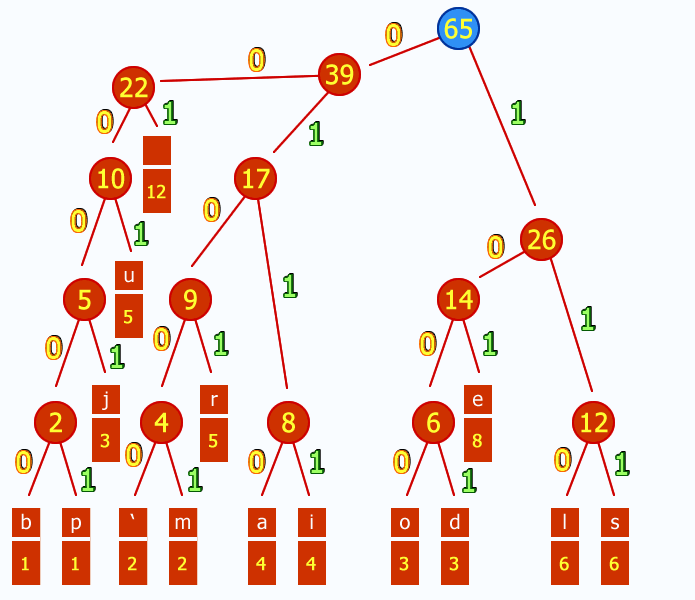Consiste en la creación de un árbol binario en el que se etiquetan los nodos hoja con los caracteres, junto a sus frecuencias, y de forma consecutiva se van uniendo cada pareja de nodos que menos frecuencia sumen, pasando a crear un nuevo nodo intermedio etiquetado con dicha suma.Se procede a realizar esta acción hasta que no quedan nodos hoja por unir a ningún nodo superior, y se ha formado el árbol binario.Posteriormente se etiquetan las aristas que unen cada uno de los nodos con ceros y unos (hijo derecho e izquierdo, respectivamente, por ejemplo).Los nodos contienen dos campos, el símbolo y el peso (frecuencia de aparición).El proceso de construcción del árbol comienza formando un nodo intermedio que agrupa a los dos nodos hoja que tienen menor peso (frecuencia de aparición).El proceso se repite hasta que solo quede un nodo en la lista.El algoritmo de construcción del árbol puede resumirse así: Aquí hay un ejemplo de construcción del árbol a partir del texto en francés "j'aime aller sur le bord de l'eau les jeudis ou les jours impairs": Las probabilidades usadas pueden ser genéricas para el dominio de la aplicación, que están basadas en el caso promedio, o pueden ser las frecuencias reales encontradas en el texto que se está comprimiendo.(Esta variación requiere que la tabla de frecuencias u otra estructura utilizada para la codificación deben ser almacenadas con el texto comprimido; las implementaciones emplean varios mecanismos para almacenar tablas de manera eficiente).Los códigos prefijos tienden a ser ligeramente ineficientes en alfabetos pequeños, donde las probabilidades normalmente se encuentran entre esos puntos óptimos.El "empaquetado", o expansión del tamaño del alfabeto concatenando múltiples símbolos en "palabras" de tamaño fijo o variable antes de la codificación Huffman, normalmente ayuda, especialmente cuando símbolos adyacentes están correlacionados (como en el caso de un texto en lenguaje natural).Existen muchas variaciones del código de Huffman, algunos que utilizan Huffman como algoritmo, y otros que encuentra el código prefijo óptimo.En el problema estándar de la codificación Huffman, se asume que cada símbolo del alfabeto con el que se construye cada palabra del código tiene igual costo de transmisión: una palabra del código cuya longitud sea N dígitos siempre tendrá un costo de N, sin importar cuántos de esos dígitos sean ceros, cuántos unos, etc. Cuando se trabaja bajo esta suposición, minimizar el costo total del mensaje y minimizar el número total de dígitos es lo mismo.En la codificación Huffman con costes desiguales la suposición anterior ya no es verdadera: los símbolos del alfabeto pueden tener longitudes no uniformes, debido a características del medio de transmisión.Un ejemplo es el alfabeto del código Morse, donde una 'raya' requiere más tiempo para ser enviada que un 'punto', y por lo tanto el costo del tiempo de transmisión de una raya es mayor.Si los pesos correspondientes a las entradas (ordenadas alfabéticamente) están en orden numérico, los códigos de Huffman tienen la misma longitud que los códigos alfabético óptimos, así que pueden calcularse como estas últimas, haciendo que la codificación Hu-Tucker sea innecesaria.Es Decir, ordenará descendentemente los símbolos según su peso, luego codificará según el método de Codificación Shannon-Fano, una vez obtenida la codificación se procede al armado del un Diagrama de flujo que comienza preguntando si el valor del primer bit del prefijo obtenido para el símbolo buscado es 0, del cual salen las 2 ramas, una para la afirmación y otra para la negación; luego seguirá preguntando para el segundo bit y derivará, para cada rama, a otra decisión o a un símbolo, según corresponda.Una sonda espacial ha sido lanzada al espacio para contar cierto tipo de perturbaciones estelares.A continuación se observa el código necesario para transmitir la siguiente serie de valores: Utilizando la codificación binaria, sería una serie de 60 bits; es decir, 3 bits por símbolo.nota: se ha añadido la misma serie separada en bloques con la única razón de facilitar una transcripción manual libre de errores para un estudio por parte del lector interesado.Es posible, también, apreciar cómo se pueden extraer sin ninguna ambigüedad los valores originales a partir de la cadena codificada mediante Huffman.Hay que añadir que la codificación de Huffman no puede ser aplicada a imágenes en blanco y negro porque es incapaz de producir compresión sobre un alfabeto binario.
Árbol de Huffman generado para las frecuencias de apariciones exactas del texto "ESTO ES UN EJEMPLO DE UN ARBOL DE HUFFMAN". Las frecuencias y códigos de cada carácter se muestran abajo. Codificar esta frase de 41 caracteres usando este código requiere 156 bits (sin contar con el espacio para el árbol) cuando con bytes de 8 bits requiere 328 bits.
