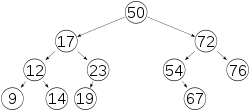
Árbol AVL

Fue el primer árbol de búsqueda binario auto-balanceable que se ideó., es: Cada nodo, además de la información que se pretende almacenar, debe tener los dos punteros a los árboles derecho e izquierdo, igual que los árboles binarios de búsqueda (ABB), y además el dato que controla el factor de equilibrio.Las operaciones básicas de un árbol AVL implican generalmente el realizar los mismos algoritmos que serían realizados en un árbol binario de búsqueda desequilibrado, pero precedido o seguido por una o más de las llamadas "rotaciones AVL".Pueden darse dos casos: rotación simple o rotación doble; a su vez ambos casos pueden ser hacia la derecha o hacia la izquierda.Si la inserción se produce en el hijo derecho del hijo izquierdo del nodo desequilibrado (o viceversa) hay que realizar una doble rotación.La inserción en un árbol de AVL puede ser realizada insertando el valor dado en el árbol como si fuera un árbol de búsqueda binario desequilibrado y después retrocediendo hacia la raíz, rotando sobre cualquier nodo que pueda haberse desequilibrado durante la inserción.Debido a que las rotaciones son una operación que tienen complejidad constante y a que la altura está limitada a O(log(n)), el tiempo de ejecución para la inserción es del orden O(log(n)).La diferencia se encuentra en el proceso de reequilibrado posterior.El problema de la extracción puede resolverse en O (log(n)) pasos.En el borrado pueden ser necesarias varias operaciones de restauración del equilibrio, y hay que seguir comprobando hasta llegar a la raíz.