En termodinámica , una propiedad molar aparente de un componente de una solución en una mezcla o solución es una cantidad definida con el propósito de aislar la contribución de cada componente a la no idealidad de la mezcla . Muestra el cambio en la propiedad de la solución correspondiente (por ejemplo, volumen ) por mol de ese componente agregado, cuando todo ese componente se agrega a la solución. Se describe como aparente porque parece representar la propiedad molar de ese componente en solución , siempre que se suponga que las propiedades de los otros componentes de la solución permanecen constantes durante la adición. Sin embargo, esta suposición a menudo no está justificada, ya que los valores de las propiedades molares aparentes de un componente pueden ser bastante diferentes de sus propiedades molares en estado puro.
Por ejemplo, el volumen de una solución que contiene dos componentes identificados [a] como disolvente y soluto está dado por
donde es el volumen del disolvente puro antes de añadir el soluto y su volumen molar (a la misma temperatura y presión que la solución), es el número de moles de disolvente, es el volumen molar aparente del soluto y es el número de moles del soluto en la solución. Al dividir esta relación por la cantidad molar de un componente, se puede obtener una relación entre la propiedad molar aparente de un componente y la proporción de mezcla de los componentes.
Esta ecuación sirve como definición de . El primer término es igual al volumen de la misma cantidad de disolvente sin soluto, y el segundo término es el cambio de volumen al añadir el soluto. puede entonces considerarse como el volumen molar del soluto si se supone que el volumen molar del disolvente no cambia con la adición de soluto. Sin embargo, esta suposición a menudo debe considerarse poco realista, como se muestra en los ejemplos siguientes, de modo que se describe solo como un valor aparente .
Una cantidad molar aparente se puede definir de manera similar para el componente identificado como solvente . Algunos autores han reportado volúmenes molares aparentes de ambos componentes (líquidos) de la misma solución. [1] [2] Este procedimiento se puede extender a mezclas ternarias y multicomponentes.
Las cantidades aparentes también se pueden expresar utilizando la masa en lugar del número de moles. Esta expresión produce cantidades específicas aparentes, como el volumen específico aparente.
donde las cantidades específicas se indican con letras minúsculas.
Las propiedades aparentes (molares) no son constantes (ni siquiera a una temperatura determinada), sino que son funciones de la composición. En caso de dilución infinita, una propiedad molar aparente y la propiedad molar parcial correspondiente se vuelven iguales.
Algunas propiedades molares aparentes que se utilizan comúnmente son la entalpía molar aparente, la capacidad calorífica molar aparente y el volumen molar aparente.
El volumen aparente (molal) de un soluto se puede expresar como una función de la molalidad b de ese soluto (y de las densidades de la solución y del solvente). El volumen de solución por mol de soluto es
Restando el volumen de disolvente puro por mol de soluto se obtiene el volumen molal aparente:
Para más solutos la igualdad anterior se modifica con la masa molar media de los solutos como si fueran un solo soluto con molalidad b T :
La suma de las molalidades de los productos – volúmenes molares aparentes de los solutos en sus soluciones binarias es igual al producto entre la suma de las molalidades de los solutos y el volumen molar aparente en la solución ternaria multicomponente mencionada anteriormente.
Se puede obtener una relación entre la molaridad aparente de un componente de una mezcla y la relación de mezcla molar dividiendo la relación de definición
al número de moles de un componente. Esto da la siguiente relación:
Obsérvense las definiciones contrastantes entre cantidad molar parcial y cantidad molar aparente: en el caso de volúmenes molares parciales , definidos por derivadas parciales
se puede escribir , y por lo tanto siempre se cumple. Por el contrario, en la definición de volumen molar aparente, se utiliza en su lugar el volumen molar del disolvente puro, , que se puede escribir como
para comparar. En otras palabras, suponemos que el volumen del disolvente no cambia y utilizamos el volumen molar parcial donde el número de moles del soluto es exactamente cero ("el volumen molar"). Por lo tanto, en la expresión que define el volumen molar aparente ,
El término se atribuye al disolvente puro, mientras que el volumen sobrante, , se considera que proviene del soluto. A una dilución alta con , tenemos , y por lo tanto el volumen molar aparente y el volumen molar parcial del soluto también convergen: .
Cuantitativamente, la relación entre las propiedades molares parciales y las aparentes se puede derivar de la definición de las cantidades aparentes y de la molalidad. Para el volumen,
La relación r a entre el volumen molar aparente de un electrolito disuelto en una solución concentrada y el volumen molar del solvente (agua) se puede vincular al componente estadístico del coeficiente de actividad del electrolito y su número de capa de solvatación h : [3]
donde ν es el número de iones debido a la disociación del electrolito y b es la molalidad como se indicó anteriormente.

El volumen molar aparente de la sal suele ser menor que el volumen molar de la sal sólida. Por ejemplo, el NaCl sólido tiene un volumen de 27 cm3 por mol, pero el volumen molar aparente a bajas concentraciones es de solo 16,6 cc/mol. De hecho, algunos electrolitos acuosos tienen volúmenes molares aparentes negativos: NaOH −6,7, LiOH −6,0 y Na 2 CO 3 −6,7 cm3 / mol. [4] Esto significa que sus soluciones en una cantidad dada de agua tienen un volumen menor que la misma cantidad de agua pura. (El efecto es pequeño, sin embargo). La razón física es que las moléculas de agua cercanas son fuertemente atraídas por los iones, de modo que ocupan menos espacio.
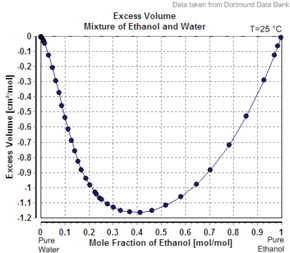
Otro ejemplo del volumen molar aparente del segundo componente es menor que su volumen molar como sustancia pura es el caso del etanol en agua. Por ejemplo, con un 20 por ciento en masa de etanol, la solución tiene un volumen de 1,0326 litros por kg a 20 °C, mientras que el agua pura es de 1,0018 L/kg (1,0018 cc/g). [5] El volumen aparente del etanol añadido es de 1,0326 L – 0,8 kg x 1,0018 L/kg = 0,2317 L. El número de moles de etanol es de 0,2 kg / (0,04607 kg/mol) = 4,341 mol, de modo que el volumen molar aparente es de 0,2317 L / 4,341 mol = 0,0532 L / mol = 53,2 cc/mol (1,16 cc/g). Sin embargo, el etanol puro tiene un volumen molar a esta temperatura de 58,4 cc/mol (1,27 cc/g).
Si la solución fuera ideal , su volumen sería la suma de los componentes no mezclados. El volumen de 0,2 kg de etanol puro es 0,2 kg x 1,27 L/kg = 0,254 L, y el volumen de 0,8 kg de agua pura es 0,8 kg x 1,0018 L/kg = 0,80144 L, por lo que el volumen de la solución ideal sería 0,254 L + 0,80144 L = 1,055 L. La no idealidad de la solución se refleja en una ligera disminución (aproximadamente 2,2%, 1,0326 en lugar de 1,055 L/kg) en el volumen del sistema combinado al mezclar. A medida que el porcentaje de etanol aumenta hacia el 100%, el volumen molar aparente aumenta hasta el volumen molar del etanol puro.
Las cantidades aparentes pueden subrayar las interacciones en sistemas electrolito-no electrolito que muestran interacciones como la entrada y salida de sal , pero también brindan información sobre las interacciones ion-ion, especialmente por su dependencia de la temperatura.
En el caso de soluciones multicomponentes, las propiedades molares aparentes se pueden definir de varias maneras. Para el volumen de una solución ternaria (de 3 componentes) con un disolvente y dos solutos, por ejemplo, todavía habría una sola ecuación , que es insuficiente para determinar los dos volúmenes aparentes. (Esto contrasta con las propiedades molares parciales , que son propiedades intensivas bien definidas de los materiales y, por lo tanto, definidas de forma inequívoca en sistemas multicomponentes. Por ejemplo, el volumen molar parcial se define para cada componente i como ).
Una descripción de las soluciones acuosas ternarias considera únicamente el volumen molar aparente medio ponderado de los solutos, [6] definido como
donde es el volumen de la solución y el volumen de agua pura. Este método se puede extender a mezclas con más de 3 componentes. [7]
La suma de las molalidades de los productos – volúmenes molares aparentes de los solutos en sus soluciones binarias es igual al producto entre la suma de las molalidades de los solutos y el volumen molar aparente en la solución ternaria multicomponente mencionada anteriormente.
Otro método es tratar el sistema ternario como pseudobinario y definir el volumen molar aparente de cada soluto con referencia a un sistema binario que contiene ambos otros componentes: agua y el otro soluto. [8] Los volúmenes molares aparentes de cada uno de los dos solutos son entonces
El volumen molar aparente del disolvente es:
Sin embargo, esta es una descripción insatisfactoria de las propiedades volumétricas. [9]
El volumen molar aparente de dos componentes o solutos considerados como un pseudocomponente no debe confundirse con los volúmenes de mezclas binarias parciales con un componente común V ij , V jk que mezclados en una determinada proporción forman una determinada mezcla ternaria V o V ijk . [ aclaración necesaria ]
Por supuesto, el volumen complementario de un componente con respecto a otros componentes de la mezcla se puede definir como una diferencia entre el volumen de la mezcla y el volumen de una submezcla binaria de una composición dada como:
Existen situaciones en las que no existe una forma rigurosa de definir cuál es el solvente y cuál el soluto, como en el caso de las mezclas líquidas (por ejemplo, agua y etanol) que pueden disolver o no un sólido como el azúcar o la sal. En estos casos, las propiedades molares aparentes pueden y deben atribuirse a todos los componentes de la mezcla.