La representación n -vector (también llamada normal geodésica o vector normal elipsoide ) es una representación no singular de tres parámetros muy adecuada para reemplazar las coordenadas geodésicas ( latitud y longitud ) para la representación de la posición horizontal en cálculos matemáticos y algoritmos informáticos.
Geométricamente, el vector n para una posición dada en un elipsoide es el vector unitario que apunta hacia afuera y que es normal en esa posición al elipsoide. Para representar posiciones horizontales en la Tierra, el elipsoide es un elipsoide de referencia y el vector se descompone en un sistema de coordenadas centrado en la Tierra y fijo en ella . Se comporta de manera uniforme en todas las posiciones de la Tierra y mantiene la propiedad matemática de uno a uno .
En términos más generales, el concepto se puede aplicar para representar posiciones en el límite de un subconjunto estrictamente convexo y acotado de un espacio euclidiano de dimensión k , siempre que dicho límite sea una variedad diferenciable . En este caso general, el vector n consta de k parámetros.
Un vector normal a una superficie estrictamente convexa se puede utilizar para definir de forma única la posición de una superficie. El vector n es un vector normal que apunta hacia afuera con una longitud unitaria que se utiliza como representación de la posición. [1]
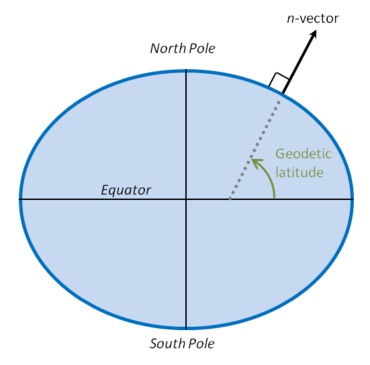
Para la mayoría de las aplicaciones, la superficie es el elipsoide de referencia de la Tierra y, por lo tanto, se utiliza el vector n para representar una posición horizontal. Por lo tanto, el ángulo entre el vector n y el plano ecuatorial corresponde a la latitud geodésica , como se muestra en la figura.
Una posición de superficie tiene dos grados de libertad , y por lo tanto dos parámetros son suficientes para representar cualquier posición en la superficie. En el elipsoide de referencia, la latitud y la longitud son parámetros comunes para este propósito, pero como todas las representaciones de dos parámetros , tienen singularidades . Esto es similar a la orientación , que tiene tres grados de libertad, pero todas las representaciones de tres parámetros tienen singularidades. [2] En ambos casos, las singularidades se evitan agregando un parámetro adicional, es decir, usar n -vector (tres parámetros) para representar la posición horizontal y un cuaternión unitario (cuatro parámetros) para representar la orientación .
Un n -vector es una representación uno a uno , lo que significa que cualquier posición de superficie corresponde a un n -vector único, y cualquier n -vector corresponde a una posición de superficie única.
Como vector euclidiano 3D , se puede utilizar el álgebra vectorial 3D estándar para los cálculos de posición, y esto hace que el vector n sea adecuado para la mayoría de los cálculos de posición horizontal.
A partir de la definición del sistema de coordenadas ECEF , denominado e , es claro que pasar de latitud/longitud a n -vector, se logra:
El superíndice e significa que el vector n está descompuesto en el sistema de coordenadas e (es decir, el primer componente es la proyección escalar del vector n sobre el eje x de e , el segundo sobre el eje y de e, etc.). Nótese que la ecuación es exacta tanto para el modelo de Tierra esférico como para el elipsoidal.
A partir de los tres componentes del vector n , , , y , la latitud se puede encontrar utilizando:
La expresión más a la derecha es la más adecuada para la implementación de un programa informático. [1]
La longitud se encuentra utilizando:
En estas expresiones se debe implementar una llamada a atan2 ( y , x ). La singularidad de longitud del polo es evidente ya que atan2 (0,0) no está definido. Nótese que las ecuaciones son exactas tanto para el modelo de la Tierra esférica como para el elipsoidal.
Para hallar la distancia ortodrómica entre dos posiciones horizontales (suponiendo que la Tierra es esférica) se suele utilizar la latitud y la longitud. Hay tres expresiones comunes para esta distancia: la primera se basa en arccos , la segunda en arcsin y la última en arctan . Las expresiones, que son cada vez más complejas para evitar inestabilidades numéricas , no son fáciles de hallar y, puesto que se basan en la latitud y la longitud, las singularidades de los polos pueden convertirse en un problema. También contienen deltas de latitud y longitud, que en general se deben utilizar con cuidado cerca del meridiano ±180° y de los polos.
Resolver el mismo problema utilizando n -vectores es más sencillo debido a la posibilidad de utilizar álgebra vectorial . La expresión arccos se obtiene a partir del producto escalar , mientras que la magnitud del producto vectorial da la expresión arcsin. Combinando los dos se obtiene la expresión arctan: [1]
donde y son los n -vectores que representan las dos posiciones a y b . es la diferencia angular y, por lo tanto, la distancia del círculo máximo se obtiene multiplicando por el radio de la Tierra. Esta expresión también funciona en los polos y en el meridiano ±180°.
Hay varios otros ejemplos en los que el uso del álgebra vectorial simplifica los problemas estándar. [1] Para una comparación general de las diversas representaciones, consulte la página de representaciones de posición horizontal .