Óptica geométrica

Modelo de óptica que describe la luz como rayos geométricos.

La óptica geométrica , u óptica de rayos , es un modelo de la óptica que describe la propagación de la luz en términos de rayos . El rayo en la óptica geométrica es una abstracción útil para aproximar las trayectorias por las que se propaga la luz en determinadas circunstancias.

Los supuestos simplificadores de la óptica geométrica incluyen que los rayos de luz:

• se propagan en trayectorias en línea recta a medida que viajan en un medio homogéneo
• doblarse, y en circunstancias particulares puede dividirse en dos, en la interfaz entre dos medios diferentes
• siguen trayectorias curvas en un medio en el que el índice de refracción cambia
• Puede ser absorbida o reflejada.

La óptica geométrica no tiene en cuenta ciertos efectos ópticos como la difracción y la interferencia , que sí se tienen en cuenta en la óptica física . Esta simplificación es útil en la práctica; es una aproximación excelente cuando la longitud de onda es pequeña en comparación con el tamaño de las estructuras con las que interactúa la luz. Las técnicas son particularmente útiles para describir aspectos geométricos de la formación de imágenes , incluidas las aberraciones ópticas .

Explicación

A medida que la luz viaja a través del espacio, oscila en amplitud . En esta imagen, cada cresta de amplitud máxima está marcada con un plano para ilustrar el frente de onda . El rayo es la flecha perpendicular a estas superficies paralelas .

Un rayo de luz es una línea o curva perpendicular a los frentes de onda de la luz (y por lo tanto colineal con el vector de onda ). Una definición un poco más rigurosa de un rayo de luz se desprende del principio de Fermat , que establece que el camino recorrido entre dos puntos por un rayo de luz es el camino que puede recorrer en el menor tiempo posible. ^[1]

La óptica geométrica suele simplificarse mediante la aproximación paraxial o "aproximación de ángulo pequeño". El comportamiento matemático se vuelve entonces lineal , lo que permite describir los componentes y sistemas ópticos mediante matrices simples. Esto conduce a las técnicas de óptica gaussiana y trazado de rayos paraxial , que se utilizan para encontrar propiedades básicas de los sistemas ópticos, como la posición aproximada de imágenes y objetos y los aumentos . ^[2]

Reflexión

Diagrama de reflexión especular

Las superficies brillantes, como los espejos, reflejan la luz de una manera sencilla y predecible. Esto permite la producción de imágenes reflejadas que pueden asociarse con una ubicación real o extrapolada ( virtual ) en el espacio.

En este tipo de superficies, la dirección del rayo reflejado está determinada por el ángulo que forma el rayo incidente con la normal a la superficie , una línea perpendicular a la superficie en el punto donde incide el rayo. Los rayos incidente y reflejado se encuentran en un mismo plano, y el ángulo entre el rayo reflejado y la normal a la superficie es el mismo que el que existe entre el rayo incidente y la normal. ^[3] Esto se conoce como la Ley de Reflexión .

En el caso de los espejos planos , la ley de reflexión implica que las imágenes de los objetos están en posición vertical y a la misma distancia detrás del espejo que los objetos que están frente a él. El tamaño de la imagen es el mismo que el del objeto (el aumento de un espejo plano es igual a uno). La ley también implica que las imágenes especulares están invertidas en paridad , lo que se percibe como una inversión de izquierda a derecha.

Los espejos con superficies curvas se pueden modelar mediante trazado de rayos y utilizando la ley de reflexión en cada punto de la superficie. Para los espejos con superficies parabólicas , los rayos paralelos que inciden en el espejo producen rayos reflejados que convergen en un foco común . Otras superficies curvas también pueden enfocar la luz, pero con aberraciones debido a la forma divergente que hace que el foco se difumine en el espacio. En particular, los espejos esféricos exhiben aberración esférica . Los espejos curvos pueden formar imágenes con un aumento mayor o menor que uno, y la imagen puede ser vertical o invertida. Una imagen vertical formada por reflexión en un espejo siempre es virtual, mientras que una imagen invertida es real y puede proyectarse en una pantalla. ^[3]

Refracción

Ilustración de la ley de Snell

La refracción ocurre cuando la luz viaja a través de un área del espacio que tiene un índice de refracción cambiante. El caso más simple de refracción ocurre cuando hay una interfaz entre un medio uniforme con índice de refracción y otro medio con índice de refracción . En tales situaciones, la Ley de Snell describe la desviación resultante del rayo de luz: donde y son los ángulos entre la normal (a la interfaz) y las ondas incidente y refractada, respectivamente. Este fenómeno también está asociado con un cambio en la velocidad de la luz como se ve a partir de la definición de índice de refracción proporcionada anteriormente, que implica: donde y son las velocidades de onda a través de los respectivos medios. ^[3] ${\displaystyle n_{1}}$ ${\displaystyle n_{2}}$ $${\displaystyle n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}}$$ ${\displaystyle \theta _{1}}$ ${\displaystyle \theta _{2}}$ $${\displaystyle v_{1}\sin \theta _{2}\ =v_{2}\sin \theta _{1}}$$ ${\displaystyle v_{1}}$ ${\displaystyle v_{2}}$

Entre las diversas consecuencias de la Ley de Snell se incluye el hecho de que, en el caso de los rayos de luz que viajan desde un material con un alto índice de refracción a un material con un bajo índice de refracción, es posible que la interacción con la interfaz dé como resultado una transmisión cero. Este fenómeno se denomina reflexión interna total y permite la tecnología de fibra óptica . A medida que las señales de luz viajan por un cable de fibra óptica, experimentan una reflexión interna total, lo que permite que prácticamente no se pierda luz a lo largo del cable. También es posible producir rayos de luz polarizados utilizando una combinación de reflexión y refracción: cuando un rayo refractado y el rayo reflejado forman un ángulo recto , el rayo reflejado tiene la propiedad de "polarización plana". El ángulo de incidencia necesario para tal escenario se conoce como ángulo de Brewster . ^[3]

La ley de Snell se puede utilizar para predecir la desviación de los rayos de luz a medida que pasan a través de "medios lineales" siempre que se conozcan los índices de refracción y la geometría de los medios. Por ejemplo, la propagación de la luz a través de un prisma hace que el rayo de luz se desvíe dependiendo de la forma y la orientación del prisma. Además, dado que las diferentes frecuencias de luz tienen índices de refracción ligeramente diferentes en la mayoría de los materiales, la refracción se puede utilizar para producir espectros de dispersión que aparecen como arcoíris. El descubrimiento de este fenómeno al pasar la luz a través de un prisma se atribuye a Isaac Newton . ^[3]

Algunos medios tienen un índice de refracción que varía gradualmente con la posición y, por lo tanto, los rayos de luz se curvan a través del medio en lugar de viajar en línea recta. Este efecto es el responsable de los espejismos que se ven en los días calurosos, donde el índice de refracción cambiante del aire hace que los rayos de luz se doblen creando la apariencia de reflejos especulares en la distancia (como si estuvieran en la superficie de un estanque de agua). El material que tiene un índice de refracción variable se denomina material de índice de gradiente (GRIN) y tiene muchas propiedades útiles que se utilizan en las tecnologías de escaneo óptico modernas, incluidas las fotocopiadoras y los escáneres . El fenómeno se estudia en el campo de la óptica de índice de gradiente . ^[4]

Un diagrama de trazado de rayos para una lente convergente simple.

Un dispositivo que produce rayos de luz convergentes o divergentes debido a la refracción se conoce como lente . Las lentes delgadas producen puntos focales en cada lado que se pueden modelar utilizando la ecuación del fabricante de lentes . ^[5] En general, existen dos tipos de lentes: lentes convexas , que hacen que los rayos de luz paralelos converjan, y lentes cóncavas , que hacen que los rayos de luz paralelos diverjan. La predicción detallada de cómo se producen las imágenes con estas lentes se puede hacer utilizando el trazado de rayos similar a los espejos curvos. De manera similar a los espejos curvos, las lentes delgadas siguen una ecuación simple que determina la ubicación de las imágenes dada una longitud focal particular ( ) y una distancia del objeto ( ): donde es la distancia asociada con la imagen y se considera por convención como negativa si está en el mismo lado de la lente que el objeto y positiva si está en el lado opuesto de la lente. ^[5] La longitud focal f se considera negativa para lentes cóncavas. ${\displaystyle f}$ ${\displaystyle S_{1}}$ $${\displaystyle {\frac {1}{S_{1}}}+{\frac {1}{S_{2}}}={\frac {1}{f}}}$$ ${\displaystyle S_{2}}$

Los rayos paralelos entrantes son enfocados por una lente convexa en una imagen real invertida a una distancia focal de la lente, en el lado más alejado de la lente.

Los rayos paralelos entrantes son enfocados por una lente convexa en una imagen real invertida a una distancia focal de la lente, en el lado más alejado de la lente.

Los rayos que provienen de un objeto situado a una distancia finita se enfocan a una distancia mayor de la lente que la distancia focal; cuanto más cerca está el objeto de la lente, más lejos está la imagen de la lente. En las lentes cóncavas, los rayos paralelos que llegan divergen después de atravesar la lente, de tal manera que parecen haberse originado en una imagen virtual vertical a una distancia focal de la lente, en el mismo lado de la lente por el que se aproximan los rayos paralelos.

En las lentes cóncavas, los rayos paralelos entrantes divergen después de pasar por la lente, de tal manera que parecen haberse originado en una imagen virtual vertical a una distancia focal de la lente, en el mismo lado de la lente por el que se aproximan los rayos paralelos.

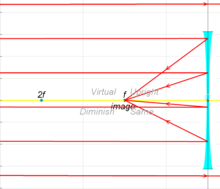
Los rayos que provienen de un objeto a una distancia finita se asocian con una imagen virtual que está más cerca de la lente que la distancia focal y del mismo lado de la lente que el objeto. Cuanto más cerca esté el objeto de la lente, más cerca estará la imagen virtual de la lente.

Los rayos de un objeto a una distancia finita se asocian con una imagen virtual que está más cerca de la lente que la distancia focal y en el mismo lado de la lente que el objeto.

De la misma manera, el aumento de una lente se obtiene mediante la fórmula , donde el signo negativo se da, por convención, para indicar un objeto en posición vertical para valores positivos y un objeto invertido para valores negativos. De manera similar a los espejos, las imágenes en posición vertical producidas por lentes individuales son virtuales, mientras que las imágenes invertidas son reales. ^[3] $${\displaystyle M=-{\frac {S_{2}}{S_{1}}}={\frac {f}{f-S_{1}}}}$$

Las lentes sufren aberraciones que distorsionan las imágenes y los puntos focales. Estas se deben tanto a imperfecciones geométricas como al cambio del índice de refracción para las diferentes longitudes de onda de la luz ( aberración cromática ). ^[3]

Matemáticas subyacentes

Como estudio matemático, la óptica geométrica surge como un límite de longitud de onda corta para soluciones de ecuaciones diferenciales parciales hiperbólicas (método de Sommerfeld-Runge) o como una propiedad de propagación de discontinuidades de campo según las ecuaciones de Maxwell (método de Luneburg). En este límite de longitud de onda corta, es posible aproximar la solución localmente mediante donde satisfacen una relación de dispersión , y la amplitud varía lentamente. Más precisamente, la solución de orden principal toma la forma La fase se puede linealizar para recuperar un gran número de onda , y frecuencia . La amplitud satisface una ecuación de transporte . El pequeño parámetro entra en escena debido a condiciones iniciales altamente oscilatorias. Por lo tanto, cuando las condiciones iniciales oscilan mucho más rápido que los coeficientes de la ecuación diferencial, las soluciones serán altamente oscilatorias y se transportarán a lo largo de los rayos. Suponiendo que los coeficientes en la ecuación diferencial sean suaves, los rayos también lo serán. En otras palabras, no se produce refracción . La motivación de esta técnica surge del estudio del escenario típico de propagación de la luz, donde la luz de longitud de onda corta viaja a lo largo de rayos que minimizan (más o menos) su tiempo de viaje. Su aplicación completa requiere herramientas de análisis microlocal . $${\displaystyle u(t,x)\approx a(t,x)e^{i(k\cdot x-\omega t)}}$$ ${\displaystyle k,\omega }$ ${\displaystyle a(t,x)}$ $${\displaystyle a_{0}(t,x)e^{i\varphi (t,x)/\varepsilon }.}$$ ${\displaystyle \varphi (t,x)/\varepsilon }$ ${\displaystyle k:=\nabla _{x}\varphi }$ ${\displaystyle \omega :=-\partial _{t}\varphi }$ ${\displaystyle a_{0}}$ ${\displaystyle \varepsilon \,}$

Método Sommerfeld-Runge

El método de obtención de ecuaciones de óptica geométrica tomando el límite de longitud de onda cero fue descrito por primera vez por Arnold Sommerfeld y J. Runge en 1911. ^[6] Su derivación se basó en una observación oral de Peter Debye . ^{[7] [8]} Consideremos un campo escalar monocromático , donde podría ser cualquiera de los componentes del campo eléctrico o magnético y, por lo tanto, la función satisface la ecuación de onda donde siendo la velocidad de la luz en el vacío. Aquí, es el índice de refracción del medio. Sin pérdida de generalidad, introduzcamos para convertir la ecuación a ${\displaystyle \psi (\mathbf {r} ,t)=\phi (\mathbf {r} )e^{i\omega t}}$ ${\displaystyle \psi }$ ${\displaystyle \phi }$ $${\displaystyle \nabla ^{2}\phi +k_{o}^{2}n(\mathbf {r} )^{2}\phi =0}$$ ${\displaystyle k_{o}=\omega /c=2\pi /\lambda _{o}}$ ${\displaystyle c}$ ${\displaystyle n(\mathbf {r} )}$ ${\displaystyle \phi =A(k_{o},\mathbf {r} )e^{ik_{o}S(\mathbf {r} )}}$ $${\displaystyle -k_{o}^{2}A[(\nabla S)^{2}-n^{2}]+2ik_{o}(\nabla S\cdot \nabla A)+ik_{o}A\nabla ^{2}S+\nabla ^{2}A=0.}$$

Dado que el principio subyacente de la óptica geométrica se encuentra en el límite , se supone la siguiente serie asintótica, ${\displaystyle \lambda _{o}\sim k_{o}^{-1}\rightarrow 0}$ $${\displaystyle A(k_{o},\mathbf {r} )=\sum _{m=0}^{\infty }{\frac {A_{m}(\mathbf {r} )}{(ik_{o})^{m}}}}$$

Para valores grandes pero finitos de , la serie diverge, y hay que tener cuidado de mantener solo los primeros términos apropiados. Para cada valor de , se puede encontrar un número óptimo de términos que se deben mantener y agregar más términos que el número óptimo puede dar como resultado una aproximación más pobre. ^[9] Sustituyendo la serie en la ecuación y reuniendo términos de diferentes órdenes, se encuentra en general, ${\displaystyle k_{o}}$ ${\displaystyle k_{o}}$ $${\displaystyle {\begin{aligned}O(k_{o}^{2}):&\quad (\nabla S)^{2}=n^{2},\\[1ex]O(k_{o}):&\quad 2\nabla S\cdot \nabla A_{0}+A_{0}\nabla ^{2}S=0,\\[1ex]O(1):&\quad 2\nabla S\cdot \nabla A_{1}+A_{1}\nabla ^{2}S=-\nabla ^{2}A_{0},\end{aligned}}}$$ $${\displaystyle O(k_{o}^{1-m}):\quad 2\nabla S\cdot \nabla A_{m}+A_{m}\nabla ^{2}S=-\nabla ^{2}A_{m-1}.}$$

La primera ecuación se conoce como ecuación eikonal , que determina que la eikonal es una ecuación de Hamilton-Jacobi , escrita por ejemplo en coordenadas cartesianas se convierte en ${\displaystyle S(\mathbf {r} )}$ $${\displaystyle \left({\frac {\partial S}{\partial x}}\right)^{2}+\left({\frac {\partial S}{\partial y}}\right)^{2}+\left({\frac {\partial S}{\partial z}}\right)^{2}=n^{2}.}$$

Las ecuaciones restantes determinan las funciones . ${\displaystyle A_{m}(\mathbf {r} )}$

Método de Lüneburg

El método de obtención de ecuaciones de óptica geométrica mediante el análisis de superficies de discontinuidades de soluciones a las ecuaciones de Maxwell fue descrito por primera vez por Rudolf Karl Luneburg en 1944. ^[10] No restringe el campo electromagnético a tener una forma especial requerida por el método de Sommerfeld-Runge que supone que la amplitud y la fase satisfacen la ecuación . Esta condición se satisface, por ejemplo, con ondas planas, pero no es aditiva. ${\displaystyle A(k_{o},\mathbf {r} )}$ ${\displaystyle S(\mathbf {r} )}$ ${\textstyle \lim _{k_{0}\to \infty }{\frac {1}{k_{0}}}\left({\frac {1}{A}}\,\nabla S\cdot \nabla A+{\frac {1}{2}}\nabla ^{2}S\right)=0}$

La principal conclusión del enfoque de Luneburg es la siguiente:

Teorema. Supóngase que los campos y (en un medio isótropo lineal descrito por las constantes dieléctricas y ) tienen discontinuidades finitas a lo largo de una superficie (móvil) en descrita por la ecuación . Entonces las ecuaciones de Maxwell en forma integral implican que satisface la ecuación eikonal : donde es el índice de refracción del medio (unidades gaussianas). ${\displaystyle \mathbf {E} (x,y,z,t)}$ ${\displaystyle \mathbf {H} (x,y,z,t)}$ ${\displaystyle \varepsilon (x,y,z)}$ ${\displaystyle \mu (x,y,z)}$ ${\displaystyle \mathbf {R} ^{3}}$ ${\displaystyle \psi (x,y,z)-ct=0}$ ${\displaystyle \psi }$ $${\displaystyle \psi _{x}^{2}+\psi _{y}^{2}+\psi _{z}^{2}=\varepsilon \mu =n^{2},}$$ ${\displaystyle n}$

Un ejemplo de dicha superficie de discontinuidad es el frente de onda inicial que emana de una fuente que empieza a irradiar en un determinado instante de tiempo.

Las superficies de discontinuidad de campo se convierten así en frentes de onda de óptica geométrica con los campos de óptica geométrica correspondientes definidos como: $${\displaystyle {\begin{aligned}\mathbf {E} ^{*}(x,y,z)&=\mathbf {E} (x,y,z,\psi (x,y,z)/c)\\[1ex]\mathbf {H} ^{*}(x,y,z)&=\mathbf {H} (x,y,z,\psi (x,y,z)/c)\end{aligned}}}$$

Estos campos obedecen a ecuaciones de transporte consistentes con las ecuaciones de transporte del enfoque de Sommerfeld-Runge. Los rayos de luz en la teoría de Luneburg se definen como trayectorias ortogonales a las superficies de discontinuidad y se puede demostrar que obedecen al principio de Fermat del tiempo mínimo, estableciendo así la identidad de esos rayos con los rayos de luz de la óptica estándar.

Los desarrollos anteriores pueden generalizarse a medios anisotrópicos. ^[11]

La demostración del teorema de Luneburg se basa en la investigación de cómo las ecuaciones de Maxwell gobiernan la propagación de discontinuidades de soluciones. El lema técnico básico es el siguiente:

Un lema técnico. Sea una hipersuperficie (una variedad tridimensional) en el espacio-tiempo en la que uno o más de: , , , , tienen una discontinuidad finita. Entonces, en cada punto de la hipersuperficie se cumplen las siguientes fórmulas: donde el operador actúa en el -espacio (para cada ) fijo y los corchetes denotan la diferencia de valores en ambos lados de la superficie de discontinuidad (configurada de acuerdo con una convención arbitraria pero fija, p. ej., el gradiente apunta en la dirección de las cantidades que se restan de ). ${\displaystyle \varphi (x,y,z,t)=0}$ ${\displaystyle \mathbf {R} ^{4}}$ ${\displaystyle \mathbf {E} (x,y,z,t)}$ ${\displaystyle \mathbf {H} (x,y,z,t)}$ ${\displaystyle \varepsilon (x,y,z)}$ ${\displaystyle \mu (x,y,z)}$ $${\displaystyle {\begin{aligned}\nabla \varphi \cdot [\varepsilon \mathbf {E} ]&=0\\[1ex]\nabla \varphi \cdot [\mu \mathbf {H} ]&=0\\[1ex]\nabla \varphi \times [\mathbf {E} ]+{\frac {1}{c}}\,\varphi _{t}\,[\mu \mathbf {H} ]&=0\\[1ex]\nabla \varphi \times [\mathbf {H} ]-{\frac {1}{c}}\,\varphi _{t}\,[\varepsilon \mathbf {E} ]&=0\end{aligned}}}$$ ${\displaystyle \nabla }$ ${\displaystyle xyz}$ ${\displaystyle t}$ ${\displaystyle \nabla \varphi }$

Esquema de la prueba. Empecemos con las ecuaciones de Maxwell alejadas de las fuentes (unidades gaussianas): $${\displaystyle {\begin{aligned}\nabla \cdot \varepsilon \mathbf {E} =0\\[1ex]\nabla \cdot \mu \mathbf {H} =0\\[1ex]\nabla \times \mathbf {E} +{\tfrac {\mu }{c}}\,\mathbf {H} _{t}=0\\[1ex]\nabla \times \mathbf {H} -{\tfrac {\varepsilon }{c}}\,\mathbf {E} _{t}=0\end{aligned}}}$$

Utilizando el teorema de Stokes en se puede concluir de la primera de las ecuaciones anteriores que para cualquier dominio en con un límite liso por partes (tridimensional) se cumple lo siguiente: donde es la proyección de la normal unitaria exterior de sobre la porción 3D , y es la forma 3 del volumen en . De manera similar, se establece lo siguiente a partir de las ecuaciones de Maxwell restantes: ${\displaystyle \mathbf {R} ^{4}}$ ${\displaystyle D}$ ${\displaystyle \mathbf {R} ^{4}}$ ${\displaystyle \Gamma }$ $${\displaystyle \oint _{\Gamma }(\mathbf {M} \cdot \varepsilon \mathbf {E} )\,dS=0}$$ ${\displaystyle \mathbf {M} =(x_{N},y_{N},z_{N})}$ ${\displaystyle (x_{N},y_{N},z_{N},t_{N})}$ ${\displaystyle \Gamma }$ ${\displaystyle t={\rm {const}}}$ ${\displaystyle dS}$ ${\displaystyle \Gamma }$ $${\displaystyle {\begin{aligned}\oint _{\Gamma }\left(\mathbf {M} \cdot \mu \mathbf {H} \right)dS&=0\\[1.55ex]\oint _{\Gamma }\left(\mathbf {M} \times \mathbf {E} +{\frac {\mu }{c}}\,t_{N}\,\mathbf {H} \right)dS&=0\\[1.55ex]\oint _{\Gamma }\left(\mathbf {M} \times \mathbf {H} -{\frac {\varepsilon }{c}}\,t_{N}\,\mathbf {E} \right)dS&=0\end{aligned}}}$$

Ahora bien, al considerar subsuperficies arbitrarias pequeñas de y establecer pequeños vecindarios que rodeen a , y restar las integrales anteriores en consecuencia, se obtiene: donde denota el gradiente en el espacio 4D. Y como es arbitrario, los integrandos deben ser iguales a 0, lo que demuestra el lema. ${\displaystyle \Gamma _{0}}$ ${\displaystyle \Gamma }$ ${\displaystyle \Gamma _{0}}$ ${\displaystyle \mathbf {R} ^{4}}$ $${\displaystyle {\begin{aligned}\int _{\Gamma _{0}}(\nabla \varphi \cdot [\varepsilon \mathbf {E} ])\,{dS \over \|\nabla ^{4D}\varphi \|}&=0\\[1ex]\int _{\Gamma _{0}}(\nabla \varphi \cdot [\mu \mathbf {H} ])\,{dS \over \|\nabla ^{4D}\varphi \|}&=0\\[1ex]\int _{\Gamma _{0}}\left(\nabla \varphi \times [\mathbf {E} ]+{1 \over c}\,\varphi _{t}\,[\mu \mathbf {H} ]\right)\,{\frac {dS}{\|\nabla ^{4D}\varphi \|}}&=0\\[1ex]\int _{\Gamma _{0}}\left(\nabla \varphi \times [\mathbf {H} ]-{1 \over c}\,\varphi _{t}\,[\varepsilon \mathbf {E} ]\right)\,{\frac {dS}{\|\nabla ^{4D}\varphi \|}}&=0\end{aligned}}}$$ ${\displaystyle \nabla ^{4D}}$ ${\displaystyle xyzt}$ ${\displaystyle \Gamma _{0}}$

Ahora es fácil demostrar que, a medida que se propagan a través de un medio continuo, las superficies de discontinuidad obedecen a la ecuación eikonal. En concreto, si y son continuas, entonces las discontinuidades de y satisfacen: y . En este caso, las dos últimas ecuaciones del lema se pueden escribir como: ${\displaystyle \varepsilon }$ ${\displaystyle \mu }$ ${\displaystyle \mathbf {E} }$ ${\displaystyle \mathbf {H} }$ ${\displaystyle [\varepsilon \mathbf {E} ]=\varepsilon [\mathbf {E} ]}$ ${\displaystyle [\mu \mathbf {H} ]=\mu [\mathbf {H} ]}$

$${\displaystyle {\begin{aligned}\nabla \varphi \times [\mathbf {E} ]+{\mu \over c}\,\varphi _{t}\,[\mathbf {H} ]&=0\\[1ex]\nabla \varphi \times [\mathbf {H} ]-{\varepsilon \over c}\,\varphi _{t}\,[\mathbf {E} ]&=0\end{aligned}}}$$

Tomando el producto vectorial de la segunda ecuación por y sustituyendo la primera se obtiene: ${\displaystyle \nabla \varphi }$ $${\displaystyle \nabla \varphi \times (\nabla \varphi \times [\mathbf {H} ])-{\varepsilon \over c}\,\varphi _{t}\,(\nabla \varphi \times [\mathbf {E} ])=(\nabla \varphi \cdot [\mathbf {H} ])\,\nabla \varphi -\|\nabla \varphi \|^{2}\,[\mathbf {H} ]+{\varepsilon \mu \over c^{2}}\varphi _{t}^{2}\,[\mathbf {H} ]=0}$$

La continuidad de y la segunda ecuación del lema implican: , por lo tanto, para puntos que se encuentran únicamente en la superficie : ${\displaystyle \mu }$ ${\displaystyle \nabla \varphi \cdot [\mathbf {H} ]=0}$ ${\displaystyle \varphi =0}$ $${\displaystyle \|\nabla \varphi \|^{2}={\varepsilon \mu \over c^{2}}\varphi _{t}^{2}}$$

(Tenga en cuenta que la presencia de la discontinuidad es esencial en este paso, ya que de lo contrario estaríamos dividiendo por cero).

Debido a las consideraciones físicas, se puede suponer sin pérdida de generalidad que tiene la siguiente forma: , es decir, una superficie 2D que se mueve a través del espacio, modelada como superficies de nivel de . ( Existe matemáticamente si por el teorema de función implícita .) La ecuación anterior escrita en términos de se convierte en: es decir, que es la ecuación eikonal y se cumple para todos , , , ya que la variable está ausente. Otras leyes de la óptica como la ley de Snell y las fórmulas de Fresnel se pueden obtener de manera similar considerando discontinuidades en y . ${\displaystyle \varphi }$ ${\displaystyle \varphi (x,y,z,t)=\psi (x,y,z)-ct}$ ${\displaystyle \psi }$ ${\displaystyle \psi }$ ${\displaystyle \varphi _{t}\neq 0}$ ${\displaystyle \psi }$ $${\displaystyle \|\nabla \psi \|^{2}={\varepsilon \mu \over c^{2}}\,(-c)^{2}=\varepsilon \mu =n^{2}}$$ $${\displaystyle \psi _{x}^{2}+\psi _{y}^{2}+\psi _{z}^{2}=n^{2}}$$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$ ${\displaystyle t}$ ${\displaystyle \varepsilon }$ ${\displaystyle \mu }$

Ecuación general utilizando notación de cuatro vectores

En la notación de cuatro vectores utilizada en la relatividad especial , la ecuación de onda se puede escribir como $${\displaystyle {\frac {\partial ^{2}\psi }{\partial x_{i}\partial x^{i}}}=0}$$

y la sustitución conduce a ^[12] ${\displaystyle \psi =Ae^{iS/\varepsilon }}$ $${\displaystyle -{\frac {A}{\varepsilon ^{2}}}{\frac {\partial S}{\partial x_{i}}}{\frac {\partial S}{\partial x^{i}}}+{\frac {2i}{\varepsilon }}{\frac {\partial A}{\partial x_{i}}}{\frac {\partial S}{\partial x^{i}}}+{\frac {iA}{\varepsilon }}{\frac {\partial ^{2}S}{\partial x_{i}\partial x^{i}}}+{\frac {\partial ^{2}A}{\partial x_{i}\partial x^{i}}}=0.}$$

Por lo tanto, la ecuación eikonal viene dada por $${\displaystyle {\frac {\partial S}{\partial x_{i}}}{\frac {\partial S}{\partial x^{i}}}=0.}$$

Una vez que se encuentra eikonal resolviendo la ecuación anterior, el cuatro-vector de onda se puede encontrar a partir de $${\displaystyle k_{i}=-{\frac {\partial S}{\partial x^{i}}}.}$$

Véase también

• Óptica hamiltoniana
• Acústica geométrica

Referencias

1. Arthur Schuster , Introducción a la teoría de la óptica , Londres: Edward Arnold, 1904 en línea.
2. Greivenkamp, ​​John E. (2004). Guía de campo de óptica geométrica . Guías de campo SPIE. vol. 1. ESPÍA . págs. 19-20. ISBN 0-8194-5294-7.
3. Hugh D. Young (1992). Física universitaria 8.ª edición . Addison-Wesley. ISBN 0-201-52981-5.Capítulo 35.
4. EW Marchand, Gradient Index Optics, Nueva York, NY, Academic Press, 1978.
5. Hecht, Eugene (1987). Óptica (2.ª ed.). Addison Wesley. ISBN 0-201-11609-X.Capítulos 5 y 6.
6. Sommerfeld, A. y Runge, J. (1911). Anwendung der Vektorrechnung auf die Grundlagen der geometrischen Optik. Annalen der Physik, 340(7), 277-298.
7. Born, M., y Wolf, E. (2013). Principios de óptica: teoría electromagnética de propagación, interferencia y difracción de la luz . Elsevier.
8. Sommerfield, A.; J., Runge. "La aplicación del cálculo vectorial a los fundamentos de la óptica geométrica" ​​(PDF) . Física neoclásica . Traducido por DH Delphenich . Consultado el 3 de noviembre de 2023 .
9. Borowitz, S. (1967). Fundamentos de mecánica cuántica, partículas, ondas y mecánica ondulatoria.
10. Luneburg, RK, Teoría matemática de la óptica , Brown University Press 1944 [notas mimeografiadas], University of California Press 1964
11. Kline, M., Kay, IW, Teoría electromagnética y óptica geométrica , Interscience Publishers 1965
12. Landau, LD y Lifshitz, EM (1975). La teoría clásica de campos.

Lectura adicional

• Robert Alfred Herman (1900) Un tratado sobre óptica geométrica de Archive.org .
• "La luz de los ojos y el paisaje iluminado de la visión" es un manuscrito, en árabe, sobre óptica geométrica, que data del siglo XVI.
• Teoría de sistemas de rayos – WR Hamilton en Transactions of the Royal Irish Academy , Vol. XV, 1828.

Traducciones al inglés de algunos libros y artículos antiguos

• H. Bruns, "El eikonal"
• M. Malus, "Optica"
• J. Plucker, "Discusión de la forma general de las ondas de luz"
• E. Kummer, "Teoría general de los sistemas de rayos rectilíneos"
• E. Kummer, presentación sobre sistemas de rayos rectilíneos realizables ópticamente
• R. Meibauer, "Teoría de sistemas rectilíneos de rayos de luz"
• M. Pasch, "Sobre las superficies focales de los sistemas de rayos y las superficies de singularidad de los complejos"
• A. Levistal, "Investigación en óptica geométrica"
• F. Klein, "Sobre el Bruns eikonal"
• R. Dontot, "Sobre invariantes integrales y algunos puntos de óptica geométrica"
• T. de Donder, "Sobre los invariantes integrales de la óptica"

Enlaces externos

• Conferencia de Feynman sobre Óptica Geométrica