IEEE 754

Estándar IEEE para aritmética de punto flotante

El estándar IEEE para aritmética de punto flotante ( IEEE 754 ) es un estándar técnico para la aritmética de punto flotante establecido originalmente en 1985 por el Instituto de Ingenieros Eléctricos y Electrónicos (IEEE). El estándar abordó muchos problemas encontrados en las diversas implementaciones de punto flotante que dificultaban su uso de manera confiable y portátil . Muchas unidades de punto flotante de hardware utilizan el estándar IEEE 754.

La norma define:

• Formatos aritméticos: conjuntos de datos binarios y decimales de punto flotante, que consisten en números finitos (incluidos ceros con signo y números subnormales ), infinitos y valores especiales "que no son números" ( NaN )
• formatos de intercambio: codificaciones (cadenas de bits) que pueden utilizarse para intercambiar datos de punto flotante de forma eficiente y compacta
• Reglas de redondeo: propiedades que deben cumplirse al redondear números durante operaciones aritméticas y conversiones.
• Operaciones: operaciones aritméticas y otras operaciones (como funciones trigonométricas ) en formatos aritméticos.
• manejo de excepciones: indicaciones de condiciones excepcionales (como división por cero , desbordamiento, etc.)

IEEE 754-2008 , publicado en agosto de 2008, incluye casi la totalidad del estándar IEEE 754-1985 original , además del estándar IEEE 854-1987 para aritmética de punto flotante independiente de la base . La versión actual, IEEE 754-2019, se publicó en julio de 2019. ^[1] Es una revisión menor de la versión anterior, que incorpora principalmente aclaraciones, correcciones de defectos y nuevas operaciones recomendadas.

Historia

La necesidad de un estándar de punto flotante surgió del caos en la industria de la computación científica y empresarial en los años 1960 y 1970. IBM utilizó un formato de punto flotante hexadecimal con un significado más largo y un exponente más corto ^{[ aclaración necesaria ]} . Las computadoras CDC y Cray utilizaron la representación del complemento a uno , que admite un valor de +0 y −0. Las computadoras CDC de 60 bits no tenían sumadores completos de 60 bits, por lo que la aritmética de números enteros estaba limitada a 48 bits de precisión de la unidad de punto flotante. El procesamiento de excepciones de división por cero era diferente en diferentes computadoras. Mover datos entre sistemas e incluso repetir los mismos cálculos en diferentes sistemas era a menudo difícil.

El primer estándar IEEE para aritmética de punto flotante, IEEE 754-1985 , se publicó en 1985. Cubría únicamente la aritmética binaria de punto flotante.

En agosto de 2008 se publicó una nueva versión, IEEE 754-2008 , tras un proceso de revisión de siete años, presidido por Dan Zuras y editado por Mike Cowlishaw . Reemplazó tanto a IEEE 754-1985 (aritmética binaria de punto flotante) como a IEEE 854-1987 Standard for Radix-Independent Floating-Point Arithmetic . Los formatos binarios del estándar original se incluyen en este nuevo estándar junto con tres nuevos formatos básicos, uno binario y dos decimales. Para cumplir con el estándar actual, una implementación debe implementar al menos uno de los formatos básicos como formato aritmético y como formato de intercambio.

La norma internacional ISO/IEC/IEEE 60559:2011 (con contenido idéntico al IEEE 754-2008) ha sido aprobada para su adopción a través de ISO / IEC JTC 1 /SC 25 bajo el Acuerdo ISO/IEEE PSDO ^{[2] [3]} y publicada. ^[4]

La versión actual, IEEE 754-2019 publicada en julio de 2019, se deriva de IEEE 754-2008 y la reemplaza, luego de un proceso de revisión iniciado en septiembre de 2015, presidido por David G. Hough y editado por Mike Cowlishaw. Incorpora principalmente aclaraciones (por ejemplo, totalOrder ) y correcciones de defectos (por ejemplo, minNum ), pero también incluye algunas nuevas operaciones recomendadas (por ejemplo, augmentedAddition ). ^{[5] [6]}

La norma internacional ISO/IEC 60559:2020 (con contenido idéntico al IEEE 754-2019) ha sido aprobada para su adopción a través de ISO/IEC JTC 1 /SC 25 y publicada. ^[7]

La próxima revisión prevista de la norma será en 2029. ^[8]

Formatos

Un formato IEEE 754 es un "conjunto de representaciones de valores numéricos y símbolos". Un formato también puede incluir cómo se codifica el conjunto. ^[9]

Un formato de punto flotante se especifica mediante

• una base (también llamada radix ) b , que es 2 (binario) o 10 (decimal) en IEEE 754;
• una precisión p ;
• un rango de exponentes de emin a emax , con emin = 1 − emax , o equivalentemente emin = − ( emax − 1), para todos los formatos IEEE 754.

Un formato comprende

• Números finitos, que pueden describirse mediante tres enteros: s  = un signo (cero o uno), c  = un mantisa (o coeficiente ) que no tiene más de p dígitos cuando se escribe en base b (es decir, un entero en el rango de 0 a b ^p  − 1), y q  = un exponente tal que emin ≤ q  +  p  − 1 ≤ emax . El valor numérico de un número finito de este tipo es (−1) ^s × c × b ^q . ^[a] Además, hay dos valores cero, llamados ceros con signo : el bit de signo especifica si un cero es +0 (cero positivo) o −0 (cero negativo).
• Dos infinitos: +∞ y −∞.
• Dos tipos de NaN (no un número): un NaN silencioso (qNaN) y un NaN de señalización (sNaN).

Por ejemplo, si b = 10, p = 7 y emax = 96, entonces emin = −95, el mantisa satisface 0 ≤ c ≤9 999 999 , y el exponente satisface −101 ≤ q ≤ 90 . En consecuencia, el número positivo distinto de cero más pequeño que se puede representar es 1×10 ⁻¹⁰¹ , y el más grande es 9999999×10 ⁹⁰ (9,999999×10 ⁹⁶ ), por lo que el rango completo de números es −9,999999×10 ⁹⁶ hasta 9,999999×10 ⁹⁶ . Los números − b ^{1− emax} y b ^{1− emax} (aquí, −1×10 ⁻⁹⁵ y 1×10 ^{−95 ) son los} números normales más pequeños (en magnitud) ; los números distintos de cero entre estos números más pequeños se denominan números subnormales .

Representación y codificación en la memoria

Algunos números pueden tener varias representaciones posibles en coma flotante. Por ejemplo, si b  = 10 y p  = 7, entonces −12,345 se puede representar mediante −12345×10 ⁻³ , −123450×10 ⁻⁴ y −1234500×10 ⁻⁵ . Sin embargo, para la mayoría de las operaciones, como las operaciones aritméticas, el resultado (valor) no depende de la representación de las entradas.

Para los formatos decimales, cualquier representación es válida y el conjunto de estas representaciones se denomina cohorte . Cuando un resultado puede tener varias representaciones, el estándar especifica qué miembro de la cohorte se elige.

Para los formatos binarios, la representación se hace única al elegir el exponente representable más pequeño que permita que el valor se represente exactamente. Además, el exponente no se representa directamente, sino que se agrega un sesgo para que el exponente representable más pequeño se represente como 1, y se usa 0 para números subnormales. Para los números con un exponente en el rango normal (el campo del exponente no es todo unos ni todo ceros), el bit inicial del mantis siempre será 1. En consecuencia, un 1 inicial puede estar implícito en lugar de estar presente explícitamente en la codificación de memoria, y bajo el estándar la parte representada explícitamente del mantis estará entre 0 y 1. Esta regla se llama convención de bits iniciales , convención de bits implícita o convención de bits ocultos . Esta regla permite que el formato binario tenga un bit adicional de precisión. La convención de bits iniciales no se puede usar para los números subnormales ya que tienen un exponente fuera del rango de exponentes normales y se escala por el exponente representado más pequeño como se usa para los números normales más pequeños.

Debido a la posibilidad de múltiples codificaciones (al menos en formatos llamados formatos de intercambio ), un NaN puede llevar otra información: un bit de signo (que no tiene significado, pero puede ser utilizado por algunas operaciones) y una carga útil , que está destinada a información de diagnóstico que indica la fuente del NaN (pero la carga útil puede tener otros usos, como el NaN-boxing ^{[10] [11] [12]} ).

Formatos básicos y de intercambio

El estándar define cinco formatos básicos que reciben su nombre por su base numérica y la cantidad de bits utilizados en su codificación de intercambio. Hay tres formatos básicos binarios de punto flotante (codificados con 32, 64 o 128 bits) y dos formatos básicos decimales de punto flotante (codificados con 64 o 128 bits). Los formatos binary32 y binary64 son los formatos simple y doble de IEEE 754-1985 respectivamente. Una implementación conforme debe implementar completamente al menos uno de los formatos básicos.

El estándar también define formatos de intercambio , que generalizan estos formatos básicos. ^[13] Para los formatos binarios, se requiere la convención de bits inicial. La siguiente tabla resume algunos de los posibles formatos de intercambio (incluidos los formatos básicos).

En la tabla anterior, los valores enteros son exactos, mientras que los valores en notación decimal (por ejemplo, 1.0) son valores redondeados. Los exponentes mínimos que se enumeran son para números normales; la representación especial de números subnormales permite representar números incluso más pequeños (en magnitud) con cierta pérdida de precisión. Por ejemplo, el número positivo más pequeño que se puede representar en binario64 es 2 ⁻¹⁰⁷⁴ ; las contribuciones a la cifra −1074 incluyen el valor emin −1022 y todos menos uno de los 53 bits de mantisa (2 ^{−1022 − (53 − 1)}  = 2 ⁻¹⁰⁷⁴ ).

Los dígitos decimales son la precisión del formato expresado en términos de un número equivalente de dígitos decimales. Se calcula como dígitos × log ₁₀ base . Por ejemplo, el binario 128 tiene aproximadamente la misma precisión que un número decimal de 34 dígitos.

log ₁₀  MAXVAL es una medida del rango de la codificación. Su parte entera es el exponente más grande que se muestra en la salida de un valor en notación científica con un dígito inicial en la mantisa antes del punto decimal (por ejemplo, 1,698·10 ³⁸ está cerca del valor más grande en binary32, 9,999999·10 ⁹⁶ es el valor más grande en decimal32).

Los formatos binary32 (simple) y binary64 (doble) son dos de los formatos más comunes que se utilizan en la actualidad. La siguiente figura muestra la precisión absoluta de ambos formatos en un rango de valores. Esta figura se puede utilizar para seleccionar un formato adecuado según el valor esperado de un número y la precisión requerida.

Precisión de binary32 y binary64 en el rango de 10 ⁻¹² a 10 ¹²

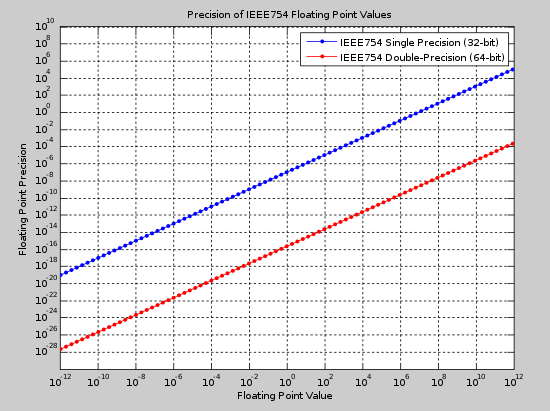
Un ejemplo de diseño para punto flotante de 32 bits es

y el diseño de 64 bits es similar.

Formatos de precisión ampliados y extensibles

El estándar especifica formatos de precisión ampliados y extensibles opcionales , que proporcionan una mayor precisión que los formatos básicos. ^[14] Un formato de precisión ampliado amplía un formato básico utilizando más precisión y un mayor rango de exponentes. Un formato de precisión ampliable permite al usuario especificar la precisión y el rango de exponentes. Una implementación puede utilizar cualquier representación interna que elija para dichos formatos; todo lo que necesita definirse son sus parámetros ( b , p y emax ). Estos parámetros describen de forma única el conjunto de números finitos (combinaciones de signo, mantisa y exponente para la base dada) que puede representar.

El estándar recomienda que los estándares de lenguaje proporcionen un método para especificar p y emax para cada base b admitida . ^[15] El estándar recomienda que los estándares de lenguaje y las implementaciones admitan un formato extendido que tenga una precisión mayor que el formato básico más grande admitido para cada base b . ^[16] Para un formato extendido con una precisión entre dos formatos básicos, el rango de exponentes debe ser tan grande como el del siguiente formato básico más amplio. Por ejemplo, un número binario de precisión extendida de 64 bits debe tener un 'emax' de al menos 16383. El formato extendido x87 de 80 bits cumple con este requisito.

El estándar IEEE 754-1985 original también tenía el concepto de formatos extendidos , pero sin ninguna relación obligatoria entre emin y emax . Por ejemplo, el formato de 80 bits Motorola 68881 , ^[17] donde emin = − emax , era un formato extendido conforme, pero dejó de cumplir las normas en la revisión de 2008.

Formatos de intercambio

Los formatos de intercambio están destinados al intercambio de datos de punto flotante utilizando una cadena de bits de longitud fija para un formato determinado.

Binario

Para el intercambio de números binarios en coma flotante se definen formatos de intercambio de longitud 16 bits, 32 bits, 64 bits y cualquier múltiplo de 32 bits ≥ 128 ^[e] . El formato de 16 bits está destinado al intercambio o almacenamiento de números pequeños (por ejemplo, para gráficos).

El esquema de codificación para estos formatos de intercambio binario es el mismo que el de IEEE 754-1985: un bit de signo, seguido de w bits de exponente que describen el exponente desplazado por un sesgo , y p  − 1 bits que describen la mantisa. El ancho del campo de exponente para un formato de k bits se calcula como w  = round(4 log ₂ ( k )) − 13. Los formatos existentes de 64 y 128 bits siguen esta regla, pero los formatos de 16 y 32 bits tienen más bits de exponente (5 y 8 respectivamente) de los que proporcionaría esta fórmula (3 y 7 respectivamente).

Al igual que con IEEE 754-1985, el campo de exponente sesgado se llena con todos los bits 1 para indicar infinito (campo de significando final = 0) o un NaN (campo de significando final ≠ 0). Para los NaN, los NaN silenciosos y los NaN de señalización se distinguen utilizando exclusivamente el bit más significativo del campo de significando final, ^[f] y la carga útil se transporta en los bits restantes.

Decimal

Para el intercambio de números decimales en coma flotante, se definen formatos de intercambio de cualquier múltiplo de 32 bits. Al igual que con el intercambio binario, el esquema de codificación para los formatos de intercambio decimal codifica el signo, el exponente y la mantisa. Se definen dos codificaciones diferentes a nivel de bits y el intercambio se complica por el hecho de que puede requerirse algún indicador externo de la codificación en uso.

Las dos opciones permiten codificar el mantisa como una secuencia comprimida de dígitos decimales utilizando decimales densamente empaquetados o, alternativamente, como un entero binario . La primera opción es más conveniente para la implementación directa del hardware del estándar, mientras que la segunda es más adecuada para la emulación de software en una computadora binaria. En cualquier caso, el conjunto de números (combinaciones de signo, mantisa y exponente) que se puede codificar es idéntico, y los valores especiales (±cero con el exponente mínimo, ±infinito, NaN silenciosos y NaN de señalización) tienen codificaciones idénticas.

Reglas de redondeo

La norma define cinco reglas de redondeo. Las dos primeras reglas redondean al valor más próximo; las demás se denominan redondeos dirigidos :

Redondeos al más cercano

• Redondear al más cercano, empates al par  : redondea al valor más cercano; si el número está a la mitad, se redondea al valor más cercano con un dígito par menos significativo.
• Redondear al más cercano, empata lejos de cero (o empata lejos ): redondea al valor más cercano; si el número está a la mitad, se redondea al valor más cercano superior (para números positivos) o inferior (para números negativos).

En los extremos, un valor con una magnitud estrictamente menor que se redondeará al número finito mínimo o máximo (dependiendo del signo del valor). Cualquier número con exactamente esta magnitud se considera un empate; esta elección de empate puede conceptualizarse como el punto medio entre y , que, si el exponente no estuviera limitado, sería el siguiente número de punto flotante representable de mayor magnitud. Los números con una magnitud estrictamente mayor que k se redondean al infinito correspondiente. ^[18] ${\displaystyle k=b^{\text{emax}}\left(b-{\tfrac {1}{2}}b^{1-p}\right)}$ ${\displaystyle \pm b^{\text{emax}}(b-b^{1-p})}$ ${\displaystyle \pm b^{{\text{emax}}+1}}$

"Redondear al más cercano, igual al par" es el valor predeterminado para el punto flotante binario y el valor predeterminado recomendado para el decimal. "Redondear al más cercano, igual al más lejano" solo es necesario para las implementaciones decimales. ^[19]

Redondeos dirigidos

• Redondeo hacia 0  : redondeo dirigido hacia cero (también conocido como truncamiento ).
• Redondear hacia +∞  – redondeo dirigido hacia el infinito positivo (también conocido como redondeo hacia arriba o techo ).
• Redondear hacia −∞  – redondeo dirigido hacia el infinito negativo (también conocido como redondeo hacia abajo o piso ).

A menos que se especifique lo contrario, el resultado en coma flotante de una operación se determina aplicando la función de redondeo al resultado (matemático) infinitamente preciso. Se dice que una operación de este tipo está correctamente redondeada . Este requisito se denomina redondeo correcto . ^[20]

Operaciones requeridas

Las operaciones necesarias para un formato aritmético compatible (incluidos los formatos básicos) incluyen:

• Conversiones a y desde números enteros ^{[21] [22]}
• Valores consecutivos anteriores y siguientes ^[21]
• Operaciones aritméticas (suma, resta, multiplicación, división, raíz cuadrada, multiplicación-suma fusionada , resto, mínimo, máximo) ^{[21] [22]}
• Conversiones (entre formatos, hacia y desde cadenas, etc.) ^{[23] [24]}
• Escalado y cuantificación (para decimales) ^{[25] [26]}
• Copiar y manipular el signo (abs, negar, etc.) ^[27]
• Comparaciones y ordenamiento total ^{[28] [29]}
• Clasificación de números (subnormales, finitos, etc.) y prueba de NaN ^[30]
• Prueba y configuración de indicadores de estado ^[31]

Predicados de comparación

El estándar proporciona predicados de comparación para comparar un dato de punto flotante con otro en el formato aritmético admitido. ^[32] Cualquier comparación con un NaN se trata como desordenada. −0 y +0 se comparan como iguales.

Predicado de ordenación total

El estándar proporciona un predicado totalOrder , que define un ordenamiento total de los miembros canónicos del formato aritmético admitido. ^[33] El predicado concuerda con los predicados de comparación (véase la sección § Predicados de comparación) cuando un número de punto flotante es menor que el otro. Las principales diferencias son: ^[34]

• NaN es ordenable.
  • NaN se trata como si tuviera un valor absoluto mayor que Infinity (o cualquier otro número de punto flotante). (−NaN < −Infinity; +Infinity < +NaN).
  • qNaN y sNaN se tratan como si qNaN tuviera un valor absoluto mayor que sNaN. (−qNaN < −sNaN; +sNaN < +qNaN.)
  • Luego, el NaN se ordena según la carga útil. En IEEE 754-2008, un NaN con una carga útil menor se considera que tiene un valor absoluto menor. En IEEE 754-2019, se acepta cualquier orden definido por la implementación.
• El cero negativo se trata como más pequeño que el cero positivo.
• Si ambos lados de la comparación se refieren al mismo dato de punto flotante, el que tiene el exponente menor se trata como si tuviera un valor absoluto menor. ^[33]

El predicado totalOrder no impone un orden total a todas las codificaciones de un formato. En particular, no distingue entre diferentes codificaciones de la misma representación de punto flotante, como cuando una o ambas codificaciones no son canónicas. ^[33] IEEE 754-2019 incorpora aclaraciones de totalOrder .

Para los formatos de intercambio binario cuya codificación sigue la recomendación IEEE 754-2008 sobre la ubicación del bit de señalización NaN , la comparación es idéntica a una que convierte los números de punto flotante en un entero de signo-magnitud (asumiendo un orden de carga útil consistente con esta comparación), un viejo truco para la comparación de FP sin una FPU. ^[35]

Manejo de excepciones

El estándar define cinco excepciones, cada una de las cuales devuelve un valor predeterminado y tiene un indicador de estado correspondiente que se activa cuando se produce la excepción. ^[g] No se requiere ningún otro manejo de excepciones, pero se recomiendan alternativas adicionales no predeterminadas (consulte § Manejo de excepciones alternativo).

Las cinco posibles excepciones son

• Operación no válida: matemáticamente no definida, p. ej., la raíz cuadrada de un número negativo. De forma predeterminada, devuelve qNaN.
• División por cero: una operación sobre operandos finitos da un resultado infinito exacto, p. ej., 1/0 o log(0). De forma predeterminada, devuelve ±infinito.
• Desbordamiento: un resultado finito es demasiado grande para ser representado con precisión (es decir, su exponente con un rango de exponentes ilimitado sería mayor que emax ). De manera predeterminada, devuelve ±infinito para los modos de redondeo al más cercano (y sigue las reglas de redondeo para los modos de redondeo dirigido).
• Desbordamiento por defecto: un resultado es muy pequeño (fuera del rango normal). De manera predeterminada, devuelve un número menor o igual al número normal positivo mínimo en magnitud (siguiendo las reglas de redondeo); un número por debajo de lo normal siempre implica una excepción de desbordamiento por defecto, pero de manera predeterminada, si es exacto, no se activa ninguna alarma.
• Inexacto: el resultado exacto (es decir, no redondeado) no se puede representar con exactitud. De forma predeterminada, devuelve el resultado redondeado correctamente.

Estas son las mismas cinco excepciones que se definieron en IEEE 754-1985, pero la excepción de división por cero se ha extendido a operaciones distintas de la división.

Algunas implementaciones de punto flotante decimal definen excepciones adicionales, ^{[36] [37]} que no son parte de IEEE 754:

• Limitado: el exponente de un resultado es demasiado grande para el formato de destino. De forma predeterminada, se agregarán ceros finales al coeficiente para reducir el exponente al valor más grande que se pueda utilizar. Si esto no es posible (porque esto provocaría que la cantidad de dígitos necesarios sea mayor que el formato de destino), se produce una excepción de desbordamiento.
• Redondeado: el coeficiente de un resultado requiere más dígitos que los que proporciona el formato de destino. Se indica una excepción inexacta si se descartan dígitos distintos de cero.

Además, operaciones como cuantificar cuando alguno de los operandos es infinito o cuando el resultado no se ajusta al formato de destino también indicarán una excepción de operación no válida. ^[38]

Valores especiales

Cero firmado

En el estándar IEEE 754, el cero tiene signo, lo que significa que existe tanto un "cero positivo" (+0) como un "cero negativo" (−0). En la mayoría de los entornos de ejecución , el cero positivo suele imprimirse como " 0" y el cero negativo como " -0". Los dos valores se comportan como iguales en las comparaciones numéricas, pero algunas operaciones devuelven resultados diferentes para +0 y −0. Por ejemplo, 1/(−0) devuelve infinito negativo, mientras que 1/(+0) devuelve infinito positivo (de modo que se mantiene la identidad 1/(1/±∞) = ±∞ ). Otras funciones comunes con una discontinuidad en x = 0 que podrían tratar a +0 y −0 de forma diferente incluyen Γ ( x ) y la raíz cuadrada principal de y + xi para cualquier número negativo y . Al igual que con cualquier esquema de aproximación, las operaciones que involucran "cero negativo" ocasionalmente pueden causar confusión. Por ejemplo, en IEEE 754, x = y no siempre implica 1/ x = 1/ y , ya que 0 = −0 pero 1/0 ≠ 1/(−0) . ^[39] Además, para la raíz cuadrada recíproca, rSqrt(±0) es ±∞ mientras que la función matemática sobre los números reales no tiene ningún valor negativo. ${\displaystyle 1{\big /}{\sqrt {x{\vphantom {t}}}}}$

Números subnormales

Los valores subnormales llenan el espacio de desbordamiento con valores en los que la distancia absoluta entre ellos es la misma que la de los valores adyacentes que se encuentran justo fuera del espacio de desbordamiento. Esto supone una mejora con respecto a la práctica anterior de tener solo cero en el espacio de desbordamiento y donde los resultados de desbordamiento se reemplazaban por cero (se alineaban con cero). ^[40]

El hardware de punto flotante moderno generalmente maneja valores subnormales (así como valores normales) y no requiere emulación de software para valores subnormales.

Infinitos

Los infinitos de la línea de números reales extendida se pueden representar en tipos de datos de punto flotante IEEE, al igual que los valores de punto flotante ordinarios como 1, 1,5, etc. No son valores de error de ninguna manera, aunque a menudo se utilizan (dependiendo del redondeo) como valores de reemplazo cuando hay un desbordamiento. En una excepción de división por cero, se devuelve un infinito positivo o negativo como resultado exacto. Un infinito también se puede introducir como un numeral (como la macro "INFINITY" de C, o " ∞ " si el lenguaje de programación permite esa sintaxis).

IEEE 754 requiere que los infinitos se manejen de una manera razonable, como por ejemplo:

• (+∞) + (+7) = (+∞)
• (+∞) × (−2) = (−∞)
• (+∞) × 0 = NaN – no hay nada significativo que hacer

NaN

IEEE 754 especifica un valor especial llamado "No es un número" (NaN) que se devolverá como resultado de ciertas operaciones "no válidas", como 0/0, ∞×0 o sqrt(−1). En general, los NaN se propagarán, es decir, la mayoría de las operaciones que involucran un NaN darán como resultado un NaN, aunque las funciones que darían un resultado definido para cualquier valor de punto flotante dado también lo harán para los NaN, por ejemplo, NaN ^ 0 = 1. Hay dos tipos de NaN: los NaN silenciosos predeterminados y, opcionalmente, los NaN de señalización . Un NaN de señalización en cualquier operación aritmética (incluidas las comparaciones numéricas) hará que se señalice una excepción de "operación no válida".

La representación de los NaN especificada por el estándar tiene algunos bits no especificados que podrían utilizarse para codificar el tipo o la fuente de error; pero no existe ningún estándar para esa codificación. En teoría, un sistema en tiempo de ejecución podría utilizar la señalización de los NaN para marcar variables no inicializadas o ampliar los números de punto flotante con otros valores especiales sin ralentizar los cálculos con valores ordinarios, aunque dichas extensiones no son comunes.

Fundamento del diseño

William Kahan . Arquitecto principal del coprocesador de punto flotante Intel 80x87 y del estándar de punto flotante IEEE 754.

Es un error muy común pensar que las características más esotéricas del estándar IEEE 754 que se analizan aquí, como los formatos extendidos, NaN, los infinitos, los subnormales, etc., son de interés únicamente para los analistas numéricos o para aplicaciones numéricas avanzadas. De hecho, ocurre lo contrario: estas características están diseñadas para proporcionar valores predeterminados seguros y robustos para programadores poco sofisticados en el ámbito numérico, además de dar soporte a bibliotecas numéricas sofisticadas para expertos. El diseñador clave del IEEE 754, William Kahan , señala que es incorrecto "... [considerar] características del estándar IEEE 754 para la aritmética binaria de punto flotante que... [no] son ​​apreciadas como características que sólo pueden utilizar los expertos numéricos. Los hechos son todo lo contrario. En 1977, esas características se diseñaron en el Intel 8087 para servir al mercado más amplio posible... El análisis de errores nos dice cómo diseñar una aritmética de punto flotante, como el estándar IEEE 754, moderadamente tolerante con la ignorancia bienintencionada entre los programadores". ^[41]

• Los valores especiales como infinito y NaN garantizan que la aritmética de punto flotante sea algebraicamente completa: cada operación de punto flotante produce un resultado bien definido y no lanzará, por defecto, una interrupción o trampa de la máquina. Además, las opciones de valores especiales devueltos en casos excepcionales fueron diseñadas para dar la respuesta correcta en muchos casos. Por ejemplo, bajo la aritmética IEEE 754, las fracciones continuas como R(z) := 7 − 3/[z − 2 − 1/(z − 7 + 10/[z − 2 − 2/(z − 3)])] darán la respuesta correcta en todas las entradas, ya que la división potencial por cero, por ejemplo para z = 3 , se maneja correctamente dando +infinito, y por lo tanto, tales excepciones se pueden ignorar con seguridad. ^[42] Como señaló Kahan, la trampa no controlada consecutiva a un desbordamiento de conversión de punto flotante a entero de 16 bits que causó la pérdida de un cohete Ariane 5 no habría ocurrido bajo la política de punto flotante IEEE 754 predeterminada. ^[41]
• Los números subnormales garantizan que, para los números de punto flotante finitos x e y, x − y = 0 si y solo si x = y, como se esperaba, pero lo cual no se cumplía con las representaciones de punto flotante anteriores. ^[43]
• En cuanto a la lógica de diseño del formato x87 de 80 bits , Kahan señala: "Este formato extendido está diseñado para usarse, con una pérdida insignificante de velocidad, para todo, excepto la aritmética más simple con operandos float y double. Por ejemplo, debería usarse para variables scratch en bucles que implementan recurrencias como evaluación polinómica, productos escalares, fracciones parciales y continuas. A menudo evita desbordamientos excesivos o insuficientes prematuros o cancelaciones locales severas que pueden arruinar algoritmos simples". ^[44] El cálculo de resultados intermedios en un formato extendido con alta precisión y exponente extendido tiene precedentes en la práctica histórica del cálculo científico y en el diseño de calculadoras científicas , por ejemplo, las calculadoras financieras de Hewlett-Packard realizaban funciones aritméticas y financieras con tres decimales más significativas de las que almacenaban o mostraban. ^[44] La implementación de precisión extendida permitió que se desarrollaran fácilmente bibliotecas de funciones elementales estándar que normalmente brindaban resultados de precisión doble dentro de una unidad en el último lugar (ULP) a alta velocidad.
• El redondeo correcto de los valores al valor representable más próximo evita sesgos sistemáticos en los cálculos y retrasa el aumento de errores. El redondeo de los valores elimina el sesgo estadístico que puede producirse al sumar cifras similares.
• El redondeo dirigido fue pensado como una ayuda para verificar los límites de error, por ejemplo, en la aritmética de intervalos . También se utiliza en la implementación de algunas funciones.
• La base matemática de las operaciones, en particular el redondeo correcto, permite demostrar propiedades matemáticas y diseñar algoritmos de punto flotante como 2Sum, Fast2Sum y el algoritmo de suma de Kahan , por ejemplo, para mejorar la precisión o implementar subrutinas aritméticas de precisión múltiple con relativa facilidad.

Una propiedad de los formatos de precisión simple y doble es que su codificación permite ordenarlos fácilmente sin usar hardware de punto flotante, como si los bits representaran números enteros de magnitud de signo , aunque no está claro si esto fue una consideración de diseño (parece digno de mención que la representación de punto flotante hexadecimal anterior de IBM también tenía esta propiedad para números normalizados). Con la representación de complemento a dos predominante , interpretar los bits como números enteros con signo ordena los positivos correctamente, pero con los negativos invertidos; como una posible corrección para eso, con un xor para invertir el bit de signo para valores positivos y todos los bits para valores negativos, todos los valores se vuelven ordenables como números enteros sin signo (con −0 < +0 ). ^[35]

Recomendaciones

Manejo alternativo de excepciones

El estándar recomienda el manejo de excepciones opcional en varias formas, incluyendo la presustitución de valores predeterminados definidos por el usuario, y trampas (excepciones que cambian el flujo de control de alguna manera) y otros modelos de manejo de excepciones que interrumpen el flujo, como try/catch. Las trampas y otros mecanismos de excepción siguen siendo opcionales, como lo eran en IEEE 754-1985.

Operaciones recomendadas

La cláusula 9 de la norma recomienda operaciones matemáticas adicionales ^[45] que las normas lingüísticas deberían definir. ^[46] No se requiere ninguna para cumplir con la norma.

Las siguientes son operaciones aritméticas recomendadas, que deben redondearse correctamente: ^[47]

• ${\displaystyle e^{x}}$, , ${\displaystyle 2^{x}}$ ${\displaystyle 10^{x}}$
• ${\displaystyle e^{x}-1}$, , ${\displaystyle 2^{x}-1}$ ${\displaystyle 10^{x}-1}$
• ${\displaystyle \ln x}$, , ${\displaystyle \log _{2}x}$ ${\displaystyle \log _{10}x}$
• ${\displaystyle \ln(1+x)}$, , ${\displaystyle \log _{2}(1+x)}$ ${\displaystyle \log _{10}(1+x)}$
• ${\textstyle {\sqrt {x^{2}+y^{2}}}}$
• ${\displaystyle 1{\big /}{\sqrt {x{\vphantom {t}}}}}$
• ${\displaystyle (1+x)^{n}}$para ( compuesto nombrado y utilizado para calcular un crecimiento exponencial , cuya tasa no puede ser menor que −1) ^[48] ${\displaystyle x\geq -1}$
• ${\displaystyle x^{\frac {1}{n}}}$
• ${\displaystyle x^{n}}$, ${\displaystyle x^{y}}$
• ${\displaystyle \sin x}$, , ${\displaystyle \cos x}$ ${\displaystyle \tan x}$
• ${\displaystyle \arcsin x}$, , , ${\displaystyle \arccos x}$ ${\displaystyle \arctan x}$ ${\displaystyle \operatorname {atan2} (y,x)}$
• ${\displaystyle \operatorname {sinPi} x=\sin \pi x}$, , (ver también: Múltiplos de π ) ${\displaystyle \operatorname {cosPi} x=\cos \pi x}$ ${\displaystyle \operatorname {tanPi} x=\tan \pi x}$
• ${\displaystyle \operatorname {asinPi} x={\tfrac {1}{\pi }}\arcsin x}$, , , (ver también: Múltiplos de π ) ${\displaystyle \operatorname {acosPi} x={\tfrac {1}{\pi }}\arccos x}$ ${\displaystyle \operatorname {atanPi} x={\tfrac {1}{\pi }}\arctan x}$ ${\displaystyle \operatorname {atan2Pi} (y,x)={\tfrac {1}{\pi }}\operatorname {atan2} (y,x)}$
• ${\displaystyle \sinh x}$, , ${\displaystyle \cosh x}$ ${\displaystyle \tanh x}$
• ${\displaystyle \operatorname {arsinh} x}$, , ${\displaystyle \operatorname {arcosh} x}$ ${\displaystyle \operatorname {artanh} x}$

Las funciones , y no formaban parte del estándar IEEE 754-2008 porque se consideraban menos necesarias. ^[49] y se mencionaron, pero esto se consideró un error. ^[5] Las tres se agregaron en la revisión de 2019. ${\displaystyle \operatorname {asinPi} }$ ${\displaystyle \operatorname {acosPi} }$ ${\displaystyle \operatorname {tanPi} }$ ${\displaystyle \operatorname {asinPi} }$ ${\displaystyle \operatorname {acosPi} }$

Las operaciones recomendadas también incluyen la configuración y el acceso a la dirección de redondeo del modo dinámico, ^[50] y operaciones de reducción vectorial definidas por la implementación, como suma, producto escalado y producto escalar , cuya precisión no está especificada por el estándar. ^[51]

A partir de 2019 ^[update], también se recomiendan operaciones aritméticas aumentadas ^[52] para los formatos binarios. Estas operaciones, especificadas para la suma, la resta y la multiplicación, producen un par de valores que consisten en un resultado correctamente redondeado al más cercano en el formato y el término de error, que se puede representar exactamente en el formato. En el momento de la publicación de la norma, no se conocen implementaciones de hardware, pero ya se habían implementado operaciones muy similares en software utilizando algoritmos bien conocidos. La historia y la motivación para su estandarización se explican en un documento de referencia. ^{[53] [54]}

A partir de 2019, los valores minNum , maxNum , minNumMag y maxNumMag que antes se requerían en IEEE 754-2008 ahora están obsoletos debido a su falta de asociatividad . En su lugar, se recomiendan dos conjuntos de nuevas operaciones mínimas y máximas. ^[55] El primer conjunto contiene minimum , minimumNumber , maximum y maximumNumber . El segundo conjunto contiene minimumMagnitude , minimumMagnitudeNumber , maximumMagnitude y maximumMagnitudeNumber . La historia y la motivación de este cambio se explican en un documento de antecedentes. ^[56]

Evaluación de expresión

El estándar recomienda cómo los estándares de lenguaje deberían especificar la semántica de las secuencias de operaciones y señala las sutilezas de los significados literales y las optimizaciones que cambian el valor de un resultado. Por el contrario, la versión anterior de 1985 del estándar dejaba sin especificar aspectos de la interfaz del lenguaje, lo que conducía a un comportamiento inconsistente entre compiladores o a diferentes niveles de optimización en un compilador optimizador .

Los lenguajes de programación deberían permitir que el usuario especifique una precisión mínima para los cálculos intermedios de expresiones para cada base. Esto se conoce como preferenceWidth en el estándar y debería ser posible establecerlo por bloque. Los cálculos intermedios dentro de las expresiones deberían calcularse, y cualquier valor temporal guardado, utilizando el máximo del ancho de los operandos y el ancho preferido si está establecido. Así, por ejemplo, un compilador que apunta a hardware de punto flotante x87 debería tener un medio para especificar que los cálculos intermedios deben utilizar el formato de doble extensión . El valor almacenado de una variable siempre debe utilizarse al evaluar expresiones posteriores, en lugar de cualquier precursor anterior al redondeo y la asignación a la variable.

Reproducibilidad

La versión IEEE 754-1985 del estándar permitía muchas variaciones en las implementaciones (como la codificación de algunos valores y la detección de ciertas excepciones). La IEEE 754-2008 ha reducido estas concesiones, pero aún quedan algunas variaciones (especialmente para formatos binarios). La cláusula de reproducibilidad recomienda que los estándares de lenguaje proporcionen un medio para escribir programas reproducibles (es decir, programas que produzcan el mismo resultado en todas las implementaciones de un lenguaje) y describe lo que se debe hacer para lograr resultados reproducibles.

Representación de personajes

La norma exige operaciones para convertir entre formatos básicos y formatos de secuencias de caracteres externos . ^[57] Se requieren conversiones hacia y desde un formato de caracteres decimales para todos los formatos. La conversión a una secuencia de caracteres externa debe ser tal que la conversión de vuelta usando el redondeo al número más cercano, los empates al número par, recupere el número original. No existe ningún requisito para preservar la carga útil de un NaN silencioso o un NaN de señalización, y la conversión desde la secuencia de caracteres externa puede convertir un NaN de señalización en un NaN silencioso.

El valor binario original se conservará al convertirlo a decimal y viceversa usando: ^[58]

• 5 dígitos decimales para binario16,
• 9 dígitos decimales para binary32,
• 17 dígitos decimales para binary64,
• 36 dígitos decimales para binario128.

Para otros formatos binarios, el número requerido de dígitos decimales es ^[h]

${\displaystyle 1+\lceil p\log _{10}(2)\rceil ,}$

donde p es el número de bits significativos en el formato binario, por ejemplo, 237 bits para binario256.

Al utilizar un formato de punto flotante decimal, la representación decimal se conservará mediante:

• 7 dígitos decimales para decimal32,
• 16 dígitos decimales para decimal64,
• 34 dígitos decimales para decimal128.

^{Gay [59} ] analiza algoritmos, con código, para la conversión redondeada correcta de binario a decimal y de decimal a binario, y Paxson y Kahan ^{[60] , para la prueba.}

Literales hexadecimales

El estándar recomienda proporcionar conversiones hacia y desde secuencias de caracteres externos con significado hexadecimal , basándose en los literales de punto flotante hexadecimales de C99+ . Un literal de este tipo consta de un signo opcional ( o -), el indicador "0x", un número hexadecimal con o sin punto, un indicador de exponente "p" y un exponente decimal con un signo opcional. La sintaxis no distingue entre mayúsculas y minúsculas. ^[61] El exponente decimal se escala en potencias de 2. Por ejemplo, 0x0.1p0es 1/16 y 0x0.1p-4es 1/256. ^[62]

Véase también

• formato de punto flotante bfloat16
• Binadera
• Coprocesador
• C99 para ejemplos de código que demuestran el acceso y uso de las funciones IEEE 754
• Aritmética de punto flotante , para conocer la historia, la justificación del diseño y el uso de ejemplos de las características de IEEE 754
• Aritmética de punto fijo , para un enfoque alternativo en el cálculo con números racionales (especialmente beneficioso cuando el rango del exponente es conocido, fijo o limitado en el momento de la compilación)
• IBM System z9 , la primera CPU que implementó la aritmética decimal IEEE 754-2008 (utilizando microcódigo de hardware)
• IBM z10 , IBM z196 , IBM zEC12 e IBM z13 , CPU que implementan completamente la aritmética decimal IEEE 754-2008 en hardware
• ISO/IEC 10967 , aritmética independiente del lenguaje (LIA)
• Minifloat , formatos binarios de punto flotante de baja precisión que siguen los principios IEEE 754
• CPU POWER6 , POWER7 y POWER8 que implementan completamente la aritmética decimal IEEE 754-2008 en hardware
• strictfp , una palabra clave obsoleta en el lenguaje de programación Java que anteriormente restringía la aritmética a la precisión simple y doble IEEE 754 para garantizar la reproducibilidad en las plataformas de hardware comunes (a partir de Java 17, este comportamiento es obligatorio)
• El dilema del fabricante de tablas: más información sobre el redondeo correcto de funciones
• Entorno numérico estándar de Apple
• Punto flotante cónico
• Posit , un formato de número alternativo

Notas

1. Por ejemplo, si la base es 10, el signo es 1 (que indica negativo), la mantisa es 12345 y el exponente es −3, entonces el valor del número es (−1) ¹ × 12345 × 10 ⁻³ = −1 × 12345 × 0,001 = −12,345.
2. Valores aproximados. Para conocer los valores exactos, consulte la entrada de Wikipedia correspondiente a cada formato.
3. Número de dígitos en la base utilizada, incluido cualquier dígito implícito, pero sin contar el bit de signo.
4. Número correspondiente de dígitos decimales, ver texto para más detalles.
5. A diferencia del sistema decimal, no existe un formato binario de intercambio de 96 bits. Sin embargo, este formato se permite como formato no intercambiable.
6. El estándar recomienda 0 para NaNs de señalización, 1 para NaNs silenciosos, de modo que un NaNs de señalización se puede silenciar cambiando solo este bit a 1, mientras que lo inverso podría producir la codificación de un infinito.
7. No se levanta ninguna bandera en ciertos casos de desbordamiento.
8. Como límite de implementación, el redondeo correcto solo se garantiza para la cantidad de dígitos decimales requerida más 3 para el formato binario admitido más grande. Por ejemplo, si binary32 es el formato binario admitido más grande, entonces se garantiza que una conversión de una secuencia externa decimal con 12 dígitos decimales se redondeará correctamente cuando se convierta a binary32; pero no así la conversión de una secuencia de 13 dígitos decimales; sin embargo, el estándar recomienda que las implementaciones no impongan dicho límite.

Referencias

1. IEEE 754 2019
2. Haasz, Jodi. "FW: ISO/IEC/IEEE 60559 (IEEE Std 754-2008)". IEEE . Archivado desde el original el 2017-10-27 . Consultado el 2018-04-04 .
3. "Acuerdo de cooperación de la Organización de desarrollo de normas asociadas (PSDO) ISO/IEEE" (PDF) . ISO. 2007-12-19 . Consultado el 2021-12-27 .
4. Norma ISO/IEC JTC 1/SC 25 2011.
5. Cowlishaw, Mike (13 de noviembre de 2013). "Fe de erratas de IEEE 754-2008". speleotrove.com . Consultado el 24 de enero de 2020 .
6. "ANSI/IEEE Std 754-2019". ucbtest.org . Consultado el 16 de enero de 2024 .
7. Norma ISO/IEC JTC 1/SC 25 2020.
8. "Cuestiones para la próxima revisión de 754". IEEE . Consultado el 12 de agosto de 2024 .
9. IEEE 754 2008, §2.1.27.
10. "SpiderMonkey Internals" (Interiores de SpiderMonkey). udn.realityripple.com . Consultado el 11 de marzo de 2018 .
11. Klemens, Ben (septiembre de 2014). 21st Century C: C Tips from the New School. O'Reilly Media, Incorporated. pág. 160. ISBN 9781491904442. Recuperado el 11 de marzo de 2018 .
12. "zuiderkwast/nanbox: NaN-boxing en C". GitHub . Consultado el 11 de marzo de 2018 .
13. IEEE 754 2008, §3.6.
14. IEEE 754 2008, §3.7.
15. IEEE 754 2008, §3.7 establece: "Los estándares del lenguaje deben definir mecanismos que respalden la precisión extensible para cada base admitida".
16. IEEE 754 2008, §3.7 establece: "Los estándares o implementaciones del lenguaje deben admitir un formato de precisión extendida que amplíe el formato básico más amplio admitido en esa base".
17. Familia Motorola MC68000 (PDF) . Manual de referencia del programador. NXP Semiconductors. 1992. págs. 1–16, 1–18, 1–23.
18. IEEE 754 2008, §4.3.1. "En los dos atributos de dirección de redondeo siguientes, un resultado infinitamente preciso con una magnitud de al menos se redondeará a sin cambio de signo". ${\displaystyle b^{\text{emax}}(b-{\tfrac {1}{2}}b^{1-p})}$ ${\displaystyle \infty }$
19. IEEE 754 2008, §4.3.3
20. IEEE 754 2019, §2.1
21. IEEE 754 2008, §5.3.1
22. IEEE 754 2008, §5.4.1
23. IEEE 754 2008, §5.4.2
24. IEEE 754 2008, §5.4.3
25. IEEE 754 2008, §5.3.2
26. IEEE 754 2008, §5.3.3
27. IEEE 754 2008, §5.5.1
28. IEEE 754 2008, §5.10
29. IEEE 754 2008, §5.11
30. IEEE 754 2008, §5.7.2
31. IEEE 754 2008, §5.7.4
32. IEEE 754 2019, §5.11
33. IEEE 754 2019, §5.10
34. "Implementar total_cmp para f32, f64 por golddranks · Solicitud de incorporación de cambios n.° 72568 · rust-lang/rust". GitHub .– contiene citas relevantes de IEEE 754-2008 y -2019. Contiene una implementación y explicación de un juego de palabras.
35. Herf, Michael (diciembre de 2001). "trucos de radix". estereopsis: gráficos .
36. "9.4. decimal — Aritmética decimal de punto fijo y punto flotante — Documentación de Python 3.6.5". docs.python.org . Consultado el 4 de abril de 2018 .
37. "Aritmética decimal - Condiciones excepcionales". speleotrove.com . Consultado el 4 de abril de 2018 .
38. IEEE 754 2008, §7.2(h)
39. Goldberg 1991.
40. Müller, Jean-Michel; Brisebarre, Nicolás; de Dinechin, Florent; Jeannerod, Claude-Pierre; Lefèvre, Vicente; Melquiond, Guillaume; Revol, Nathalie ; Stehlé, Damián; Torres, Serge (2010). Manual de aritmética de coma flotante (1 ed.). Birkhäuser . doi :10.1007/978-0-8176-4705-6. ISBN 978-0-8176-4704-9. Número de serie LCCN  2009939668.
41. Kahan, William Morton ; Darcy, Joseph (2001) [1998-03-01]. "Cómo el punto flotante de Java perjudica a todos en todas partes" (PDF) . Archivado (PDF) desde el original el 2000-08-16 . Consultado el 2003-09-05 .
42. Kahan, William Morton (12 de febrero de 1981). "¿Por qué necesitamos un estándar aritmético de punto flotante?" (PDF) . pág. 26. Archivado (PDF) desde el original el 4 de diciembre de 2004.
43. Severance, Charles (20 de febrero de 1998). "Una entrevista con el anciano del punto flotante".
44. Kahan, William Morton (11 de junio de 1996). "El efecto nefasto de los puntos de referencia informáticos en las matemáticas aplicadas, la física y la química" (PDF) . Archivado (PDF) desde el original el 13 de octubre de 2013.
45. IEEE 754 2019, §9.2
46. IEEE 754 2008, Cláusula 9
47. IEEE 754 2019, §9.2.
48. "Demasiada potencia: pow vs powr, powd, pown, rootn, compuesto". IEEE . Consultado el 16 de enero de 2024 . Dado que las tasas de crecimiento no pueden ser inferiores a -1, dichas tasas indican excepciones no válidas.
49. "Re: Funciones faltantes tanPi, asinPi y acosPi". IEEE . Archivado desde el original el 2017-07-06 . Consultado el 2018-04-04 .
50. IEEE 754 2008, §9.3.
51. IEEE 754 2008, §9.4.
52. IEEE 754 2019, §9.5
53. Riedy, Jason; Demmel, James. "Operaciones aritméticas aumentadas propuestas para IEEE-754 2018" (PDF) . 25.º Simbosio IEEE sobre aritmética informática (ARITH 2018). págs. 49–56. Archivado (PDF) desde el original el 23 de julio de 2019. Consultado el 23 de julio de 2019 .
54. "ANSI/IEEE Std 754-2019 – Documentos de referencia". IEEE . Consultado el 16 de enero de 2024 .
55. IEEE 754 2019, §9.6.
56. Chen, David. "La eliminación/degradación de las operaciones MinNum y MaxNum de IEEE 754-2018" (PDF) . IEEE . Consultado el 16 de enero de 2024 .
57. IEEE 754 2008, §5.12.
58. IEEE 754 2008, §5.12.2.
59. Gay, David M. (30 de noviembre de 1990), Conversiones binario-decimal y decimal-binario correctamente redondeadas, Manuscrito de análisis numérico, Murry Hill, NJ, EE. UU.: AT&T Laboratories, 90-10
60. Paxson, Vern; Kahan, William (22 de mayo de 1991), Un programa para probar la conversión de decimales a binarios IEEE , Manuscrito, CiteSeerX 10.1.1.144.5889 
61. IEEE 754 2008, §5.12.3
62. "6.9.3. Literales de punto flotante hexadecimales — Guía del usuario de Glasgow Haskell Compiler 9.3.20220129". ghc.gitlab.haskell.org . Consultado el 29 de enero de 2022 .

Normas

• Estándar IEEE para aritmética binaria de punto flotante . ANSI/IEEE STD 754-1985. IEEE. 12 de octubre de 1985. págs. 1–20. doi :10.1109/IEEESTD.1985.82928. ISBN . 0-7381-1165-1.
• IEEE Computer Society (29 de agosto de 2008). Estándar IEEE para aritmética de punto flotante . IEEE STD 754-2008. IEEE. págs. 1–70. doi :10.1109/IEEESTD.2008.4610935. ISBN . 978-0-7381-5753-5. Norma IEEE 754-2008.
• IEEE Computer Society (22 de julio de 2019). Estándar IEEE para aritmética de punto flotante . IEEE STD 754-2019. IEEE. págs. 1–84. doi :10.1109/IEEESTD.2019.8766229. ISBN . 978-1-5044-5924-2. Norma IEEE 754-2019.
• ISO/IEC JTC 1/SC 25 (junio de 2011). ISO/IEC/IEEE 60559:2011 — Tecnología de la información — Sistemas de microprocesadores — Aritmética de punto flotante. ISO. págs. 1–58.{{cite book}}: CS1 maint: numeric names: authors list (link)
• ISO/IEC JTC 1/SC 25 (mayo de 2020). ISO/IEC 60559:2020 — Tecnología de la información — Sistemas de microprocesadores — Aritmética de punto flotante . ISO. págs. 1–74.{{cite book}}: CS1 maint: numeric names: authors list (link)

Referencias secundarias

• Aritmética decimal de punto flotante, preguntas frecuentes, bibliografía y enlaces
• Comparación de flotantes binarios
• Material de referencia IEEE 754
• IEEE 854-1987 – Historia y actas
• Lecturas complementarias para IEEE 754. Incluye perspectivas históricas.

Lectura adicional

• Goldberg, David (marzo de 1991). "Lo que todo informático debería saber sobre aritmética de punto flotante". ACM Computing Surveys . 23 (1): 5–48. doi : 10.1145/103162.103163 . S2CID  222008826.(Con el apéndice "Diferencias entre las implementaciones de IEEE 754": [1], [2])
• Hecker, Chris (febrero de 1996). "Lleguemos al punto (flotante)" (PDF) . Revista Game Developer : 19–24. ISSN  1073-922X.
• Severance, Charles (marzo de 1998). "IEEE 754: una entrevista con William Kahan" (PDF) . IEEE Computer . 31 (3): 114–115. doi :10.1109/MC.1998.660194. S2CID  33291145 . Consultado el 8 de marzo de 2019 .
• Cowlishaw, Mike (junio de 2003). "Coma flotante decimal: algoritmo para computadoras". 16.° Simposio IEEE sobre aritmética informática, 2003. Actas (PDF) . Los Alamitos, California: IEEE Computer Society. págs. 104–111. doi :10.1109/ARITH.2003.1207666. ISBN . 978-0-7695-1894-7. S2CID  18713046 . Consultado el 14 de noviembre de 2014 .. (Nota: Algorismo no es un error ortográfico del título; véase también algoritmo ).
• Monniaux, David (mayo de 2008). "Los escollos de verificar cálculos de punto flotante". ACM Transactions on Programming Languages ​​and Systems . 30 (3): 1–41. arXiv : cs/0701192 . doi :10.1145/1353445.1353446. ISSN  0164-0925. S2CID  218578808.:Un compendio de comportamientos no intuitivos del punto flotante en arquitecturas populares, con implicaciones para la verificación y prueba de programas.
• Müller, Jean-Michel; Brunie, Nicolás; de Dinechin, Florent; Jeannerod, Claude-Pierre; Joldes, Mioara; Lefèvre, Vicente; Melquiond, Guillaume; Revol, Nathalie ; Torres, Serge (2018) [2010]. Manual de aritmética de coma flotante (2 ed.). Birkhäuser . doi :10.1007/978-3-319-76526-6. ISBN 978-3-319-76525-9.
• Overton, Michael L. (2001). Escrito en el Courant Institute of Mathematical Sciences , New York University , Nueva York, EE. UU. , Computación numérica con aritmética de punto flotante IEEE (1.ª ed.). Filadelfia, EE. UU.: SIAM . doi :10.1137/1.9780898718072. ISBN. 978-0-89871-482-1. 978-0-89871-571-2, 0-89871-571-7.
• Cleve Moler sobre los números de punto flotante
• Beebe, Nelson HF (22 de agosto de 2017). Manual de cálculo de funciones matemáticas: programación con la biblioteca de software portátil MathCW (1.ª edición). Salt Lake City, UT, EE. UU.: Springer International Publishing AG . doi :10.1007/978-3-319-64110-2. ISBN. 978-3-319-64109-6. Código LCCN  2017947446. S2CID  30244721.
• Hough, David G. (diciembre de 2019). "El estándar IEEE 754: uno para los libros de historia". Computer . 52 (12). IEEE : 109–112. doi :10.1109/MC.2019.2926614. S2CID  208281213.

Enlaces externos

• Kahan sobre la creación del estándar IEEE de punto flotante. Clips de los ganadores del premio Turing . 2020-11-16. Archivado desde el original el 2021-11-08.