Puente anular

Afirmación de que los ángulos opuestos a los lados iguales de un triángulo isósceles son ellos mismos iguales

El pons asinorum en la edición de los Elementos de Oliver Byrne ^[1]

En geometría , el teorema de que los ángulos opuestos a los lados iguales de un triángulo isósceles son en sí mismos iguales se conoce como pons asinorum (/ˈpɒnzˌæsɪˈnɔːrəm / PONZ ass - ih - NOR - əm ) , en latín "puente de asnos ", o más descriptivamente como el teorema del triángulo isósceles . El teorema aparece como Proposición 5 del Libro 1 de los Elementos de Euclides . [ 1 ^] Su recíproco también es cierto: si dos ángulos de un triángulo son iguales, entonces los lados opuestos a ellos también son iguales.

Pons asinorum también se utiliza metafóricamente para designar un problema o desafío que actúa como prueba del pensamiento crítico , en referencia a la capacidad del "puente de los asnos" para separar a los razonadores capaces de los incapaces. Su primer uso conocido en este contexto fue en 1645. ^[2]

Etimología

Existen dos explicaciones comunes para el nombre pons asinorum , la más simple es que el diagrama utilizado se asemeja a un puente físico . Pero la explicación más popular es que es la primera prueba real en los Elementos de la inteligencia del lector y funciona como un "puente" hacia las proposiciones más difíciles que siguen. ^[3]

Otro término medieval para el teorema del triángulo isósceles era Elefuga , que, según Roger Bacon , proviene del griego elegia, «miseria», y del latín fuga , «huida», es decir, «huida de los desgraciados». Aunque esta etimología es dudosa, se refleja en el uso que hace Chaucer del término «flemyng of wreches» para referirse al teorema. ^[4]

El nombre Dulcarnon se le dio a la 47.ª proposición del Libro I de Euclides, más conocida como el teorema de Pitágoras , en honor al árabe Dhū 'l qarnain ذُو ٱلْقَرْنَيْن, que significa "el dueño de los dos cuernos", porque los diagramas del teorema mostraban dos cuadrados más pequeños como cuernos en la parte superior de la figura. Ese término también se ha utilizado como metáfora de un dilema. ^[4] El nombre pons asinorum se ha aplicado ocasionalmente al teorema de Pitágoras. ^[5]

Carl Friedrich Gauss supuestamente sugirió una vez que comprender la identidad de Euler podría desempeñar un papel similar, como punto de referencia que indicara si alguien podía convertirse en un matemático de primera clase . ^[6]

Pruebas

Euclides y Proclo

La afirmación de Euclides sobre el pons asinorum incluye una segunda conclusión: si los lados iguales del triángulo se prolongan por debajo de la base, entonces los ángulos entre las prolongaciones y la base también son iguales. La prueba de Euclides implica trazar líneas auxiliares hasta estas prolongaciones. Pero, como señala Proclo , comentarista de Euclides , Euclides nunca utiliza la segunda conclusión y su prueba se puede simplificar un poco trazando las líneas auxiliares hasta los lados del triángulo, y el resto de la prueba se desarrolla más o menos de la misma manera.

Se ha especulado y debatido mucho sobre por qué Euclides añadió la segunda conclusión al teorema, dado que hace que la prueba sea más complicada. Una explicación plausible, dada por Proclo, es que la segunda conclusión puede usarse en posibles objeciones a las pruebas de proposiciones posteriores donde Euclides no cubre todos los casos. ^[7] La ​​prueba se basa en gran medida en lo que hoy se llama lado-ángulo-lado (SAS), la proposición anterior en los Elementos , que dice que dados dos triángulos para los cuales dos pares de lados correspondientes y sus ángulos incluidos son respectivamente congruentes , entonces los triángulos son congruentes.

La variación de Proclo de la prueba de Euclides procede de la siguiente manera: ^[8] Sea ⁠ ⁠ ${\displaystyle \triangle ABC}$ un triángulo isósceles con lados congruentes ⁠ ⁠ ${\displaystyle AB\cong AC}$ . Elija un punto arbitrario ⁠ ⁠ ${\displaystyle D}$ a lo largo del lado ⁠ ⁠ ${\displaystyle AB}$ y luego construya el punto ⁠ ⁠ ${\displaystyle E}$ en ⁠ ⁠ ${\displaystyle AC}$ para hacer segmentos congruentes ⁠ ⁠ ${\displaystyle AD\cong AE}$ . Dibuje segmentos de línea auxiliares ⁠ ⁠ ${\displaystyle BE}$ , ⁠ ⁠ ${\displaystyle DC}$ , y ⁠ ⁠ ${\displaystyle DE}$ . Por lado-ángulo-lado, los triángulos ⁠ ⁠ ${\displaystyle \triangle BAE\cong \triangle CAD}$ . Por lo tanto ⁠ ⁠ ${\displaystyle \angle ABE\cong \angle ACD}$ , ⁠ ⁠ ${\displaystyle \angle ADC\cong \angle AEB}$ , y ⁠ ⁠ ${\displaystyle BE\cong CD}$ . Restando segmentos de línea congruentes, ⁠ ⁠ ${\displaystyle BD\cong CE}$ . Esto establece otro par de triángulos congruentes, ⁠ ⁠ ${\displaystyle \triangle DBE\cong \triangle ECD}$ , nuevamente por lado-ángulo-lado. Por lo tanto ⁠ ⁠ ${\displaystyle \angle BDE\cong \angle CED}$ y ⁠ ⁠ ${\displaystyle \angle BED\cong \angle CDE}$ . Restando ángulos congruentes, ⁠ ⁠ ${\displaystyle \angle BDC\cong \angle CEB}$ . Finalmente ⁠ ⁠ ${\displaystyle \triangle BDC\cong \triangle CEB}$ por una tercera aplicación de lado-ángulo-lado. Por lo tanto ⁠ ⁠ ${\displaystyle \angle CBD\cong \angle BCE}$ , lo cual se debía demostrar.

Pappus

Proclo ofrece una prueba mucho más breve, atribuida a Pappus de Alejandría . No sólo es más sencilla, sino que no requiere ninguna construcción adicional. El método de prueba consiste en aplicar lado-ángulo-lado al triángulo y su imagen especular. Autores más modernos, imitando el método de prueba dado para la proposición anterior, han descrito esto como levantar el triángulo, darle la vuelta y colocarlo sobre sí mismo. ^{[9] [10]} Este método es satirizado por Charles Dodgson en Euclides y sus rivales modernos , llamándolo un " toro irlandés " porque aparentemente requiere que el triángulo esté en dos lugares a la vez. ^[11]

La prueba es la siguiente: ^[12] Sea ABC un triángulo isósceles con AB y AC como lados iguales. Considérense los triángulos ABC y ACB , donde ACB se considera un segundo triángulo con vértices A , C y B correspondientes respectivamente a A , B y C en el triángulo original. es igual a sí mismo, AB  =  AC y AC  =  AB , por lo que por lado-ángulo-lado, los triángulos ABC y ACB son congruentes. En particular, . ^[13] ${\displaystyle \angle A}$ ${\displaystyle \angle B=\angle C}$

Otros

Una prueba de libro de texto

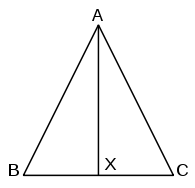
Un método estándar en los libros de texto es construir la bisectriz del ángulo en A. ^[14] Esto es más simple que la prueba de Euclides, pero Euclides no presenta la construcción de una bisectriz de un ángulo hasta la proposición 9. Por lo tanto , el orden de presentación de las proposiciones de Euclides tendría que cambiarse para evitar la posibilidad de un razonamiento circular.

La prueba se realiza de la siguiente manera: ^[15] Como antes, sea el triángulo ABC con AB  =  AC . Construya la bisectriz del ángulo de y prolongérela para cortar BC en X . AB  =  AC y AX es igual a sí mismo. Además, , por lo que, aplicando lado-ángulo-lado, el triángulo BAX y el triángulo CAX son congruentes. Se deduce que los ángulos en B y C son iguales. ${\displaystyle \angle BAC}$ ${\displaystyle \angle BAX=\angle CAX}$

Legendre utiliza una construcción similar en Elementos de geometría , pero tomando X como el punto medio de BC . ^[16] La prueba es similar, pero se debe utilizar lado-lado-lado en lugar de lado-ángulo-lado, y lado-lado-lado no es dado por Euclides hasta más adelante en Elementos .

En 1876, mientras era miembro del Congreso de los Estados Unidos , el futuro presidente James A. Garfield desarrolló una prueba usando el trapezoide, que fue publicada en el New England Journal of Education . ^[17] El historiador de matemáticas William Dunham escribió que el trabajo de Garfield sobre el trapezoide era "realmente una prueba muy inteligente". ^[18] Según el Journal , Garfield llegó a la prueba "en diversiones matemáticas y discusiones con otros miembros del congreso". ^[19]

En espacios interiores de productos

El teorema del triángulo isósceles se cumple en espacios de producto interno sobre los números reales o complejos . En tales espacios, dados los vectores x , y y z , el teorema dice que si y entonces ${\displaystyle x+y+z=0}$ ${\displaystyle \|x\|=\|y\|,}$ ${\displaystyle \|x-z\|=\|y-z\|.}$

Dado que y donde θ es el ángulo entre los dos vectores, la conclusión de esta forma de espacio de producto interno del teorema es equivalente a la afirmación sobre la igualdad de ángulos. ${\displaystyle \|x-z\|^{2}=\|x\|^{2}-2x\cdot z+\|z\|^{2}}$ ${\displaystyle x\cdot z=\|x\|\|z\|\cos \theta ,}$

Uso metafórico

Los usos del pons asinorum como metáfora para una prueba de pensamiento crítico incluyen:

• El Filobiblon del siglo XIV de Richard Aungerville contiene el pasaje "¡Quot Euclidis discipulos retrojecit Elefuga quasi scopulos eminens et abruptus, qui nullo scalarum suffragio scandi posset! Durus, inquiunt, est his sermo; quis potest eum audire?", que compara el teorema con un acantilado escarpado que ninguna escalera puede ayudar a escalar y pregunta cuántos aspirantes a geómetras han sido rechazados. ^[4]
• El término pons asinorum , tanto en su significado de puente como de prueba, se utiliza como metáfora para encontrar el término medio de un silogismo . ^[4]
• El poeta del siglo XVIII Thomas Campbell escribió un poema humorístico llamado "Pons asinorum" donde una clase de geometría ataca el teorema como una compañía de soldados podría atacar una fortaleza; la batalla no estuvo exenta de bajas. ^[20]
• El economista John Stuart Mill llamó a la Ley de la Renta de Ricardo el "pons asinorum de la economía". ^[21]
• El finlandés aasinsilta y el sueco åsnebrygga son técnicas literarias en las que se utiliza una conexión tenue, incluso artificial, entre dos argumentos o temas, que es casi pero no exactamente un non sequitur , como una transición incómoda entre ellos. En un texto serio, se considera un error de estilo, ya que pertenece propiamente al estilo de escritura de flujo de conciencia o causerie . Ejemplos típicos son terminar una sección diciendo de qué trata la siguiente sección, sin molestarse en explicar por qué los temas están relacionados, ampliar una mención casual en un tratamiento detallado o encontrar una conexión artificial entre los temas (por ejemplo, "Compramos un poco de vino tinto; hablando de líquidos rojos, mañana es el Día Mundial del Donante de Sangre").
• En holandés , ezelsbruggetje ('puente de burros') es la palabra que designa una regla mnemotécnica . Lo mismo se aplica al alemán Eselsbrücke .
• En checo , oslí můstek tiene dos significados: puede describir una conexión artificial entre dos temas o una regla mnemotécnica.

Mito de la prueba de la inteligencia artificial

Una persistente pieza del folclore matemático afirma que un programa de inteligencia artificial descubrió una prueba original y más elegante de este teorema. ^{[22] [23]} De hecho, Marvin Minsky cuenta que había redescubierto la prueba de Pappus (de la que no era consciente) simulando lo que un demostrador mecánico de teoremas podría hacer. ^{[24] [10]}

Notas

1. Byrne, Oliver (1847). Los seis primeros libros de Los elementos de Euclides en los que se utilizan diagramas y símbolos de colores en lugar de letras para facilitar el aprendizaje . Taschen. pp. Página 5. ISBN 978-1528770439.
2. "Pons asinorum". Diccionario Merriam-Webster.com .
3. DE Smith Historia de las matemáticas (1958 Dover) pág. 284
4. AF West y HD Thompson "Sobre Dulcarnon, Elefuga y Pons Asinorum como nombres fantásticos para proposiciones geométricas" The Princeton University bulletin Vol. 3 No. 4 (1891) p. 84
5. Smith, David Eugene (1925). Historia de las matemáticas. Vol. 2. Ginn & Co., pág. 284, nota al pie 1.
6. Derbyshire, John (2003). La obsesión primordial: Bernhard Riemann y el mayor problema no resuelto de las matemáticas . 500 Fifth Street, NW, Washington DC 20001: Joseph Henry Press. pág. 202. ISBN 0-309-08549-7.matemático de primera clase.{{cite book}}: CS1 maint: location (link)
7. Heath págs. 251–255
8. Siguiendo a Proclo p. 53
9. Por ejemplo, F. Cuthbertson Primer of geometry (1876 Oxford) pág. 7
10. Michael AB Deakin, "De Pappus a la actualidad: la historia de una prueba", The Mathematical Gazette 74 :467:6-11 (marzo de 1990) JSTOR  3618841
11. Charles Lutwidge Dodgson, Euclides y sus rivales modernos Acto I Escena II §6
12. Siguiendo a Proclo p. 54
13. Heath p. 254 para la sección
14. Por ejemplo, JM Wilson , Geometría elemental (1878, Oxford), pág. 20
15. Siguiendo a Wilson
16. AM Legendre Éléments de géométrie (1876 Libr. de Firmin-Didot et Cie) p. 14
17. G., JA (1876). "Pons Asinorum". Revista de Educación de Nueva Inglaterra . 3 (14): 161. ISSN  2578-4145. JSTOR  44764657.
18. Dunham, William (1994). El universo matemático: un viaje alfabético a través de las grandes pruebas, problemas y personalidades . Wiley & Sons. pág. 99. Bibcode :1994muaa.book.....D. ISBN 9780471536567.
19. Kolpas, Sid J. "Tesoro matemático: la prueba de Garfield del teorema de Pitágoras". Asociación Matemática de América. Archivado desde el original el 6 de diciembre de 2021. Consultado el 22 de diciembre de 2021 .
20. Campbell, Thomas (1864). Las obras poéticas de Thomas Campbell. Little, Brown.
21. John Stuart Mill Principios de economía política (1866: Longmans, Green, Reader y Dyer) Libro 2, Capítulo 16, pág. 261
22. Jaakko Hintikka, "Sobre la creatividad en el razonamiento", en Ake E. Andersson, NE Sahlin, eds., La complejidad de la creatividad , 2013, ISBN 9401587884 , pág. 72 
23. A. Battersby, Matemáticas en la gestión , 1966, citado en Deakin
24. Jeremy Bernstein, "Perfiles: IA" (entrevista con Marvin Minsky), The New Yorker 14 de diciembre de 1981, págs. 50-126

Referencias

• Euclides, comentario y traducción de TL Heath Elements Vol. 1 (1908 Cambridge) Google Books
• Euclides, comentario de Proclo , ed. y trad. de T. Taylor Elements Vol. 2 (1789) Google Books

Enlaces externos

• Puente asinorum en PlanetMath .
• Presentación de los Elementos de Euclides por parte de DE Joyce