Estrés del cilindro

Distribución de tensión simétrica rotacional

En mecánica , una tensión cilíndrica es una distribución de tensión con simetría rotacional, es decir, que permanece inalterada si el objeto estresado gira alrededor de algún eje fijo.

Los patrones de tensión del cilindro incluyen:

• tensión circunferencial , o tensión circular , una tensión normal en la dirección tangencial ( azimut ).
• tensión axial , una tensión normal paralela al eje de simetría cilíndrica.
• tensión radial , una tensión normal en direcciones coplanares pero perpendiculares al eje de simetría.

Estas tres tensiones principales (circular, longitudinal y radial) se pueden calcular analíticamente utilizando un sistema de tensiones triaxiales mutuamente perpendiculares. ^[1]

El ejemplo clásico (y homónimo) de tensión circunferencial es la tensión aplicada a las bandas de hierro, o aros, de un barril de madera . En una tubería recta y cerrada , cualquier fuerza aplicada a la pared de la tubería cilíndrica por un diferencial de presión dará lugar en última instancia a tensiones circunferenciales. De manera similar, si esta tubería tiene tapas de extremo planas, cualquier fuerza aplicada a ellas por presión estática inducirá una tensión axial perpendicular en la misma pared de la tubería. Las secciones delgadas a menudo tienen una tensión radial despreciable , pero los modelos precisos de carcasas cilíndricas de paredes más gruesas requieren que se consideren dichas tensiones.

En los recipientes a presión de paredes gruesas, se pueden utilizar técnicas de construcción que permitan patrones de tensión iniciales favorables. Estas tensiones de compresión en la superficie interna reducen la tensión circunferencial general en los cilindros presurizados. Los recipientes cilíndricos de esta naturaleza se construyen generalmente a partir de cilindros concéntricos encogidos (o expandidos) uno sobre otro, es decir, cilindros de ajuste por contracción, pero también se pueden realizar cilindros singulares mediante autofrettage de cilindros gruesos. ^[2]

Definiciones

Estrés del aro

Componentes de la tensión circunferencial

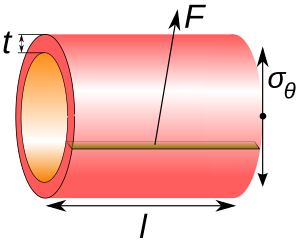
La tensión circunferencial es la fuerza ejercida sobre el área circunferencialmente (perpendicular al eje y al radio del objeto) en ambas direcciones sobre cada partícula en la pared del cilindro. Puede describirse como:

${\displaystyle \sigma _{\theta }={\dfrac {F}{tl}}\ }$

dónde:

• F es la fuerza ejercida circunferencialmente sobre un área de la pared del cilindro que tiene las siguientes dos longitudes como lados:
• t es el espesor radial del cilindro
• l es la longitud axial del cilindro.

Una alternativa a la tensión circunferencial para describir la tensión circunferencial es la tensión de pared ( T ) , que generalmente se define como la fuerza circunferencial total ejercida a lo largo de todo el espesor radial: ^[3]

${\displaystyle T={\dfrac {F}{l}}\ }$

Coordenadas cilíndricas

Junto con la tensión axial y la tensión radial , la tensión circunferencial es un componente del tensor de tensión en coordenadas cilíndricas .

Generalmente resulta útil descomponer cualquier fuerza aplicada a un objeto con simetría rotacional en componentes paralelos a las coordenadas cilíndricas r , z y θ . Estos componentes de fuerza inducen tensiones correspondientes: tensión radial, tensión axial y tensión circunferencial, respectivamente.

Relación con la presión interna

Suposición de paredes delgadas

Para que la suposición de pared delgada sea válida, el recipiente debe tener un espesor de pared de no más de aproximadamente una décima parte (a menudo citado como Diámetro / t > 20) de su radio. ^[4] Esto permite tratar la pared como una superficie y, posteriormente, utilizar la ecuación de Young-Laplace para estimar la tensión circunferencial creada por una presión interna en un recipiente de presión cilíndrico de pared delgada:

${\displaystyle \sigma _{\theta }={\dfrac {Pr}{t}}\ }$ (para un cilindro)

${\displaystyle \sigma _{\theta }={\dfrac {Pr}{2t}}\ }$ (para una esfera)

dónde

• P es la presión interna
• t es el espesor de la pared
• r es el radio medio del cilindro
• ${\displaystyle \sigma _{\theta }\!}$es la tensión del aro.

La ecuación de la tensión circunferencial para conchas delgadas también es aproximadamente válida para recipientes esféricos, incluidas células vegetales y bacterias en las que la presión de turgencia interna puede alcanzar varias atmósferas. En aplicaciones prácticas de ingeniería para cilindros (tuberías y tubos), la tensión circunferencial suele reordenarse para la presión y se denomina fórmula de Barlow .

Las unidades del sistema pulgada-libra-segundo (IPS) para P son libras-fuerza por pulgada cuadrada (psi). Las unidades para t y d son pulgadas (in). Las unidades del SI para P son pascales (Pa), mientras que t y d = 2 r son metros (m).

Cuando el recipiente tiene los extremos cerrados, la presión interna actúa sobre ellos para desarrollar una fuerza a lo largo del eje del cilindro. Esto se conoce como tensión axial y suele ser menor que la tensión circunferencial.

${\displaystyle \sigma _{z}={\dfrac {F}{A}}={\dfrac {Pd^{2}}{(d+2t)^{2}-d^{2}}}\ }$

Aunque esto puede aproximarse a

${\displaystyle \sigma _{z}={\dfrac {Pr}{2t}}\ }$

También existe una tensión radial que se desarrolla perpendicularmente a la superficie y que puede estimarse en cilindros de paredes delgadas como: ${\displaystyle \sigma _{r}\ }$

${\displaystyle \sigma _{r}={-P}\ }$

En el supuesto de paredes delgadas, la relación es grande, por lo que en la mayoría de los casos este componente se considera insignificante en comparación con las tensiones circunferenciales y axiales. ^[5] ${\displaystyle {\dfrac {r}{t}}\ }$

Vasos de paredes gruesas

Cuando el cilindro a estudiar tiene una relación menor que 10 (a menudo citada como ), las ecuaciones del cilindro de paredes delgadas ya no se cumplen ya que las tensiones varían significativamente entre las superficies internas y externas y la tensión cortante a través de la sección transversal ya no se puede descuidar. ${\displaystyle {\text{radius}}/{\text{thickness}}}$ ${\displaystyle {\text{diameter}}/{\text{thickness}}<20}$

Estas tensiones y deformaciones se pueden calcular utilizando las ecuaciones de Lamé , ^[6] un conjunto de ecuaciones desarrolladas por el matemático francés Gabriel Lamé .

${\displaystyle \sigma _{r}=A-{\dfrac {B}{r^{2}}}\ }$

${\displaystyle \sigma _{\theta }=A+{\dfrac {B}{r^{2}}}\ }$

dónde:

${\displaystyle A}$y son constantes de integración, que pueden encontrarse a partir de las condiciones de contorno, ${\displaystyle B}$

${\displaystyle r}$es el radio en el punto de interés (por ejemplo, en las paredes interiores o exteriores).

Para cilindro con condiciones de contorno:

${\displaystyle p(r=a)=P_{a}}$(es decir, presión interna en la superficie interior), ${\displaystyle P_{a}}$

${\displaystyle p(r=b)=P_{b}}$(es decir, presión externa en la superficie exterior), ${\displaystyle P_{b}}$

Se obtienen las siguientes constantes:

${\displaystyle A={\dfrac {P_{a}a^{2}-P_{b}b^{2}}{b^{2}-a^{2}}}\ }$,

${\displaystyle B={\dfrac {a^{2}b^{2}(P_{a}-P_{b})}{b^{2}-a^{2}}}\ }$.

Utilizando estas constantes, se obtiene la siguiente ecuación para la tensión circunferencial:

${\displaystyle \sigma _{\theta }={\dfrac {P_{a}a^{2}-P_{b}b^{2}}{b^{2}-a^{2}}}+{\dfrac {a^{2}b^{2}(P_{a}-P_{b})}{(b^{2}-a^{2})r^{2}}}\ }$

Para un cilindro sólido: entonces y un cilindro sólido no puede tener una presión interna entonces . ${\displaystyle R_{i}=0}$ ${\displaystyle B=0}$ ${\displaystyle A=P_{o}}$

Como para cilindros de paredes gruesas la relación es menor que 10, la tensión radial, en proporción a las otras tensiones, se vuelve no despreciable (es decir, P ya no es mucho, mucho menor que Pr/t y Pr/2t), y por lo tanto el espesor de la pared se convierte en una consideración importante para el diseño (Harvey, 1974, pág. 57). ${\displaystyle {\dfrac {r}{t}}\ }$

En la teoría de los recipientes a presión, cualquier elemento dado de la pared se evalúa en un sistema de tensiones triaxiales, siendo las tres tensiones principales la circunferencial, la longitudinal y la radial. Por lo tanto, por definición, no existen tensiones de corte en los planos transversal, tangencial o radial. ^[1]

En cilindros de paredes gruesas, la tensión de corte máxima en cualquier punto está dada por la mitad de la diferencia algebraica entre las tensiones máxima y mínima, que es, por lo tanto, igual a la mitad de la diferencia entre las tensiones circunferenciales y radiales. La tensión de corte alcanza un máximo en la superficie interna, lo cual es significativo porque sirve como criterio de falla, ya que se correlaciona bien con las pruebas de ruptura reales de cilindros gruesos (Harvey, 1974, p. 57).

Efectos prácticos

Ingeniería

La fractura está determinada por la tensión circunferencial en ausencia de otras cargas externas, ya que es la tensión principal más grande. Nótese que un aro experimenta la mayor tensión en su interior (el exterior y el interior experimentan la misma tensión total, que se distribuye en diferentes circunferencias); por lo tanto, las grietas en las tuberías deberían comenzar teóricamente desde el interior de la tubería. Es por eso que las inspecciones de tuberías después de los terremotos generalmente implican enviar una cámara dentro de una tubería para inspeccionar si hay grietas. La fluencia está determinada por una tensión equivalente que incluye la tensión circunferencial y la tensión longitudinal o radial cuando no existe.

Medicamento

En la patología de las paredes vasculares o gastrointestinales , la tensión de la pared representa la tensión muscular sobre la pared del vaso. Como resultado de la Ley de Laplace , si se forma un aneurisma en la pared de un vaso sanguíneo, el radio del vaso ha aumentado. Esto significa que la fuerza hacia adentro sobre el vaso disminuye y, por lo tanto, el aneurisma continuará expandiéndose hasta romperse. Una lógica similar se aplica a la formación de divertículos en el intestino . ^[7]

Desarrollo de la teoría

Pilar de hierro fundido del puente ferroviario de Chepstow , 1852. Los aros de hierro forjado unidos con pasadores (más resistentes a la tensión que el hierro fundido) resisten las tensiones del aro. ^[8]

El primer análisis teórico de la tensión en los cilindros fue desarrollado por el ingeniero de mediados del siglo XIX William Fairbairn , asistido por su analista matemático Eaton Hodgkinson . Su primer interés fue estudiar el diseño y los fallos de las calderas de vapor . ^[9] Fairbairn se dio cuenta de que la tensión circunferencial era el doble de la tensión longitudinal, un factor importante en el montaje de las carcasas de las calderas a partir de láminas laminadas unidas mediante remaches . El trabajo posterior se aplicó a la construcción de puentes y a la invención de la viga cajón . En el puente ferroviario de Chepstow , los pilares de hierro fundido están reforzados por bandas externas de hierro forjado . La fuerza longitudinal vertical es una fuerza de compresión, que el hierro fundido es capaz de resistir. La tensión circunferencial es de tracción, por lo que se añade hierro forjado, un material con mejor resistencia a la tracción que el hierro fundido.

Véase también

• Puede ser causado por la tensión del cilindro:
  • Desastre de la melaza de Boston
  • Explosión de caldera
  • Explosión de vapor en expansión de líquido hirviendo
• Temas de ingeniería relacionados:
  • Concentración de estrés
  • Prueba hidrostática
  • Pandeo
  • Presión arterial#Relación_con_la_tensión_de_la_pared
  • Análisis de tensión en tuberías
• Diseños muy afectados por este estrés:
  • Recipiente a presión
    • Motor de cohete
  • Volante
  • La cúpula de la catedral de Florencia

Referencias

1. "Análisis estructural avanzado" (PDF) . Universidad de Swansea. 2020. pág. 8. Archivado desde el original (PDF) el 19 de agosto de 2019.
2. Harvey, John F. (1974). "Teoría y diseño de recipientes a presión modernos". Van Nostrand Reinhold. págs. 60-61.
3. Tensión en las paredes arteriales Por R Nave. Departamento de Física y Astronomía, Universidad Estatal de Georgia. Consultado en junio de 2011.
4. "Recipiente a presión, aro de pared delgada y ecuaciones de tensiones longitudinales y calculadora - Engineers Edge".
5. "Recipientes a presión" (PDF) . web.mit.edu . Consultado el 12 de junio de 2020 .
6. "Mecánica de materiales - Parte 35 (Cilindro grueso - Ecuación de Lame)". youtube.com . Consultado el 23 de octubre de 2022 .
7. E. Goljan, Patología, 2.ª ed. Mosby Elsevier, Rapid Review Series.
8. Jones, Stephen K. (2009). Brunel en el sur de Gales . Vol. II: Comunicaciones y carbón. Stroud: The History Press. pág. 247. ISBN 9780752449128.
9. Fairbairn, William (1851). "La construcción de calderas". Dos conferencias: La construcción de calderas y Sobre las explosiones de calderas y los medios para prevenirlas. pág. 6.

• Recipientes a presión de paredes delgadas. 19 de junio de 2008. {{cite book}}: |work=ignorado ( ayuda )