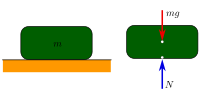
En la mecánica clásica , una partícula está en equilibrio mecánico si la fuerza neta sobre esa partícula es cero. [1] : 39 Por extensión, un sistema físico compuesto de muchas partes está en equilibrio mecánico si la fuerza neta sobre cada una de sus partes individuales es cero. [1] : 45–46 [2]
Además de definir el equilibrio mecánico en términos de fuerza, existen muchas definiciones alternativas de equilibrio mecánico que son todas matemáticamente equivalentes.
De manera más general, en los sistemas conservativos , el equilibrio se establece en un punto en el espacio de configuración donde el gradiente de la energía potencial con respecto a las coordenadas generalizadas es cero.
Si una partícula en equilibrio tiene velocidad cero, esa partícula está en equilibrio estático.. [3] [4] Dado que todas las partículas en equilibrio tienen velocidad constante, siempre es posible encontrar un marco de referencia inercial en el que la partícula esté estacionaria con respecto al marco.
Una propiedad importante de los sistemas en equilibrio mecánico es su estabilidad .
En una función que describe la energía potencial del sistema, los equilibrios del sistema se pueden determinar mediante el cálculo . Un sistema está en equilibrio mecánico en los puntos críticos de la función que describe la energía potencial del sistema. Estos puntos se pueden ubicar utilizando el hecho de que la derivada de la función es cero en estos puntos. Para determinar si el sistema es estable o inestable, se aplica la prueba de la segunda derivada . Al denotar la ecuación estática de movimiento de un sistema con un solo grado de libertad, se pueden realizar los siguientes cálculos:



Al considerar más de una dimensión, es posible obtener resultados diferentes en diferentes direcciones, por ejemplo, estabilidad con respecto a los desplazamientos en la dirección x pero inestabilidad en la dirección y , un caso conocido como punto de silla . Generalmente, un equilibrio solo se considera estable si es estable en todas las direcciones.
En ocasiones, las ecuaciones de equilibrio (condiciones de equilibrio de fuerza y momento) son insuficientes para determinar las fuerzas y reacciones . Esta situación se describe como estáticamente indeterminada .
Las situaciones estáticamente indeterminadas a menudo pueden resolverse utilizando información ajena a las ecuaciones de equilibrio estándar.
Un objeto estacionario (o un conjunto de objetos) se encuentra en "equilibrio estático", que es un caso especial de equilibrio mecánico. Un pisapapeles sobre un escritorio es un ejemplo de equilibrio estático. Otros ejemplos incluyen una escultura de piedra en equilibrio o una pila de bloques en el juego de Jenga , siempre que la escultura o la pila de bloques no estén en estado de colapso .
Los objetos en movimiento también pueden estar en equilibrio. Un niño que se desliza por un tobogán a velocidad constante estaría en equilibrio mecánico, pero no en equilibrio estático (en el marco de referencia de la Tierra o del tobogán).
Otro ejemplo de equilibrio mecánico es el de una persona que presiona un resorte hasta un punto determinado. Puede empujarlo hasta un punto arbitrario y mantenerlo allí, en cuyo punto la carga de compresión y la reacción del resorte son iguales. En este estado, el sistema está en equilibrio mecánico. Cuando se elimina la fuerza de compresión, el resorte vuelve a su estado original.
El número mínimo de equilibrios estáticos de cuerpos homogéneos y convexos (cuando descansan bajo la acción de la gravedad sobre una superficie horizontal) es de especial interés. En el caso plano, el número mínimo es 4, mientras que en tres dimensiones se puede construir un objeto con solo un punto de equilibrio estable y otro inestable. [5] Un objeto de este tipo se denomina gömböc .
{{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace )