Singularidad gravitacional

Condición en la que el espacio-tiempo mismo se descompone

Simulación animada del efecto de lente gravitacional causado por un agujero negro de Schwarzschild que pasa en una línea de visión plana hacia una galaxia de fondo. Alrededor y en el momento de la alineación exacta ( sicigia ) se observa un efecto de lente gravitacional extremo.

Una singularidad gravitacional , singularidad espaciotemporal o simplemente singularidad es una condición en la que se predice que la gravedad será tan intensa que el propio espaciotiempo colapsaría catastróficamente. Como tal, una singularidad, por definición, ya no es parte del espaciotiempo regular y no puede determinarse por "dónde" o "cuándo". Las singularidades gravitacionales existen en una unión entre la relatividad general y la mecánica cuántica ; por lo tanto, las propiedades de la singularidad no pueden describirse sin una teoría establecida de la gravedad cuántica . Tratar de encontrar una definición completa y precisa de las singularidades en la teoría de la relatividad general, la mejor teoría actual de la gravedad, sigue siendo un problema difícil. ^{[1] [2]} Una singularidad en la relatividad general puede definirse por la curvatura invariante escalar que se vuelve infinita ^[3] o, mejor, por una geodésica que es incompleta . ^[4]

Las singularidades gravitacionales se consideran principalmente en el contexto de la relatividad general, donde la densidad se volvería infinita en el centro de un agujero negro sin correcciones de la mecánica cuántica , y dentro de la astrofísica y la cosmología como el estado más temprano del universo durante el Big Bang . Los físicos no han llegado a un consenso sobre lo que realmente sucede en las densidades extremas predichas por las singularidades (incluso al comienzo del Big Bang). ^[5]

La relatividad general predice que cualquier objeto que colapse más allá de un cierto punto (para las estrellas , este es el radio de Schwarzschild ) formaría un agujero negro, dentro del cual se formaría una singularidad (cubierta por un horizonte de sucesos ). ^[2] Los teoremas de singularidad de Penrose-Hawking definen una singularidad como aquella que tiene geodésicas que no se pueden extender de manera suave . ^[6] La terminación de dicha geodésica se considera la singularidad.

La teoría moderna afirma que el estado inicial del universo , al comienzo del Big Bang, era una singularidad. ^[7] En este caso, el universo no colapsó en un agujero negro, porque los cálculos y límites de densidad conocidos actualmente para el colapso gravitacional se basan generalmente en objetos de tamaño relativamente constante, como las estrellas, y no necesariamente se aplican de la misma manera al espacio en rápida expansión como el Big Bang. Ni la relatividad general ni la mecánica cuántica pueden describir actualmente los primeros momentos del Big Bang , ^[8] pero en general, la mecánica cuántica no permite que las partículas habiten un espacio más pequeño que sus longitudes de onda Compton . ^[9]

Interpretación

Muchas teorías de la física tienen singularidades matemáticas de un tipo u otro. Las ecuaciones de estas teorías físicas predicen que la masa de una determinada cantidad se vuelve infinita o aumenta sin límite. Esto suele ser una señal de que falta una pieza en la teoría, como en el caso de la catástrofe ultravioleta , la renormalización y la inestabilidad de un átomo de hidrógeno predichas por la fórmula de Larmor .

En las teorías de campo clásicas, incluida la relatividad especial pero no la relatividad general, se puede decir que una solución tiene una singularidad en un punto particular en el espacio-tiempo donde ciertas propiedades físicas se vuelven imprecisas, y el espacio-tiempo sirve como campo de fondo para localizar la singularidad. Por otro lado, una singularidad en la relatividad general es más compleja porque el espacio-tiempo mismo se vuelve impreciso y la singularidad ya no es parte de la variedad regular del espacio-tiempo. En la relatividad general, una singularidad no puede definirse por "dónde" o "cuándo". ^[10]

Algunas teorías, como la teoría de la gravedad cuántica de bucles , sugieren que las singularidades pueden no existir. ^[11] Esto también es cierto para teorías clásicas de campo unificado como las ecuaciones de Einstein-Maxwell-Dirac. La idea puede enunciarse en la forma de que, debido a los efectos de la gravedad cuántica , existe una distancia mínima más allá de la cual la fuerza de la gravedad ya no continúa aumentando a medida que la distancia entre las masas se acorta, o alternativamente que las ondas de partículas interpenetrantes enmascaran los efectos gravitacionales que se sentirían a distancia.

Motivados por esta filosofía de la gravedad cuántica de bucles, recientemente se ha demostrado ^[12] que tales concepciones pueden realizarse a través de algunas construcciones elementales basadas en el refinamiento del primer axioma de la geometría, a saber, el concepto de punto ^[13] al considerar la prescripción de Klein de dar cuenta de la extensión de un pequeño punto que representa o demuestra un punto, ^[14] que fue una llamada programática que él llamó como una fusión de aritmética y geometría. ^[15] El programa de Klein, según Born, era en realidad una ruta matemática para considerar la "incertidumbre natural en todas las observaciones" mientras se describe "una situación física" por medio de "números reales". ^[16]

Tipos

Solo existe un tipo de singularidad, cada una con diferentes características físicas que tienen características relevantes para las teorías de las que surgieron originalmente, como las diferentes formas de las singularidades, cónicas y curvas . También se ha planteado la hipótesis de que ocurren sin horizontes de eventos, estructuras que delimitan una sección del espacio-tiempo de otra en la que los eventos no pueden afectar más allá del horizonte; estas se denominan desnudas.

Cónico

Una singularidad cónica ocurre cuando hay un punto en el que el límite de alguna cantidad invariante del difeomorfismo no existe o es infinito, en cuyo caso el espacio-tiempo no es uniforme en el punto del límite mismo. Por lo tanto, el espacio-tiempo parece un cono alrededor de este punto, donde la singularidad se encuentra en la punta del cono. La métrica puede ser finita en cualquier lugar en el que se utilice el sistema de coordenadas .

Un ejemplo de tal singularidad cónica es una cuerda cósmica y un agujero negro de Schwarzschild . ^[17]

Curvatura

Una ilustración sencilla de un agujero negro que no gira y su singularidad.

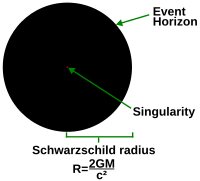
Las soluciones a las ecuaciones de la relatividad general o a otra teoría de la gravedad (como la supergravedad ) a menudo dan como resultado puntos en los que la métrica explota hasta el infinito. Sin embargo, muchos de estos puntos son completamente regulares , y los infinitos son simplemente el resultado de usar un sistema de coordenadas inadecuado en este punto . Para comprobar si hay una singularidad en un punto determinado, se debe comprobar si en este punto las cantidades invariantes del difeomorfismo (es decir, los escalares ) se vuelven infinitas. Tales cantidades son las mismas en todos los sistemas de coordenadas, por lo que estos infinitos no "desaparecerán" con un cambio de coordenadas.

Un ejemplo es la solución de Schwarzschild que describe un agujero negro no rotatorio y sin carga . En sistemas de coordenadas convenientes para trabajar en regiones alejadas del agujero negro, una parte de la métrica se vuelve infinita en el horizonte de sucesos . Sin embargo, el espacio-tiempo en el horizonte de sucesos es regular . La regularidad se hace evidente al cambiar a otro sistema de coordenadas (como las coordenadas de Kruskal ), donde la métrica es perfectamente suave . Por otro lado, en el centro del agujero negro, donde la métrica también se vuelve infinita, las soluciones sugieren que existe una singularidad. La existencia de la singularidad se puede verificar notando que el escalar de Kretschmann , al ser el cuadrado del tensor de Riemann , es decir , que es invariante al difeomorfismo, es infinito. ${\displaystyle R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }}$

Mientras que en un agujero negro que no gira la singularidad se produce en un único punto de las coordenadas del modelo, denominado "singularidad puntual", en un agujero negro que gira, también conocido como agujero negro de Kerr , la singularidad se produce en un anillo (una línea circular), conocido como " singularidad de anillo ". Una singularidad de este tipo también puede, en teoría, convertirse en un agujero de gusano . ^[18]

En términos más generales, un espacio-tiempo se considera singular si es geodésicamente incompleto , lo que significa que hay partículas en caída libre cuyo movimiento no se puede determinar más allá de un tiempo finito, es decir, después del punto de alcanzar la singularidad. Por ejemplo, cualquier observador dentro del horizonte de sucesos de un agujero negro que no gira caería en su centro dentro de un período finito de tiempo. La versión clásica del modelo cosmológico del Big Bang del universo contiene una singularidad causal al comienzo del tiempo ( t = 0), donde todas las geodésicas temporales no tienen extensiones hacia el pasado. Extrapolando hacia atrás a este tiempo hipotético 0, se obtiene un universo con todas las dimensiones espaciales de tamaño cero, densidad infinita, temperatura infinita y curvatura espacio-temporal infinita.

Singularidad desnuda

Hasta principios de los años 1990, se creía ampliamente que la relatividad general oculta cada singularidad detrás de un horizonte de sucesos , lo que hace imposible la existencia de singularidades desnudas. Esto se conoce como la hipótesis de la censura cósmica . Sin embargo, en 1991, los físicos Stuart Shapiro y Saul Teukolsky realizaron simulaciones por computadora de un plano de polvo giratorio que indicaron que la relatividad general podría permitir la existencia de singularidades "desnudas". Se desconoce cómo se verían realmente estos objetos en un modelo de este tipo. Tampoco se sabe si seguirían surgiendo singularidades si se eliminaran los supuestos simplificadores utilizados para realizar la simulación. Sin embargo, se plantea la hipótesis de que la luz que entra en una singularidad también vería terminadas sus geodésicas, lo que haría que la singularidad desnuda pareciera un agujero negro. ^{[19] [20] [21]}

Los horizontes de eventos que desaparecen existen en la  métrica de Kerr , que es un agujero negro giratorio en el vacío, si el  momento angular  ( ) es lo suficientemente alto. Transformando la métrica de Kerr a  coordenadas de Boyer–Lindquist , se puede demostrar ^[22]  que la coordenada (que no es el radio) del horizonte de eventos es, , donde  , y  . En este caso, "los horizontes de eventos desaparecen" significa cuando las soluciones son complejas para  , o  . Sin embargo, esto corresponde a un caso donde excede (o en unidades de Planck , ) ; es decir, el espín excede lo que normalmente se considera como el límite superior de sus valores físicamente posibles. ${\displaystyle J}$ ${\displaystyle r_{\pm }=\mu \pm \left(\mu ^{2}-a^{2}\right)^{1/2}}$ ${\displaystyle \mu =GM/c^{2}}$ ${\displaystyle a=J/Mc}$ ${\displaystyle r_{\pm }}$ ${\displaystyle \mu ^{2}<a^{2}}$ ${\displaystyle J}$ ${\displaystyle GM^{2}/c}$ ${\displaystyle J>M^{2}}$

De manera similar, la desaparición de horizontes de eventos también se puede ver con la  geometría de Reissner-Nordström  de un agujero negro cargado si la carga ( ) es lo suficientemente alta. En esta métrica, se puede demostrar ^[23]  que las singularidades ocurren en , donde  , y  . De los tres casos posibles para los valores relativos de  y  , el caso donde   hace que ambos  sean complejos. Esto significa que la métrica es regular para todos los valores positivos de  , o en otras palabras, la singularidad no tiene horizonte de eventos. Sin embargo, esto corresponde a un caso donde excede (o en unidades de Planck, ) ; es decir, la carga excede lo que normalmente se considera el límite superior de sus valores físicamente posibles. Además, no se espera que los agujeros negros astrofísicos reales posean ninguna carga apreciable. ${\displaystyle Q}$ ${\displaystyle r_{\pm }=\mu \pm \left(\mu ^{2}-q^{2}\right)^{1/2}}$ ${\displaystyle \mu =GM/c^{2}}$ ${\displaystyle q^{2}=GQ^{2}/\left(4\pi \epsilon _{0}c^{4}\right)}$ ${\displaystyle \mu }$ ${\displaystyle q}$ ${\displaystyle \mu ^{2}<q^{2}}$ ${\displaystyle r_{\pm }}$ ${\displaystyle r}$ ${\displaystyle Q/{\sqrt {4\pi \epsilon _{0}}}}$ ${\displaystyle M{\sqrt {G}}}$ ${\displaystyle Q>M}$

Un agujero negro que posee el valor más bajo consistente con sus valores y y los límites señalados anteriormente, es decir, uno justo en el punto de perder su horizonte de eventos, se denomina extremal . ${\displaystyle M}$ ${\displaystyle J}$ ${\displaystyle Q}$

Entropía

Antes de que Stephen Hawking propusiera el concepto de radiación de Hawking , se había evitado la cuestión de si los agujeros negros tenían entropía. Sin embargo, este concepto demuestra que los agujeros negros irradian energía, lo que conserva la entropía y resuelve los problemas de incompatibilidad con la segunda ley de la termodinámica . Sin embargo, la entropía implica calor y, por lo tanto, temperatura. La pérdida de energía también implica que los agujeros negros no duran para siempre, sino que se evaporan o decaen lentamente. La temperatura del agujero negro está inversamente relacionada con la masa . ^[24] Todos los candidatos conocidos a agujero negro son tan grandes que su temperatura está muy por debajo de la de la radiación cósmica de fondo, lo que significa que ganarán energía en términos netos al absorber esta radiación. No pueden comenzar a perder energía en términos netos hasta que la temperatura de fondo caiga por debajo de su propia temperatura. Esto ocurrirá en un corrimiento al rojo cosmológico de más de un millón, en lugar de los mil o más desde que se formó la radiación de fondo. ^{[ cita requerida ]}

Véase también

• Singularidad de dimensión 0: monopolo magnético
• Singularidad unidimensional: cuerda cósmica
• Singularidad bidimensional: pared de dominio
• Fuzzball (teoría de cuerdas)
• Teoremas de singularidad de Penrose-Hawking
• Agujero blanco
• Singularidad BKL
• Singularidad inicial

Referencias

1. Earman 1995, Sección 2.2 ¿Qué es una singularidad? p.28-31
2. Curiel, Erik (2021). «Singularidades y agujeros negros». Stanford Encyclopedia of Philosophy . Metaphysics Research Lab, Stanford University . Consultado el 1 de octubre de 2021 .
3. "Singularidades". Física del Universo .
4. Uggla, Claes (2006). «Singularidades del espacio-tiempo». Einstein Online . 2 (1002). Instituto Max Planck de Física Gravitacional . Archivado desde el original el 24 de enero de 2017 . Consultado el 20 de octubre de 2015 .
5. Earman 1995, Capítulo 8 "Epílogo"
6. Moulay, Emmanuel. "El universo y los fotones" (PDF) . FQXi Foundational Questions Institute . Consultado el 26 de diciembre de 2012 .
7. Wald 1984, pág. 99
8. Hawking, Stephen. «El comienzo del tiempo». Stephen Hawking: sitio web oficial . Universidad de Cambridge . Archivado desde el original el 6 de octubre de 2014. Consultado el 26 de diciembre de 2012 .
9. Zebrowski, Ernest (2000). Una historia del círculo: razonamiento matemático y el universo físico. Piscataway, Nueva Jersey: Rutgers University Press . pág. 180. ISBN 978-0813528984.
10. Ashtekar, Abhay (2005). "3: "La naturaleza de las singularidades del espacio-tiempo" por Alan D. Randall". En Ashtekar, Abhay (ed.). 100 años de relatividad: estructura del espacio-tiempo, Einstein y más allá . Singapur: World Scientific. ISBN 978-981-256-394-1.
11. Gambini, Rodolfo; Olmedo, Javier; Pullin, Jorge (7 de mayo de 2014). "Agujeros negros cuánticos en gravedad cuántica de bucles". Gravedad clásica y cuántica . 31 (9): 095009. arXiv : 1310.5996 . Bibcode :2014CQGra..31i5009G. doi :10.1088/0264-9381/31/9/095009. ISSN  0264-9381. S2CID  : 119247455.{{cite journal}}: CS1 maint: date and year (link)
12. Majhi, Abhishek (2022). "Resolver la singularidad observando el punto y demostrar la indecidibilidad de la hipótesis del continuo". Fundamentos de la ciencia . 29 (2): 405–440. doi :10.1007/s10699-022-09875-9. ISSN  1233-1821. S2CID  246942045.
13. Euclides; Heiberg, JL; Fitzpatrick, R. (2008). Fitzpatrick, Richard (ed.). Elementos de geometría de Euclides: el texto griego de JL Heiberg (1883 - 1885): de Euclidis Elementa, editit et Latine interpretatus est IL Heiberg, in aedibus BG Teubneri, 1883-1885 (PDF) . Traducido por Fitzpatrick, Richard (Ed. revisada y corregida). ISBN​ 978-0-615-17984-1.
14. Klein, Felix (2016). Matemáticas elementales desde un punto de vista superior . Springer Berlin Heidelberg. ISBN 978-3662495155.
15. Klein, Felix (2011). Conferencias sobre matemáticas dictadas en el Coloquio de Evanston del 28 de agosto al 9 de septiembre de 1893 ante los miembros del Congreso de Matemáticas celebrado en relación con la Feria Mundial de Chicago (PDF) . El Proyecto Gutenberg.
16. Nacido, Max (1968). Física en mi generación . Springer Nueva York.
17. Copeland, Edmund J; Myers, Robert C; Polchinski, Joseph (2004). "Cuerdas F y D cósmicas". Journal of High Energy Physics . 2004 (6): 013. arXiv : hep-th/0312067 . Código Bibliográfico :2004JHEP...06..013C. doi :10.1088/1126-6708/2004/06/013. S2CID  140465.
18. Si se aplica una carga eléctrica uniforme a una singularidad rotatoria, se genera una fuerza repelente que provoca la formación de una singularidad en anillo . El efecto puede ser un agujero de gusano estable , una perforación no puntual en el espacio-tiempo que puede estar conectada a una segunda singularidad en anillo en el otro extremo. Aunque a menudo se sugieren estos agujeros de gusano como rutas para viajar a velocidades superiores a la de la luz, tales sugerencias ignoran el problema de escapar del agujero negro en el otro extremo, o incluso de sobrevivir a las inmensas fuerzas de marea en el interior fuertemente curvado del agujero de gusano.
19. Bojowald, Martin (2008). "Cosmología cuántica de bucles". Living Reviews in Relativity . 11 (1): 4. Bibcode :2008LRR....11....4B. doi : 10.12942/lrr-2008-4 . ISSN  2367-3613. PMC 5255532 . PMID  28163606. 
20. Goswami, Rituparno; Joshi, Pankaj S. (2008). "Colapso gravitacional esférico en N dimensiones". Revisión física D. 76 (8): 084026. arXiv : gr-qc/0608136 . Código Bib : 2007PhRvD..76h4026G. doi : 10.1103/PhysRevD.76.084026. ISSN  1550-7998. S2CID  119441682.
21. Goswami, Rituparno; Joshi, Pankaj S.; Singh, Parampreet (27 de enero de 2006). "Evaporación cuántica de una singularidad desnuda". Physical Review Letters . 96 (3): 031302. arXiv : gr-qc/0506129 . Código Bibliográfico :2006PhRvL..96c1302G. doi :10.1103/PhysRevLett.96.031302. ISSN  0031-9007. PMID  16486681. S2CID  19851285.{{cite journal}}: CS1 maint: date and year (link)
22. Hobson, Efstathiou y Lasenby 2013, págs. 300–305
23. Hobson, Efstathiou y Lasenby 2013, págs. 320–325
24. LoPresto, MC (2003). "Algunas termodinámicas simples de agujeros negros". The Physics Teacher . 41 (5): 299–301. Código Bibliográfico :2003PhTea..41..299L. doi :10.1119/1.1571268. S2CID  122758428.

Bibliografía

• Earman, John (1995). Golpes, crujidos, gemidos y chillidos: singularidades y acausalidades en los espacio-tiempos relativistas . Oxford University Press. ISBN 019509591X.
• Joshi, Pankaj S (2007). Colapso gravitacional y singularidades del espacio-tiempo . Nueva York: Cambridge University Press. ISBN 9781107405363.
• Misner, Charles W .; Thorne, Kip ; Wheeler, John Archibald (1973). Gravitación . WH Freeman . ISBN 0-7167-0344-0.§31.2 La no singularidad del radio gravitacional y secciones siguientes; §34 Técnicas globales, horizontes y teoremas de singularidad
• Wald, Robert M. (1984). Relatividad general . University of Chicago Press . ISBN 0-226-87033-2.
• Hawking, SW ; Penrose, R. (1970). "Las singularidades del colapso gravitacional y la cosmología". Actas de la Royal Society de Londres. A. Ciencias Físicas y Matemáticas . 314 (1519): 529–548. Bibcode :1970RSPSA.314..529H. doi : 10.1098/rspa.1970.0021 . ISSN  0080-4630.
• Shapiro, Stuart L.; Teukolsky, Saul A. (1991). "Formación de singularidades desnudas: La violación de la censura cósmica". Physical Review Letters . 66 (8): 994–997. Bibcode :1991PhRvL..66..994S. doi :10.1103/PhysRevLett.66.994. ISSN  0031-9007. PMID  10043968. S2CID  7830407.
• Penrose, Roger (diciembre de 1996). "Chandrasekhar, agujeros negros y singularidades" (PDF) . Revista de Astrofísica y Astronomía . 17 (3–4): 213–231. doi :10.1007/BF02702305. ISSN  0250-6335.
• Penrose, Roger (diciembre de 1999). "La cuestión de la censura cósmica" (PDF) . Revista de Astrofísica y Astronomía . 20 (3–4): 233–248. doi :10.1007/BF02702355. ISSN  0250-6335.
• Singh, TP (diciembre de 1999). "Colapso gravitacional, agujeros negros y singularidades desnudas" (PDF) . Revista de Astrofísica y Astronomía . 20 (3–4): 221–232. doi :10.1007/BF02702354. ISSN  0250-6335.
• Hobson, Michael P.; Efstathiou, George; Lasenby, Anthony (2013). Relatividad general: una introducción para físicos (1.ª edición, 6.ª edición impresa). Cambridge: Cambridge University Press. ISBN 978-0-521-82951-9.

Lectura adicional

• El universo elegante de Brian Greene . Este libro ofrece una introducción a la teoría de cuerdas para el público en general , aunque algunas de las opiniones expresadas ya están quedando obsoletas. Su uso de términos comunes y la provisión de ejemplos a lo largo del texto ayudan al público en general a comprender los conceptos básicos de la teoría de cuerdas.