Cinco puntos determinan una cónica.

Principio en geometría

En geometría euclidiana y proyectiva , cinco puntos determinan una cónica (una curva plana de grado 2), del mismo modo que dos puntos (distintos) determinan una línea (una curva plana de grado 1 ). Hay sutilezas adicionales para las cónicas que no existen para las líneas y, por lo tanto, el enunciado y su demostración para las cónicas son más técnicos que para las líneas.

Formalmente, dados cinco puntos cualesquiera en el plano en posición lineal general , es decir, no hay tres colineales , hay una cónica única que pasa a través de ellos, que no será degenerada ; esto es cierto tanto en el plano euclidiano como en cualquier plano proyectivo papio . De hecho, dados cinco puntos cualesquiera, hay una cónica que los atraviesa, pero si tres de los puntos son colineales, la cónica será degenerada (reducible, porque contiene una línea) y puede no ser única; ver más discusión .

Pruebas

Este resultado se puede demostrar de muchas maneras diferentes; el argumento del recuento de dimensiones es más directo y se generaliza en mayor grado, mientras que otras pruebas son especiales para las cónicas.

Conteo de dimensiones

Intuitivamente, pasar por cinco puntos en una posición lineal general especifica cinco restricciones lineales independientes en el espacio lineal (proyectivo) de las cónicas y, por tanto, especifica una cónica única, aunque esta breve afirmación ignora las sutilezas.

Más precisamente, esto se ve de la siguiente manera:

• Las cónicas corresponden a puntos en el espacio proyectivo de cinco dimensiones. ${\displaystyle \mathbf {P} ^{5};}$
• requerir que una cónica pase por un punto impone una condición lineal en las coordenadas: para un fijo la ecuación es una ecuación lineal en ${\displaystyle (x,y),}$ ${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0}$ ${\displaystyle (A,B,C,D,E,F);}$
• mediante el conteo de dimensiones , se necesitan cinco restricciones (que la curva pase por cinco puntos) para especificar una cónica, ya que cada restricción corta la dimensión de posibilidades en 1 y se comienza con 5 dimensiones;
• en 5 dimensiones, la intersección de 5 hiperplanos (independientes) es un solo punto (formalmente, según el teorema de Bézout );
• la posición lineal general de los puntos significa que las restricciones son independientes y, por tanto, especifican una cónica única;
• la cónica resultante no es degenerada porque es una curva (ya que tiene más de 1 punto) y no contiene una línea (de lo contrario, se dividiría en dos líneas, al menos una de las cuales debe contener 3 de los 5 puntos). por el principio del casillero ), por lo que es irreducible.

Las dos sutilezas del análisis anterior son que el punto resultante es una ecuación cuadrática (no una ecuación lineal) y que las restricciones son independientes. La primera es simple: si A , B y C desaparecen, entonces la ecuación define una línea, y 3 puntos cualesquiera de esta (de hecho, cualquier número de puntos) se encuentran en una línea; por lo tanto, la posición lineal general garantiza una cónica. La segunda, que las restricciones son independientes, es significativamente más sutil: corresponde al hecho de que dados cinco puntos en posición lineal general en el plano, sus imágenes bajo el mapa de Veronese están en posición lineal general, lo cual es cierto porque el mapa de Veronese es biregular : es decir, si la imagen de cinco puntos satisface una relación, entonces la relación puede retroceder y los puntos originales también deben satisfacer una relación. El mapa de Veronese tiene coordenadas y el objetivo es dual al de las cónicas. El mapa de Veronese corresponde a la "evaluación de una cónica en un punto", y la afirmación sobre la independencia de las restricciones es exactamente una declaración geométrica sobre este mapa. ${\displaystyle Dx+Ey+F=0}$ ${\displaystyle \mathbf {P} ^{5}}$ ${\displaystyle [x^{2}:xy:y^{2}:xz:yz:z^{2}],}$ ${\displaystyle \mathbf {P} ^{5}}$ ${\displaystyle [A:B:C:D:E:F]}$ ${\displaystyle \mathbf {P} ^{5}}$

Prueba sintética

Que cinco puntos determinan una cónica puede demostrarse mediante geometría sintética , es decir, en términos de líneas y puntos en el plano, además de la prueba analítica (algebraica) dada anteriormente. Tal prueba se puede dar utilizando un teorema de Jakob Steiner , ^[1] que establece:

Dada una transformación proyectiva f, entre el lápiz de líneas que pasan por un punto X y el lápiz de líneas que pasan por un punto Y, el conjunto C de puntos de intersección entre una línea x y su imagen forma una cónica. ${\displaystyle f(x)}$

Tenga en cuenta que X e Y están en esta cónica al considerar la preimagen y la imagen de la línea XY (que es respectivamente una línea que pasa por X y una línea que pasa por Y ).

Esto se puede demostrar tomando los puntos X e Y como puntos estándar y mediante una transformación proyectiva, en cuyo caso los lápices de líneas corresponden a las líneas horizontales y verticales en el plano, y las intersecciones de las líneas correspondientes a la gráfica de un función, que (debe mostrarse) es una hipérbola, por lo tanto una cónica, por lo tanto la curva original C es una cónica. ${\displaystyle [1:0:0]}$ ${\displaystyle [0:1:0]}$

Ahora, dados cinco puntos X, Y, A, B, C, las tres líneas pueden llevarse a las tres líneas mediante una transformación proyectiva única, ya que las transformaciones proyectivas son simplemente 3-transitivas en líneas (son simplemente 3-transitivas en puntos, de ahí que por dualidad proyectiva sean 3-transitivos en líneas). Bajo este mapa, X se asigna a Y, ya que estos son los únicos puntos de intersección de estas líneas y, por lo tanto, satisfacen la hipótesis del teorema de Steiner. La cónica resultante contiene así los cinco puntos y es la única cónica que se desee. ${\displaystyle XA,XB,XC}$ ${\displaystyle YA,YB,YC}$

Construcción de parábola, dados cinco puntos.

Construcción

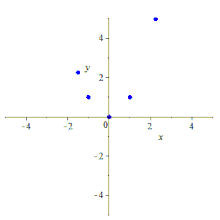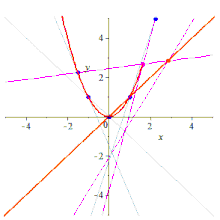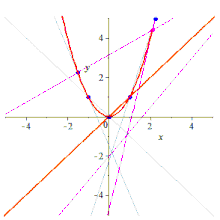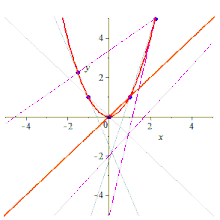
Dados cinco puntos, se puede construir la cónica que los contiene de varias maneras.

Analíticamente, dadas las coordenadas de los cinco puntos, la ecuación de la cónica se puede encontrar mediante álgebra lineal , escribiendo y resolviendo las cinco ecuaciones en los coeficientes, sustituyendo las variables por los valores de las coordenadas: cinco ecuaciones, seis incógnitas, pero homogéneo, por lo que al escalarlo se elimina una dimensión; concretamente, establecer uno de los coeficientes en 1 logra esto. ${\displaystyle (x_{i},y_{i})_{i=1,2,3,4,5}}$

Esto se puede lograr de manera bastante directa como la siguiente ecuación determinante:

${\displaystyle \det {\begin{bmatrix}x^{2}&xy&y^{2}&x&y&1\\x_{1}^{2}&x_{1}y_{1}&y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}&x_{2}y_{2}&y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}&x_{3}y_{3}&y_{3}^{2}&x_{3}&y_{3}&1\\x_{4}^{2}&x_{4}y_{4}&y_{4}^{2}&x_{4}&y_{4}&1\\x_{5}^{2}&x_{5}y_{5}&y_{5}^{2}&x_{5}&y_{5}&1\end{bmatrix}}=0}$

Esta matriz tiene variables en su primera fila y números en todas las demás filas, por lo que el determinante es visiblemente una combinación lineal de los seis monomios de grado 2 como máximo. Además, el polinomio resultante claramente se desvanece en los cinco puntos de entrada (cuando ), como la matriz tiene entonces una fila repetida. ${\displaystyle (x,y)=(x_{i},y_{i})}$

Sintéticamente, la cónica se puede construir mediante laConstrucción de Braikenridge-Maclaurin ,^[2][3][4][5]aplicando elteorema de Braikenridge-Maclaurin, que es el inverso delteorema de Pascal. El teorema de Pascal establece que dados6puntos en una cónica (un hexágono), las rectas definidas por lados opuestos se cruzan en tres puntos colineales. Esto se puede revertir para construir las posibles ubicaciones para un sexto punto, dados los 5 existentes.

Generalizaciones

La generalización natural es preguntar para qué valor de k una configuración de k puntos (en posición general) en el espacio n determina una variedad de grado d y dimensión m , lo cual es una cuestión fundamental en geometría enumerativa .

Un caso simple de esto es el de una hipersuperficie (una subvariedad de codimensión 1, los ceros de un solo polinomio, el caso ), de la cual las curvas planas son un ejemplo. ${\displaystyle m=n-1}$

En el caso de una hipersuperficie, la respuesta se da en términos del coeficiente multiconjunto , más familiarmente el coeficiente binomial , o más elegantemente el factorial ascendente , como:

${\displaystyle k=\left(\!\!{n+1 \choose d}\!\!\right)-1={n+d \choose d}-1={\frac {1}{n!}}(d+1)^{(n)}-1.}$

Esto se realiza a través del análisis análogo del mapa de Veronese : k puntos en posición general imponen k condiciones lineales independientes en una variedad (porque el mapa de Veronese es biregular), y el número de monomios de grado d en variables ( espacio proyectivo n -dimensional tiene coordenadas homogéneas) es del cual se resta 1 debido a la proyectivización: multiplicar un polinomio por una constante no cambia sus ceros. ${\displaystyle n+1}$ ${\displaystyle n+1}$ ${\displaystyle \textstyle {\left(\!\!{n+1 \choose d}\!\!\right)},}$

En la fórmula anterior, el número de puntos k es un polinomio en d de grado n, con coeficiente principal ${\displaystyle 1/n!}$

En el caso de curvas planas, donde la fórmula queda: ${\displaystyle n=2,}$

${\displaystyle \textstyle {\frac {1}{2}}(d+1)(d+2)-1=\textstyle {\frac {1}{2}}(d^{2}+3d)}$

cuyos valores para son : no hay curvas de grado 0 (un solo punto es un punto y por lo tanto está determinado por un punto, que es codimensión 2), 2 puntos determinan una línea, 5 puntos determinan una cónica, 9 puntos determinan una cúbica , 14 puntos determinan una cuarta, y así sucesivamente. ${\displaystyle d=0,1,2,3,4}$ ${\displaystyle 0,2,5,9,14}$

Resultados relacionados

Si bien cinco puntos determinan una cónica, los conjuntos de seis o más puntos de una cónica no están en posición general, es decir, están restringidos como se demuestra en el teorema de Pascal .

De manera similar, si bien nueve puntos determinan una cúbica, si los nueve puntos se encuentran en más de una cúbica (es decir, son la intersección de dos cúbicas), entonces no están en posición general y, de hecho, satisfacen una restricción de suma, como se establece en Cayley. –Teorema de Bacharach .

Cuatro puntos no determinan una cónica, sino más bien un lápiz , el sistema lineal unidimensional de cónicas que pasan por los cuatro puntos (formalmente, tienen los cuatro puntos como lugar base ). De manera similar, tres puntos determinan un sistema lineal bidimensional (red), dos puntos determinan un sistema lineal tridimensional (red), un punto determina un sistema lineal de 4 dimensiones y cero puntos no imponen restricciones al sistema lineal de 5 dimensiones. sistema de todas las cónicas.

Los círculos apolíneos son dos familias de 1 parámetro determinadas por 2 puntos.

Como es bien sabido, tres puntos no colineales determinan un círculo en la geometría euclidiana y dos puntos distintos determinan un lápiz de círculos como los círculos apolíneos . Estos resultados parecen ir en contra del resultado general, ya que los círculos son casos especiales de cónicas. Sin embargo, en un plano proyectivo papio una cónica es un círculo sólo si pasa por dos puntos específicos de la recta del infinito , por lo que un círculo está determinado por cinco puntos no colineales, tres en el plano afín y estos dos puntos especiales. Consideraciones similares explican el número menor de puntos necesarios para definir los lápices de círculos.

Tangencia

En lugar de pasar por puntos, una condición diferente en una curva es ser tangente a una línea determinada. Ser tangente a cinco rectas dadas también determina una cónica, por dualidad proyectiva , pero desde el punto de vista algebraico la tangencia a una recta es una restricción cuadrática , por lo que el conteo ingenuo de dimensiones produce 2 ^{· 5}  = 32 cónicas tangentes a cinco rectas dadas, de las cuales 31 debe atribuirse a cónicas degeneradas, como se describe en factores de manipulación en geometría enumerativa ; Formalizar esta intuición requiere un desarrollo adicional significativo para justificarla.

Otro problema clásico de la geometría enumerativa, de estilo similar al de las cónicas, es el Problema de Apolonio : un círculo tangente a tres círculos en general determina ocho círculos, ya que cada uno de ellos es una condición cuadrática y 2 ^{· 3}  = 8. Como pregunta En geometría real, un análisis completo implica muchos casos especiales, y el número real de círculos puede ser cualquier número entre 0 y 8, excepto 7.

Ver también

• Teorema de Cramer (curvas algebraicas) , para una generalización a curvas planas de n -ésimo grado

Referencias

1. Curso interactivo sobre geometría proyectiva Archivado el 27 de noviembre de 2017 en Wayback Machine , Capítulo cinco: La geometría proyectiva de las cónicas Archivado el 22 de diciembre de 2017 en Wayback Machine : Sección cuatro: Cónicas en el plano proyectivo real Archivado el 4 de 2018 24 en la Wayback Machine , de JC Álvarez Paiva; la prueba sigue el ejercicio 4.6
2. (Coxeter 1961, págs. 252-254)
3. El Pascal animado, Sandra Lach Arlinghaus
4. Weisstein, Eric W. "Construcción Braikenridge-Maclaurin". De MathWorld: un recurso web de Wolfram. http://mathworld.wolfram.com/Braikenridge-MaclaurinConstruction.html
5. La página de secciones cónicas de GNU 3DLDF: el teorema de Pascal y la construcción de Braikenridge-Maclaurin, Laurence D. Finston

• Coxeter, HSM (1961), Introducción a la geometría , Washington, DC{{citation}}: CS1 maint: location missing publisher (link)
• Coxeter, HSM ; Greitzer, SL (1967), Geometry Revisited , Washington, DC: Asociación Matemática de América , p. 76
• Dixon, AC (marzo de 1908), "La cónica a través de cinco puntos dados", The Mathematical Gazette , 4 (70), The Mathematical Association: 228–230, doi :10.2307/3605147, JSTOR  3605147, S2CID  125356690

enlaces externos

• Cinco puntos determinan una sección cónica, demostración interactiva de Wolfram