
En economía , los rendimientos decrecientes son la disminución de la producción marginal (incremental) de un proceso de producción a medida que la cantidad de un solo factor de producción aumenta de forma incremental, manteniendo todos los demás factores de producción iguales ( ceteris paribus ). [1] La ley de rendimientos decrecientes (también conocida como ley de productividad marginal decreciente) establece que en los procesos productivos, aumentar un factor de producción en una unidad, mientras se mantienen constantes todos los demás factores de producción, en algún momento arrojará una unidad menor de producción por unidad incremental de insumo. [2] [3] La ley de rendimientos decrecientes no causa una disminución en las capacidades de producción generales, sino que define un punto en una curva de producción mediante el cual producir una unidad adicional de producción resultará en una pérdida y se conoce como rendimientos negativos. Con rendimientos decrecientes, la producción sigue siendo positiva, pero la productividad y la eficiencia disminuyen.
La comprensión moderna de la ley añade la dimensión de mantener iguales los demás resultados, ya que se entiende que un proceso dado puede producir coproductos. [4] Un ejemplo sería una fábrica que aumenta su producto vendible, pero también aumenta su producción de CO 2 , para el mismo aumento de insumos. [2] La ley de rendimientos decrecientes es un principio fundamental tanto de la micro como de la macroeconomía y desempeña un papel central en la teoría de la producción . [5]
El concepto de rendimientos decrecientes se puede explicar considerando otras teorías como el concepto de crecimiento exponencial . [6] Se entiende comúnmente que el crecimiento no continuará aumentando exponencialmente, sino que está sujeto a diferentes formas de restricciones como la disponibilidad limitada de recursos y capitalización que pueden causar estancamiento económico . [7] Este ejemplo de producción es válido para este entendimiento común ya que la producción está sujeta a los cuatro factores de producción que son tierra, trabajo, capital y empresa. [8] Estos factores tienen la capacidad de influir en el crecimiento económico y eventualmente pueden limitar o inhibir el crecimiento exponencial continuo. [9] Por lo tanto, como resultado de estas restricciones, el proceso de producción eventualmente alcanzará un punto de rendimiento máximo en la curva de producción y aquí es donde la producción marginal se estancará y se moverá hacia cero. [10] La innovación en forma de avances tecnológicos o progreso gerencial puede minimizar o eliminar los rendimientos decrecientes para restaurar la productividad y la eficiencia y generar ganancias. [11]
Esta idea puede entenderse fuera de la teoría económica, por ejemplo, en el caso de la población. El tamaño de la población de la Tierra está creciendo rápidamente, pero esto no continuará para siempre (exponencialmente). Las limitaciones, como los recursos, harán que el crecimiento de la población se estanque en algún momento y comience a disminuir. [6] De manera similar, comenzará a disminuir hacia cero, pero no llegará a ser un valor negativo, la misma idea que en la tasa de rendimiento decreciente inevitable para el proceso de producción.
El concepto de rendimientos decrecientes se remonta a las preocupaciones de los primeros economistas como Johann Heinrich von Thünen , Jacques Turgot , Adam Smith , [12] James Steuart , Thomas Robert Malthus y [13] David Ricardo . La ley de los rendimientos decrecientes se remonta al siglo XVIII, en el trabajo de Jacques Turgot. Argumentó que "cada aumento [en un insumo] sería cada vez menos productivo". [14] En 1815, David Ricardo, Thomas Malthus, Edward West y Robert Torrens aplicaron el concepto de rendimientos decrecientes a la renta de la tierra. Estos trabajos fueron relevantes para los comités del Parlamento en Inglaterra, que estaban investigando por qué los precios de los granos eran tan altos y cómo reducirlos. Los cuatro economistas concluyeron que los precios de los productos habían aumentado debido a las Guerras napoleónicas , que afectaron al comercio internacional y provocaron que los agricultores se mudaran a tierras que no estaban desarrolladas y estaban más alejadas. Además, al final de las guerras napoleónicas, se restablecieron las importaciones de cereales, lo que provocó una caída de los precios porque los agricultores necesitaban atraer clientes y vender sus productos más rápido. [15]
Los economistas clásicos, como Malthus y Ricardo, atribuyeron la disminución sucesiva de la producción a la disminución de la calidad de los insumos, mientras que los economistas neoclásicos suponen que cada "unidad" de trabajo es idéntica. Los rendimientos decrecientes se deben a la interrupción de todo el proceso de producción a medida que se agregan unidades adicionales de trabajo a una cantidad fija de capital. La ley de los rendimientos decrecientes sigue siendo una consideración importante en áreas de producción como la agricultura y la ganadería.
Propuesta en el umbral de la Primera Revolución Industrial , se basó en la idea de que se trataba de un producto único. En los últimos años, desde la década de 1970, los economistas han tratado de redefinir la teoría para hacerla más apropiada y relevante en las sociedades económicas modernas. [4] En concreto, analiza qué supuestos se pueden hacer con respecto a la cantidad de insumos, la calidad, la sustitución y los productos complementarios, y la coproducción, cantidad y calidad de los productos.
El origen de la ley de los rendimientos decrecientes se desarrolló principalmente en el sector agrícola. A principios del siglo XIX, David Ricardo, así como otros economistas ingleses mencionados anteriormente, adoptaron esta ley como resultado de la experiencia vivida en Inglaterra después de la guerra. Se desarrolló observando la relación entre los precios del trigo y el maíz y la calidad de la tierra que producía las cosechas. [16] La observación fue que, en un momento determinado, la calidad de la tierra seguía aumentando, pero también lo hacía el costo de los productos, etc. Por lo tanto, cada unidad adicional de trabajo en los campos agrícolas, en realidad proporcionaba un rendimiento decreciente o marginalmente decreciente. [17]

Un ejemplo común de rendimientos decrecientes es optar por contratar más personas en una planta de producción para modificar las capacidades de producción y fabricación actuales. Dado que el capital en la planta (por ejemplo, máquinas de fabricación, tecnología preexistente, almacenes) se mantiene constante, aumentar de un empleado a dos empleados equivale, en teoría, a duplicar las posibilidades de producción y esto se denomina rendimientos crecientes.
Si se emplean 50 personas, en algún momento, aumentar el número de empleados en un dos por ciento (de 50 a 51 empleados) aumentaría la producción en un dos por ciento y esto se llama rendimientos constantes.
Más adelante en la curva de producción, por ejemplo, con 100 empleados, es probable que el espacio en planta esté abarrotado, haya demasiada gente operando las máquinas y en el edificio, y los trabajadores se estorben entre sí. Aumentar el número de empleados en un dos por ciento (de 100 a 102 empleados) aumentaría la producción en menos del dos por ciento y a esto se le llama "rendimientos decrecientes".
Después de alcanzar el punto de máxima producción, al emplear trabajadores adicionales se obtendrán rendimientos negativos. [18]
En cada uno de estos ejemplos, la superficie útil y el capital del factor permanecieron constantes, es decir, estos insumos se mantuvieron constantes. Con solo aumentar el número de personas, la productividad y la eficiencia del proceso pasaron de rendimientos crecientes a rendimientos decrecientes.
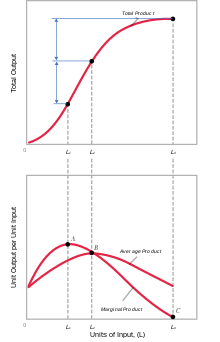
Para entender este concepto a fondo, hay que reconocer la importancia de la producción marginal o de los rendimientos marginales . Los rendimientos acaban disminuyendo porque los economistas miden la productividad en relación con las unidades adicionales (marginales). Los insumos adicionales afectan significativamente a la eficiencia o a los rendimientos en mayor medida en las etapas iniciales. [19] El punto del proceso antes de que los rendimientos empiecen a disminuir se considera el nivel óptimo. Ser capaz de reconocer este punto es beneficioso, ya que se pueden alterar otras variables de la función de producción en lugar de aumentar continuamente la mano de obra.
Además, examinemos algo como el Índice de Desarrollo Humano , que presumiblemente seguiría aumentando mientras el PIB per cápita (en términos de paridad de poder adquisitivo) estuviera aumentando. Esta sería una suposición racional porque el PIB per cápita es una función del IDH. Incluso el PIB per cápita llegará a un punto en el que tendrá una tasa de rendimiento decreciente sobre el IDH. [20] Basta pensar que, en una familia de bajos ingresos, un aumento promedio de los ingresos probablemente tendrá un gran impacto en el bienestar de la familia. Los padres podrían proporcionar una mayor cantidad de alimentos y artículos básicos de salud para su familia. Esa es una tasa de rendimiento significativamente creciente. Pero, si le diésemos el mismo aumento a una familia rica, el impacto que tendría en su vida sería menor. Por lo tanto, la tasa de rendimiento proporcionada por ese aumento promedio de los ingresos es decreciente.
Significar
Rendimientos crecientes:
Rendimientos constantes:
Rendimientos decrecientes:
Existe una función de producción ampliamente reconocida en economía: Q = f(NR, L, K, t, E) :
Partimos de la ecuación del producto marginal:
Para demostrar rendimientos decrecientes, se cumplen dos condiciones: el producto marginal es positivo y el producto marginal es decreciente.
La elasticidad , una función de la entrada y la salida, , puede tomarse para pequeños cambios de entrada. Si se cumplen las dos condiciones anteriores, entonces . [23]
Esto funciona intuitivamente;
Existe una relación inversa entre los rendimientos de los insumos y el costo de producción, [24] aunque otras características como las condiciones del mercado de insumos también pueden afectar los costos de producción. Supongamos que un kilogramo de semillas cuesta un dólar , y este precio no cambia. Supongamos para simplificar que no hay costos fijos . Un kilogramo de semillas rinde una tonelada de cosecha, por lo que la primera tonelada de cosecha cuesta un dólar para producir. Es decir, para la primera tonelada de producción, el costo marginal así como el costo promedio de la producción es por tonelada. Si no hay otros cambios, entonces si el segundo kilogramo de semillas aplicado a la tierra produce solo la mitad de la producción del primero (mostrando rendimientos decrecientes), el costo marginal sería igual a por media tonelada de producción, o por tonelada, y el costo promedio es por 3/2 toneladas de producción, o /3 por tonelada de producción. De manera similar, si el tercer kilogramo de semillas produce sólo un cuarto de tonelada, entonces el costo marginal es igual a por cuarto de tonelada o por tonelada, y el costo promedio es por 7/4 de tonelada, o 7/7 por tonelada de producción. Por lo tanto, los rendimientos marginales decrecientes implican costos marginales crecientes y costos promedio crecientes.
El costo se mide en términos de costo de oportunidad . En este caso, la ley también se aplica a las sociedades: el costo de oportunidad de producir una sola unidad de un bien generalmente aumenta a medida que una sociedad intenta producir más de ese bien. Esto explica la forma arqueada de la frontera de posibilidades de producción .
Parte de la razón por la que un insumo se altera ceteris paribus es la idea de la posibilidad de desecharlo. [25] Con este supuesto, esencialmente algunos insumos están por encima del nivel eficiente, es decir, pueden disminuir sin un impacto perceptible en la producción, de la misma manera que ocurre con el exceso de fertilizantes en un campo.
Si se supone que los insumos son desechables, entonces aumentar el insumo principal, mientras se reducen los insumos excedentes, podría resultar en el mismo "rendimiento disminuido", como si el insumo principal cambiara certeris paribus . Si bien se consideran insumos "duros", como el trabajo y los activos, los rendimientos decrecientes serían ciertos. En la era de la contabilidad moderna, donde los insumos pueden rastrearse hasta los movimientos del capital financiero, el mismo caso puede reflejar rendimientos constantes o crecientes.
Es necesario tener clara la "estructura fina" [4] de las entradas antes de continuar. En este sentido, ceteris paribus es desambiguación.