En matemáticas , el plano proyectivo real es un ejemplo de variedad bidimensional compacta no orientable ; en otras palabras, una superficie unilateral . No puede incrustarse en un espacio tridimensional estándar sin intersectarse. Tiene aplicaciones básicas a la geometría , ya que la construcción común del plano proyectivo real es como el espacio de líneas en R 3 que pasan por el origen.
El plano también se describe a menudo topológicamente, en términos de una construcción basada en la tira de Möbius : si se pudiera pegar el (único) borde de la tira de Möbius a sí mismo en la dirección correcta, se obtendría el plano proyectivo. (Esto no se puede hacer en el espacio tridimensional sin que la superficie se cruce a sí misma). De manera equivalente, pegar un disco a lo largo del límite de la tira de Möbius da el plano proyectivo. Topológicamente, tiene la característica de Euler 1, por lo tanto un semigénero (género no orientable, género Euler) de 1.
Dado que la tira de Möbius, a su vez, puede construirse a partir de un cuadrado pegando dos de sus lados con un medio giro, el plano proyectivo real puede representarse como un cuadrado unitario (es decir, [0, 1] × [ 0,1] ) con sus lados identificados por las siguientes relaciones de equivalencia :
y
como en el diagrama más a la izquierda que se muestra aquí.
La geometría proyectiva no tiene necesariamente que ver con la curvatura y el plano proyectivo real puede torcerse y colocarse en el plano euclidiano o en el espacio tridimensional de muchas maneras diferentes. [1] Algunos de los ejemplos más importantes se describen a continuación.
El plano proyectivo no puede estar incrustado (es decir, sin intersección) en el espacio euclidiano tridimensional . La prueba de que el plano proyectivo no se incrusta en el espacio euclidiano tridimensional es la siguiente: suponiendo que sí se incrusta, limitaría una región compacta en el espacio euclidiano tridimensional mediante el teorema generalizado de la curva de Jordan . El campo vectorial normal unitario que apunta hacia afuera daría entonces una orientación de la variedad límite, pero la variedad límite sería el plano proyectivo , que no es orientable. Esto es una contradicción, por lo que nuestra suposición de que sí se incrusta debe haber sido falsa.
Considere una esfera , y sean los círculos máximos de la esfera "líneas" y los pares de puntos antípodas sean "puntos". Es fácil comprobar que este sistema obedece a los axiomas exigidos a un plano proyectivo :
Si identificamos cada punto de la esfera con su punto antípoda, obtenemos una representación del plano proyectivo real en el que los "puntos" del plano proyectivo son realmente puntos. Esto significa que el plano proyectivo es el espacio cociente de la esfera obtenido al dividir la esfera en clases de equivalencia bajo la relación de equivalencia ~, donde x ~ y si y = x o y = − x . Este espacio cociente de la esfera es homeomorfo con el conjunto de todas las rectas que pasan por el origen en R 3 .
El mapa cociente de la esfera al plano proyectivo real es de hecho un mapa de cobertura de dos láminas (es decir, dos a uno) . De ello se deduce que el grupo fundamental del plano proyectivo real es el grupo cíclico de orden 2; es decir, enteros módulo 2. Se puede tomar el bucle AB de la figura anterior como generador.

Debido a que la esfera cubre dos veces el plano proyectivo real, el plano puede representarse como un hemisferio cerrado alrededor de cuyo borde se identifican puntos opuestos. [2]
El plano proyectivo puede sumergirse (las vecindades locales del espacio fuente no tienen autointersecciones) en 3 espacios. La superficie del niño es un ejemplo de inmersión.
Los ejemplos poliédricos deben tener al menos nueve caras. [3]

La superficie romana de Steiner es un mapa más degenerado del plano proyectivo en 3 espacios, que contiene una cruz .

Una representación poliédrica es el tetrahemihexaedro , [4] que tiene la misma forma general que la superficie romana de Steiner, que se muestra aquí.
Mirando en la dirección opuesta, ciertos politopos regulares abstractos ( hemicubo , hemidodecaedro y hemiicosaedro ) pueden construirse como figuras regulares en el plano proyectivo; ver también poliedros proyectivos .
Se han descrito varias proyecciones o mapeos planos (planos) del plano proyectivo. En 1874, Klein describió el mapeo: [1]
La proyección central del hemisferio proyectivo sobre un plano produce el plano proyectivo infinito habitual, que se describe a continuación.
Se obtiene una superficie cerrada pegando un disco a una tapa transversal . Esta superficie se puede representar paramétricamente mediante las siguientes ecuaciones:
donde tanto u como v oscilan entre 0 y 2 π .
Estas ecuaciones son similares a las de un toroide . La Figura 1 muestra un disco cerrado con tapa cruzada.
Un disco con tapa cruzada tiene un plano de simetría que pasa por su segmento de recta de puntos dobles. En la Figura 1, el disco con tapa cruzada se ve desde arriba de su plano de simetría z = 0, pero se vería igual si se viera desde abajo.
Un disco con tapa cruzada se puede cortar a lo largo de su plano de simetría, asegurándose de no cortar a lo largo de ninguno de sus puntos dobles. El resultado se muestra en la Figura 2.
Una vez que se hace esta excepción, se verá que el disco con tapa cruzada cortado es homeomorfo a un disco que se interseca a sí mismo, como se muestra en la Figura 3.
El disco que se interseca a sí mismo es homeomorfo a un disco ordinario. Las ecuaciones paramétricas del disco que se intersecta a sí mismo son:
donde u oscila entre 0 y 2 π y v oscila entre 0 y 1.
Al proyectar el disco que se intersecta a sí mismo sobre el plano de simetría ( z = 0 en la parametrización dada anteriormente) que pasa sólo por los puntos dobles, el resultado es un disco ordinario que se repite (se duplica sobre sí mismo).
El plano z = 0 corta el disco que se interseca en un par de discos que son reflejos especulares entre sí. Los discos tienen centros en el origen .
Consideremos ahora los bordes de los discos (con v = 1). Los puntos en el borde del disco que se corta a sí mismo vienen en pares que son reflejos entre sí con respecto al plano z = 0.
Se forma un disco con tapa cruzada identificando estos pares de puntos, haciéndolos equivalentes entre sí. Esto significa que un punto con parámetros ( u , 1) y coordenadas se identifica con el punto ( u + π, 1) cuyas coordenadas son . Pero esto significa que los pares de puntos opuestos en el borde del disco ordinario (equivalente) se identifican entre sí; Así se forma un plano proyectivo real a partir de un disco. Por lo tanto, la superficie que se muestra en la Figura 1 (tapa transversal con disco) es topológicamente equivalente al plano proyectivo real RP 2 .
Los puntos del plano se pueden representar mediante coordenadas homogéneas . Un punto tiene coordenadas homogéneas [ x : y : z ], donde se considera que las coordenadas [ x : y : z ] y [ tx : ty : tz ] representan el mismo punto, para todos los valores distintos de cero de t . Los puntos con coordenadas [ x : y :1] son el plano real habitual , llamado parte finita del plano proyectivo, y los puntos con coordenadas [ x : y :0], llamados puntos en el infinito o puntos ideales , constituyen una recta llamada la recta en el infinito . (Las coordenadas homogéneas [0: 0: 0] no representan ningún punto).
Las líneas en el plano también se pueden representar mediante coordenadas homogéneas. Una recta proyectiva correspondiente al plano ax + by + cz = 0 en R 3 tiene coordenadas homogéneas ( a : b : c ). Por lo tanto, estas coordenadas tienen la relación de equivalencia ( a : b : c ) = ( da : db : dc ) para todos los valores distintos de cero de d . Por tanto, una ecuación diferente de la misma recta dax + dby + dcz = 0 da las mismas coordenadas homogéneas. Un punto [ x : y : z ] se encuentra en una recta ( a : b : c ) si ax + by + cz = 0. Por lo tanto, rectas con coordenadas ( a : b : c ) donde a , b no son ambas 0 corresponden a las rectas en el plano real habitual , porque contienen puntos que no están en el infinito. La recta de coordenadas (0 : 0 : 1) es la recta en el infinito, ya que los únicos puntos en ella son aquellos con z = 0.
Una línea en P 2 se puede representar mediante la ecuación ax + by + cz = 0. Si tratamos a , b y c como el vector columna ℓ y x , y , z como el vector columna x , entonces la ecuación anterior puede ser escrito en forma matricial como:
Usando notación vectorial podemos escribir x ⋅ ℓ = 0 o ℓ ⋅ x = 0.
La ecuación k ( x T ℓ ) = 0 (que k es un escalar distinto de cero) barre un plano que pasa por cero en R 3 y k ( x ) barre una línea que nuevamente pasa por cero. El plano y la recta son subespacios lineales en R 3 , que siempre pasan por cero.
En P 2 la ecuación de una recta es ax + by + cz = 0 y esta ecuación puede representar una recta en cualquier plano paralelo al plano x , y multiplicando la ecuación por k .
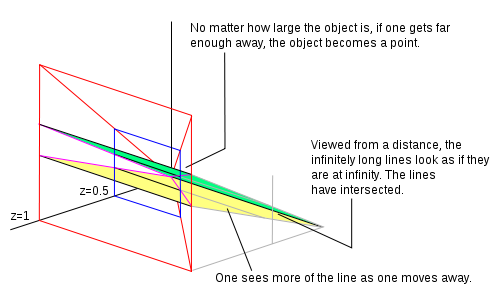
Si z = 1 tenemos una coordenada homogénea normalizada. Todos los puntos que tienen z = 1 crean un plano. Supongamos que estamos mirando ese plano (desde una posición más alejada a lo largo del eje z y mirando hacia el origen) y hay dos líneas paralelas dibujadas en el plano. Desde donde estamos (dadas nuestras capacidades visuales) solo podemos ver una parte del avión, que representamos como el área delineada en rojo en el diagrama. Si nos alejamos del avión a lo largo del eje z (aún mirando hacia atrás, hacia el origen), podemos ver más del avión. En nuestro campo de visión los puntos originales se han movido. Podemos reflejar este movimiento dividiendo la coordenada homogénea por una constante. En la imagen adyacente hemos dividido por 2, por lo que el valor z ahora pasa a ser 0,5. Si nos alejamos lo suficiente lo que estamos mirando se convierte en un punto en la distancia. A medida que nos alejamos vemos más y más líneas paralelas. Las líneas se encontrarán en una línea en el infinito (una línea que pasa por cero en el plano en z = 0 ). Las rectas en el plano cuando z = 0 son puntos ideales. El plano en z = 0 es la recta en el infinito.
El punto homogéneo (0, 0, 0) es donde van todos los puntos reales cuando miras el plano desde una distancia infinita, una línea en el plano z = 0 es donde se cruzan las líneas paralelas.
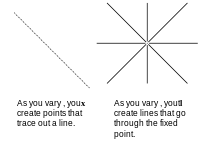
En la ecuación x T ℓ = 0 hay dos vectores columna . Puedes mantener cualquiera de ellos constante y variar el otro. Si mantenemos constante el punto x y variamos los coeficientes ℓ creamos nuevas rectas que pasan por el punto. Si mantenemos constantes los coeficientes y variamos los puntos que satisfacen la ecuación creamos una recta. Consideramos a x como un punto, porque los ejes que utilizamos son x , y y z . Si, en cambio, graficamos los coeficientes usando los ejes marcados con a , b , c , los puntos se convertirían en líneas y las líneas en puntos. Si prueba algo con los datos trazados en el eje marcado x , y , z , se puede usar el mismo argumento para los datos trazados en el eje marcado a , byc . Esa es la dualidad.
La ecuación x T ℓ = 0 calcula el producto interno de dos vectores de columna. El producto interno de dos vectores es cero si los vectores son ortogonales . En P 2 , la línea entre los puntos x 1 y x 2 se puede representar como un vector columna ℓ que satisface las ecuaciones x 1 T ℓ = 0 y x 2 T ℓ = 0 , o en otras palabras, un vector columna ℓ que es ortogonal a x 1 y x 2 . El producto vectorial encontrará dicho vector: la línea que une dos puntos tiene coordenadas homogéneas dadas por la ecuación x 1 × x 2 . La intersección de dos rectas se puede encontrar de la misma manera, usando la dualidad, como el producto cruzado de los vectores que representan las rectas, ℓ 1 × ℓ 2 .
El plano proyectivo se integra en el espacio euclidiano de 4 dimensiones. El plano proyectivo real P 2 ( R ) es el cociente de las dos esferas
por la relación antípoda ( x , y , z ) ~ (− x , − y , − z ) . Considere la función R 3 → R 4 dada por ( x , y , z ) ↦ ( xy , xz , y 2 − z 2 , 2 yz ) . Este mapa se restringe a un mapa cuyo dominio es S 2 y, dado que cada componente es un polinomio homogéneo de grado par, toma los mismos valores en R 4 en cada uno de dos puntos antípodas cualesquiera en S 2 . Esto produce un mapa P 2 ( R ) → R 4 . Además, este mapa es una incrustación. Observe que esta incrustación admite una proyección en R 3 que es la superficie romana .
Pegando sucesivamente planos proyectivos obtenemos superficies no orientables de semigénero superiores . El proceso de pegado consiste en recortar un pequeño disco de cada superficie e identificar ( pegar ) sus círculos delimitadores. Al pegar dos planos proyectivos se crea la botella de Klein .
El artículo sobre el polígono fundamental describe las superficies superiores no orientables.