
En ingeniería estructural , la deflexión es el grado en el que una parte de un elemento estructural largo (como una viga ) se deforma lateralmente (en la dirección transversal a su eje longitudinal) bajo una carga . Puede cuantificarse en términos de un ángulo ( desplazamiento angular ) o una distancia ( desplazamiento lineal ). Una deformación longitudinal (en la dirección del eje) se denomina elongación .
La distancia de deflexión de un elemento bajo una carga se puede calcular integrando la función que describe matemáticamente la pendiente de la forma desviada del elemento bajo esa carga. Existen fórmulas estándar para la deflexión de configuraciones de vigas comunes y casos de carga en ubicaciones discretas. De lo contrario, se utilizan métodos como el trabajo virtual , la integración directa , el método de Castigliano , el método de Macaulay o el método de rigidez directa . La deflexión de los elementos de viga generalmente se calcula sobre la base de la ecuación de viga de Euler-Bernoulli , mientras que la de un elemento de placa o cáscara se calcula utilizando la teoría de placas o cáscaras .
Un ejemplo del uso de la deflexión en este contexto es la construcción de edificios. Los arquitectos e ingenieros seleccionan materiales para diversas aplicaciones.
Las vigas pueden variar mucho en cuanto a su geometría y composición. Por ejemplo, una viga puede ser recta o curva. Puede tener una sección transversal constante o puede estrecharse. Puede estar hecha completamente del mismo material (homogénea) o puede estar compuesta de diferentes materiales (compuesta). Algunas de estas características dificultan el análisis, pero muchas aplicaciones de ingeniería implican casos que no son tan complicados. El análisis se simplifica si:
En este caso, la ecuación que rige la deflexión de la viga ( ) se puede aproximar como: donde la segunda derivada de su forma deflexionada con respecto a ( siendo la posición horizontal a lo largo de la longitud de la viga) se interpreta como su curvatura, es el módulo de Young , es el momento de inercia del área de la sección transversal, y es el momento de flexión interno en la viga.
Si además la viga no es cónica y es homogénea , y sobre ella actúa una carga distribuida , la expresión anterior se puede escribir como :
Esta ecuación se puede resolver para una variedad de condiciones de carga y de contorno. A continuación se muestran varios ejemplos simples. Las fórmulas expresadas son aproximaciones desarrolladas para vigas prismáticas largas, delgadas, homogéneas, con pequeñas deflexiones y propiedades elásticas lineales. Con estas restricciones, las aproximaciones deberían dar resultados dentro del 5 % de la deflexión real.
Las vigas en voladizo tienen un extremo fijo, por lo que la pendiente y la desviación en ese extremo deben ser cero.

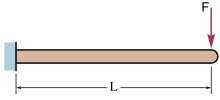
La deflexión elástica y el ángulo de deflexión (en radianes ) en el extremo libre en la imagen de ejemplo: Una viga en voladizo (sin peso) , con una carga en el extremo, se puede calcular (en el extremo libre B) usando: [1] donde
Obsérvese que si el tramo se duplica, la deflexión se multiplica por ocho. La deflexión en cualquier punto, , a lo largo del tramo de una viga voladiza cargada en un extremo se puede calcular utilizando: [1]
Nota: En (el extremo de la viga), las ecuaciones y son idénticas a las ecuaciones y anteriores.

La deflexión, en el extremo libre B, de una viga en voladizo bajo una carga uniforme viene dada por: [1] donde
La deflexión en cualquier punto, , a lo largo del tramo de una viga en voladizo cargada uniformemente se puede calcular utilizando: [1]
Las vigas simplemente apoyadas tienen soportes debajo de sus extremos que permiten la rotación, pero no la deflexión.


La deflexión en cualquier punto, , a lo largo del tramo de una viga simplemente apoyada con carga central se puede calcular utilizando: [1] para
El caso especial de deflexión elástica en el punto medio C de una viga, cargada en su centro, sostenida por dos apoyos simples viene dado por: [1] donde

La deflexión elástica máxima en una viga sostenida por dos apoyos simples, cargada a una distancia del apoyo más cercano, viene dada por: [1] donde
Esta deflexión máxima se produce a una distancia del soporte más cercano y viene dada por: [1]

La deflexión elástica (en el punto medio C) de una viga sostenida por dos soportes simples, bajo una carga uniforme (como se muestra en la imagen) viene dada por: [1] donde
La deflexión en cualquier punto, , a lo largo del tramo de una viga simplemente apoyada y cargada uniformemente se puede calcular utilizando: [1]
La deflexión de vigas con una combinación de cargas simples se puede calcular utilizando el principio de superposición .
El cambio de longitud de la viga, proyectada a lo largo de la línea de la viga sin carga, se puede calcular integrando la función de pendiente, si la función de deflexión es conocida para todos los .
Dónde:
Si la viga es uniforme y se conoce la desviación en cualquier punto, ésta se puede calcular sin conocer otras propiedades de la viga.
Las fórmulas proporcionadas anteriormente requieren el uso de un conjunto coherente de unidades. La mayoría de los cálculos se realizarán en el Sistema Internacional de Unidades (SI) o en unidades habituales de EE. UU., aunque existen muchos otros sistemas de unidades.
También se pueden utilizar otras unidades, siempre que sean coherentes entre sí. Por ejemplo, a veces se utiliza la unidad kilogramo-fuerza ( ) para medir cargas. En tal caso, el módulo de elasticidad debe convertirse a .
Los códigos de construcción determinan la deflexión máxima, generalmente como una fracción de la distancia, por ejemplo, 1/400 o 1/600. Tanto el estado límite de resistencia (tensión admisible) como el estado límite de servicio (consideraciones de deflexión, entre otras) pueden determinar las dimensiones mínimas requeridas del elemento.
La deflexión debe tenerse en cuenta para el propósito de la estructura. Al diseñar un marco de acero para sostener un panel vidriado, se permite solo una deflexión mínima para evitar la fractura del vidrio.
La forma desviada de una viga se puede representar mediante el diagrama de momentos , integrado (dos veces, rotado y trasladado para imponer las condiciones de apoyo).