problema de secretaria

Problema matemático que involucra la teoría de parada óptima.

Gráficos de probabilidades de obtener el mejor candidato (círculos rojos) de n aplicaciones, y k / n (cruces azules) donde k es el tamaño de la muestra

El problema de la secretaria demuestra un escenario que involucra la teoría de parada óptima ^{[1] [2]} que se estudia ampliamente en los campos de la probabilidad aplicada , la estadística y la teoría de la decisión . También se le conoce como el problema del matrimonio , el problema de la dote del sultán , el problema del pretendiente quisquilloso , el juego del googol y el problema de la mejor elección . Su solución también se conoce como regla del 37% . ^[3]

La forma básica del problema es la siguiente: imaginemos un administrador que quiere contratar a la mejor secretaria entre candidatos clasificados para un puesto. Los solicitantes son entrevistados uno por uno en orden aleatorio. Se debe tomar una decisión sobre cada solicitante en particular inmediatamente después de la entrevista. Una vez rechazado, un solicitante no puede ser revocado. Durante la entrevista, el administrador obtiene información suficiente para clasificar al solicitante entre todos los solicitantes entrevistados hasta el momento, pero desconoce la calidad de los solicitantes aún no vistos. La pregunta es sobre la estrategia óptima ( regla de detención ) para maximizar la probabilidad de seleccionar al mejor solicitante. Si la decisión se puede aplazar hasta el final, esto se puede resolver mediante el simple algoritmo de selección máxima de seguimiento del máximo actual (y quién lo alcanzó) y seleccionando el máximo general al final. La dificultad es que la decisión debe tomarse de inmediato. ${\displaystyle n}$

La prueba rigurosa más corta conocida hasta ahora la proporciona el algoritmo de probabilidades . Implica que la probabilidad óptima de ganar es siempre al menos (donde e es la base del logaritmo natural ), y que este último se cumple incluso en una generalidad mucho mayor. La regla de parada óptima prescribe rechazar siempre a los primeros solicitantes que sean entrevistados y luego detenerse en el primer solicitante que sea mejor que todos los solicitantes entrevistados hasta el momento (o continuar hasta el último solicitante si esto nunca ocurre). A veces, esta estrategia se denomina regla de detención, porque la probabilidad de detenerse en el mejor candidato con esta estrategia ya es aproximadamente para valores moderados de . Una de las razones por las que el problema de la secretaria ha recibido tanta atención es que la política óptima para el problema (la regla de detención) es simple y selecciona al mejor candidato alrededor del 37% de las veces, independientemente de si hay 100 o 100 millones de solicitantes. ${\displaystyle 1/e}$ ${\displaystyle \sim n/e}$ ${\displaystyle 1/e}$ ${\displaystyle 1/e}$ ${\displaystyle n}$

Formulación

Aunque existen muchas variaciones, el problema básico se puede plantear de la siguiente manera:

• Hay un único puesto a cubrir.
• Hay n solicitantes para el puesto y se conoce el valor de n .
• Los solicitantes, si se ven todos juntos, se pueden clasificar de mejor a peor sin ambigüedades.
• Los solicitantes son entrevistados secuencialmente en orden aleatorio, siendo cada orden igualmente probable.
• Inmediatamente después de una entrevista, el solicitante entrevistado es aceptado o rechazado y la decisión es irrevocable.
• La decisión de aceptar o rechazar a un solicitante puede basarse únicamente en los rangos relativos de los solicitantes entrevistados hasta el momento.
• El objetivo de la solución general es tener la mayor probabilidad de seleccionar al mejor candidato de todo el grupo. Esto es lo mismo que maximizar la recompensa esperada, definiéndose la recompensa como uno para el mejor solicitante y cero en caso contrario.

Un candidato se define como un solicitante que, cuando es entrevistado, es mejor que todos los solicitantes entrevistados anteriormente. Saltar se utiliza para significar "rechazar inmediatamente después de la entrevista". Dado que el objetivo del problema es seleccionar al mejor solicitante, solo se considerarán los candidatos para su aceptación. El "candidato" en este contexto corresponde al concepto de registro en permutación.

Derivando la política óptima

La política óptima para el problema es una regla de detención . Según él, el entrevistador rechaza a los primeros r  − 1 solicitantes (deje que el solicitante M sea el mejor solicitante entre estos r  − 1 solicitantes) y luego selecciona al primer solicitante posterior que sea mejor que el solicitante M. Se puede demostrar que la estrategia óptima se encuentra en esta clase de estrategias. ^{[ cita necesaria ]} (Tenga en cuenta que nunca debemos elegir un solicitante que no sea el mejor que hemos visto hasta ahora, ya que no puede ser el mejor solicitante en general). Para un límite arbitrario r , la probabilidad de que se seleccione al mejor solicitante es

${\displaystyle {\begin{aligned}P(r)&=\sum _{i=1}^{n}P\left({\text{applicant }}i{\text{ is selected}}\cap {\text{applicant }}i{\text{ is the best}}\right)\\&=\sum _{i=1}^{n}P\left({\text{applicant }}i{\text{ is selected}}|{\text{applicant }}i{\text{ is the best}}\right)\cdot P\left({\text{applicant }}i{\text{ is the best}}\right)\\&=\left[\sum _{i=1}^{r-1}0+\sum _{i=r}^{n}P\left(\left.{\begin{array}{l}{\text{the best of the first }}i-1{\text{ applicants}}\\{\text{is in the first }}r-1{\text{ applicants}}\end{array}}\right|{\text{applicant }}i{\text{ is the best}}\right)\right]\cdot {\frac {1}{n}}\\&=\left[\sum _{i=r}^{n}{\frac {r-1}{i-1}}\right]\cdot {\frac {1}{n}}\\&={\frac {r-1}{n}}\sum _{i=r}^{n}{\frac {1}{i-1}}.\end{aligned}}}$

La suma no está definida para r = 1, pero en este caso la única política factible es seleccionar al primer solicitante y, por tanto, P (1) = 1/ n . Esta suma se obtiene observando que si el solicitante i es el mejor solicitante, entonces se selecciona si y sólo si el mejor solicitante entre los primeros i  − 1 solicitantes está entre los primeros r  − 1 solicitantes que fueron rechazados. Dejando que n tienda al infinito, escribiendo como el límite de (r−1) / n , usando t para (i−1) / n y dt para 1/ n , la suma se puede aproximar mediante la integral ${\displaystyle x}$

${\displaystyle P(x)=x\int _{x}^{1}{\frac {1}{t}}\,dt=-x\ln(x)\;.}$

Tomando la derivada de P ( x ) con respecto a , estableciéndola en 0 y resolviendo x , encontramos que la x óptima es igual a 1/ e . Por lo tanto, el límite óptimo tiende a n / e a medida que n aumenta, y el mejor solicitante se selecciona con probabilidad 1/ e . ${\displaystyle x}$

Para valores pequeños de n , la r óptima también se puede obtener mediante métodos de programación dinámica estándar . Los umbrales óptimos r y la probabilidad de seleccionar la mejor alternativa P para varios valores de n se muestran en la siguiente tabla. ^{[nota 1]}

La probabilidad de seleccionar al mejor candidato en el problema clásico de la secretaria converge hacia . ${\displaystyle 1/e\approx 0.368}$

Solución alternativa

Este problema y varias modificaciones pueden resolverse (incluida la prueba de optimidad) de manera sencilla mediante el algoritmo de probabilidades , que también tiene otras aplicaciones. Las modificaciones del problema de la secretaria que pueden resolverse con este algoritmo incluyen disponibilidades aleatorias de los solicitantes, hipótesis más generales para que los solicitantes sean de interés para quien toma las decisiones, entrevistas grupales para los solicitantes, así como ciertos modelos para un número aleatorio de solicitantes. ^{[ cita necesaria ]}

Limitaciones

La solución del problema de la secretaria sólo tiene sentido si está justificado suponer que los solicitantes no tienen conocimiento de la estrategia de decisión empleada, porque los primeros solicitantes no tienen ninguna posibilidad y, de lo contrario, es posible que no se presenten.

Un inconveniente importante para las aplicaciones de la solución del problema clásico de la secretaria es que se debe conocer de antemano el número de solicitantes, lo que rara vez ocurre. Una forma de superar este problema es suponer que el número de solicitantes es una variable aleatoria con una distribución conocida (Presman y Sonin, 1972). Sin embargo, para este modelo, la solución óptima es en general mucho más difícil. Además, la probabilidad óptima de éxito ya no es de alrededor de 1/ e , sino que suele ser inferior. Esto puede entenderse en el contexto de tener un "precio" que pagar por no saber el número de solicitantes. Sin embargo, en este modelo el precio es elevado. Dependiendo de la elección de la distribución de , la probabilidad óptima de ganar puede acercarse a cero. La búsqueda de formas de afrontar este nuevo problema condujo a un nuevo modelo que produjo la llamada ley 1/e de la mejor elección. ${\displaystyle n}$ ${\displaystyle N}$ ${\displaystyle P(N=k)_{k=1,2,\cdots }}$ ${\displaystyle N}$

1/e-ley de mejor elección

La esencia del modelo se basa en la idea de que la vida es secuencial y que los problemas del mundo real se plantean en tiempo real. Además, es más fácil estimar los tiempos en que eventos específicos (llegadas de solicitantes) deberían ocurrir con mayor frecuencia (si es que ocurren) que estimar la distribución del número de eventos específicos que ocurrirán. Esta idea condujo al siguiente enfoque, el llamado enfoque unificado (1984):

El modelo se define de la siguiente manera: un solicitante debe ser seleccionado en algún intervalo de tiempo entre un número desconocido de solicitantes clasificables. El objetivo es maximizar la probabilidad de seleccionar sólo los mejores bajo la hipótesis de que todos los pedidos de llegada de diferentes rangos son igualmente probables. Supongamos que todos los solicitantes tienen la misma, pero independientes entre sí, densidad de tiempo de llegada y denotamos la función de distribución de tiempo de llegada correspondiente, es decir ${\displaystyle [0,T]}$ ${\displaystyle N}$ ${\displaystyle f}$ ${\displaystyle [0,T]}$ ${\displaystyle F}$

${\displaystyle F(t)=\int _{0}^{t}f(s)ds}$, . ${\displaystyle \,0\leq t\leq T}$

Sea tal que considere la estrategia de esperar y observar a todos los solicitantes hasta el momento y luego seleccionar, si es posible, el primer candidato después del tiempo que sea mejor que todos los anteriores. Entonces esta estrategia, llamada estrategia 1/e , tiene las siguientes propiedades: ${\displaystyle \tau }$ ${\displaystyle F(\tau )=1/e.}$ ${\displaystyle \tau }$ ${\displaystyle \tau }$

La estrategia 1/e

(i) produce para todos una probabilidad de éxito de al menos 1/e, ${\displaystyle N}$

(ii) es una estrategia minimax óptima para el selector que no sabe , ${\displaystyle N}$

(iii) selecciona, si hay al menos un solicitante, ninguno con una probabilidad exactamente 1/e.

La ley 1/e, demostrada en 1984 por F. Thomas Bruss , fue una sorpresa. La razón fue que antes se consideraba que un valor de aproximadamente 1/e estaba fuera de alcance en un modelo para desconocido , mientras que este valor 1/e ahora se alcanzaba como límite inferior para la probabilidad de éxito, y esto en un modelo con posiblemente hipótesis mucho más débiles (ver, por ejemplo, Math. Reviews 85:m). ${\displaystyle N}$

Sin embargo, hay muchas otras estrategias que logran (i) y (ii) y, además, funcionan estrictamente mejor que la estrategia 1/e simultáneamente para todos >2. Un ejemplo simple es la estrategia que selecciona (si es posible) al primer candidato relativamente mejor después de un tiempo, siempre que al menos un solicitante haya llegado antes de este tiempo, y en caso contrario selecciona (si es posible) al segundo candidato relativamente mejor después de un tiempo . ^[4] ${\displaystyle N}$ ${\displaystyle \tau }$ ${\displaystyle \tau }$

La ley 1/e a veces se confunde con la solución al problema clásico de la secretaria descrito anteriormente debido al papel similar del número 1/e. Sin embargo, en la Ley 1/e, este papel es más general. El resultado también es más sólido, ya que es válido para un número desconocido de solicitantes y dado que el modelo basado en una distribución del tiempo de llegada F es más manejable para las solicitudes.

El juego del googol.

En el artículo "¿Quién resolvió el problema del Secretario?" ( Ferguson , 1989) ^[1] , se afirma que el problema de la secretaria apareció impreso por primera vez en la columna Mathematical Games de febrero de 1960 de Martin Gardner en Scientific American :

Pídale a alguien que tome tantas hojas de papel como quiera y en cada hoja escriba un número positivo diferente. Los números pueden variar desde pequeñas fracciones de 1 hasta un número del tamaño de un googol (1 seguido de cien ceros) o incluso mayores. Estas hojas se ponen boca abajo y se barajan sobre la parte superior de una mesa. Uno a la vez, pones las tiras boca arriba. El objetivo es dejar de girar cuando llegues al número que supones que es el mayor de la serie. No puedes regresar y recoger un papelito previamente entregado. Si entregas todas las tiras, entonces, por supuesto, debes elegir la última que se volteó. ^[5]

Ferguson señaló que el juego de la secretaria seguía sin resolverse, ya que era un juego de suma cero con dos jugadores antagónicos. ^[1] En este juego:

• Alice, la jugadora informada, escribe en secreto números distintos en las tarjetas. ${\displaystyle n}$
• Bob, el jugador que detiene, observa los valores reales y puede dejar de girar las cartas cuando quiera, ganando si la última carta volteada tiene el número máximo total.
• Bob quiere adivinar el número máximo con la probabilidad más alta posible, mientras que el objetivo de Alice es mantener esta probabilidad lo más baja posible.

La diferencia con el problema básico de la secretaria son dos:

• Alice no tiene que escribir números uniformemente al azar. Puede escribirlos según cualquier distribución de probabilidad conjunta para engañar a Bob.
• Bob observa los valores reales escritos en las tarjetas, que puede utilizar en sus procedimientos de decisión.

Análisis estratégico

Alice primero escribe n números, que luego se mezclan. Entonces, su orden no importa, lo que significa que los números de Alice deben ser una secuencia de variables aleatorias intercambiables . La estrategia de Alice es entonces simplemente elegir la secuencia de variables aleatorias intercambiables más complicada. ${\displaystyle X_{1},X_{2},...,X_{n}}$

La estrategia de Bob se puede formalizar como una regla de detención de la secuencia . ${\displaystyle \tau }$ ${\displaystyle X_{1},X_{2},...,X_{n}}$

Decimos que una regla de detención para Bob es una estrategia de detención de rango relativo si depende sólo de los rangos relativos de y no de sus valores numéricos. En otras palabras, es como si alguien interviniera en secreto después de que Alice escogiera sus números y cambiara cada número a su rango relativo (rompiendo empates al azar). Por ejemplo, se cambia a o con igual probabilidad. Esto hace que sea como si Alice jugara una permutación aleatoria intercambiable . Ahora, dado que la única permutación aleatoria intercambiable en es simplemente la distribución uniforme sobre todas las permutaciones en , la estrategia de parada de rango relativo óptima es la regla de parada óptima para el problema de la secretaria, dada anteriormente, con una probabilidad de ganar. El objetivo de Alice entonces es asegurarse de que Bob No hay nada mejor que la estrategia de parada de rango relativo. ${\displaystyle \tau }$ ${\displaystyle X_{1},X_{2},...,X_{n}}$ ${\displaystyle X_{1},X_{2},...,X_{n}}$ ${\displaystyle 0.2,0.3,0.3,0.1}$ ${\displaystyle 2,3,4,1}$ ${\displaystyle 2,4,3,1}$ ${\displaystyle \{1,2,...,n\}}$ ${\displaystyle \{1,2,...,n\}}$ ${\displaystyle \{1,2,...,n\}}$ $${\displaystyle Pr(X_{\tau }=\max _{i\in 1:n}X_{i})=\max _{r\in 1:n}{\frac {r-1}{n}}\sum _{i=r}^{n}{\frac {1}{i-1}}}$$

Según las reglas del juego, la secuencia de Alice debe ser intercambiable, pero para tener un buen desempeño en el juego, Alice no debe elegirla para que sea independiente. Si Alice toma muestras de los números independientemente de alguna distribución fija, le permitiría a Bob hacerlo mejor. Para ver esto intuitivamente, imagina si , y Alice debe elegir ambos números de la distribución normal , de forma independiente. Entonces, si Bob voltea un número y ve , entonces puede voltear con bastante confianza el segundo número, y si Bob voltea un número y ve , entonces puede escoger con bastante confianza el primer número. Alice puede hacerlo mejor seleccionando aquellas que estén correlacionadas positivamente. ${\displaystyle n=2}$ ${\displaystyle N(0,1)}$ ${\displaystyle -3}$ ${\displaystyle +3}$ ${\displaystyle X_{1},X_{2}}$

Entonces la declaración completamente formal es la siguiente:

¿Existe una secuencia intercambiable de variables aleatorias , tal que para cualquier regla de detención , ? ${\displaystyle X_{1},...,X_{n}}$ ${\displaystyle \tau }$ $${\displaystyle Pr(X_{\tau }=\max _{i\in 1:n}X_{i})\leq \max _{r\in 1:n}{\frac {r-1}{n}}\sum _{i=r}^{n}{\frac {1}{i-1}}}$$

Solución

Por ejemplo , si Bob juega la estrategia óptima de parada de rango relativo, entonces Bob tiene una probabilidad de ganar de 1/2. Sorprendentemente, Alice no tiene una estrategia minimax , lo que está estrechamente relacionado con la paradoja de T. Cover ^[6] y la paradoja de las dos envolturas . Concretamente, Bob puede jugar esta estrategia: muestrear un número aleatorio . Si , entonces elige , si no, elige . Ahora, Bob puede ganar con una probabilidad estrictamente mayor que 1/2. Supongamos que los números de Alice son diferentes, entonces condicional a que Bob gane con probabilidad 1/2, pero condicional a que Bob gane con probabilidad 1. ${\displaystyle n=2}$ ${\displaystyle Y}$ ${\displaystyle X_{1}>Y}$ ${\displaystyle X_{1}}$ ${\displaystyle X_{2}}$ ${\displaystyle Y\not \in [\min(X_{1},X_{2}),\max(X_{1},X_{2})]}$ ${\displaystyle Y\in [\min(X_{1},X_{2}),\max(X_{1},X_{2})]}$

Tenga en cuenta que el número aleatorio se puede muestrear a partir de cualquier distribución aleatoria, siempre que tenga una probabilidad distinta de cero. ${\displaystyle Y}$ ${\displaystyle Y\in [\min(X_{1},X_{2}),\max(X_{1},X_{2})]}$

Sin embargo, para cualquier , Alice puede construir una secuencia intercambiable tal que la probabilidad de ganar de Bob sea como máximo . ^[1] ${\displaystyle \epsilon >0}$ ${\displaystyle X_{1},X_{2}}$ ${\displaystyle 1/2+\epsilon }$

Pero para , la respuesta es sí: Alice puede elegir números aleatorios (que son variables aleatorias dependientes) de tal manera que Bob no puede jugar mejor que usando la estrategia clásica de parada basada en los rangos relativos. ^[7] ${\displaystyle n>2}$

Rendimiento heurístico

El resto del artículo trata nuevamente del problema de la secretaria para un número conocido de solicitantes.

Probabilidades de éxito esperadas para tres heurísticas

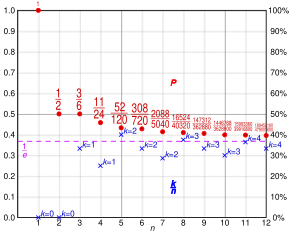
Stein, Seale y Rapoport (2003) derivaron las probabilidades de éxito esperadas para varias heurísticas psicológicamente plausibles que podrían emplearse en el problema de la secretaria. Las heurísticas que examinaron fueron:

• La regla de corte (CR): No acepte a ninguno de los primeros y solicitantes; a partir de entonces, seleccione el primer candidato encontrado (es decir, un solicitante con rango relativo 1). Esta regla tiene como caso especial la política óptima para el problema clásico de la secretaria para el cual y  =  r .
• Regla de recuento de candidatos (CCR): seleccione el yésimo candidato encontrado. Tenga en cuenta que esta regla no necesariamente omite a ningún solicitante; sólo considera cuántos candidatos han sido observados, no qué tan profundo está quien toma las decisiones en la secuencia de candidatos.
• Regla sucesiva de no candidatos (SNCR): seleccione el primer candidato encontrado después de observar y no candidatos (es decir, solicitantes con rango relativo > 1).

Cada heurística tiene un único parámetro y . La figura (que se muestra a la derecha) muestra las probabilidades de éxito esperadas para cada heurística como una función de y para problemas con n  = 80.

Variante de pago cardinal

Encontrar al mejor candidato puede parecer un objetivo bastante estricto. Se puede imaginar que el entrevistador preferiría contratar a un solicitante de mayor valor que a uno de menor valor, y no preocuparse sólo por conseguir lo mejor. Es decir, el entrevistador obtendrá algún valor al seleccionar un solicitante que no es necesariamente el mejor, y el valor derivado aumenta con el valor del candidato seleccionado.

Para modelar este problema, supongamos que los solicitantes tienen valores "verdaderos" que son variables aleatorias X extraídas de una distribución uniforme en [0, 1]. De manera similar al problema clásico descrito anteriormente, el entrevistador solo observa si cada solicitante es el mejor hasta el momento (un candidato), debe aceptar o rechazar a cada uno en el momento y debe aceptar al último si lo alcanzan. (Para ser claros, el entrevistador no conoce el rango relativo real de cada solicitante. Sólo aprende si el solicitante tiene el rango relativo 1). Sin embargo, en esta versión la recompensa viene dada por el valor real del solicitante seleccionado. Por ejemplo, si selecciona un solicitante cuyo valor real es 0,8, ganará 0,8. El objetivo del entrevistador es maximizar el valor esperado del solicitante seleccionado. ${\displaystyle n}$

Dado que los valores del solicitante iid se obtienen de una distribución uniforme en [0, 1], el valor esperado del t ésimo solicitante dado que está dado por ${\displaystyle x_{t}=\max \left\{x_{1},x_{2},\ldots ,x_{t}\right\}}$

${\displaystyle E_{t}=E\left(X_{t}|I_{t}=1\right)={\frac {t}{t+1}}.}$

Como en el problema clásico, la política óptima viene dada por un umbral, que para este problema denotaremos por , en el cual el entrevistador debería comenzar a aceptar candidatos. Bearden demostró que c es o . ^[8] (De hecho, lo que sea más cercano a .) Esto se desprende del hecho de que, dado un problema con los solicitantes, la recompensa esperada para algún umbral arbitrario es ${\displaystyle c}$ ${\displaystyle \lfloor {\sqrt {n}}\rfloor }$ ${\displaystyle \lceil {\sqrt {n}}\rceil }$ ${\displaystyle {\sqrt {n}}}$ ${\displaystyle n}$ ${\displaystyle 1\leq c\leq n}$

${\displaystyle V_{n}(c)=\sum _{t=c}^{n-1}\left[\prod _{s=c}^{t-1}\left({\frac {s-1}{s}}\right)\right]\left({\frac {1}{t+1}}\right)+\left[\prod _{s=c}^{n-1}\left({\frac {s-1}{s}}\right)\right]{\frac {1}{2}}={\frac {2cn-{c}^{2}+c-n}{2cn}}.}$

Derivando con respecto a c , se obtiene ${\displaystyle V_{n}(c)}$

${\displaystyle {\frac {\partial V}{\partial c}}={\frac {-{c}^{\,2}+n}{2{c}^{\,2}n}}.}$

Aprendizaje en el paradigma de búsqueda secuencial de información parcial. Los números muestran los valores esperados de los solicitantes según su clasificación relativa (de un total de m solicitantes vistos hasta ahora) en varios puntos de la búsqueda. Las expectativas se calculan en función del caso en que sus valores se distribuyen uniformemente entre 0 y 1. La información de rango relativo permite al entrevistador evaluar con mayor precisión a los solicitantes a medida que acumulan más puntos de datos con los que compararlos.

Dado que para todos los valores permitidos de , encontramos que se maximiza en . Dado que V es convexo en , el umbral óptimo con valores enteros debe ser o . Por lo tanto, para la mayoría de los valores, el entrevistador comenzará a aceptar solicitantes antes en la versión de pago cardinal que en la versión clásica, donde el objetivo es seleccionar al mejor solicitante. Tenga en cuenta que este no es un resultado asintótico: es válido para todos . Sin embargo, esta no es la política óptima para maximizar el valor esperado de una distribución conocida. En el caso de una distribución conocida, el juego óptimo se puede calcular mediante programación dinámica. ${\displaystyle \partial ^{\,2}V/\partial c^{\,2}<0}$ ${\displaystyle c}$ ${\displaystyle V}$ ${\displaystyle c={\sqrt {n}}}$ ${\displaystyle c}$ ${\displaystyle \lfloor {\sqrt {n}}\rfloor }$ ${\displaystyle \lceil {\sqrt {n}}\rceil }$ ${\displaystyle n}$ ${\displaystyle n}$

Una forma más general de este problema introducida por Palley y Kremer (2014) ^[9] supone que a medida que llega cada nuevo solicitante, el entrevistador observa su clasificación en relación con todos los solicitantes que han sido observados anteriormente. Este modelo es consistente con la noción de que un entrevistador aprende a medida que continúa el proceso de búsqueda acumulando un conjunto de puntos de datos pasados ​​que puede utilizar para evaluar nuevos candidatos a medida que llegan. Un beneficio de este llamado modelo de información parcial es que las decisiones y los resultados obtenidos dada la información de rango relativo se pueden comparar directamente con las decisiones y resultados óptimos correspondientes si al entrevistador se le hubiera dado información completa sobre el valor de cada solicitante. Este problema de información completa, en el que los solicitantes se seleccionan independientemente de una distribución conocida y el entrevistador busca maximizar el valor esperado del solicitante seleccionado, fue resuelto originalmente por Moser (1956), ^[10] Sakaguchi (1961), ^[11] y Karlin (1962).

Otras modificaciones

Existen varias variantes del problema de la secretaria que también tienen soluciones sencillas y elegantes.

Elija el segundo mejor, usando un intento

Una variante reemplaza el deseo de elegir lo mejor por el deseo de elegir lo segundo mejor. ^{[12] [13] [14]} Robert J. Vanderbei llama a esto el problema del "postdoctorado", argumentando que los "mejores" irán a Harvard. Para este problema, la probabilidad de éxito para un número par de solicitantes es exactamente . Esta probabilidad tiende a 1/4 cuando n tiende a infinito, lo que ilustra el hecho de que es más fácil elegir el mejor que el segundo mejor. ${\displaystyle {\frac {0.25n^{2}}{n(n-1)}}}$

Elija los k mejores, usando k intentos

Considere el problema de elegir las k mejores secretarias entre n candidatos, utilizando k intentos.

En general, el método de decisión óptimo comienza observando a los candidatos sin elegir a ninguno de ellos, luego elige a todos los candidatos que sean mejores que los primeros candidatos hasta que nos quedemos sin candidatos o selecciones. Si se mantiene constante mientras , entonces la probabilidad de éxito converge a . ^[15] Según Vanderbei 1980, si , entonces la probabilidad de éxito es . ${\displaystyle r=\left\lfloor {\frac {n}{ke^{1/k}}}\right\rfloor }$ ${\displaystyle r}$ ${\displaystyle k}$ ${\displaystyle n\to \infty }$ ${\displaystyle {\frac {1}{ek}}}$ ${\displaystyle k=n/2}$ ${\displaystyle {\frac {1}{n/2+1}}}$

Elija el mejor, utilizando múltiples intentos

En esta variante, al jugador se le permiten opciones y gana si alguna de las opciones es la mejor. Una estrategia óptima para este problema pertenece a la clase de estrategias definidas por un conjunto de números umbral , donde . ${\displaystyle r}$ ${\displaystyle (a_{1},a_{2},...,a_{r})}$ ${\displaystyle a_{1}>a_{2}>\cdots >a_{r}}$

Específicamente, imagine que tiene cartas de aceptación etiquetadas desde hasta . Tendría oficiales de solicitud, cada uno con una letra. Continúa entrevistando a los candidatos y clasificándolos en un cuadro que todos los funcionarios de solicitudes pueden ver. Ahora el oficial enviaría su carta de aceptación al primer candidato que sea mejor que todos los candidatos . (Las cartas de aceptación no enviadas se entregan por defecto a los últimos solicitantes, al igual que en el problema estándar de secretaria) ^. ${\displaystyle r}$ ${\displaystyle 1}$ ${\displaystyle r}$ ${\displaystyle r}$ ${\displaystyle i}$ ${\displaystyle 1}$ ${\displaystyle a_{i}}$

En el límite, cada uno , para algún número racional . ^[17] ${\displaystyle n\rightarrow \infty }$ ${\displaystyle a_{i}\sim ne^{-k_{i}}}$ ${\displaystyle k_{i}}$

Probabilidad de ganar

Cuando , la probabilidad de ganar converge a . De manera más general, para números enteros positivos , la probabilidad de ganar converge a , donde . ^[17] ${\displaystyle r=2}$ ${\displaystyle e^{-1}+e^{-{\frac {3}{2}}},(n\rightarrow \infty )}$ ${\displaystyle r}$ ${\displaystyle p_{1}+p_{2}+\cdots +p_{r}}$ ${\displaystyle p_{i}=\lim _{n\rightarrow \infty }{\frac {a_{i}}{n}}}$

^[16] calculado hasta , con . ${\displaystyle r=4}$ ${\displaystyle e^{-1}+e^{-{\frac {3}{2}}}+e^{-{\frac {47}{24}}}+e^{-{\frac {2761}{1152}}}}$

Matsui & Ano 2016 dieron un algoritmo general. Por ejemplo, . ${\displaystyle p_{5}=e^{-{\frac {4162637}{1474560}}}}$

Estudios experimentales

Los psicólogos y economistas experimentales han estudiado el comportamiento de decisión de personas reales en situaciones problemáticas de secretaria. ^[18] En gran parte, este trabajo ha demostrado que las personas tienden a dejar de buscar demasiado pronto. Esto puede explicarse, al menos en parte, por el costo de evaluar a los candidatos. En entornos del mundo real, esto podría sugerir que las personas no buscan lo suficiente cuando se enfrentan a problemas en los que las alternativas de decisión se encuentran secuencialmente. Por ejemplo, al intentar decidir en qué gasolinera de una carretera detenerse para repostar, es posible que las personas no busquen lo suficiente antes de detenerse. De ser cierto, entonces tenderían a pagar más por la gasolina que si hubieran buscado por más tiempo. Lo mismo puede ocurrir cuando la gente busca billetes de avión en línea. La investigación experimental sobre problemas como el problema de la secretaria a veces se denomina investigación de operaciones conductuales .

Correlatos neuronales

Si bien existe un cuerpo sustancial de investigación en neurociencia sobre la integración de información, o la representación de creencias, en tareas de toma de decisiones perceptuales que utilizan sujetos animales ^{[19] [20]} y humanos, ^[21] se sabe relativamente poco sobre cómo se toma la decisión. se llega a dejar de recopilar información.

Los investigadores han estudiado las bases neuronales para resolver el problema de la secretaria en voluntarios sanos mediante resonancia magnética funcional . ^[22] Se utilizó un proceso de decisión de Markov (MDP) para cuantificar el valor de continuar buscando versus comprometerse con la opción actual. Las decisiones de tomar o rechazar una opción involucraron las cortezas prefrontales parietales y dorsolaterales , así como el cuerpo estriado ventral , la ínsula anterior y el cingulado anterior . Por lo tanto, las regiones del cerebro previamente implicadas en la integración de evidencia y la representación de recompensas codifican cruces de umbrales que desencadenan decisiones para comprometerse con una elección.

Historia

El problema de la secretaria fue aparentemente introducido en 1949 por Merrill M. Flood , quien lo llamó el problema de la prometida en una conferencia que dio ese año. Se refirió a él varias veces durante la década de 1950, por ejemplo, en una conferencia en Purdue el 9 de mayo de 1958, y finalmente se hizo ampliamente conocido en el folklore, aunque no se publicó nada en ese momento. En 1958 envió una carta a Leonard Gillman , con copias a una docena de amigos, entre ellos Samuel Karlin y J. Robbins, esbozando una prueba de la estrategia óptima, con un apéndice de R. Palermo que demostró que todas las estrategias están dominadas por una estrategia de la forma "rechazar incondicionalmente la primera p , luego aceptar al siguiente candidato que sea mejor". ^[23]

Al parecer, la primera publicación fue de Martin Gardner en Scientific American, febrero de 1960. Se había enterado de ello por John H. Fox Jr. y L. Gerald Marnie, quienes de forma independiente habían ideado un problema equivalente en 1958; Lo llamaron el "juego de googol". Fox y Marnie no conocían la solución óptima; Gardner pidió consejo a Leo Moser , quien (junto con J.R. Pounder) proporcionó un análisis correcto para su publicación en la revista. Poco después, varios matemáticos escribieron a Gardner para contarle sobre el problema equivalente que habían escuchado a través de los rumores, todo lo cual probablemente se remonta al trabajo original de Flood. ^[24]

La ley 1/ e de mejor elección se debe a F. Thomas Bruss . ^[25]

Ferguson tiene una extensa bibliografía y señala que un problema similar (pero diferente) había sido considerado por Arthur Cayley en 1875 e incluso por Johannes Kepler mucho antes, quien pasó dos años investigando a 11 candidatos al matrimonio durante 1611-1613 después de la muerte. de su primera esposa. ^[26]

Generalización combinatoria

El problema de la secretaria se puede generalizar al caso en que hay varios trabajos diferentes. Nuevamente, los solicitantes llegan en orden aleatorio. Cuando llega un candidato, revela un conjunto de números no negativos. Cada valor especifica su calificación para uno de los trabajos. El administrador no sólo tiene que decidir si acepta o no a la solicitante sino que, en caso afirmativo, también tiene que asignarla permanentemente a uno de los puestos de trabajo. El objetivo es encontrar una tarea donde la suma de calificaciones sea la mayor posible. Este problema es idéntico a encontrar una coincidencia de peso máximo en un gráfico bipartito ponderado por bordes donde los nodos de un lado llegan en línea en orden aleatorio. Por tanto, se trata de un caso especial del problema de emparejamiento bipartito en línea . ${\displaystyle n}$ ${\displaystyle n}$

Mediante una generalización del algoritmo clásico para el problema de la secretaria, es posible obtener una asignación en la que la suma esperada de calificaciones sea sólo un factor menor que una asignación óptima (fuera de línea). ^[27] ${\displaystyle e}$

Ver también

• Portal de economía
• Portal de matemáticas

• problema de asignacion
• Algoritmo de probabilidades
• Parada óptima
• El problema de Robbins
• Teoría de la búsqueda
• Problema de matrimonio estable

Notas

1. Ferguson, Thomas S. (agosto de 1989). "¿Quién resolvió el problema de la secretaria?". Ciencia estadística . 4 (3): 282–289. doi : 10.1214/ss/1177012493 .
2. Colina, Theodore P. (2009). "Saber cuándo parar". Científico americano . 97 (2): 126-133. doi :10.1511/2009.77.126. ISSN  1545-2786. S2CID  124798270.Para la traducción al francés, consulte el artículo de portada de la edición de julio de Pour la Science (2009).
3. Thomson, Jonny (21 de abril de 2022). "Los matemáticos sugieren la" regla del 37% "para las decisiones más importantes de la vida". Gran pensamiento . Consultado el 6 de febrero de 2024 .
4. Gnedin 2021.
5. Gardner 1966.
6. Portada, Thomas M. (1987), Portada, Thomas M.; Gopinath, B. (eds.), "Elija el número más grande", Problemas abiertos en comunicación y computación , Nueva York, NY: Springer, p. 152, doi :10.1007/978-1-4612-4808-8_43, ISBN 978-1-4612-4808-8, consultado el 25 de junio de 2023
7. Gnedin 1994.
8. Barba 2006.
9. Palley, Asa B.; Kremer, Mirko (8 de julio de 2014). "Búsqueda secuencial y aprendizaje a partir de comentarios de rango: teoría y evidencia experimental". Ciencias de la gestión . 60 (10): 2525–2542. doi :10.1287/mnsc.2014.1902. ISSN  0025-1909.
10. Moser, Leo (1956). "Sobre un problema de Cayley". Scripta Matemáticas . 22 : 289–292.
11. Sakaguchi, Minoru (1 de junio de 1961). "Programación dinámica de algún diseño muestral secuencial". Revista de Análisis y Aplicaciones Matemáticas . 2 (3): 446–466. doi : 10.1016/0022-247X(61)90023-3 . ISSN  0022-247X.
12. Rosa, John S. (1982). "Selección de candidatos no extremos a partir de una secuencia aleatoria". J. Optim. Aplicación de la teoría . 38 (2): 207–219. doi :10.1007/BF00934083. ISSN  0022-3239. S2CID  121339045.
13. Szajowski, Krzysztof (1982). "Elección óptima de un objeto con rango ath". Matematyka Stosowana . Annales Societatis Mathematicae Polonae, Serie III. 10 (19): 51–65. doi : 10.14708/ma.v10i19.1533. ISSN  0137-2890.
14. Vanderbei, Robert J. (21 de junio de 2021). "La variante postdoctoral del problema de la secretaria". Aplicaciones de Mathematica . Annales Societatis Mathematicae Polonae, Serie III. 49 (1): 3–13. doi : 10.14708/ma.v49i1.7076. ISSN  2299-4009.{{cite journal}}: CS1 maint: date and year (link)
15. Girdhar y Dudek 2009.
16. Gilbert y Mosteller 1966.
17. Matsui y Ano 2016.
18. Bearden, Murphy y Rapoport, 2006; Bearden, Rapoport y Murphy, 2006; Seale y Rapoport, 1997; Palley y Kremer, 2014
19. Shadlen, MN; Newsome, WT (23 de enero de 1996). "Percepción del movimiento: ver y decidir". Procedimientos de la Academia Nacional de Ciencias . 93 (2): 628–633. Código bibliográfico : 1996PNAS...93..628S. doi : 10.1073/pnas.93.2.628 . PMC 40102 . PMID  8570606. 
20. Roitman, Jamie D.; Shadlen, Michael N. (1 de noviembre de 2002). "Respuesta de las neuronas en el área intraparietal lateral durante una tarea combinada de tiempo de reacción de discriminación visual". La Revista de Neurociencia . 22 (21): 9475–9489. doi :10.1523/JNEUROSCI.22-21-09475.2002. PMC 6758024 . PMID  12417672. 
21. Heekeren, Hauke ​​R.; Marrett, Sean; Ungerleider, Leslie G. (9 de mayo de 2008). "Los sistemas neuronales que median en la toma de decisiones perceptivas humanas". Reseñas de la naturaleza Neurociencia . 9 (6): 467–479. doi :10.1038/nrn2374. PMID  18464792. S2CID  7416645.
22. Costa, VD; Averbeck, BB (18 de octubre de 2013). "La actividad frontal-parietal y límbico-estriatal es la base del muestreo de información en el problema de la mejor elección". Corteza cerebral . 25 (4): 972–982. doi :10.1093/cercor/bht286. PMC 4366612 . PMID  24142842. 
23. Inundación de 1958.
24. Gardner 1966, Problema 3.
25. Brus 1984.
26. Ferguson 1989.
27. Kesselheim, Thomas; Radke, Klaus; Tönnis, Andreas; Vöcking, Berthold (2013). "Un algoritmo en línea óptimo para la comparación bipartita ponderada y extensiones de subastas combinatorias". Algoritmos – ESA 2013 . Apuntes de conferencias sobre informática. vol. 8125, págs. 589–600. doi :10.1007/978-3-642-40450-4_50. ISBN 978-3-642-40449-8.

Referencias

• Bearden, JN (2006). "Un nuevo problema de secretaria con selección basada en rangos y pagos cardinales". Revista de Psicología Matemática . 50 : 58–9. doi :10.1016/j.jmp.2005.11.003.
• Bearden, JN; Murphy, RO; Rapoport, A. (2005). "Una extensión de atributos múltiples del problema de la secretaria: teoría y experimentos". Revista de Psicología Matemática . 49 (5): 410–425. CiteSeerX  10.1.1.497.6468 . doi :10.1016/j.jmp.2005.08.002. S2CID  9186039.
• Bearden, J. Neil; Rapoport, Amnón; Murphy, Ryan O. (septiembre de 2006). "Observación secuencial y selección con resultados dependientes del rango: un estudio experimental". Ciencias de la gestión . 52 (9): 1437-1449. doi :10.1287/mnsc.1060.0535.
• Bruss, F. Thomas (junio de 2000). "Sume las probabilidades a uno y deténgase". Los anales de la probabilidad . 28 (3): 1384-1391. doi : 10.1214/aop/1019160340 .
• Bruss, F. Thomas (octubre de 2003). "Una nota sobre los límites del teorema de probabilidades de parada óptima". Los anales de la probabilidad . 31 (4): 1859-1961. doi : 10.1214/aop/1068646368 .
• Bruss, F. Thomas (agosto de 1984). "Un enfoque unificado para una clase de problemas de mejor elección con un número desconocido de opciones". Los anales de la probabilidad . 12 (3): 882–889. doi : 10.1214/aop/1176993237 .
• Inundación, Merrill R. (1958). "Prueba de la estrategia óptima". Carta a Martín Gardner. Artículos de Martin Gardner serie 1, cuadro 5, carpeta 19: Archivos de la Universidad de Stanford.{{cite press release}}: CS1 maint: location (link)
• Freeman, PR (1983). "El problema de la secretaria y sus extensiones: una revisión". Revista estadística internacional/Revue Internationale de Statistique . 51 (2): 189–206. doi :10.2307/1402748. JSTOR  1402748.
• Gardner, Martín (1966). "3". Nuevas desviaciones matemáticas de Scientific American . Simón y Schuster.[reimprime su columna original publicada en febrero de 1960 con comentarios adicionales]
• Girdhar, Yogesh; Dudek, Gregorio (2009). "Muestreo óptimo de datos en línea o cómo contratar a las mejores secretarias". Conferencia canadiense de 2009 sobre visión por computadora y robot . págs. 292–298. CiteSeerX  10.1.1.161.41 . doi :10.1109/CRV.2009.30. ISBN 978-1-4244-4211-9. S2CID  2742443.
• Gilbert, J; Mosteller, F (1966). "Reconocer el máximo de una secuencia". Revista de la Asociación Estadounidense de Estadística . 61 (313): 35–73. doi :10.2307/2283044. JSTOR  2283044.
• Gnedin, A. (1994). "Una solución al juego de Googol". Anales de probabilidad . 22 (3): 1588-1595. doi : 10.1214/aop/1176988613 .
• Gnedin, A. (2021). "El problema de la mejor elección con llegadas aleatorias: cómo superar la estrategia 1/e". Procesos estocásticos y sus aplicaciones . 145 : 226–240. doi :10.1016/j.spa.2021.12.008. S2CID  245449000.
• Hill, TP "Saber cuándo parar". Científico estadounidense , vol. 97, 126-133 (2009). (Para la traducción al francés, consulte el artículo de portada de la edición de julio de Pour la Science (2009))
• Ketelaar, Timoteo; Todd, Peter M. (2001). "Enmarcar nuestros pensamientos: la racionalidad ecológica como respuesta de la psicología evolutiva al problema del marco". Desafíos conceptuales en psicología evolutiva . Estudios en Sistemas Cognitivos. vol. 27. págs. 179-211. doi :10.1007/978-94-010-0618-7_7. ISBN 978-94-010-3890-4.
• Matsui, T; Año, K (2016). "Límites inferiores para el problema de probabilidades de Bruss con múltiples detenciones". Matemáticas de la Investigación de Operaciones . 41 (2): 700–714. arXiv : 1204.5537 . doi :10.1287/moor.2015.0748. S2CID  31778896.
• Molinero, Geoffrey F. (2001). La mente de apareamiento: cómo la elección sexual dio forma a la evolución de la naturaleza humana . Libros ancla. ISBN 978-0-385-49517-2.
• Sardelis, Dimitris A.; Valahas, Theodoros M. (marzo de 1999). "Toma de decisiones: una regla de oro". El Mensual Matemático Estadounidense . 106 (3): 215. doi : 10.2307/2589677. JSTOR  2589677.
• Seale, DA; Rapoport, A. (1997). "Toma de decisiones secuencial con rangos relativos: una investigación experimental del 'problema de la secretaria'". Comportamiento organizacional y procesos de decisión humana . 69 (3): 221–236. doi :10.1006/obhd.1997.2683.
• Stein, NOSOTROS; Seale, DA; Rapoport, A. (2003). "Análisis de soluciones heurísticas al problema de la mejor elección". Revista europea de investigación operativa . 151 : 140-152. doi :10.1016/S0377-2217(02)00601-X.
• Vanderbei, RJ (noviembre de 1980). "La elección óptima de un subconjunto de una población". Matemáticas de la Investigación de Operaciones . 5 (4): 481–486. doi :10.1287/moor.5.4.481.
• Vanderbei, Robert J. (2012). La variante postdoctoral del problema de la secretaria (PDF) (Reporte). CiteSeerX  10.1.1.366.1718 .

enlaces externos

• Secuencia OEIS A054404 (Número de hijas que deben esperar antes de abordar el problema de la dote del sultán con n hijas)
• Weisstein, Eric W. "El problema de la dote del sultán". MundoMatemático .
• Neil Bearden. "Búsqueda óptima (problemas de secretaria)". Archivado desde el original el 4 de enero de 2017.
• Libro de aplicaciones y parada óptima de Thomas S. Ferguson

Notas

1. importar  numpy  como  np importar  pandas  como  pd# Defina la función para la cual desea encontrar la función de definición máxima  ( r , n ): si r == 1 : devuelve 0, de lo contrario : devuelve ( r - 1 ) / n * np . suma ([ 1 / ( i - 1 ) para i en el rango ( r , n + 1 )])                         # Definir una función para resolver el problema para un n específico resolver  ( n ): valores = [ func ( r , n ) para r en el rango ( 1 , n + 1 ) ] r_max = np . argmax ( valores ) + 1 devuelve r_max , valores [ r_max - 1 ]                   # Definir una función para imprimir los resultados como una tabla Markdown def  print_table ( n_max ):  # Preparar datos para la tabla  data  =  [ solve ( n )  for  n  in  range ( 1 ,  n_max + 1 )]  df  =  pd . Marco de datos ( datos ,  columnas = [ 'r' ,  'Valor máximo' ],  índice = rango ( 1 ,  n_max + 1 ))  df . índice . nombre  =  'n'  # Convierta el DataFrame a Markdown e imprima  print ( df . transpose () . to_markdown ())# Imprime la tabla para n del 1 al 10 print_table ( 10 )