
Las reglas de Woodward-Hoffmann (o reglas de selección pericíclica ) [1] son un conjunto de reglas ideadas por Robert Burns Woodward y Roald Hoffmann para racionalizar o predecir ciertos aspectos de la estereoquímica y la energía de activación de las reacciones pericíclicas , una clase importante de reacciones en la química orgánica . Las reglas se originan en ciertas simetrías de la estructura orbital de la molécula que cualquier hamiltoniano molecular conserva . En consecuencia, cualquier reacción que viole la simetría debe acoplarse ampliamente con el entorno ; esto impone una barrera de energía a su ocurrencia, y tales reacciones se denominan simetría-prohibida . Sus opuestos son simetría-permitida .
Aunque la barrera impuesta por la simetría es a menudo formidable (hasta ca. 5 eV o 480 kJ/mol en el caso de una cicloadición [2+2] prohibida), la prohibición no es absoluta, y las reacciones prohibidas por la simetría aún pueden tener lugar si otros factores (por ejemplo, liberación de tensión) favorecen la reacción. Del mismo modo, una reacción permitida por la simetría puede ser prevenida por una barrera energética infranqueable resultante de factores no relacionados con la simetría orbital. Todos los casos conocidos solo violan las reglas superficialmente; en cambio, diferentes partes del mecanismo se vuelven asincrónicas , y cada paso se ajusta a las reglas.
Una reacción pericíclica es una reacción orgánica que procede a través de un único estado de transición cíclico y concertado , cuya geometría permite la superposición continua de un ciclo de orbitales (π y/o σ) .
Los términos conrotatorio y disrotatorio describen el sentido relativo de la rotación del enlace que interviene en las reacciones electrocíclicas de apertura y cierre de anillos. En un proceso disrotatorio, los dos extremos del enlace que se rompe o se forma giran en direcciones opuestas (uno en el sentido de las agujas del reloj, otro en el sentido contrario a las agujas del reloj); en un proceso conrotatorio, giran en la misma dirección (ambos en el sentido de las agujas del reloj o ambos en el sentido contrario a las agujas del reloj), el proceso es conrotatorio .

Finalmente, se reconoció que las reacciones pericíclicas promovidas térmicamente en general obedecen a un único conjunto de reglas de selección generalizadas, dependiendo del recuento de electrones y la topología de las interacciones orbitales. El concepto clave de topología orbital o facialidad se introdujo para unificar varias clases de reacciones pericíclicas bajo un único marco conceptual. En resumen, un conjunto de átomos contiguos y sus orbitales asociados que reaccionan como una unidad en una reacción pericíclica se conoce como un componente , y se dice que cada componente es antarafacial o suprafacial dependiendo de si los lóbulos orbitales que interactúan durante la reacción están en el lado opuesto o en el mismo lado del plano nodal, respectivamente. (Los términos más antiguos conrotatorio y disrotatorio, que son aplicables solo a la apertura y cierre de anillos electrocíclicos, están subsumidos por los términos antarafacial y suprafacial, respectivamente, bajo este sistema de clasificación más general).
Woodward y Hoffmann desarrollaron las reglas de selección pericíclica después de realizar cálculos extensos de superposición orbital. En ese momento, Woodward quería saber si ciertas reacciones electrocíclicas podrían ayudar a sintetizar vitamina B 12 . Los químicos sabían que tales reacciones exhibían una estereoespecificidad sorprendente, pero no podían predecir qué estereoisómero podría seleccionar una reacción. En 1965, Woodward-Hoffmann se dio cuenta de que un conjunto simple de reglas explicaba la estereoespecificidad observada en los extremos de los polienos conjugados de cadena abierta cuando se calentaban o irradiaban. En su publicación original, [2] resumieron la evidencia experimental y el análisis de orbitales moleculares de la siguiente manera:
En 1969, utilizarían diagramas de correlación para enunciar una regla de selección pericíclica generalizada equivalente a la que ahora lleva su nombre: se permite una reacción pericíclica si la suma del número de componentes suprafaciales 4 q + 2 y el número de componentes antarafaciales 4 r es impar.
En los cuatro años intermedios, Howard Zimmerman [3] [4] y Michael JS Dewar [5] [6] propusieron un marco conceptual igualmente general: el concepto de Möbius-Hückel o teoría del estado de transición aromático . En el enfoque de Dewar-Zimmerman, la topología de superposición orbital (Hückel o Möbius) y el recuento de electrones (4 n + 2 o 4 n ) dan como resultado un estado de transición aromático o antiaromático.
Mientras tanto, Kenichi Fukui [7] [8] analizó los orbitales de frontera de tales sistemas. Un proceso en el que la interacción HOMO-LUMO es constructiva (resulta en una interacción de enlace neto) es favorable y se considera permitido por la simetría, mientras que un proceso en el que la interacción HOMO-LUMO no es constructiva (resulta en interacciones de enlace y antienlace que se cancelan) es desfavorable y se considera prohibido por la simetría.
Aunque conceptualmente distintas, la teoría del estado de transición aromático (Zimmerman y Dewar), la teoría de los orbitales moleculares de frontera (Fukui) y la conservación de la simetría orbital (Woodward y Hoffmann) hacen predicciones idénticas. Las reglas de Woodward-Hoffmann ejemplifican el poder de la teoría de los orbitales moleculares [9] y, de hecho, ayudaron a demostrar que podrían surgir resultados químicos útiles del análisis orbital. El descubrimiento le valió a Hoffmann y Fukui el Premio Nobel de Química de 1981 [10] . Para entonces, Woodward ya había fallecido y, por lo tanto, no podía optar al premio.
La interconversión de derivados modelo de ciclobuteno y butadieno en condiciones térmicas (calentamiento) y fotoquímicas ( irradiación ultravioleta ) es ilustrativa.
Las reglas de Woodward-Hoffmann se aplican en ambas direcciones de un proceso pericíclico. Debido a la tensión de anillo inherente de los derivados del ciclobuteno, el equilibrio entre el ciclobuteno y el 1,3-butadieno se encuentra muy a la derecha. Por lo tanto, en condiciones térmicas, la apertura del anillo del ciclobuteno al 1,3-butadieno se ve fuertemente favorecida por la termodinámica. Por otro lado, bajo la irradiación con luz ultravioleta, se alcanza un estado fotoestacionario , una composición que depende tanto de la absorbancia como del rendimiento cuántico de las reacciones directa e inversa a una longitud de onda particular. Debido a los diferentes grados de conjugación de los 1,3-butadienos y los ciclobutenos, solo el 1,3-butadieno tendrá una absorbancia significativa a longitudes de onda más altas, suponiendo la ausencia de otros cromóforos. Por lo tanto, la irradiación del 1,3-butadieno a esa longitud de onda puede dar como resultado una alta conversión al ciclobuteno. La termólisis del trans -1,2,3,4-tetrametil-1-ciclobuteno ( 1 ) proporcionó solo un isómero geométrico, ( E , E )-3,4-dimetil-2,4-hexadieno ( 2 ); los isómeros geométricos ( Z , Z ) y ( E , Z ) no se detectaron en la mezcla de productos. De manera similar, la termólisis del cis -1,2,3,4-tetrametil-1-ciclobuteno ( 3 ) proporcionó solo el isómero ( E , Z ) 4 . [11] En ambas reacciones de apertura de anillo, los carbonos en los extremos del enlace σ de ruptura giran en la misma dirección. [12] Por otra parte, se siguió el curso estereoquímico opuesto bajo activación fotoquímica: cuando el compuesto relacionado ( E , E )-2,4-hexadieno ( 5 ) se expuso a la luz, se formó cis -3,4-dimetil-1-ciclobuteno ( 6 ) exclusivamente como resultado del cierre del anillo electrocíclico. [13] Esto requiere que los extremos del sistema π roten en direcciones opuestas para formar el nuevo enlace σ. La termólisis de 6 sigue el mismo curso estereoquímico que 3 : la apertura del anillo electrocíclico conduce a la formación de ( E , Z )-2,4-hexadieno ( 7 ) y no de 5 . [14]

Las reglas de Woodward-Hoffmann explican estos resultados a través de la superposición orbital:
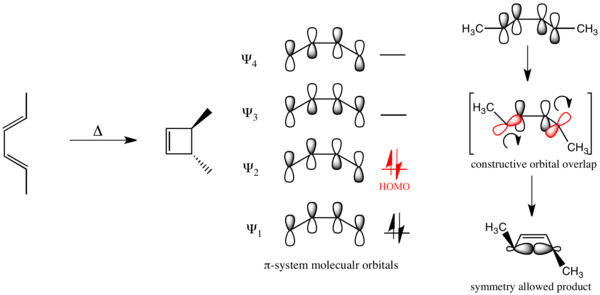
En el caso de un cierre de anillo electrocíclico impulsado fotoquímicamente del buta-1,3-dieno, la promoción electrónica hace que se convierta en HOMO y el mecanismo de reacción debe ser disrotatorio.
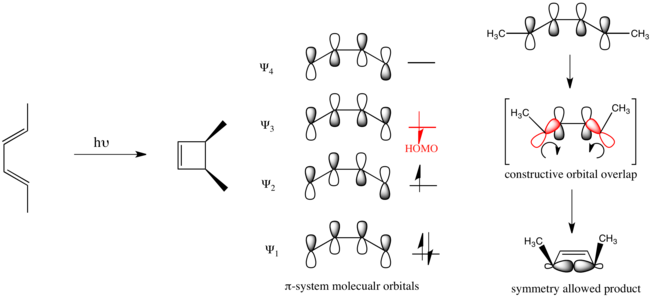
Por el contrario, en el cierre de anillo electrocíclico del hexa-1,3,5-trieno sustituido que se muestra a continuación, la reacción se desarrolla a través de un mecanismo disrotatorio.

Las reglas de Woodward-Hoffmann se pueden resumir sucintamente en una sola frase: [15]
Regla de selección pericíclica generalizada. Un proceso pericíclico en estado fundamental que involucra N pares de electrones y A componentes antarafaciales tiene simetría permitida si y solo si N + A es impar.
Un proceso pericíclico en estado fundamental se produce mediante la adición de energía térmica (es decir, calentando el sistema, simbolizado por Δ ). Por el contrario, un proceso pericíclico en estado excitado tiene lugar si un reactivo se promueve a un estado electrónicamente excitado mediante la activación con luz ultravioleta (es decir, irradiando el sistema, simbolizado por h ν ). Sin embargo, es importante reconocer que el mecanismo operativo de una reacción formalmente pericíclica que tiene lugar bajo irradiación fotoquímica generalmente no es tan simple o claro como sugiere esta dicotomía. Por lo general, son posibles varios modos de excitación electrónica, y las moléculas excitadas electrónicamente pueden experimentar un cruce entre sistemas , una desintegración sin radiación o relajarse hasta una geometría de equilibrio desfavorable antes de que pueda tener lugar el proceso pericíclico en estado excitado. Por lo tanto, se piensa que muchas reacciones pericíclicas aparentes que tienen lugar bajo irradiación son en realidad procesos escalonados que involucran intermediarios dirradicales. Sin embargo, con frecuencia se observa que las reglas de selección pericíclica se invierten cuando se cambia de activación térmica a fotoquímica. Esto se puede racionalizar considerando la correlación de los primeros estados electrónicos excitados de los reactivos y productos. Aunque se trata más de una heurística útil que de una regla, se puede enunciar un principio de selección generalizado correspondiente para las reacciones pericíclicas fotoquímicas:
Un proceso pericíclico que involucra pares de electrones N y componentes antarafaciales A suele verse favorecido en condiciones fotoquímicas si N + A es par.
También se conocen reacciones pericíclicas en las que interviene un número impar de electrones. Con respecto a la aplicación de la regla generalizada de selección pericíclica, estos sistemas pueden tratarse generalmente como si estuviera implicado un electrón más. [16]
En el lenguaje de la teoría del estado de transición aromático, las reglas de Woodward-Hoffmann se pueden reformular de la siguiente manera: un estado de transición pericíclico que involucra (4 n + 2) electrones con topología de Hückel o 4 n electrones con topología de Möbius es aromático y permitido, mientras que un estado de transición pericíclico que involucra 4 n -electrones con topología de Hückel o (4 n + 2)-electrones con topología de Möbius es antiaromático y prohibido.
Longuet-Higgins y EW Abrahamson demostraron que las reglas de Woodward-Hoffmann se pueden derivar mejor examinando el diagrama de correlación de una reacción dada. [17] [16] [18] [19] Un elemento de simetría es un punto de referencia (generalmente un plano o una línea) sobre el cual un objeto es simétrico con respecto a una operación de simetría. Si un elemento de simetría está presente en todo el mecanismo de reacción (reactivo, estado de transición y producto), se denomina elemento de simetría conservado. Entonces, a lo largo de la reacción, la simetría de los orbitales moleculares con respecto a este elemento debe conservarse. Es decir, los orbitales moleculares que son simétricos con respecto al elemento de simetría en el material de partida deben correlacionarse con orbitales (transformarse en) simétricos con respecto a ese elemento en el producto. A la inversa, la misma afirmación se aplica a la antisimetría con respecto a un elemento de simetría conservado. Un diagrama de correlación de orbitales moleculares correlaciona los orbitales moleculares de los materiales de partida y el producto basándose en la conservación de la simetría. A partir de un diagrama de correlación de orbitales moleculares se puede construir un diagrama de correlación de estados electrónicos que correlaciona los estados electrónicos (es decir, el estado fundamental y los estados excitados) de los reactivos con los estados electrónicos de los productos. Los diagramas de correlación se pueden utilizar para predecir la altura de las barreras de estados de transición. [20]
Aunque la "simetría" orbital se utiliza como una herramienta para esbozar diagramas de correlación orbital y de estado, la presencia o ausencia absoluta de un elemento de simetría no es crítica para la determinación de si una reacción está permitida o prohibida. Es decir, la introducción de un sustituyente simple que interrumpe formalmente un plano o eje de simetría (por ejemplo, un grupo metilo) generalmente no afecta la evaluación de si una reacción está permitida o prohibida. En cambio, la simetría presente en un análogo no sustituido se utiliza para simplificar la construcción de diagramas de correlación orbital y evitar la necesidad de realizar cálculos. [21] Solo las relaciones de fase entre orbitales son importantes al juzgar si una reacción está "simétricamente" permitida o prohibida. Además, aún se pueden realizar correlaciones orbitales, incluso si no hay elementos de simetría conservados (por ejemplo, desplazamientos 1,5-sigmatrópicos y reacciones eno). Por esta razón, los análisis de Woodward-Hoffmann, Fukui y Dewar-Zimmerman son igualmente amplios en su aplicabilidad, aunque un determinado enfoque puede ser más fácil o más intuitivo de aplicar que otro, dependiendo de la reacción que se desee analizar.


Considerando el cierre del anillo electrocíclico del 1,3-butadieno sustituido, la reacción puede proceder a través de un mecanismo de reacción conrotatorio o disrotatorio . Como se muestra a la izquierda, en el estado de transición conrotatorio hay un eje de simetría C2 y en el estado de transición disrotatorio hay un plano de simetría especular σ . Para correlacionar los orbitales del material de partida y del producto, se debe determinar si los orbitales moleculares son simétricos o antisimétricos con respecto a estos elementos de simetría. Los orbitales moleculares del sistema π del butadieno se muestran a la derecha junto con el elemento de simetría con el que son simétricos. Son antisimétricos con respecto al otro. Por ejemplo, Ψ2 del 1,3-butadieno es simétrico con respecto a la rotación de 180 ° alrededor del eje C2 y antisimétrico con respecto a la reflexión en el plano especular.
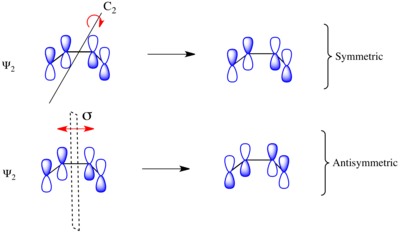
Ψ 1 y Ψ 3 son simétricos con respecto al plano especular, ya que el signo de los lóbulos orbitales p se conserva bajo la transformación de simetría. De manera similar, Ψ 1 y Ψ 3 son antisimétricos con respecto al eje C 2 , ya que la rotación invierte el signo de los lóbulos orbitales p de manera uniforme. Por el contrario, Ψ 2 y Ψ 4 son simétricos con respecto al eje C 2 y antisimétricos con respecto al plano especular σ.

El mismo análisis se puede realizar para los orbitales moleculares del ciclobuteno. El resultado de ambas operaciones de simetría en cada uno de los orbitales moleculares se muestra a la izquierda. Como los orbitales σ y σ * se encuentran completamente en el plano que contiene C 2 perpendicular a σ, son uniformemente simétricos y antisimétricos (respectivamente) con respecto a ambos elementos de simetría. Por otro lado, π es simétrico con respecto a la reflexión y antisimétrico con respecto a la rotación, mientras que π * es antisimétrico con respecto a la reflexión y simétrico con respecto a la rotación.
Se trazan líneas de correlación para conectar los orbitales moleculares en el material de partida y el producto que tienen la misma simetría con respecto al elemento de simetría conservado. En el caso del cierre de anillo electrocíclico conrotatorio de 4 electrones del 1,3-butadieno, el orbital molecular más bajo Ψ 1 es asimétrico (A) con respecto al eje C 2 . Por lo tanto, este orbital molecular está correlacionado con el orbital π del ciclobuteno, el orbital de energía más baja que también es (A) con respecto al eje C 2 . De manera similar, Ψ 2 , que es simétrico (S) con respecto al eje C 2 , está correlacionado con σ del ciclobuteno. Las dos correlaciones finales son entre los orbitales moleculares antisimétricos (A) Ψ 3 y σ * , y los orbitales moleculares simétricos (S) Ψ 4 y π * . [16]

De manera similar, existe un diagrama de correlación para un mecanismo disrotatorio. En este mecanismo, el elemento de simetría que persiste a lo largo de todo el mecanismo es el plano de reflexión σ. Aquí, el orbital molecular de menor energía Ψ 1 del 1,3-butadieno es simétrico con respecto al plano de reflexión y, como tal, se correlaciona con el orbital molecular σ simétrico del ciclobuteno. De manera similar, el par de orbitales moleculares simétricos de mayor energía Ψ 3 y π se correlacionan. En cuanto a los orbitales moleculares asimétricos, el par de menor energía Ψ 2 y π * forman un par de correlación, al igual que Ψ 4 y σ * . [16]

Al evaluar los dos mecanismos, se predice que el mecanismo conrotatorio tiene una barrera más baja porque transforma los electrones de los orbitales del estado fundamental de los reactivos (Ψ 1 y Ψ 2 ) en orbitales del estado fundamental del producto (σ y π). Por el contrario, el mecanismo disrotatorio fuerza la conversión del orbital Ψ 1 en el orbital σ, y del orbital Ψ 2 en el orbital π * . Por lo tanto, los dos electrones en el orbital Ψ 2 del estado fundamental se transfieren a un orbital antienlazante excitado, creando un estado electrónico doblemente excitado del ciclobuteno. Esto conduciría a una barrera de estado de transición significativamente más alta para la reacción. [16]

Sin embargo, como las reacciones no tienen lugar entre orbitales moleculares disjuntos, sino entre estados electrónicos, el análisis final implica diagramas de correlación de estados. Un diagrama de correlación de estados correlaciona la simetría general de los estados electrónicos en el material de partida y el producto. El estado fundamental del 1,3-butadieno, como se muestra arriba, tiene 2 electrones en Ψ 1 y 2 electrones en Ψ 2 , por lo que se representa como Ψ 1 2 Ψ 2 2 . La simetría general del estado es el producto de las simetrías de cada orbital lleno con multiplicidad para orbitales doblemente poblados. Por lo tanto, como Ψ 1 es asimétrico con respecto al eje C 2 , y Ψ 2 es simétrico, el estado total se representa por A 2 S 2 . Para ver por qué este producto particular es matemáticamente S en general, que S se puede representar como (+1) y A como (−1). Esto se deriva del hecho de que los signos de los lóbulos de los orbitales p se multiplican por (+1) si son simétricos con respecto a una transformación de simetría (es decir, inalterados) y se multiplican por (−1) si son antisimétricos con respecto a una transformación de simetría (es decir, invertidos). Por lo tanto, A 2 S 2 =(−1) 2 (+1) 2 =+1=S. El primer estado excitado (ES-1) se forma al promover un electrón del HOMO al LUMO , y por lo tanto se representa como Ψ 1 2 Ψ 2 Ψ 3. Como Ψ 1 es A, Ψ 2 es S y Ψ 3 es A, la simetría de este estado está dada por A 2 SA=A. Ahora, considerando los estados electrónicos del producto, ciclobuteno, el estado fundamental está dado por σ 2 π 2 , que tiene simetría S 2 A 2 =S. El primer estado excitado (ES-1') se forma nuevamente a partir de una promoción de un electrón del HOMO al LUMO , por lo que en este caso se representa como σ 2 ππ * . La simetría de este estado es S 2 AS=A.
El estado fundamental Ψ 1 2 Ψ 2 2 del 1,3-butadieno se correlaciona con el estado fundamental σ 2 π 2 del ciclobuteno, como se demuestra en el diagrama de correlación de OM anterior. Ψ 1 se correlaciona con π y Ψ 2 se correlaciona con σ. Por lo tanto, los orbitales que forman Ψ 1 2 Ψ 2 2 deben transformarse en los orbitales que forman σ 2 π 2 bajo un mecanismo conrotatorio. Sin embargo, el estado ES-1 no se correlaciona con el estado ES-1' ya que los orbitales moleculares no se transforman entre sí bajo el requisito de simetría visto en el diagrama de correlación de orbitales moleculares. En cambio, como Ψ 1 se correlaciona con π, Ψ 2 se correlaciona con σ y Ψ 3 se correlaciona con σ * , el estado Ψ 1 2 Ψ 2 Ψ 3 intenta transformarse en π 2 σσ * , que es un estado excitado diferente. Entonces ES-1 intenta correlacionarse con ES-2'=σπ 2 σ * , que es más alto en energía que Es-1'. De manera similar, ES-1'=σ 2 ππ * intenta correlacionarse con ES-2=Ψ 1 Ψ 2 2 Ψ 4 . Estas correlaciones no pueden tener lugar realmente debido a la regla mecánico-cuántica conocida como la regla de cruce evitado . Esta dice que las configuraciones energéticas de la misma simetría no pueden cruzarse en un diagrama de correlación de niveles de energía. En resumen, esto es causado por la mezcla de estados de la misma simetría cuando se acercan lo suficiente en energía. Por lo tanto, se forma una barrera de alta energía entre una transformación forzada de ES-1 en ES-1'. En el diagrama siguiente, las correlaciones preferidas por la simetría se muestran en líneas discontinuas y las líneas curvas en negrita indican la correlación real con la barrera de alta energía. [16] [20]

El mismo análisis se puede aplicar al mecanismo disrotatorio para crear el siguiente diagrama de correlación de estados. [16] [20]

Por lo tanto, si la molécula está en el estado fundamental, procederá a través del mecanismo conrotatorio (es decir, bajo control térmico) para evitar una barrera electrónica. Sin embargo, si la molécula está en el primer estado excitado (es decir, bajo control fotoquímico), la barrera electrónica está presente en el mecanismo conrotatorio y la reacción procederá a través del mecanismo disrotatorio. Estos no son completamente distintos ya que tanto el mecanismo conrotatorio como el disrotatorio se encuentran en la misma superficie potencial. Por lo tanto, una afirmación más correcta es que, a medida que una molécula en estado fundamental explora la superficie de energía potencial, es más probable que alcance la barrera de activación para someterse a un mecanismo conrotatorio. [20]
Las reglas de Woodward-Hoffmann también pueden explicar las reacciones de cicloadición bimolecular a través de diagramas de correlación. [22] Una cicloadición [ π p + π q ] reúne dos componentes, uno con p electrones π y el otro con q electrones π. Las reacciones de cicloadición se caracterizan además como suprafaciales (s) o antarafaciales (a) con respecto a cada uno de los componentes π. ( Véase más abajo "Formulación general" para una descripción detallada de la generalización de la notación WH a todos los procesos pericíclicos ).
Para los alquenos ordinarios, las cicloadiciones [2+2] sólo se observan bajo activación fotoquímica.
La justificación para la no observación de cicloadiciones térmicas [2+2] comienza con el análisis de las cuatro posibles consecuencias estereoquímicas para la cicloadición [2+2]: [ π 2 s + π 2 s ], [ π 2 a + π 2 s ], [ π 2 s + π 2 a ], [ π 2 a + π 2 a ]. El modo geométricamente más plausible [ π 2 s + π 2 s ] está prohibido bajo condiciones térmicas, mientras que los enfoques [ π 2 a + π 2 s ], [ π 2 s + π 2 a ] están permitidos desde el punto de vista de la simetría pero son raros debido a una deformación y un perfil estérico desfavorables. [16]


Considerando la cicloadición [ π 2 s + π 2 s ]. Este mecanismo conduce a una retención de la estereoquímica en el producto, como se ilustra a la derecha. Dos elementos de simetría están presentes en los materiales de partida, el estado de transición y el producto: σ 1 y σ 2 . σ 1 es el plano especular entre los componentes perpendiculares a los orbitales p ; σ 2 divide las moléculas por la mitad perpendicularmente a los enlaces σ . [22] Ambos son elementos de simetría local en el caso de que los componentes no sean idénticos.

Para determinar la simetría y asimetría con respecto a σ 1 y σ 2 , los orbitales moleculares del material de partida deben considerarse en tándem. La figura de la derecha muestra el diagrama de correlación de orbitales moleculares para la cicloadición [ π 2 s + π 2 s ]. Los dos orbitales moleculares π y π * de los materiales de partida se caracterizan por su simetría con respecto primero a σ 1 y luego a σ 2 . De manera similar, los orbitales moleculares σ y σ * del producto se caracterizan por su simetría. En el diagrama de correlación, las transformaciones de orbitales moleculares a lo largo de la reacción deben conservar la simetría de los orbitales moleculares. Por lo tanto, π SS se correlaciona con σ SS , π AS se correlaciona con σ * AS , π * SA se correlaciona con σ SA y, finalmente, π * AA se correlaciona con σ * AA . Debido a la conservación de la simetría orbital, el orbital de enlace π AS se ve obligado a correlacionarse con el orbital de antienlace σ * AS . Por lo tanto, se predice una barrera alta. [16] [20] [22]
Esto se hace preciso en el diagrama de correlación de estados a continuación. [16] [20] El estado fundamental en los materiales de partida es el estado electrónico donde π SS y π AS están doblemente poblados, es decir, el estado (SS) 2 (AS) 2 . Como tal, este estado intenta correlacionarse con el estado electrónico en el producto donde tanto σ SS como σ * AS están doblemente poblados, es decir, el estado (SS) 2 (AS) 2 . Sin embargo, este estado no es el estado fundamental (SS) 2 (SA) 2 del ciclobutano, ni el primer estado excitado ES-1'=(SS) 2 (SA)(AS), donde un electrón es promovido del HOMO al LUMO.

La reacción de Diels-Alder ejemplifica una cicloadición [4+2] . El caso más simple es la reacción del 1,3-butadieno con etileno para formar ciclohexeno .
En esta transformación se conserva un elemento de simetría: el plano especular que pasa por el centro de los reactivos, como se muestra a la izquierda. Los orbitales moleculares de los reactivos son el conjunto {Ψ 1 , Ψ 2 , Ψ 3 , Ψ 4 } de orbitales moleculares del 1,3-butadieno que se muestran arriba, junto con π y π * del etileno. Ψ 1 es simétrico, Ψ 2 es antisimétrico, Ψ 3 es simétrico y Ψ 4 es antisimétrico con respecto al plano especular. De manera similar, π es simétrico y π * es antisimétrico con respecto al plano especular.

Los orbitales moleculares del producto son las combinaciones simétricas y antisimétricas de los dos enlaces recién formados σ y σ * y los enlaces π y π * como se muestra a continuación.
La correlación de los pares de orbitales en los materiales de partida y el producto de la misma simetría y energía creciente da como resultado el diagrama de correlación de la derecha. Como esto transforma los orbitales moleculares de enlace del estado fundamental de los materiales de partida en los orbitales de enlace del estado fundamental del producto de una manera que conserva la simetría, se predice que no habrá una gran barrera energética presente en la reacción del estado fundamental [2+2] anterior.
Para hacer el análisis preciso, se puede construir el diagrama de correlación de estados para la cicloadición general [4+2]. [20] Como antes, el estado fundamental es el estado electrónico representado en el diagrama de correlación de orbitales moleculares a la derecha. Este se puede describir como Ψ 1 2 π 2 Ψ 2 2 , de simetría total S 2 S 2 A 2 =S. Esto se correlaciona con el estado fundamental del ciclohexeno σ S σ A π 2 que también es S 2 S 2 A 2 =S. Como tal, no se predice que esta reacción de estado fundamental tenga una alta barrera impuesta por la simetría.
También se pueden construir las correlaciones de estado excitado como se hizo anteriormente. Aquí, hay una barrera energética alta para una reacción de Diels-Alder fotoinducida bajo una topología de enlace suprafacial-suprafacial debido al cruce evitado que se muestra a continuación.


Las alturas de barrera impuestas por la simetría de las reacciones de transferencia de grupos también se pueden analizar utilizando diagramas de correlación. Una reacción modelo es la transferencia de un par de átomos de hidrógeno del etano al perdeuterioetileno, que se muestra a la derecha.
El único elemento de simetría conservado en esta reacción es el plano especular que pasa por el centro de las moléculas, como se muestra a la izquierda.

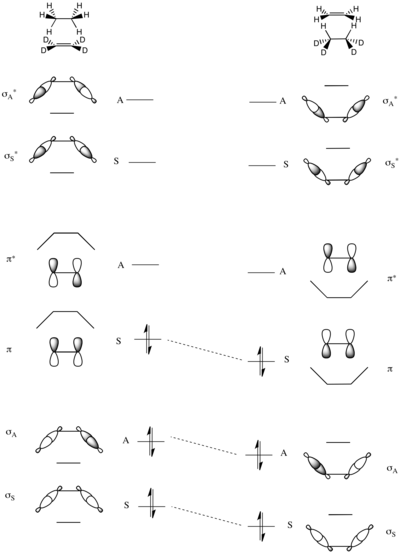
Los orbitales moleculares del sistema se construyen como combinaciones simétricas y antisimétricas de enlaces σ y σ * C–H en etano y enlaces π y π * en el eteno deutero-sustituido. Por lo tanto, el OM de energía más baja es la suma simétrica de los dos enlaces σ C–H (σ S ), seguida de la suma antisimétrica (σ A ). Los dos OM de energía más alta se forman a partir de combinaciones lineales de los antienlaces σ CH – el más alto es el antisimétrico σ * A , precedido por el simétrico σ * A a una energía ligeramente menor. En el medio de la escala energética están los dos OM restantes que son el π CC y el π * CC del eteno.
El diagrama de correlación de orbitales moleculares completo se construye haciendo coincidir pares de orbitales moleculares simétricos y asimétricos de energía total creciente, como se explicó anteriormente. Como se puede ver en el diagrama adyacente, como los orbitales de enlace de los reactivos se correlacionan exactamente con los orbitales de enlace de los productos, no se predice que esta reacción tenga una barrera impuesta por una alta simetría electrónica. [16] [20]
Utilizando diagramas de correlación se pueden derivar reglas de selección para las siguientes clases generalizadas de reacciones pericíclicas. Cada una de estas clases particulares se generaliza aún más en las reglas generalizadas de Woodward-Hoffmann. Los descriptores de topología de enlace más inclusivos antarafacial y suprafacial incluyen los términos conrotatorio y disrotatorio, respectivamente. Antarafacial se refiere a la formación o ruptura de enlaces a través de la cara opuesta de un sistema π, orbital p o enlace σ, mientras que suprafacial se refiere al proceso que ocurre a través de la misma cara. Una transformación suprafacial en un centro quiral preserva la estereoquímica, mientras que una transformación antarafacial revierte la estereoquímica.
La regla de selección de las reacciones de electrociclación se da en el enunciado original de las reglas de Woodward-Hoffmann. Si se produce un cierre de anillo electrocíclico generalizado en un polieno de 4 n π-electrones, entonces es conrotatorio en condiciones térmicas y disrotatorio en condiciones fotoquímicas. Por el contrario, en un polieno de 4 n + 2 π-electrones, un cierre de anillo electrocíclico es disrotatorio en condiciones térmicas y conrotatorio en condiciones fotoquímicas.
Este resultado puede derivarse mediante un análisis FMO basado en el signo de los lóbulos orbitales p del HOMO del polieno o con diagramas de correlación. Tomando primero la primera posibilidad, en el estado fundamental, si un polieno tiene 4 electrones n , los orbitales p externos del HOMO que forman el enlace σ en el producto electrociclado son de signos opuestos. Por lo tanto, una superposición constructiva solo se produce bajo un proceso conrotatorio o antarafacial. Por el contrario, para un polieno con 4 electrones n + 2, los orbitales p externos del HOMO en estado fundamental son del mismo signo. Por lo tanto, la superposición orbital constructiva ocurre con un proceso disrotatorio o suprafacial. [2]

Además, el diagrama de correlación para cualquier reacción electrocíclica de 4 n se parecerá al diagrama de la ciclización de 4 electrones del 1,3-butadieno, mientras que el diagrama de correlación de cualquier reacción electrocíclica de 4 n + 2 electrones se parecerá al diagrama de correlación de la ciclización de 6 electrones del 1,3,5-hexatrieno. [16]
Esto se resume en la siguiente tabla:
Un reordenamiento sigmatrópico general puede clasificarse como de orden [ i , j ], lo que significa que un enlace σ originalmente entre átomos denotados 1 y 1', adyacentes a uno o más sistemas π, se desplaza entre los átomos i y j . Por lo tanto, migra ( i − 1), ( j − 1) átomos lejos de su posición original.
Un análisis de simetría formal mediante diagramas de correlación no es de utilidad en el estudio de reordenamientos sigmatrópicos ya que, en general, solo hay elementos de simetría presentes en el estado de transición. Excepto en casos especiales (por ejemplo, reordenamientos [3,3]), no hay elementos de simetría que se conserven a medida que se recorre la coordenada de reacción. [16] [20] Sin embargo, las correlaciones orbitales entre los materiales de partida y los productos aún se pueden analizar, y las correlaciones de los orbitales del material de partida con los orbitales de productos de alta energía darán como resultado, como es habitual, procesos "simétricos prohibidos". Sin embargo, un enfoque basado en FMO (o el análisis de Dewar-Zimmerman) es más sencillo de aplicar.

Una de las clases más frecuentes de desplazamientos sigmatrópicos se clasifica como [1, j ], donde j es impar. Esto significa que un extremo del enlace σ migra ( j − 1) enlaces a través de un sistema π mientras que el otro extremo no migra. Es una reacción que involucra j + 1 electrones: j − 1 del sistema π y 2 del enlace σ. Usando el análisis FMO, se permiten reordenamientos [1, j ]-sigmatrópicos si el estado de transición tiene una superposición constructiva entre el grupo migratorio y el orbital p aceptor del HOMO. En reordenamientos [1, j ]-sigmatrópicos si j + 1 = 4 n , entonces se permite térmicamente supra/antara, y si j + 1 = 4 n + 2, entonces se permite térmicamente supra/supra o antara/antara. [20]
La otra clase predominante de reordenamientos sigmatrópicos son [3,3], en particular los reordenamientos de Cope y Claisen . En este caso, las interacciones constructivas deben darse entre los HOMO de los dos fragmentos de radicales alílicos en el estado de transición. El HOMO Ψ 2 del estado fundamental del fragmento alílico se muestra a continuación. Como los orbitales p terminales son de signo opuesto, esta reacción puede tener lugar en una topología supra/supra o en una topología antara/antara. [20]

Las reglas de selección para un reordenamiento [ i , j ]-sigmatrópico son las siguientes:
Esto se resume en la siguiente tabla:
Una cicloadición general [ p + q ] es una reacción de adición concertada entre dos componentes, uno con electrones π p y otro con electrones π q . Esta reacción tiene simetría permitida bajo las siguientes condiciones: [16]
Esto se resume en la siguiente tabla:
Una reacción general de transferencia de doble grupo que es sincrónica se puede representar como una interacción entre un componente con electrones p π y un componente con electrones q π como se muestra.

Entonces las reglas de selección son las mismas que para las reacciones de cicloadición generalizadas. [16] Es decir
Esto se resume en la siguiente tabla:
El caso de q = 0 corresponde a la eliminación térmica de los grupos R "transferidos". Existe evidencia de que las eliminaciones pirolíticas de dihidrógeno y etano a partir de 1,4-ciclohexadieno y 3,3,6,6-tetrametil-1,4-ciclohexadieno, respectivamente, representan ejemplos de este tipo de proceso pericíclico.
La reacción ene suele clasificarse como un tipo de proceso de transferencia de grupo, aunque no implica la transferencia de dos grupos unidos por enlaces σ. En cambio, solo se transfiere un enlace σ mientras se forma un segundo enlace σ a partir de un enlace π roto. Como es un proceso completamente suprafacial que involucra 6 electrones, la simetría permite su uso en condiciones térmicas. El símbolo de Woodward-Hoffmann para la reacción ene es [ π 2 s + π 2 s + σ 2 s ] ( ver más abajo ).
Aunque las reglas de Woodward-Hoffmann se enunciaron primero en términos de procesos electrocíclicos, con el tiempo se generalizaron a todas las reacciones pericíclicas, como deberían indicar la similitud y los patrones de las reglas de selección anteriores.

En las reglas generalizadas de Woodward-Hoffmann, todo se caracteriza en términos de topologías de enlace antarafacial y suprafacial . Los términos conrotatorio y disrotatorio son suficientes para describir el sentido relativo de la rotación de enlace en reacciones de apertura o cierre de anillo electrocíclico, como se ilustra a la derecha. Sin embargo, no son adecuados para describir las topologías de formación y ruptura de enlaces que tienen lugar en una reacción pericíclica general. Como se describe en detalle a continuación, en la formulación general de las reglas de Woodward-Hoffmann, los términos de rotación de enlace conrotatorio y disrotatorio son subsumidos por los términos de topología de enlace (o facialidad) antarafacial y suprafacial , respectivamente. Estos descriptores se pueden utilizar para caracterizar la topología de la formación y ruptura de enlaces que tiene lugar en cualquier proceso pericíclico.
Un componente es cualquier parte de una molécula o moléculas que funcionan como una unidad en una reacción pericíclica. Un componente está formado por uno o más átomos y cualquiera de los siguientes tipos de orbitales asociados:
El recuento de electrones de un componente es el número de electrones en el orbital o los orbitales del componente:
La topología de enlace de un componente puede ser suprafacial y antarafacial:

Con esta notación, a todas las reacciones pericíclicas se les puede asignar un descriptor, que consiste en una serie de símbolos σ/π/ω N s/a , conectados por signos + y encerrados entre corchetes, que describen, en orden, el tipo de orbital(es), el número de electrones y la topología de enlace involucrada para cada componente. A continuación se presentan algunos ejemplos ilustrativos:
Antarafacial y suprafacial están asociados con (conrotación o inversión) y (disrotación o retención), respectivamente. Un único descriptor puede corresponder a dos procesos pericíclicos que son químicamente distintos, que una reacción y su reverso microscópico a menudo se describen con dos descriptores diferentes, y que un único proceso puede tener más de un descriptor correcto. Se puede verificar, utilizando la regla de selección pericíclica que se presenta a continuación, que todas estas reacciones son procesos permitidos.
Utilizando esta notación, Woodward y Hoffmann establecen en su revisión de 1969 la formulación general para todas las reacciones pericíclicas de la siguiente manera:
Un cambio pericíclico del estado fundamental está permitido por simetría cuando el número total de componentes (4q+2) s y (4r) a es impar. [16]
Aquí, (4 q + 2) s y (4 r ) a se refieren a los componentes electrónicos suprafaciales (4 q + 2) y antarafaciales (4 r ), respectivamente. Además, este criterio debe interpretarse tanto como suficiente (enunciado anteriormente) como necesario (no enunciado explícitamente anteriormente, véase: si y solo si )
Alternativamente, la afirmación general puede formularse en términos del número total de electrones utilizando reglas simples de divisibilidad mediante un análisis directo de dos casos.
Primero, consideremos el caso donde el número total de electrones es 4 n + 2:
donde a , b , c y d son coeficientes que indican la cantidad de cada tipo de componente. Esta ecuación implica que uno de los términos a o b , pero no ambos, es impar, ya que si a y b son pares o impares, entonces la suma de los cuatro términos es 0 (mod 4).
El enunciado generalizado de las reglas de Woodward-Hoffmann establece que a + d es impar si se permite la reacción. Ahora bien, si a es par, esto implica que d es impar. Como b es impar en este caso, el número de componentes antarafaciales, b + d , es par. Asimismo, si a es impar, entonces d es par. Como b es par en este caso, el número de componentes antarafaciales, b + d , es nuevamente par. Por lo tanto, independientemente del supuesto inicial de paridad para a y b , el número de componentes antarafaciales es par cuando el conteo de electrones es 4 n + 2. Por el contrario, b + d es impar.
En el caso en que el número total de electrones sea 4 n , argumentos similares (omitidos aquí) llevan a la conclusión de que el número de componentes antarafaciales b + d debe ser impar en el caso permitido y par en el caso prohibido.
Finalmente, para completar el argumento y demostrar que este nuevo criterio es verdaderamente equivalente al criterio original, es necesario argumentar también las afirmaciones inversas, es decir, que el número de componentes antarafaciales b + d y el recuento de electrones (4 n + 2 o 4 n ) implica la paridad de a + d que se da por las reglas de Woodward-Hoffmann (impar para permitido, par para prohibido). Otra ronda de análisis de casos (algo tediosos) demostrará fácilmente que este es el caso. La regla de selección pericíclica establece:
Un proceso pericíclico que involucra 4n+2 o 4n electrones está permitido térmicamente si y solo si el número de componentes antarafaciales involucrados es par o impar, respectivamente.
En esta formulación, el recuento de electrones se refiere a todo el sistema de reacción, en lugar de a los componentes individuales, como se enumera en la declaración original de Woodward y Hoffmann. En la práctica, un número par o impar de componentes antarafaciales generalmente significa cero o un componente antarafacial, respectivamente, ya que los estados de transición que involucran dos o más componentes antarafaciales generalmente se ven desfavorecidos por la tensión. Como excepciones, ciertas reacciones intramoleculares pueden estar restringidas geométricamente de tal manera que imponen una trayectoria antarafacial para múltiples componentes. Además, en algunos casos, por ejemplo, la reorganización de Cope, se puede considerar que la misma geometría de estado de transición (no necesariamente tensa) contiene dos componentes π supra o dos antara, dependiendo de cómo se dibujen las conexiones entre los lóbulos orbitales. (Esta ambigüedad es una consecuencia de la convención de que la superposición de ambos lóbulos internos o ambos lóbulos externos de un componente σ puede considerarse suprafacial).
Esta formulación alternativa deja clara la equivalencia de las reglas de Woodward-Hoffmann con el análisis de Dewar-Zimmerman (ver abajo). Un número total par de inversiones de fase es equivalente a un número par de componentes antarafaciales y corresponde a la topología de Hückel, requiriendo 4 n + 2 electrones para aromaticidad, mientras que un número total impar de inversiones de fase es equivalente a un número impar de componentes antarafaciales y corresponde a la topología de Möbius, requiriendo 4 n electrones para aromaticidad. [24] Para resumir la teoría del estado de transición aromático: Las reacciones pericíclicas térmicas proceden a través de estados de transición de Hückel de (4 n + 2) electrones o de Möbius de (4 n ) electrones .
Como mnemónico, la formulación anterior puede resumirse de la siguiente manera:
Un proceso pericíclico de estado fundamental que involucra N pares de electrones y A componentes antarafaciales tiene simetría permitida si y solo si N + A es impar.
La equivalencia de las dos formulaciones también puede verse mediante un simple argumento de paridad sin apelar al análisis de casos.
Proposición. Las siguientes formulaciones de las reglas de Woodward-Hoffmann son equivalentes:
(A) Para una reacción pericíclica, si la suma del número de componentes suprafaciales 4q + 2 y componentes antarafacial 4r es impar, entonces está permitida térmicamente; de lo contrario, la reacción está prohibida térmicamente.
(B) Para una reacción pericíclica, si el número total de componentes antarafaciales de una reacción de (4n + 2) electrones es par o el número total de componentes antarafaciales de una reacción de 4n electrones es impar, entonces está térmicamente permitida; de lo contrario, la reacción está térmicamente prohibida.
Prueba de equivalencia: Indexe los componentes de unareacción pericíclica de k componentes y asigne al componente i con símbolo de Woodward-Hoffmann σ/π/ω N s/a el símbolo de conteo de electrones y paridad topológicade acuerdo con las siguientes reglas:
Tenemos una reformulación matemáticamente equivalente de (A) :
(A') Se permite térmicamente una colección de símbolos si y solo si el número de símbolos con la propiedad es impar.
Dado que el recuento total de electrones es 4 n + 2 o 4 n precisamente cuando (el número de componentes electrónicos (4 q + 2)) es impar o par, respectivamente, mientras que da el número de componentes antarafaciales, también podemos reformular (B) :
(B') Una colección de símbolos está permitida térmicamente si y solo si exactamente uno de o es impar.
Basta con demostrar que (A') y (B') son equivalentes. Exactamente uno de o es impar si y solo si es impar. Si , se cumple; por lo tanto, la omisión de símbolos con la propiedad de una colección no cambiará la paridad de . Por otro lado, cuando , tenemos , pero simplemente enumera el número de componentes con la propiedad . Por lo tanto,
.
Por lo tanto, y el número de símbolos en una colección con la propiedad tienen la misma paridad. Como las formulaciones (A') y (B') son equivalentes, también lo son (A) y (B) , como se afirma. □
Para dar un ejemplo concreto, a una reacción hipotética con el descriptor [ π 6 s + π 4 a + π 2 a ] se le asignaría la colección {(1, 0, 1), (0, 1, 2), (1, 1, 3)} en el esquema anterior. Hay dos componentes, (1, 0, 1) y (0, 1, 2), con la propiedad , por lo que la reacción no está permitida por (A') . Asimismo, y son ambos pares, por lo que (B') produce la misma conclusión (como debe ser): la reacción no está permitida.
Esta formulación para una reacción de 2 componentes es equivalente a las reglas de selección para reacciones de [ p + q ]-cicloadición que se muestran en la siguiente tabla:
Si el número total de electrones es 4 n + 2, entonces uno está en la fila inferior de la tabla. La reacción está permitida térmicamente si es suprafacial con respecto a ambos componentes o antarafacial con respecto a ambos componentes. Es decir, el número de componentes antarafacial es par (es 0 o 2). De manera similar, si el número total de electrones es 4 n , entonces uno está en la fila superior de la tabla. Esto está permitido térmicamente si es suprafacial con respecto a un componente y antarafacial con respecto al otro. Por lo tanto, el número total de componentes antarafacial siempre es impar, ya que siempre es 1.
Las siguientes son algunas clases de reacciones de estado fundamental (es decir, térmicas) comunes analizadas a la luz de las reglas generalizadas de Woodward-Hoffmann.

Una [2+2]-cicloadición es un proceso de 4 electrones que une dos componentes. Por lo tanto, según las reglas generales de WH anteriores, solo está permitida si la reacción es antarafacial con respecto a exactamente un componente. Esta es la misma conclusión a la que se llegó con los diagramas de correlación en la sección anterior.
A la derecha se muestra un ejemplo raro pero estereoquímicamente inequívoco de una cicloadición [ π 2 s + π 2 a ]-. La tensión y las propiedades estéricas del doble enlace trans permiten este proceso generalmente cinéticamente desfavorable. También se cree que el cis , trans -1,5-ciclooctadieno experimenta dimerización a través de este modo. [16] Las cetenas son una gran clase de reactivos que favorecen la cicloadición [2 + 2] con olefinas. El análisis de MO de la cicloadición de cetenas se vuelve complicado y ambiguo por la interacción simultánea pero independiente de los orbitales ortogonales de la cetena, pero puede involucrar también una interacción [ π 2 s + π 2 a ]. [25]
La reacción sincrónica de Diels-Alder de 6π-electrones es una [ π 4 s + π 2 s ]-cicloadición (es decir, suprafacial con respecto a ambos componentes), como lo ejemplifica la reacción de la derecha.

Por lo tanto, como el número total de componentes antarafaciales es 0, que es par, la reacción está permitida por simetría. [16] Esta predicción concuerda con el experimento, ya que la reacción de Diels-Alder es una reacción pericíclica bastante fácil.
Se puede considerar que una reacción de apertura de anillo electrocíclico de 4 n electrones tiene 2 componentes: el sistema π y la ruptura del enlace σ. Con respecto al sistema π, la reacción es suprafacial. Sin embargo, con un mecanismo conrotatorio, como se muestra en la figura anterior, la reacción es antarafacial con respecto al enlace σ. Por el contrario, con un mecanismo disrotatorio es suprafacial con respecto a la ruptura del enlace σ.
Según las reglas anteriores, para una reacción pericíclica de 4 n electrones de 2 componentes, debe haber un componente antarafacial. Por lo tanto, la reacción debe proceder a través de un mecanismo conrotatorio. [16] Esto concuerda con el resultado obtenido en los diagramas de correlación anteriores.
Una reacción de apertura de anillo electrocíclico 4 n + 2 es también una reacción pericíclica de 2 componentes que es suprafacial con respecto al sistema π. Por lo tanto, para que se permita la reacción, el número de componentes antarafaciales debe ser 0, es decir, debe ser suprafacial con respecto al enlace σ de ruptura también. Por lo tanto, se permite un mecanismo disrotatorio por simetría. [16]

Un reordenamiento sigmatrópico [1, j ] también es una reacción pericíclica de dos componentes: un componente es el sistema π, el otro componente es el grupo migratorio. El caso más simple es un desplazamiento de hidruro [1, j ] a través de un sistema π donde j es impar. En este caso, como el hidrógeno solo tiene un orbital s esféricamente simétrico, la reacción debe ser suprafacial con respecto al hidrógeno. El número total de electrones involucrados es ( j + 1) ya que hay ( j − 1)/2 enlaces π más el enlace σ involucrado en la reacción. Si j = 4 n − 1, entonces debe ser antarafacial, y si j = 4 n + 1, entonces debe ser suprafacial. [16] Esto concuerda con el experimento de que los cambios de [1,3]-hidruro generalmente no se observan ya que el proceso antarafacial permitido por la simetría no es factible, pero los cambios de [1,5]-hidruro son bastante fáciles.
Para un desplazamiento de [1, j ]-alquilo, donde la reacción puede ser antarafacial (es decir, estereoquímica invertida) con respecto al centro de carbono, se aplican las mismas reglas. Si j = 4 n − 1, entonces la reacción es simétricamente permitida si es antarafacial con respecto al sistema π o invierte la estereoquímica en el carbono. Si j = 4 n + 1, entonces la reacción es simétricamente permitida si es suprafacial con respecto al sistema π y conserva la estereoquímica en el centro de carbono. [16]
A la derecha se encuentra uno de los primeros ejemplos de un desplazamiento [1,3]-sigmatrópico descubierto, informado por Berson en 1967. [26] Para permitir la inversión de la configuración, a medida que se rompe el enlace σ, la fracción C(H)(D) gira en el estado de transición, con la hibridación del carbono aproximándose a sp 2 , de modo que el orbital p no hibridado restante mantiene la superposición con ambos carbonos 1 y 3.

Las reglas generalizadas de Woodward-Hoffmann, dadas por primera vez en 1969, son equivalentes a un enfoque general anterior, el concepto de Möbius-Hückel de Zimmerman, que se enunció por primera vez en 1966 y también se conoce como teoría del estado de transición aromático . [3] [27] [28] Como principio central, la teoría del estado de transición aromático sostiene que las reacciones pericíclicas "permitidas" proceden a través de estados de transición con carácter aromático, mientras que las reacciones pericíclicas "prohibidas" encontrarían estados de transición que son de naturaleza antiaromática. En el análisis de Dewar-Zimmerman, uno se preocupa por la topología del estado de transición de la reacción pericíclica. Si el estado de transición involucra 4 n electrones, la topología de Möbius es aromática y la topología de Hückel es antiaromática, mientras que si el estado de transición involucra 4 n + 2 electrones, la topología de Hückel es aromática y la topología de Möbius es antiaromática. La paridad del número de inversiones de fase (descritas en detalle a continuación) en el estado de transición determina su topología. Una topología de Möbius implica un número impar de inversiones de fase, mientras que una topología de Hückel implica un número par de inversiones de fase.

En relación con la terminología de Woodward-Hoffmann, el número de componentes antarafaciales y el número de inversiones de fase siempre tienen la misma paridad. [24] En consecuencia, un número impar de componentes antarafaciales da la topología de Möbius, mientras que un número par da la topología de Hückel. Por lo tanto, para reformular los resultados de la teoría del estado de transición aromático en el lenguaje de Woodward y Hoffmann, una reacción de 4 n -electrones está permitida térmicamente si y solo si tiene un número impar de componentes antarafaciales (es decir, topología de Möbius); una reacción de (4 n + 2)-electrones está permitida térmicamente si y solo si tiene un número par de componentes antarafaciales (es decir, topología de Hückel).
Procedimiento para el análisis de Dewar-Zimmerman (ejemplos mostrados a la derecha): Paso 1. Sombrear todos los orbitales base que son parte del sistema pericíclico. El sombreado puede ser arbitrario. En particular, el sombreado no necesita reflejar la fase de los OM de polieno; cada orbital base simplemente necesita tener dos lóbulos de fase opuesta en el caso de orbitales híbridos p o sp x , o una sola fase en el caso de un orbital s. Paso 2. Dibujar conexiones entre los lóbulos de los orbitales base que están geométricamente bien dispuestos para interactuar en el estado de transición. Las conexiones a realizar dependen de la topología del estado de transición. (Por ejemplo, en la figura, se muestran diferentes conexiones en los casos de electrociclación con- y disrotatoria). Paso 3. Cuente el número de conexiones que ocurren entre lóbulos de sombreado opuesto: cada una de estas conexiones constituye una inversión de fase. Si el número de inversiones de fase es par, el estado de transición es Hückel, mientras que si el número de inversiones de fase es impar, el estado de transición es Möbius. Paso 4. Concluya que la reacción pericíclica está permitida si el conteo de electrones es 4 n + 2 y el estado de transición es Hückel, o si el conteo de electrones es 4 n y el estado de transición es Möbius; de lo contrario, concluya que la reacción pericíclica está prohibida.
Es importante destacar que cualquier esquema de asignación de fases relativas a los orbitales base es aceptable, ya que invertir la fase de cualquier orbital individual agrega 0 o ±2 inversiones de fase al total, un número par, de modo que la paridad del número de inversiones (número de inversiones módulo 2) no cambia.
Recientemente, las reglas de Woodward-Hoffmann han sido reinterpretadas utilizando la teoría funcional de la densidad (DFT) conceptual. [29] [30] La clave para el análisis es la función de descriptor dual, propuesta por Christophe Morell, André Grand y Alejandro Toro-Labbé [31] , la segunda derivada de la densidad electrónica con respecto al número de electrones . Esta función de respuesta es importante ya que la reacción de dos componentes A y B que implica una transferencia de electrones dependerá de la capacidad de respuesta de la densidad electrónica a la donación o aceptación de electrones, es decir, la derivada de la función de Fukui . De hecho, desde un punto de vista simplista, la función de descriptor dual da una lectura de la electrofilicidad o nucleofilicidad de las diversas regiones de la molécula. Para , la región es electrofílica, y para , la región es nucleófila. Utilizando el supuesto de orbital molecular de frontera y una aproximación de diferencia finita de la función de Fukui, se puede escribir el descriptor dual como
Esto tiene sentido intuitivo, ya que si una región es mejor para aceptar electrones que para donarlos, entonces el término LUMO debe dominar y la función de descriptor dual será positiva. Por el contrario, si una región es mejor para donar electrones, entonces el término HOMO dominará y el descriptor será negativo. Observe que, aunque el concepto de fase y orbitales se reemplaza simplemente por la noción de densidad electrónica, esta función aún toma valores positivos y negativos.

Las reglas de Woodward-Hoffmann se reinterpretan utilizando esta formulación haciendo coincidir las interacciones favorables entre regiones de densidad electrónica para las que el descriptor dual tiene signos opuestos. Esto es equivalente a maximizar las interacciones favorables predichas y minimizar las interacciones repulsivas. Para el caso de una cicloadición [4+2], se muestra un esquema simplificado de los reactivos con la función del descriptor dual coloreada (rojo = positivo, azul = negativo) en la configuración supra/supra óptima a la izquierda. Este método predice correctamente las reglas WH para las principales clases de reacciones pericíclicas.
En el capítulo 12 de La conservación de la simetría orbital , titulado "Violaciones", Woodward y Hoffmann afirmaron:
¡No hay ninguna! Tampoco se puede esperar que se viole un principio tan fundamental de máxima vinculación.
A pesar de este pronunciamiento, es importante reconocer que las reglas de Woodward-Hoffmann se utilizan para predecir alturas de barrera relativas y, por lo tanto, mecanismos de reacción probables, y que solo tienen en cuenta las barreras debidas a la conservación de la simetría orbital. Por lo tanto, no se garantiza que una reacción permitida por la simetría WH realmente tenga lugar de manera fácil. Por el contrario, es posible, con suficiente entrada de energía, lograr un producto anti-Woodward-Hoffmann. Esto es especialmente frecuente en sistemas estéricamente restringidos, donde el producto WH tiene una barrera estérica adicional que superar. Por ejemplo, en la apertura de anillo electrocíclica del derivado de dimetilbiciclo[0.2.3]hepteno ( 1 ), no es posible un mecanismo conrotatorio debido a la tensión angular resultante y la reacción avanza lentamente a través de un mecanismo disrotatorio a 400 o C para dar un producto de cicloheptadieno. [2] También se pueden observar violaciones en casos con fuerzas impulsoras termodinámicas muy fuertes. La descomposición de la dioxetano-1,2-diona en dos moléculas de dióxido de carbono, famosa por su papel en la luminiscencia de las barras luminosas , ha sido estudiada computacionalmente. En ausencia de fluorescentes, ahora se cree que la reacción se desarrolla de manera concertada (aunque asincrónica), a través de una retro-[2+2]-cicloadición que viola formalmente las reglas de Woodward-Hoffmann. [32]


De manera similar, un artículo reciente describe cómo se puede utilizar el estrés mecánico para remodelar las vías de reacción química y obtener productos que aparentemente violan las reglas de Woodward-Hoffman. [33] En este artículo, utilizan la irradiación ultrasónica para inducir un estrés mecánico en polímeros funcionalizados con enlaces unidos syn o anti en el anillo de ciclobuteno. Los estudios computacionales predicen que la fuerza mecánica, resultante de la fricción de los polímeros, induce el alargamiento del enlace a lo largo de la coordenada de reacción del mecanismo conrotatorio en el ciclobuteno anti-bisustituido, y a lo largo de la coordenada de reacción del mecanismo disrotatorio en el ciclobuteno syn-bisustituido. Por lo tanto, en el ciclobuteno syn-bisustituido, se predice que se formará el producto anti -WH.
Esta predicción computacional fue respaldada por un experimento en el sistema que se muestra a continuación. Los polímeros funcionalizados con enlaces se conjugaron con cis benzociclobuteno en conformaciones syn y anti. Como se predijo, ambos productos dieron el mismo producto (Z,Z), según se determinó mediante la extinción mediante una reacción estereoespecífica de Diels-Alder con la maleimida sustituida. En particular, el producto sustituido con syn dio el producto anti-WH, presumiblemente porque el estiramiento mecánico a lo largo de la coordenada de la vía disrotatoria redujo la barrera de la reacción bajo la vía disrotatoria lo suficiente como para sesgar ese mecanismo.

Se ha afirmado que Elias James Corey , también ganador del Premio Nobel, se siente responsable de las ideas que sentaron las bases de esta investigación, y que Woodward injustamente olvidó darle crédito por el descubrimiento. En una memoria de 2004 publicada en el Journal of Organic Chemistry , [34] Corey hace su afirmación de la prioridad de la idea: "El 4 de mayo de 1964, sugerí a mi colega RB Woodward una explicación simple que involucraba la simetría de los orbitales moleculares perturbados (HOMO) para las conversiones estereoselectivas de ciclobuteno a 1,3-butadieno y 1,3,5-hexatrieno a ciclohexadieno que proporcionaron la base para el desarrollo posterior de estas ideas en lo que se conoció como las reglas de Woodward-Hoffmann".
Corey, que entonces tenía 35 años, estaba trabajando hasta la tarde del lunes 4 de mayo, como solían hacer él y otros químicos motivados. Alrededor de las 8:30 p. m., pasó por la oficina de Woodward, y Woodward le planteó una pregunta sobre cómo predecir el tipo de anillo que formaría una cadena de átomos. Después de un breve debate, Corey propuso que la configuración de los electrones gobernaba el curso de la reacción. Woodward insistió en que la solución no funcionaría, pero Corey dejó dibujos en la oficina, seguro de que estaba en lo cierto. [35]
"Pensé que esto iba a ser un desarrollo realmente interesante y estaba deseando que se llevara a cabo algún tipo de proyecto conjunto", escribió. Pero al día siguiente, Woodward voló a la oficina de Corey cuando él y un colega salían a almorzar y presentó la idea de Corey como si fuera suya... y luego se fue. Corey estaba atónito.
En una refutación de 2004 publicada en Angewandte Chemie , [36] Roald Hoffmann negó la afirmación: cita a Woodward de una conferencia dada en 1966 diciendo: "RECUERDO muy claramente -y todavía me sorprende un poco- que el destello crucial de iluminación me llegó en forma algebraica, en lugar de en forma pictórica o geométrica. De repente, se me ocurrió que los coeficientes de los términos terminales en la expresión matemática que representa el orbital molecular ocupado más alto del butadieno eran de signo opuesto, mientras que los de la expresión correspondiente para el hexatrieno poseían el mismo signo. Desde aquí sólo había un pequeño paso hasta la visión geométrica, y más obviamente químicamente relevante, de que en la ciclización interna de un dieno, la cara superior de un átomo terminal debería atacar la cara inferior del otro, mientras que en el caso del trieno, la formación de un nuevo enlace debería involucrar las caras superiores (o pari passu, las inferiores) de ambos átomos terminales".
Además, Hoffmann señala que en dos publicaciones de 1963 [37] y 1965 [38] , Corey describió una síntesis total del compuesto dihidrocostunolida. Aunque describen una reacción electrocíclica, Corey no tiene nada que ofrecer con respecto a la explicación de la estereoespecificidad de la síntesis.
Esta reacción fotoquímica que involucra 6 = 4×1 + 2 electrones ahora se reconoce como conrotatoria.