Pandeo

Cambio repentino en la forma de un componente estructural bajo carga

Paneles de revestimiento abombados en un avión B-52 . Los paneles de revestimiento finos se abomban con cargas muy bajas. En el caso que se muestra aquí, el peso de la estructura delantera del fuselaje, delante del tren de aterrizaje delantero, es suficiente para hacer que los paneles se abomben. Los paneles abombados siguen siendo eficaces para soportar la fuerza cortante mediante tensión diagonal. ^[1]

En ingeniería estructural , el pandeo es el cambio repentino de forma ( deformación ) de un componente estructural bajo carga , como la curvatura de una columna bajo compresión o la arruga de una placa bajo esfuerzo cortante . Si una estructura está sujeta a una carga que aumenta gradualmente, cuando la carga alcanza un nivel crítico, un miembro puede cambiar repentinamente de forma y se dice que la estructura y el componente se han pandeado . ^[2] La carga crítica de Euler y la fórmula parabólica de Johnson se utilizan para determinar la tensión de pandeo de una columna.

El pandeo puede producirse incluso aunque las tensiones que se desarrollan en la estructura sean muy inferiores a las necesarias para provocar un fallo en el material del que está compuesta. Una carga adicional puede provocar deformaciones significativas y algo impredecibles, que posiblemente lleven a la pérdida total de la capacidad de carga del elemento. Sin embargo, si las deformaciones que se producen después del pandeo no provocan el colapso completo de ese elemento, este seguirá soportando la carga que provocó su pandeo. Si el elemento pandeado forma parte de un conjunto más grande de componentes, como un edificio, cualquier carga aplicada a la parte pandeada de la estructura que supere la que provocó el pandeo del elemento se redistribuirá dentro de la estructura. Algunas aeronaves están diseñadas para que los paneles de revestimiento delgados sigan soportando la carga incluso en estado pandeado.

Formas de pandeo

Columnas

Una columna bajo una carga axial concéntrica que presenta la deformación característica de pandeo.

La excentricidad de la fuerza axial genera un momento de flexión que actúa sobre el elemento de viga.

La relación entre la longitud efectiva de una columna y el radio de giro mínimo de su sección transversal se denomina relación de esbeltez (a veces expresada con la letra griega lambda, λ). Esta relación permite clasificar las columnas y su modo de falla. La relación de esbeltez es importante para las consideraciones de diseño. Todos los siguientes son valores aproximados que se utilizan para mayor comodidad.

Si la carga sobre una columna se aplica a través del centro de gravedad (centroide) de su sección transversal, se denomina carga axial . Una carga en cualquier otro punto de la sección transversal se conoce como carga excéntrica. Una columna corta bajo la acción de una carga axial fallará por compresión directa antes de pandearse, pero una columna larga cargada de la misma manera fallará saltando repentinamente hacia afuera lateralmente (pandeo) en un modo de flexión. El modo de pandeo de deflexión se considera un modo de falla y generalmente ocurre antes de que las tensiones de compresión axial (compresión directa) puedan causar la falla del material por fluencia o fractura de ese miembro comprimido. Sin embargo, las columnas de longitud intermedia fallarán por una combinación de tensión de compresión directa y flexión.

En particular:

• Una columna de acero corta es aquella cuya relación de esbeltez no excede de 50; una columna de acero de longitud intermedia tiene una relación de esbeltez que varía entre aproximadamente 50 y 200, y su comportamiento está dominado por el límite de resistencia del material, mientras que se puede suponer que una columna de acero larga tiene una relación de esbeltez mayor de 200 y su comportamiento está dominado por el módulo de elasticidad del material.
• Una columna de hormigón corta es aquella que tiene una relación entre la longitud sin soporte y la dimensión mínima de la sección transversal igual o menor a 10. Si la relación es mayor a 10, se considera una columna larga (a veces denominada columna esbelta).
• Las columnas de madera pueden clasificarse como columnas cortas si la relación entre la longitud y la dimensión mínima de la sección transversal es igual o menor que 10. La línea divisoria entre columnas de madera intermedias y largas no se puede evaluar fácilmente. Una forma de definir el límite inferior de las columnas de madera largas sería establecerlo como el valor más pequeño de la relación entre la longitud y la sección transversal mínima que exceda una cierta constante K del material. Dado que K depende del módulo de elasticidad y de la tensión de compresión admisible paralela a la fibra, se puede ver que este límite arbitrario variaría con la especie de madera. El valor de K se proporciona en la mayoría de los manuales de estructura.

La teoría del comportamiento de las columnas fue investigada en 1757 por el matemático Leonhard Euler . Derivó la fórmula, denominada carga crítica de Euler , que proporciona la carga axial máxima que una columna ideal, larga y esbelta, puede soportar sin pandearse. Una columna ideal es aquella que:

• perfectamente recto
• Hecho de un material homogéneo
• libre del estrés inicial.

Cuando la carga aplicada alcanza la carga de Euler, a veces llamada carga crítica, la columna pasa a un estado de equilibrio inestable . Con esa carga, la introducción de la más mínima fuerza lateral hará que la columna falle al "saltar" repentinamente a una nueva configuración, y se dice que la columna se ha pandeado. Esto es lo que sucede cuando una persona se para sobre una lata de aluminio vacía y luego golpea brevemente los lados, lo que hace que se aplaste instantáneamente (los lados verticales de la lata pueden entenderse como una serie infinita de columnas extremadamente delgadas). ^{[ cita requerida ]} La fórmula derivada por Euler para columnas largas y delgadas es

$${\displaystyle F_{c}={\frac {\pi ^{2}EI}{(KL)^{2}}}}$$

dónde

• ${\displaystyle F_{c}}$, fuerza máxima o crítica (carga vertical sobre la columna),
• ${\displaystyle E}$, módulo de elasticidad ,
• ${\displaystyle I}$, momento de inercia del área más pequeña (segundo momento de área) de la sección transversal de la columna,
• ${\displaystyle L}$, longitud de columna sin soporte,
• ${\displaystyle K}$, factor de longitud efectiva de la columna , cuyo valor depende de las condiciones de apoyo del extremo de la columna, como se indica a continuación.
  • Para ambos extremos fijados con pasadores (bisagrasables, libres para girar) . ${\displaystyle K=1.0}$
  • Para ambos extremos fijos, . ${\displaystyle K=0.50}$
  • Para un extremo fijo y el otro extremo fijado con pasador, . ${\displaystyle K\approx 0.699}$
  • Para un extremo fijo y el otro extremo libre para moverse lateralmente, . ${\displaystyle K=2.0}$
• ${\displaystyle KL}$es la longitud efectiva de la columna.

El examen de esta fórmula revela los siguientes hechos con respecto a la capacidad de carga de columnas esbeltas.

• La elasticidad del material de la columna y no la resistencia a la compresión del material de la columna determina la carga de pandeo de la columna.
• La carga de pandeo es directamente proporcional al segundo momento del área de la sección transversal.
• Las condiciones de contorno tienen un efecto considerable en la carga crítica de columnas esbeltas. Las condiciones de contorno determinan el modo de flexión de la columna y la distancia entre los puntos de inflexión en la curva de desplazamiento de la columna desviada. Los puntos de inflexión en la forma de deflexión de la columna son los puntos en los que la curvatura de la columna cambia de signo y también son los puntos en los que los momentos de flexión internos de la columna son cero. Cuanto más cercanos estén los puntos de inflexión, mayor será la capacidad de carga axial resultante (carga de pandeo) de la columna.

Modelo de demostración que ilustra los diferentes modos de pandeo de Euler. El modelo muestra cómo las condiciones de contorno afectan la carga crítica de una columna esbelta. Las columnas son idénticas, salvo por las condiciones de contorno.

De lo anterior se deduce que la carga de pandeo de una columna se puede aumentar cambiando su material por uno con un módulo de elasticidad (E) más alto, o modificando el diseño de la sección transversal de la columna para aumentar su momento de inercia. Esto último se puede hacer sin aumentar el peso de la columna distribuyendo el material lo más lejos posible del eje principal de la sección transversal de la columna. Para la mayoría de los propósitos, el uso más eficaz del material de una columna es el de una sección tubular.

Otra idea que se puede extraer de esta ecuación es el efecto de la longitud sobre la carga crítica. Si se duplica la longitud no soportada de la columna, se reduce a cuatro la carga admisible. La restricción que ofrecen las conexiones de los extremos de una columna también afecta a su carga crítica. Si las conexiones son perfectamente rígidas (no permiten la rotación de sus extremos), la carga crítica será cuatro veces mayor que la de una columna similar en la que los extremos están articulados (lo que permite la rotación de sus extremos).

Dado que el radio de giro se define como la raíz cuadrada de la relación entre el momento de inercia de la columna alrededor de un eje y su área de sección transversal, la fórmula de Euler anterior se puede reformatear sustituyendo el radio de giro por : ${\displaystyle Ar^{2}}$ ${\displaystyle I}$

$${\displaystyle \sigma ={\frac {F}{A}}={\frac {\pi ^{2}E}{(l/r)^{2}}}}$$

donde es la tensión que provoca el pandeo en la columna, y es la relación de esbeltez. ${\displaystyle \sigma =F/A}$ ${\displaystyle l/r}$

Dado que las columnas estructurales suelen tener una longitud intermedia, la fórmula de Euler tiene poca aplicación práctica en el diseño ordinario. Entre los problemas que provocan desviaciones del comportamiento puro de la columna de Euler se incluyen imperfecciones en la geometría de la columna en combinación con el comportamiento de plasticidad/tensión-deformación no lineal del material de la columna. En consecuencia, se han desarrollado varias fórmulas empíricas para columnas que coinciden con los datos de prueba, todas las cuales incorporan la relación de esbeltez. Debido a la incertidumbre en el comportamiento de las columnas, para el diseño, se introducen factores de seguridad adecuados en estas fórmulas. Una de estas fórmulas es la fórmula de Perry Robertson , que estima la carga crítica de pandeo basándose en una pequeña curvatura inicial supuesta, por lo tanto, una excentricidad de la carga axial. La fórmula de Rankine Gordon, llamada así por William John Macquorn Rankine y Perry Hugesworth Gordon (1899 – 1966), también se basa en resultados experimentales y sugiere que una columna se pandeará con una carga Fmax _dada por: $${\displaystyle {\frac {1}{F_{\max }}}={\frac {1}{F_{e}}}+{\frac {1}{F_{c}}}}$$

donde es la carga máxima de Euler y es la carga de compresión máxima. Esta fórmula generalmente produce una estimación conservadora de . ${\displaystyle F_{e}}$ ${\displaystyle F_{c}}$ ${\displaystyle F_{\max }}$

Autopandeo

Una columna vertical independiente, con densidad , módulo de Young y área de sección transversal , se doblará bajo su propio peso si su altura excede un cierto valor crítico: ^{[3] [4] [5]} ${\displaystyle \rho }$ ${\displaystyle E}$ ${\displaystyle A}$

$${\displaystyle h_{\text{crit}}=\left({\frac {9B^{2}}{4}}\,{\frac {EI}{\rho gA}}\right)^{\frac {1}{3}}}$$

donde es la aceleración debida a la gravedad, es el segundo momento del área de la sección transversal de la viga, y es el primer cero de la función de Bessel de primera clase de orden −1/3, que es igual a 1,86635086... ${\displaystyle g}$ ${\displaystyle I}$ ${\displaystyle B}$

Pandeo de placa

Una placa es una estructura tridimensional que se define por tener un ancho comparable a su longitud, con un espesor muy pequeño en comparación con sus otras dos dimensiones. De manera similar a las columnas, las placas delgadas experimentan deformaciones por pandeo fuera del plano cuando se someten a cargas críticas; sin embargo, a diferencia del pandeo de las columnas, las placas bajo cargas de pandeo pueden seguir soportando cargas, lo que se denomina pandeo local. Este fenómeno es increíblemente útil en numerosos sistemas, ya que permite diseñar sistemas para proporcionar mayores capacidades de carga.

Para una placa rectangular, apoyada a lo largo de cada borde, cargada con una fuerza de compresión uniforme por unidad de longitud, la ecuación de gobierno derivada puede enunciarse como: ^[6]

$${\displaystyle {\frac {\partial ^{4}w}{\partial x^{4}}}+2{\frac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\frac {\partial ^{4}w}{\partial y^{4}}}={\frac {12\left(1-\nu ^{2}\right)}{Et^{3}}}\left(-N_{x}{\frac {\partial ^{2}w}{\partial x^{2}}}\right)}$$

dónde

• ${\displaystyle w}$, desviación fuera del plano
• ${\displaystyle N_{x}}$, carga de compresión distribuida uniformemente
• ${\displaystyle \nu }$, coeficiente de Poisson
• ${\displaystyle E}$, módulo de elasticidad
• ${\displaystyle t}$, espesor

La solución de la desviación se puede ampliar en dos funciones armónicas que se muestran: ^[6]

$${\displaystyle w=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }w_{mn}\sin \left({\frac {m\pi x}{a}}\right)\sin \left({\frac {n\pi y}{b}}\right)}$$

dónde

• ${\displaystyle m}$, número de curvaturas de medio seno que ocurren longitudinalmente
• ${\displaystyle n}$, número de curvaturas de medio seno que ocurren a lo ancho
• ${\displaystyle a}$, longitud de la muestra
• ${\displaystyle b}$, ancho de la muestra

La ecuación anterior se puede sustituir en la ecuación diferencial anterior donde es igual a 1. se puede separar proporcionando la ecuación para la carga de compresión crítica de una placa: ^[6] ${\displaystyle n}$ ${\displaystyle N_{x}}$

$${\displaystyle N_{x,cr}=k_{cr}{\frac {\pi ^{2}Et^{3}}{12\left(1-\nu ^{2}\right)b^{2}}}}$$

donde el coeficiente de pandeo , viene dado por: ^[6] ${\displaystyle k_{cr}}$ $${\displaystyle k_{cr}=\left({\frac {mb}{a}}+{\frac {a}{mb}}\right)^{2}}$$

El coeficiente de pandeo está influenciado por el aspecto de la muestra, / , y el número de curvaturas longitudinales. Para un número creciente de tales curvaturas, la relación de aspecto produce un coeficiente de pandeo variable; pero cada relación proporciona un valor mínimo para cada . Este valor mínimo puede entonces usarse como una constante, independiente tanto de la relación de aspecto como de . ^[6] ${\displaystyle a}$ ${\displaystyle {b}}$ ${\displaystyle m}$ ${\displaystyle m}$

Dado que la tensión se encuentra por la carga por unidad de área, se encuentra la siguiente expresión para la tensión crítica: $${\displaystyle \sigma _{cr}=k_{cr}{\frac {\pi ^{2}E}{12\left(1-\nu ^{2}\right)\left({\frac {b}{t}}\right)^{2}}}}$$

A partir de las ecuaciones derivadas, se puede ver las estrechas similitudes entre la tensión crítica para una columna y para una placa. A medida que el ancho se contrae, la placa actúa más como una columna ya que aumenta la resistencia al pandeo a lo largo del ancho de la placa. El aumento de permite un aumento del número de ondas sinusoidales producidas por el pandeo a lo largo, pero también aumenta la resistencia del pandeo a lo largo del ancho. ^[6] Esto crea la preferencia de la placa a pandearse de tal manera que iguale el número de curvaturas tanto a lo largo como a lo ancho. Debido a las condiciones de contorno, cuando una placa se carga con una tensión crítica y se pandea, los bordes perpendiculares a la carga no pueden deformarse fuera del plano y, por lo tanto, continuarán soportando las tensiones. Esto crea una carga de compresión no uniforme a lo largo de los extremos, donde las tensiones se imponen en la mitad del ancho efectivo a cada lado de la muestra, dada por lo siguiente: ^[6] ${\displaystyle b}$ ${\displaystyle a}$

$${\displaystyle {\frac {b_{\text{eff}}}{b}}\approx {\sqrt {{\frac {\sigma _{cr}}{\sigma _{y}}}\left(1-1.022{\sqrt {\frac {\sigma _{cr}}{\sigma _{y}}}}\right)}}}$$

dónde

• ${\displaystyle b_{\text{eff}}}$, ancho efectivo
• ${\displaystyle \sigma _{y}}$, tensión de fluencia

A medida que aumenta la tensión de carga, el ancho efectivo continúa reduciéndose; si las tensiones en los extremos alguna vez alcanzan la tensión de fluencia, la placa fallará. Esto es lo que permite que la estructura pandeada continúe soportando cargas. Cuando se grafica la carga axial sobre la carga crítica contra el desplazamiento, se muestra la trayectoria fundamental. Demuestra la similitud de la placa con una columna bajo pandeo; sin embargo, más allá de la carga de pandeo, la trayectoria fundamental se bifurca en una trayectoria secundaria que se curva hacia arriba, lo que proporciona la capacidad de estar sujeta a cargas más altas más allá de la carga crítica.

Pandeo por flexión-torsional

El pandeo por flexión y torsión se puede describir como una combinación de la respuesta de flexión y torsión de un elemento en compresión. Este modo de deflexión debe tenerse en cuenta para fines de diseño. Esto ocurre principalmente en columnas con secciones transversales "abiertas" y, por lo tanto, tienen una baja rigidez torsional, como canales, tes estructurales, formas de ángulos dobles y ángulos simples de lados iguales. Las secciones transversales circulares no experimentan este modo de pandeo.

Pandeo lateral-torsional

Pandeo lateral-torsional de una viga I con fuerza vertical en el centro: a) vista longitudinal, b) sección transversal cerca del apoyo, c) sección transversal en el centro con pandeo lateral-torsional

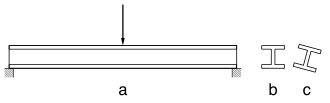
Cuando una viga simplemente apoyada se carga en flexión , el lado superior está en compresión y el lado inferior está en tensión . Si la viga no está apoyada en la dirección lateral (es decir, perpendicular al plano de flexión), y la carga de flexión aumenta hasta un límite crítico, la viga experimentará una deflexión lateral del ala de compresión a medida que se pandea localmente. La deflexión lateral del ala de compresión está restringida por el alma de la viga y el ala de tensión, pero para una sección abierta el modo de torsión es más flexible, por lo tanto, la viga se tuerce y se desvía lateralmente en un modo de falla conocido como pandeo lateral-torsional . En secciones de ala ancha (con alta rigidez de flexión lateral), el modo de deflexión será principalmente torsión en torsión. En secciones de ala estrecha, la rigidez de flexión es menor y la deflexión de la columna será más cercana a la del modo de deflexión de pandeo lateral.

El uso de secciones cerradas, como secciones huecas cuadradas, mitigará los efectos del pandeo lateral-torsional en virtud de su alta rigidez torsional .

C _b es un factor de modificación utilizado en la ecuación para la resistencia nominal a la flexión cuando se determina el pandeo lateral por torsión. La razón de este factor es permitir diagramas de momento no uniformes cuando los extremos de un segmento de viga están arriostrados. El valor conservador para C _b puede tomarse como 1, independientemente de la configuración de la viga o la carga, pero en algunos casos puede ser excesivamente conservador. C _b es siempre igual o mayor que 1, nunca menor. Para voladizos o voladizos donde el extremo libre no está arriostrado, C _b es igual a 1. Existen tablas de valores de C _b para vigas simplemente apoyadas.

Si en las tablas no se proporciona un valor apropiado de C _b , se puede obtener mediante la siguiente fórmula:

$${\displaystyle C_{b}={\frac {12.5M_{\max }}{2.5M_{\max }+3M_{A}+4M_{B}+3M_{C}}}}$$

dónde

• ${\displaystyle M_{\max }}$, valor absoluto del momento máximo en el segmento no arriostrado,
• ${\displaystyle M_{A}}$, valor absoluto del momento máximo en el punto cuarto del segmento no arriostrado,
• ${\displaystyle M_{B}}$, valor absoluto del momento máximo en la línea central del segmento no arriostrado,
• ${\displaystyle M_{C}}$, valor absoluto del momento máximo en el punto tres cuartos del segmento no arriostrado,

El resultado es el mismo para todos los sistemas de unidades.

Pandeo de plástico

La resistencia al pandeo de un elemento es menor que la resistencia al pandeo elástico de una estructura si el material del elemento se somete a una tensión que va más allá del rango de material elástico y dentro del rango de comportamiento de material no lineal (plástico). Cuando la carga de compresión está cerca de la carga de pandeo, la estructura se doblará significativamente y el material de la columna divergirá de un comportamiento de tensión-deformación lineal. El comportamiento de tensión-deformación de los materiales no es estrictamente lineal incluso por debajo del punto de fluencia, por lo que el módulo de elasticidad disminuye a medida que aumenta la tensión, y de manera significativa a medida que las tensiones se acercan a la resistencia al fluencia del material. Esta rigidez reducida del material reduce la resistencia al pandeo de la estructura y da como resultado una carga de pandeo menor que la predicha por el supuesto de un comportamiento elástico lineal.

Se puede obtener una aproximación más precisa de la carga de pandeo mediante el uso del módulo de elasticidad tangente, E _t , que es menor que el módulo elástico, en lugar del módulo elástico de elasticidad. La tangente es igual al módulo elástico y luego disminuye más allá del límite proporcional. El módulo tangente es una línea trazada tangente a la curva de tensión-deformación en un valor particular de deformación (en la sección elástica de la curva de tensión-deformación, el módulo tangente es igual al módulo elástico). Los gráficos del módulo de elasticidad tangente para una variedad de materiales están disponibles en referencias estándar.

Herida

Las secciones que están formadas por placas con bridas, como un canal, aún pueden soportar carga en las esquinas después de que las bridas se hayan pandeado localmente. La deformación es la falla de la sección completa. ^[1]

Tensión diagonal

Debido a que las capas delgadas que se utilizan normalmente en las aplicaciones aeroespaciales pueden pandearse con niveles bajos de carga, una vez pandeadas, en lugar de poder transmitir fuerzas de corte, aún pueden soportar carga a través de tensiones de tensión diagonal (DT) en el alma. Esto da como resultado un comportamiento no lineal en el comportamiento de carga de estos detalles. La relación entre la carga real y la carga a la que se produce el pandeo se conoce como la relación de pandeo de una lámina. ^[1] Las relaciones de pandeo altas pueden provocar un arrugamiento excesivo de las láminas, que luego pueden fallar debido a la fluencia de las arrugas. Aunque pueden pandearse, las láminas delgadas están diseñadas para no deformarse permanentemente y volver a un estado desenrollado cuando se elimina la carga aplicada. El pandeo repetido puede provocar fallas por fatiga .

Las láminas bajo tensión diagonal están sostenidas por refuerzos que, como resultado del pandeo de las láminas, soportan una carga distribuida a lo largo de su longitud y, a su vez, pueden provocar que estos elementos estructurales fallen por pandeo.

Las placas más gruesas pueden formar solo parcialmente un campo de tensión diagonal y pueden continuar soportando parte de la carga mediante esfuerzo cortante. Esto se conoce como tensión diagonal incompleta (IDT). Wagner estudió este comportamiento y estas vigas a veces se conocen como vigas Wagner. ^[1]

La tensión diagonal también puede generar una fuerza de tracción sobre los elementos de fijación, como los remaches, que se utilizan para fijar la estructura a los elementos de soporte. Los elementos de fijación y las láminas deben estar diseñados para resistir que se los desprenda de sus soportes.

Pandeo dinámico

Si una columna se carga de repente y luego se libera la carga, la columna puede soportar una carga mucho mayor que su carga de pandeo estática (aplicada lentamente). Esto puede suceder en una columna larga y sin soporte que se utiliza como un martillo de caída. La duración de la compresión en el extremo de impacto es el tiempo necesario para que una onda de tensión se desplace a lo largo de la columna hasta el otro extremo (libre) y vuelva a bajar como una onda de alivio. El pandeo máximo se produce cerca del extremo de impacto a una longitud de onda mucho más corta que la longitud de la varilla y a una tensión muchas veces superior a la tensión de pandeo de una columna cargada estáticamente. La condición crítica para que la amplitud de pandeo permanezca inferior a aproximadamente 25 veces la imperfección de rectitud efectiva de la varilla en la longitud de onda de pandeo es

$${\displaystyle \sigma L=\rho c^{2}h}$$

donde es la tensión de impacto, es la longitud de la varilla, es la velocidad de onda elástica y es la dimensión lateral más pequeña de una varilla rectangular. Debido a que la longitud de onda de pandeo depende solo de y , esta misma fórmula es válida para carcasas cilíndricas delgadas de espesor . ^[7] ${\displaystyle \sigma }$ ${\displaystyle L}$ ${\displaystyle c}$ ${\displaystyle h}$ ${\displaystyle \sigma }$ ${\displaystyle h}$ ${\displaystyle h}$

Teoría

Método de energía

A menudo es muy difícil determinar la carga de pandeo exacta en estructuras complejas utilizando la fórmula de Euler, debido a la dificultad de determinar la constante K. Por lo tanto, la carga de pandeo máxima a menudo se aproxima utilizando la conservación de energía y se la denomina método de energía en el análisis estructural.

El primer paso de este método es suponer un modo de desplazamiento y una función que represente ese desplazamiento. Esta función debe satisfacer las condiciones de contorno más importantes, como el desplazamiento y la rotación. Cuanto más precisa sea la función de desplazamiento, más preciso será el resultado.

El método supone que el sistema (la columna) es un sistema conservativo en el que la energía no se disipa en forma de calor, por lo tanto, la energía agregada a la columna por las fuerzas externas aplicadas se almacena en la columna en forma de energía de deformación.

$${\displaystyle U_{\text{applied}}=U_{\text{strain}}}$$

En este método, se utilizan dos ecuaciones (para pequeñas deformaciones) para aproximar la energía de "deformación" (la energía potencial almacenada como deformación elástica de la estructura) y la energía "aplicada" (el trabajo realizado en el sistema por fuerzas externas).

$${\displaystyle {\begin{aligned}U_{\text{strain}}&={\frac {E}{2}}\int I(x)(w_{xx}(x))^{2}\,\mathrm {d} x\\U_{\text{applied}}&={\frac {P_{\text{crit}}}{2}}\int (w_{x}(x))^{2}\,\mathrm {d} x\end{aligned}}}$$

donde es la función de desplazamiento y los subíndices y hacen referencia a la primera y segunda derivada del desplazamiento. ${\displaystyle w(x)}$ ${\displaystyle x}$ ${\displaystyle xx}$

Modelos de un solo grado de libertad

Utilizando el concepto de energía potencial total , , es posible identificar cuatro formas fundamentales de pandeo encontradas en modelos estructurales con un grado de libertad. Comenzamos expresando donde es la energía de deformación almacenada en la estructura, es la carga conservativa aplicada y es la distancia recorrida por en su dirección. Utilizando los axiomas de la teoría de la inestabilidad elástica, a saber, que el equilibrio es cualquier punto donde es estacionario con respecto a la coordenada que mide el grado(s) de libertad y que estos puntos solo son estables si es un mínimo local e inestables en caso contrario (por ejemplo, máximo o un punto de inflexión). ^[8] ${\displaystyle V}$ $${\displaystyle V=U-P\Delta }$$ ${\displaystyle U}$ ${\displaystyle P}$ ${\displaystyle \Delta }$ ${\displaystyle P}$ ${\displaystyle V}$ ${\displaystyle V}$

Estas cuatro formas de pandeo elástico son la bifurcación en nodo de silla o punto límite ; la bifurcación supercrítica o simétrica estable ; la bifurcación subcrítica o simétrica inestable ; y la bifurcación transcrítica o asimétrica . Todos estos ejemplos, excepto el primero, son una forma de bifurcación en horquilla . En las figuras siguientes se muestran modelos simples para cada uno de estos tipos de comportamiento de pandeo, junto con los diagramas de bifurcación asociados.

Ejemplos de ingeniería

Ruedas de bicicleta

Una rueda de bicicleta convencional consiste en una llanta delgada que se mantiene bajo una gran tensión de compresión mediante la tracción hacia adentro (aproximadamente normal) de un gran número de radios. Puede considerarse como una columna cargada que se ha doblado formando un círculo. Si la tensión de los radios aumenta más allá de un nivel seguro o si una parte de la llanta está sujeta a una cierta fuerza lateral, la rueda falla espontáneamente y adquiere una forma característica de sillín (a veces llamada "taco" o " pringle "), como una columna de Euler tridimensional. Si se trata de una deformación puramente elástica, la llanta recuperará su forma plana adecuada si se reduce la tensión de los radios o se aplica una fuerza lateral en la dirección opuesta.

Carreteras

El pandeo es un modo de falla en los materiales de pavimento , principalmente en el hormigón, ya que el asfalto es más flexible. El calor radiante del sol se absorbe en la superficie de la carretera, lo que hace que se expanda y obligue a las piezas adyacentes a empujarse entre sí. Si la tensión es suficiente, el pavimento puede levantarse y agrietarse sin previo aviso. Atravesar una sección pandeada puede ser desconcertante para los conductores de automóviles , como pasar por encima de un resalto a velocidades de autopista.

Vías del tren

Vías ferroviarias en los Países Bajos afectadas por el sol

De manera similar, las vías del tren también se expanden cuando se calientan y pueden fallar por pandeo, un fenómeno llamado torcedura solar . ^[9] Es más común que los rieles se muevan lateralmente, a menudo tirando de los durmientes subyacentes . ^[10]

La deformación por el sol puede hacer que los ferrocarriles reduzcan drásticamente la velocidad de los trenes, lo que provoca retrasos y cancelaciones. Esto se hace para evitar descarrilamientos. La intensificación de las olas de calor debido al cambio climático duplicó la cantidad de horas de retrasos relacionados con el calor en 2023, en comparación con 2018. ^[11]

Se consideró que estos accidentes estaban relacionados con la exposición al sol ( más información disponible en Lista de accidentes ferroviarios (2000-2009) ):

• 18 de abril de 2002 Descarrilamiento del tren Amtrak Auto-Train , fuera de las vías de CSX , cerca de Crescent City, Florida . ^[12]
• 29 de julio de 2002 Descarrilamiento de Amtrak Capitol Limited , fuera de las vías de CSX , cerca de Kensington, Maryland . ^[13]
• 8 de julio de 2010 Descarrilamiento del tren CSX en Waxhaw, Carolina del Norte . ^[14]
• 6 de julio de 2012 Descarrilamiento de tren de Metrorail de WMATA cerca de la estación West Hyattsville , Maryland . ^[15]

El 11 de julio de 2012, la Administración Federal de Ferrocarriles emitió un aviso de seguridad en el que alertaba a los operadores ferroviarios para que inspeccionaran las vías en busca de "condiciones propensas a deformaciones". El aviso incluía un breve resumen de cuatro descarrilamientos ocurridos entre el 23 de junio y el 4 de julio que parecían ser "incidentes relacionados con el calor". ^[16]

Tuberías y recipientes a presión

Las tuberías y los recipientes a presión sometidos a sobrepresión externa, causada por ejemplo por el enfriamiento del vapor dentro de la tubería y la condensación en agua con la consiguiente caída masiva de presión, corren el riesgo de deformarse debido a tensiones circunferenciales de compresión . Las reglas de diseño para el cálculo del espesor de pared requerido o de los anillos de refuerzo se encuentran en varios códigos de tuberías y recipientes a presión.

Vehículos aeroespaciales supersónicos e hipersónicos

El calentamiento aerotérmico puede provocar el pandeo de los paneles de superficie en vehículos aeroespaciales supersónicos e hipersónicos, como aviones de alta velocidad, cohetes y vehículos de reentrada. ^[17] Si el pandeo es causado por cargas aerotérmicas, la situación puede complicarse aún más por una mayor transferencia de calor en áreas donde la estructura se deforma hacia el campo de flujo. ^[18]

Véase también

• Carga crítica de Euler  : fórmula para cuantificar el pandeo de una columna bajo una carga dada
• Pandeo geométrico y material  : absorción y transmisión de neutrones por materiales de reactores nucleares
• Fórmula de Perry-Robertson
• Tensado de rieles
• Rigidez  : método para aumentar la rigidez y la integridad estructural de materiales u objetos.Pages displaying wikidata descriptions as a fallback
• Método de la madera  : método de análisis estructuralPages displaying wikidata descriptions as a fallback
• Pandeo de Yoshimura  : patrón de pandeo utilizado en ingeniería mecánica

Referencias

1. Bruhn, EF (1973). Análisis y diseño de estructuras de vehículos de vuelo . Indianápolis: Jacobs.
2. Elishakoff, I. Li YW. y Starnes, JH Jr., Problemas no clásicos en la teoría de la estabilidad elástica, Cambridge University Press, 2001, XVI +pp.336; ISBN 0-521-78210-4 
3. Kato, K. (1915). "Investigación matemática sobre los problemas mecánicos de las líneas de transmisión". Revista de la Sociedad Japonesa de Ingenieros Mecánicos . 19 : 41.
4. Ratzersdorfer, Julio (1936). Die Knickfestigkeit von Stäben und Stabwerken [ La resistencia al pandeo de miembros y marcos ] (en alemán). Vino, Austria: J. Springer. págs. 107-109. ISBN 978-3-662-24075-5.
5. Cox, Steven J.; C. Maeve McCarthy (1998). "La forma de la columna más alta". Revista SIAM sobre análisis matemático . 29 (3): 547–554. doi :10.1137/s0036141097314537.
6. Bulson, PS (1970). Teoría de placas planas . Chatto y Windus, Londres.
7. Lindberg, HE; ​​Florence, AL (1987). Pandeo dinámico por pulsos . Martinus Nijhoff Publishers . págs. 11–56, 297–298.
8. Thompson, JMT; Hunt, GW (1973). Una teoría general de la estabilidad elástica . Londres: John Wiley. ISBN 9780471859918.
9. Magill, Bobby (31 de julio de 2014). "Los descarrilamientos pueden aumentar a medida que el 'sol' dobla las vías". Climate Central . Consultado el 18 de julio de 2024 .
10. Li, Dingquing; Hyslip, James; Sussmann, Ted; Chrismer, Steven (2002). Geotecnia ferroviaria. CRC Press. pág. 430-431. ISBN 148228880X.
11. Kim, Minho (17 de julio de 2024). "Los pasajeros de Amtrak enfrentan demoras récord debido a condiciones climáticas extremas". New York Times . Consultado el 18 de julio de 2024 .
12. Descarrilamiento del tren Amtrak Auto P052-18 en la línea CSXT cerca de Crescent City, Florida, 18 de abril de 2002 (PDF) (Informe). Junta Nacional de Seguridad del Transporte. 5 de agosto de 2003. p. v . Consultado el 18 de julio de 2024 .
13. Braun, Stephen (30 de julio de 2002). «Los vagones de un tren de pasajeros se desploman por las vías sobrecalentadas». Los Angeles Times . Consultado el 18 de julio de 2024 .
14. "El calor podría deformar las vías del tren y provocar descarrilamientos". WIS 10 . Columbia, SC. ​​15 de julio de 2010 . Consultado el 18 de julio de 2024 .
15. Lucero, Kat (7 de julio de 2012). "Vía desalineada por el calor, 'causa probable' del descarrilamiento de la Línea Verde". DCist . American University Radio. Archivado desde el original el 4 de febrero de 2018 . Consultado el 21 de enero de 2019 .
16. Robert C. Lauby (16 de julio de 2012). Aviso de advertencia de seguridad (PDF) (Informe). Registro Federal. pág. 41881-41882 . Consultado el 18 de julio de 2024 .
17. Spottswood, S. Michael; Beberniss, Timothy J.; Eason, Thomas G.; Perez, Ricardo A.; Donbar, Jeffrey M.; Ehrhardt, David A.; Riley, Zachary B. (marzo de 2019). "Explorando la respuesta de un panel delgado y flexible a interacciones de capa límite turbulentas por choque". Journal of Sound and Vibration . 443 : 74–89. Bibcode :2019JSV...443...74S. doi : 10.1016/j.jsv.2018.11.035 . S2CID  125479249.
18. Daub, Dennis; Esser, Burkard; Gülhan, Ali (abril de 2020). "Experimentos sobre interacción fluido-estructura hipersónica de alta temperatura con deformación plástica". AIAA Journal . 58 (4): 1423–1431. Bibcode :2020AIAAJ..58.1423D. doi : 10.2514/1.J059150 .

Lectura adicional

• Timoshenko, SP ; Gere, JM (1961). Teoría de la estabilidad elástica (2.ª ed.). McGraw-Hill.
• Nenezich, M. (2004). "Mecánica del medio continuo termoplástico". Revista de estructuras aeroespaciales . 4 .
• Koiter, WT (1945). La estabilidad del equilibrio elástico (PDF) (Tesis doctoral).
• Rajesh, Dhakal; Maekawa, Koichi (2002). "Estabilidad de la armadura y fractura del hormigón de recubrimiento en elementos de hormigón armado". Journal of Structural Engineering . 128 (10): 1253–1262. doi :10.1061/(ASCE)0733-9445(2002)128:10(1253). hdl : 10092/4229 .
• Segui, Willian T. (2007). Steel Design (Cuarta edición). Estados Unidos: Thomson. ISBN 978-0-495-24471-4.
• Bruhn, EF (1973). Análisis y diseño de estructuras de vehículos de vuelo . Indianápolis: Jacobs.
• Elishakoff, I. (2004). Resolución del enigma del siglo XX en materia de estabilidad elástica . Singapur: World Scientific/Imperial College Press. ISBN 978-981-4583-53-4.

Enlaces externos

• La teoría completa y los resultados experimentales de ejemplo para columnas largas están disponibles como un documento PDF de 39 páginas en http://lindberglce.com/tech/buklbook.htm