
El pliegue de Miura (ミウラ折り, Miura-ori ) es un método para doblar una superficie plana, como una hoja de papel, en un área más pequeña. El pliegue recibe su nombre de su inventor, el astrofísico japonés Kōryō Miura . [1]
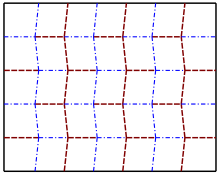
Los patrones de pliegues del pliegue de Miura forman una teselación de la superficie mediante paralelogramos . En una dirección, los pliegues se encuentran a lo largo de líneas rectas, y cada paralelogramo forma el reflejo especular de su vecino al otro lado de cada pliegue. En la otra dirección, los pliegues zigzaguean, y cada paralelogramo es la traslación de su vecino al otro lado del pliegue. Cada uno de los caminos en zigzag de los pliegues consiste únicamente en pliegues de montaña o de pliegues de valle , con montañas alternando con valles de un camino en zigzag al siguiente. Cada uno de los caminos rectos de los pliegues alterna entre pliegues de montaña y de valle. [2] El pliegue de Miura está relacionado con el pliegue de Kresling, el pliegue de Yoshimura y el pliegue hexagonal, y puede enmarcarse como una generalización de estos pliegues. [3]
El pliegue de Miura es una forma de origami rígido , lo que significa que el pliegue se puede realizar mediante un movimiento continuo en el que, en cada paso, cada paralelogramo es completamente plano. Esta propiedad permite que se utilice para plegar superficies hechas de materiales rígidos, lo que lo distingue del pliegue de Kresling y el pliegue de Yoshimura , que no se pueden plegar rígidamente y requieren deformaciones del panel para comprimirse a un estado compacto. [4] Por ejemplo, grandes conjuntos de paneles solares para satélites espaciales en el programa espacial japonés se han plegado en Miura antes del lanzamiento y luego se han extendido en el espacio. [5] [6] Un pliegue de Miura plegado se puede empaquetar en una forma compacta, y su espesor refleja solo el espesor del material plegado. El material plegado se puede desempaquetar en un movimiento tirando de sus extremos opuestos, y también se puede plegar juntando los dos extremos. En la aplicación de paneles solares, esta propiedad reduce la cantidad de motores necesarios para desplegar esta forma, lo que reduce el peso y la complejidad.
La Unidad Space Flyer de 1996 desplegó el conjunto 2D desde una configuración plegada de Miura. [7]
La estructura de membrana inflable del satélite SPROUT se lleva al espacio en el estado plegado de Miura y luego se despliega utilizando tubos inflables que a su vez se llevan al espacio en el estado plegado de Octágono. [8] [9]
Otras aplicaciones potenciales de este pliegue incluyen dispositivos quirúrgicos como stents y muebles plegables planos. [10]
Los investigadores de la Universidad de Friburgo utilizaron el pliegue de Miura para apilar películas de hidrogel , generando electricidad de manera similar a las anguilas eléctricas . El pliegue de Miura se utiliza para hacer que muchas partes de la pila entren en contacto entre sí simultáneamente. [11]