
Una partícula puntual , partícula ideal [1] o partícula puntual (a menudo escrita partícula puntual ) es una idealización de partículas muy utilizada en física . Su característica definitoria es que carece de extensión espacial ; al ser adimensional, no ocupa espacio . [2] Una partícula puntual es una representación apropiada de cualquier objeto siempre que su tamaño, forma y estructura sean irrelevantes en un contexto dado. Por ejemplo, desde una distancia suficiente, cualquier objeto de tamaño finito se verá y se comportará como un objeto puntual. Las masas puntuales y las cargas puntuales, que se analizan a continuación, son dos casos comunes. Cuando una partícula puntual tiene una propiedad aditiva, como masa o carga, a menudo se representa matemáticamente mediante una función delta de Dirac . En la mecánica clásica, no suele existir el concepto de rotación de partículas puntuales sobre su "centro".
En mecánica cuántica , el concepto de partícula puntual se complica por el principio de incertidumbre de Heisenberg , porque incluso una partícula elemental , sin estructura interna, ocupa un volumen distinto de cero. Por ejemplo, la órbita atómica de un electrón en el átomo de hidrógeno ocupa un volumen de ~10 −30 m 3 . Sin embargo, existe una distinción entre partículas elementales como los electrones o los quarks , que no tienen una estructura interna conocida, y partículas compuestas como los protones y los neutrones, cuyas estructuras internas están formadas por quarks. A las partículas elementales a veces se las llama "partículas puntuales" en referencia a su falta de estructura interna, pero esto es en un sentido diferente al que se analiza aquí.
Masa puntual ( masa puntual ) es el concepto, por ejemplo en física clásica , de un objeto físico (normalmente materia ) que tiene masa distinta de cero, y sin embargo explícita y específicamente es (o se piensa en él o se modela como) infinitesimal (infinitamente pequeño) en su volumen o dimensiones lineales . En la teoría de la gravedad , los objetos extensos pueden comportarse como puntuales incluso en su vecindad inmediata. Por ejemplo, los objetos esféricos que interactúan en el espacio tridimensional cuyas interacciones se describen mediante la gravitación newtoniana se comportan, siempre que no se toquen entre sí, de tal manera que toda su materia se concentrara en sus centros de masa . [3] De hecho, esto es cierto para todos los campos descritos por una ley del cuadrado inverso . [4] [5]

De manera similar a las masas puntuales, en el electromagnetismo los físicos discuten unacarga puntual , una partícula puntual con unacarga eléctrica.[6]Laecuacióndela electrostáticaesla ley de Coulomb, que describe la fuerza eléctrica entre dos cargas puntuales. Otro resultado,el teorema de Earnshaw, establece que una colección de cargas puntuales no se puede mantener en unade equilibrioúnicamente por la interacción electrostática de las cargas. Elcampo eléctricoasociado con una carga puntual clásica aumenta hasta el infinito a medida que la distancia desde la carga puntual disminuye hacia cero, lo que sugiere que el modelo ya no es preciso en este límite.
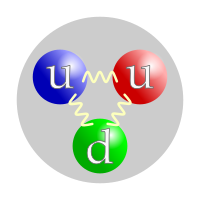
En mecánica cuántica , existe una distinción entre una partícula elemental (también llamada "partícula puntual") y una partícula compuesta . Una partícula elemental, como un electrón , un quark o un fotón , es una partícula sin estructura interna conocida. Mientras que una partícula compuesta, como un protón o un neutrón , tiene una estructura interna (véase la figura). Sin embargo, ni las partículas elementales ni las compuestas están localizadas espacialmente, debido al principio de incertidumbre de Heisenberg . El paquete de ondas de la partícula siempre ocupa un volumen distinto de cero. Por ejemplo, véase orbital atómico : El electrón es una partícula elemental, pero sus estados cuánticos forman patrones tridimensionales.
Sin embargo, hay buenas razones para que a una partícula elemental se la denomine partícula puntual. Incluso si una partícula elemental tiene un paquete de ondas deslocalizado, el paquete de ondas puede representarse como una superposición cuántica de estados cuánticos en los que la partícula está exactamente localizada. Además, las interacciones de la partícula pueden representarse como una superposición de interacciones de estados individuales que están localizados. Esto no es cierto para una partícula compuesta, que nunca puede representarse como una superposición de estados cuánticos exactamente localizados. Es en este sentido que los físicos pueden discutir el "tamaño" intrínseco de una partícula: el tamaño de su estructura interna, no el tamaño de su paquete de ondas. El "tamaño" de una partícula elemental, en este sentido, es exactamente cero.
Por ejemplo, para el electrón, la evidencia experimental muestra que el tamaño de un electrón es menor que10 −18 m . [7] Esto es consistente con el valor esperado de exactamente cero. (Esto no debe confundirse con el radio clásico del electrón , que, a pesar del nombre, no está relacionado con el tamaño real de un electrón).