En química , la hibridación orbital (o hibridación ) es el concepto de mezclar orbitales atómicos para formar nuevos orbitales híbridos (con energías, formas, etc. diferentes a las de los orbitales atómicos componentes) adecuados para el apareamiento de electrones para formar enlaces químicos en la teoría del enlace de valencia . Por ejemplo, en un átomo de carbono que forma cuatro enlaces simples, el orbital s de la capa de valencia se combina con tres orbitales p de la capa de valencia para formar cuatro mezclas sp 3 equivalentes en una disposición tetraédrica alrededor del carbono para unirse a cuatro átomos diferentes. Los orbitales híbridos son útiles para explicar la geometría molecular y las propiedades de enlace atómico y están dispuestos simétricamente en el espacio. Por lo general, los orbitales híbridos se forman mezclando orbitales atómicos de energías comparables. [1]
El químico Linus Pauling desarrolló por primera vez la teoría de la hibridación en 1931 para explicar la estructura de moléculas simples como el metano (CH 4 ) utilizando orbitales atómicos . [2] Pauling señaló que un átomo de carbono forma cuatro enlaces utilizando un orbital s y tres orbitales p, de modo que "se podría inferir" que un átomo de carbono formaría tres enlaces en ángulos rectos (utilizando orbitales p) y un cuarto enlace más débil utilizando el orbital s en alguna dirección arbitraria. En realidad, el metano tiene cuatro enlaces C–H de fuerza equivalente. El ángulo entre dos enlaces cualesquiera es el ángulo de enlace tetraédrico de 109°28' [3] (alrededor de 109,5°). Pauling supuso que en presencia de cuatro átomos de hidrógeno, los orbitales s y p forman cuatro combinaciones equivalentes a las que llamó orbitales híbridos . Cada híbrido se denota sp 3 para indicar su composición, y está dirigido a lo largo de uno de los cuatro enlaces C–H. [4] Este concepto fue desarrollado para sistemas químicos tan simples, pero luego se aplicó más ampliamente y hoy se considera una heurística eficaz para racionalizar las estructuras de compuestos orgánicos . Proporciona una imagen orbital simple equivalente a las estructuras de Lewis .
La teoría de la hibridación es una parte integral de la química orgánica , y uno de los ejemplos más convincentes son las reglas de Baldwin . Para dibujar mecanismos de reacción, a veces se necesita una imagen de enlace clásica con dos átomos compartiendo dos electrones. [5] La teoría de la hibridación explica el enlace en alquenos [6] y metano. [7] La cantidad de carácter p o carácter s, que se decide principalmente por la hibridación orbital, se puede utilizar para predecir de manera confiable propiedades moleculares como la acidez o la basicidad. [8]
Los orbitales son una representación modelo del comportamiento de los electrones dentro de las moléculas. En el caso de la hibridación simple, esta aproximación se basa en orbitales atómicos , similares a los obtenidos para el átomo de hidrógeno, el único átomo neutro para el que se puede resolver con exactitud la ecuación de Schrödinger . En átomos más pesados, como el carbono, el nitrógeno y el oxígeno, los orbitales atómicos utilizados son los orbitales 2s y 2p, similares a los orbitales de estado excitado del hidrógeno.
Se supone que los orbitales híbridos son mezclas de orbitales atómicos, superpuestos entre sí en diversas proporciones. Por ejemplo, en el metano , el orbital híbrido C que forma cada enlace carbono - hidrógeno consta de un 25% de carácter s y un 75% de carácter p y, por lo tanto, se describe como hibridado sp 3 (léase sp-tres ). La mecánica cuántica describe este híbrido como una función de onda sp 3 de la forma , donde N es una constante de normalización (aquí 1/2) y pσ es un orbital p dirigido a lo largo del eje CH para formar un enlace sigma . La relación de coeficientes (denotada λ en general) es en este ejemplo. Dado que la densidad electrónica asociada con un orbital es proporcional al cuadrado de la función de onda, la relación entre el carácter p y el carácter s es λ 2 = 3. El carácter p o el peso del componente p es N 2 λ 2 = 3/4.

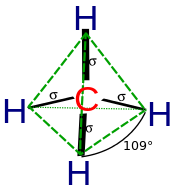
La hibridación describe la unión de átomos desde el punto de vista de un átomo. Para un carbono coordinado tetraédricamente (por ejemplo, metano CH 4 ), el carbono debería tener 4 orbitales dirigidos hacia los 4 átomos de hidrógeno.
La configuración del estado fundamental del carbono es 1s 2 2s 2 2p 2 o más, que se lee fácilmente:
Este diagrama sugiere que el átomo de carbono podría utilizar sus dos orbitales p individuales para formar dos enlaces covalentes con dos átomos de hidrógeno en una molécula de metileno (CH 2 ), con un ángulo de enlace hipotético de 90° correspondiente al ángulo entre dos orbitales p en el mismo átomo. Sin embargo, el verdadero ángulo H–C–H en el metileno singlete es de aproximadamente 102° [9] , lo que implica la presencia de cierta hibridación orbital.
El átomo de carbono también puede unirse a cuatro átomos de hidrógeno en el metano mediante una excitación (o promoción) de un electrón desde el orbital 2s doblemente ocupado al orbital 2p vacío, produciendo cuatro orbitales individualmente ocupados.
La energía liberada por la formación de dos enlaces adicionales compensa con creces la energía de excitación requerida, favoreciendo energéticamente la formación de cuatro enlaces CH.
Según la mecánica cuántica, la energía más baja se obtiene si los cuatro enlaces son equivalentes, lo que requiere que se formen a partir de orbitales equivalentes en el carbono. Se puede obtener un conjunto de cuatro orbitales equivalentes que son combinaciones lineales de las funciones de onda s y p de la capa de valencia (los orbitales del núcleo casi nunca participan en el enlace), [10] que son los cuatro híbridos sp 3 .
En CH 4 , cuatro orbitales híbridos sp 3 se superponen con orbitales 1s de hidrógeno , lo que produce cuatro enlaces σ (sigma) (es decir, cuatro enlaces covalentes simples) de igual longitud y fuerza.
La siguiente :

se traduce en:


Otros compuestos de carbono y otras moléculas pueden explicarse de manera similar. Por ejemplo, el eteno (C 2 H 4 ) tiene un doble enlace entre los carbonos.
En esta molécula, el carbono sp 2 se hibrida, porque se requiere un enlace π (pi) para el doble enlace entre los carbonos y solo se forman tres enlaces σ por átomo de carbono. En la hibridación sp 2, el orbital 2s se mezcla con solo dos de los tres orbitales 2p disponibles, generalmente denominados 2p x y 2p y . El tercer orbital 2p (2p z ) permanece sin hibridar.
formando un total de tres orbitales sp 2 con un orbital p restante. En el eteno, los dos átomos de carbono forman un enlace σ al superponer un orbital sp 2 de cada átomo de carbono. El enlace π entre los átomos de carbono perpendiculares al plano molecular se forma mediante superposición 2p–2p. Cada átomo de carbono forma enlaces covalentes C–H con dos hidrógenos mediante superposición s–sp 2 , todos con ángulos de enlace de 120°. Los enlaces hidrógeno-carbono son todos de igual fuerza y longitud, de acuerdo con los datos experimentales.

La unión química en compuestos como los alquinos con triples enlaces se explica por la hibridación sp. En este modelo, el orbital 2s se mezcla con solo uno de los tres orbitales p.
lo que da como resultado dos orbitales sp y dos orbitales p restantes. El enlace químico en el acetileno (etino) (C 2 H 2 ) consiste en una superposición sp–sp entre los dos átomos de carbono que forman un enlace σ y dos enlaces π adicionales formados por una superposición p–p. Cada carbono también se une al hidrógeno en una superposición σ s–sp en ángulos de 180°.

La hibridación ayuda a explicar la forma de las moléculas , ya que los ángulos entre enlaces son aproximadamente iguales a los ángulos entre orbitales híbridos. Esto contrasta con la teoría de repulsión de pares de electrones de la capa de valencia (VSEPR) , que se puede utilizar para predecir la geometría molecular basándose en reglas empíricas en lugar de teorías de enlaces de valencia o de orbitales. [11]
Como los orbitales de valencia de los elementos del grupo principal son los orbitales 1 s y 3 p con la regla del octeto correspondiente, se utiliza la hibridación sp x para modelar la forma de estas moléculas.
Como los orbitales de valencia de los metales de transición son los cinco orbitales d, uno s y tres orbitales p con la regla de los 18 electrones correspondiente , se utiliza la hibridación sp x d y para modelar la forma de estas moléculas. Estas moléculas tienden a tener múltiples formas correspondientes a la misma hibridación debido a los diferentes orbitales d involucrados. Un complejo plano cuadrado tiene un orbital p desocupado y, por lo tanto, tiene 16 electrones de valencia. [13]
En ciertos complejos de metales de transición con un bajo conteo de electrones d , los orbitales p están desocupados y se utiliza la hibridación sd x para modelar la forma de estas moléculas. [12] [14] [13]
En algunos libros de texto de química general, la hibridación se presenta para el grupo principal de coordinación número 5 y superior utilizando un esquema de "octeto expandido" con orbitales d propuesto por primera vez por Pauling. Sin embargo, dicho esquema ahora se considera incorrecto a la luz de los cálculos de química computacional.
En 1990, Eric Alfred Magnusson, de la Universidad de Nueva Gales del Sur , publicó un artículo que excluía definitivamente el papel de la hibridación de orbitales d en la unión en compuestos hipervalentes de elementos de segunda fila ( período 3 ), poniendo fin a un punto de controversia y confusión. Parte de la confusión se origina en el hecho de que las funciones d son esenciales en los conjuntos de base utilizados para describir estos compuestos (de lo contrario, se obtienen energías irrazonablemente altas y geometrías distorsionadas). Además, la contribución de la función d a la función de onda molecular es grande. Estos hechos se interpretaron incorrectamente como que los orbitales d deben estar involucrados en la unión. [15] [16]
A la luz de la química computacional , un mejor tratamiento sería invocar la resonancia de enlace sigma además de la hibridación, lo que implica que cada estructura de resonancia tiene su propio esquema de hibridación. Todas las estructuras de resonancia deben obedecer la regla del octeto . [17]
Si bien el modelo simple de hibridación orbital se utiliza comúnmente para explicar la forma molecular, la hibridación se utiliza de manera diferente cuando se calcula en programas de enlace de valencia modernos. En concreto, la hibridación no se determina a priori , sino que se optimiza variacionalmente para encontrar la solución de menor energía y luego se informa. Esto significa que se eliminan todas las restricciones artificiales, específicamente dos restricciones, sobre la hibridación orbital:
Esto significa que, en la práctica, los orbitales híbridos no se ajustan a las ideas simples que se enseñan comúnmente y, por lo tanto, en los artículos científicos computacionales se hace referencia a ellos simplemente como híbridos sp x , sp x d y o sd x para expresar su naturaleza en lugar de valores enteros más específicos.
Aunque los orbitales híbridos ideales pueden ser útiles, en realidad, la mayoría de los enlaces requieren orbitales de carácter intermedio. Esto requiere una extensión para incluir ponderaciones flexibles de orbitales atómicos de cada tipo (s, p, d) y permite una representación cuantitativa de la formación del enlace cuando la geometría molecular se desvía de los ángulos de enlace ideales. La cantidad de carácter p no está restringida a valores enteros; es decir, las hibridaciones como sp 2,5 también se describen fácilmente.
La hibridación de los orbitales de enlace está determinada por la regla de Bent : "El carácter atómico se concentra en los orbitales dirigidos hacia los sustituyentes electropositivos".
En el caso de las moléculas con pares solitarios, los orbitales de enlace son híbridos sp x isovalentes. Por ejemplo, los dos orbitales híbridos formadores de enlaces del oxígeno en el agua se pueden describir como sp 4.0 para dar el ángulo interorbital de 104.5°. [18] Esto significa que tienen un 20% de carácter s y un 80% de carácter p y no implica que un orbital híbrido se forme a partir de un orbital s y cuatro orbitales p en el oxígeno, ya que la subcapa 2p del oxígeno solo contiene tres orbitales p.
La hibridación de orbitales s y p para formar híbridos sp x efectivos requiere que tengan una extensión radial comparable. Mientras que los orbitales 2p son en promedio menos del 10% más grandes que los 2s, en parte atribuible a la falta de un nodo radial en orbitales 2p, los orbitales 3p que tienen un nodo radial, exceden a los orbitales 3s en un 20-33%. [19] La diferencia en la extensión de los orbitales s y p aumenta más abajo en un grupo. La hibridación de átomos en enlaces químicos se puede analizar considerando orbitales moleculares localizados, por ejemplo usando orbitales moleculares localizados naturales en un esquema de orbital de enlace natural (NBO). En metano , CH 4 , la relación p/s calculada es aproximadamente 3 consistente con la hibridación sp 3 "ideal" , mientras que para silano , SiH 4 , la relación p/s es más cercana a 2. Se observa una tendencia similar para los otros elementos 2p. La sustitución del flúor por hidrógeno reduce aún más la relación p/s. [20] Los elementos 2p presentan una hibridación casi ideal con orbitales híbridos ortogonales. Para los elementos del bloque p más pesados, esta suposición de ortogonalidad no se puede justificar. Estas desviaciones de la hibridación ideal fueron denominadas defectos de hibridación por Kutzelnigg . [21]
Sin embargo, los grupos VB computacionales como Gerratt, Cooper y Raimondi (SCVB) así como Shaik e Hiberty (VBSCF) van un paso más allá al argumentar que incluso para moléculas modelo como el metano, el etileno y el acetileno, los orbitales híbridos ya son defectuosos y no ortogonales, con hibridaciones como sp 1,76 en lugar de sp 3 para el metano. [22]
Un error conceptual relacionado con la hibridación orbital es que predice incorrectamente los espectros de fotoelectrones ultravioleta de muchas moléculas. Si bien esto es cierto si el teorema de Koopmans se aplica a los híbridos localizados, la mecánica cuántica requiere que la función de onda (en este caso ionizada) obedezca la simetría de la molécula, lo que implica resonancia en la teoría del enlace de valencia. Por ejemplo, en el metano, los estados ionizados (CH 4 + ) se pueden construir a partir de cuatro estructuras de resonancia que atribuyen el electrón expulsado a cada uno de los cuatro orbitales sp 3 . Una combinación lineal de estas cuatro estructuras, conservando el número de estructuras, conduce a un estado T 2 triplemente degenerado y un estado A 1 . [23] [24] La diferencia de energía entre cada estado ionizado y el estado fundamental sería la energía de ionización , que produce dos valores de acuerdo con los resultados experimentales.
Los orbitales de enlace formados a partir de orbitales atómicos híbridos pueden considerarse orbitales moleculares localizados, que pueden formarse a partir de los orbitales deslocalizados de la teoría de orbitales moleculares mediante una transformación matemática adecuada. Para las moléculas en el estado fundamental, esta transformación de los orbitales deja inalterada la función de onda total de muchos electrones. La descripción del orbital híbrido del estado fundamental es, por lo tanto, equivalente a la descripción del orbital deslocalizado para la energía total y la densidad electrónica del estado fundamental, así como a la geometría molecular que corresponde al valor mínimo de energía total.
Las moléculas con enlaces múltiples o pares solitarios múltiples pueden tener orbitales representados en términos de simetría sigma y pi u orbitales equivalentes. Los diferentes métodos de enlace de valencia utilizan cualquiera de las dos representaciones, que tienen funciones de onda de múltiples electrones totales matemáticamente equivalentes y están relacionadas por una transformación unitaria del conjunto de orbitales moleculares ocupados.
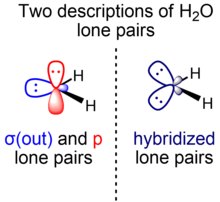
Para enlaces múltiples, la representación sigma-pi es la predominante en comparación con la representación orbital equivalente ( enlace doblado ). Por el contrario, para pares solitarios múltiples, la mayoría de los libros de texto utilizan la representación orbital equivalente. Sin embargo, la representación sigma-pi también se utiliza, como por Weinhold y Landis dentro del contexto de orbitales de enlace naturales , una teoría orbital localizada que contiene análogos modernizados de pares de enlace clásicos (enlace de valencia/estructura de Lewis) y pares solitarios. [25] Para la molécula de fluoruro de hidrógeno, por ejemplo, dos pares solitarios F son esencialmente orbitales p no hibridados, mientras que el otro es un orbital híbrido sp x . Una consideración análoga se aplica al agua (un par solitario O está en un orbital p puro, otro está en un orbital híbrido sp x ).