Número cuántico de espín

Parametrización de números cuánticos de espín y momento angular

En física y química, el número cuántico de espín es un número cuántico (designado s ) que describe el momento angular intrínseco (o momento angular de espín, o simplemente espín ) de un electrón u otra partícula . Tiene el mismo valor para todas las partículas del mismo tipo, como s = ⁠1/2⁠ para todos los electrones. Es un número entero para todos los bosones , como los fotones , y un entero semiimpar para todos los fermiones , como los electrones y los protones .

El componente del espín a lo largo de un eje específico está dado por el número cuántico magnético de espín , convencionalmente escrito m _s . ^{[1] [2]} El valor de m _s es el componente del momento angular de espín, en unidades de la constante de Planck reducida ħ , paralela a una dirección dada (convencionalmente etiquetada como el eje z ). Puede tomar valores que van desde + s a − s en incrementos enteros. Para un electrón, m _s puede ser ⁠++1/2⁠ o ⁠−+1/2⁠ .

Nomenclatura

Proyección cuántica de S sobre z para partículas de semiespín

La frase número cuántico de espín se refiere al momento angular de espín cuantificado . El símbolo s se utiliza para el número cuántico de espín, y m _s se describe como el número cuántico magnético de espín ^[3] o como el componente z del espín s _z . ^[4]

Tanto el espín total como el componente z del espín están cuantizados, lo que da lugar a dos números cuánticos: el espín y el imán de espín. ^[5] El número cuántico de espín (total) tiene un solo valor para cada partícula elemental. Algunos libros de texto introductorios de química describen m _s como el número cuántico de espín , ^{[6] [7]} y s no se menciona ya que su valor ⁠1/2⁠ es una propiedad fija del electrón; algunos incluso usan la variable s en lugar de m _s . ^[5]

Los dos números cuánticos de espín y son los análogos del momento angular de espín de los dos números cuánticos del momento angular orbital y . ^{[8] : 152} ${\displaystyle s}$ ${\displaystyle m_{s}}$ ${\displaystyle l}$ ${\displaystyle m_{l}}$

Los números cuánticos de espín se aplican también a sistemas de espines acoplados, como los átomos que pueden contener más de un electrón. Se utilizan símbolos en mayúsculas: S para el espín electrónico total y m _S o M _S para el componente del eje z . Un par de electrones en un estado singlete de espín tiene S = 0, y un par en el estado triplete tiene S = 1, con m _S = −1, 0 o +1. Los números cuánticos de espín nuclear se escriben convencionalmente I para el espín y m _I o M _I para el componente del eje z .

El nombre "spin" proviene de un giro geométrico del electrón alrededor de un eje, como lo propusieron Uhlenbeck y Goudsmit . Sin embargo, pronto se descubrió que esta imagen simplista era físicamente irreal, porque requeriría que los electrones giraran más rápido que la velocidad de la luz. ^[9] Por lo tanto, fue reemplazada por una descripción mecánica cuántica más abstracta.

Historia

Durante el período entre 1916 y 1925, se hicieron muchos progresos en relación con la disposición de los electrones en la tabla periódica . Para explicar el efecto Zeeman en el átomo de Bohr, Sommerfeld propuso que los electrones se basarían en tres "números cuánticos", n, k y m, que describían el tamaño de la órbita, la forma de la órbita y la dirección en la que apuntaba la órbita. ^[10] Irving Langmuir había explicado en su artículo de 1919 sobre los electrones en sus capas: "Rydberg ha señalado que estos números se obtienen de la serie . El factor dos sugiere una simetría doble fundamental para todos los átomos estables". ^[11] Esta configuración fue adoptada por Edmund Stoner , en octubre de 1924 en su artículo 'La distribución de electrones entre niveles atómicos' publicado en la revista Philosophical Magazine. ${\displaystyle N=2(1+2^{2}+2^{2}+3^{2}+3^{2}+4^{2})}$ ${\displaystyle 2n^{2}}$

El éxito cualitativo del esquema de números cuánticos de Sommerfeld no logró explicar el efecto Zeeman en intensidades de campo magnético débiles, el efecto Zeeman anómalo . En diciembre de 1924, Wolfgang Pauli demostró que el momento angular del electrón central no estaba relacionado con el efecto como se había asumido previamente. ^{[12] : 563} En cambio, propuso que solo los electrones "ligeros" externos determinaban el momento angular y planteó la hipótesis de que esto requería un cuarto número cuántico con un valor bivalente. ^[13] Este cuarto número cuántico se convirtió en el número cuántico magnético de espín.

Espín electrónico

Un giro- 1 /2La partícula se caracteriza por un número cuántico de momento angular para espín s = 1 /2⁠ . En las soluciones de la ecuación de Schrödinger-Pauli , el momento angular se cuantifica de acuerdo con este número, de modo que la magnitud del momento angular de espín es

$${\displaystyle \|{\mathbf {S}}\|=\hbar {\sqrt {s(s+1)}}={\tfrac {\sqrt {3}}{2}}\ \hbar ~.}$$

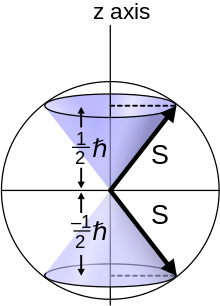
La estructura fina del espectro del hidrógeno se observa como un doblete correspondiente a dos posibilidades para el componente z del momento angular, donde para cualquier dirección dada z : $${\displaystyle s_{z}=\pm {\tfrac {1}{2}}\hbar ~.}$$

cuya solución tiene sólo dos componentes z posibles para el electrón. En el electrón, las dos orientaciones de espín diferentes se denominan a veces "spin-up" o "spin-down".

La propiedad de espín de un electrón daría lugar al momento magnético , que era un requisito para el cuarto número cuántico.

El vector del momento magnético del espín de un electrón viene dado por:

$${\displaystyle \ {\boldsymbol {\mu }}_{\text{s}}=-{\frac {e}{\ 2m\ }}\ g_{\text{s}}\ {\mathbf {S}}\ }$$

donde es la carga del electrón , es la masa del electrón y es el factor g del espín del electrón , que es aproximadamente 2,0023. Su proyección en el eje z viene dada por el número cuántico magnético del espín según: ${\displaystyle -e}$ ${\displaystyle m}$ ${\displaystyle g_{\text{s}}}$ ${\displaystyle m_{\text{s}}}$

$${\displaystyle \mu _{z}=-m_{\text{s}}\ g_{\text{s}}\ \mu _{\mathsf {B}}=\pm {\tfrac {1}{2}}\ g_{\text{s}}\ \mu _{\mathsf {B}}\ }$$

¿Dónde está el magnetón de Bohr ? ${\displaystyle \ \mu _{\mathsf {B}}\ }$

Cuando los átomos tienen un número par de electrones, el espín de cada electrón en cada orbital tiene una orientación opuesta a la de su(s) vecino(s) inmediato(s). Sin embargo, muchos átomos tienen un número impar de electrones o una disposición de electrones en la que hay un número desigual de orientaciones de "espín hacia arriba" y "espín hacia abajo". Se dice que estos átomos o electrones tienen espines desapareados que se detectan en la resonancia de espín electrónico .

Giro nuclear

Los núcleos atómicos también tienen espines. El espín nuclear I es una propiedad fija de cada núcleo y puede ser un número entero o semientero. El componente m _I del espín nuclear paralelo al eje z puede tener (2 I + 1) valores I , I –1, ..., –I . Por ejemplo, un núcleo ^{de 14} N tiene I = 1, de modo que hay 3 posibles orientaciones relativas al eje z , correspondientes a los estados m _I = +1, 0 y −1. ^[14]

Los espines I de diferentes núcleos se interpretan utilizando el modelo de capas nucleares . Los núcleos pares-pares con números pares de protones y neutrones, como 12 C y 16 O , tienen espín cero. Los núcleos con número másico impar tienen espines semienteros, como ⁠3/ 2 ⁠ por 7 Li , ⁠ 1 /2⁠ por 13 C y ⁠5/ 2 ⁠ para 17 O , que generalmente corresponde al momento angular del último nucleón añadido. Los núcleos impar-impares con números impares tanto de protones como de neutrones tienen espines enteros, como 3 para 10 B y 1 para 14 N . ^[15] Los valores de espín nuclear para un isótopo dado se encuentran en las listas de isótopos para cada elemento. (Véase isótopos de oxígeno , isótopos de aluminio , etc. etc.)

Detección de giro

Cuando se examinan las líneas del espectro del hidrógeno con una resolución muy alta, se descubre que son dobletes muy próximos entre sí. Esta división se denomina estructura fina y fue una de las primeras evidencias experimentales del espín del electrón. La observación directa del momento angular intrínseco del electrón se logró en el experimento de Stern-Gerlach .

Experimento de Stern-Gerlach

La teoría de la cuantificación espacial del momento de espín de los electrones de los átomos situados en el campo magnético debía demostrarse experimentalmente. En 1922 (dos años antes de que se creara la descripción teórica del espín), Otto Stern y Walter Gerlach la observaron en el experimento que realizaron.

Los átomos de plata se evaporaron utilizando un horno eléctrico en el vacío. Utilizando rendijas delgadas, los átomos fueron guiados hacia un haz plano y el haz pasó a través de un campo magnético no homogéneo antes de colisionar con una placa metálica. Las leyes de la física clásica predicen que la colección de átomos de plata condensados ​​en la placa debe formar una línea sólida delgada con la misma forma que el haz original. Sin embargo, el campo magnético no homogéneo hizo que el haz se dividiera en dos direcciones separadas, creando dos líneas en la placa metálica.

El fenómeno se puede explicar con la cuantificación espacial del momento de espín. En los átomos, los electrones están emparejados de tal manera que uno gira hacia arriba y el otro hacia abajo, neutralizando el efecto de su espín sobre la acción del átomo en su conjunto. Pero en la capa de valencia de los átomos de plata, hay un solo electrón cuyo espín permanece desequilibrado.

El espín desequilibrado crea un momento magnético de espín , lo que hace que el electrón actúe como un imán muy pequeño. A medida que los átomos pasan a través del campo magnético no homogéneo, el momento de fuerza en el campo magnético influye en el dipolo del electrón hasta que su posición coincide con la dirección del campo más fuerte. El átomo sería entonces atraído hacia o lejos del campo magnético más fuerte una cantidad específica, dependiendo del valor del espín del electrón de valencia. Cuando el espín del electrón es ++ 1 /2⁠ el átomo se aleja del campo más fuerte, y cuando el giro es ⁠−+ 1 /2El átomo se mueve hacia él. De esta manera , el haz de átomos de plata se divide mientras viaja a través del campo magnético no homogéneo, según el espín del electrón de valencia de cada átomo.

En 1927, Phipps y Taylor realizaron un experimento similar, utilizando átomos de hidrógeno con resultados similares. Más tarde, los científicos realizaron experimentos utilizando otros átomos que solo tenían un electrón en su capa de valencia: ( cobre , oro , sodio , potasio ). En cada ocasión se formaron dos líneas en la placa metálica.

El núcleo atómico también puede tener espín, pero los protones y neutrones son mucho más pesados ​​que los electrones (unas 1.836 veces más pesados ​​que ellos) y el momento dipolar magnético es inversamente proporcional a la masa. Por lo tanto, el momento dipolar magnético nuclear es mucho menor que el del átomo entero. Este pequeño dipolo magnético fue medido posteriormente por Stern, Frisch y Easterman.

Resonancia paramagnética electrónica

En el caso de átomos o moléculas con un electrón desapareado, también se pueden observar transiciones en un campo magnético en las que solo cambia el número cuántico de espín, sin cambio en el orbital del electrón ni en los otros números cuánticos. Este es el método de resonancia paramagnética electrónica (EPR) o resonancia de espín electrónico (ESR), utilizado para estudiar radicales libres . Dado que solo cambia la interacción magnética del espín, el cambio de energía es mucho menor que en las transiciones entre orbitales, y los espectros se observan en la región de microondas .

Relación con los vectores de espín

Para una solución tanto de la ecuación de Pauli no relativista como de la ecuación de Dirac relativista , el momento angular cuantificado (ver número cuántico del momento angular ) se puede escribir como: donde $${\displaystyle \Vert \mathbf {s} \Vert ={\sqrt {s\,(s+1)\,}}\,\hbar }$$

• ${\displaystyle \mathbf {s} }$es el vector de espín cuantificado o espinor
• ${\displaystyle \Vert \mathbf {s} \Vert }$es la norma del vector de espín
• s es el número cuántico de espín asociado con el momento angular de espín
• ${\displaystyle \hbar }$es la constante de Planck reducida .

Dada una dirección arbitraria z (generalmente determinada por un campo magnético externo), la proyección de espín z está dada por

${\displaystyle s_{z}=m_{s}\,\hbar }$

donde m _s es el número cuántico de espín magnético , que va de − s a + s en pasos de uno. Esto genera 2  s + 1 valores diferentes de m _s .

Los valores permitidos para s son números enteros no negativos o semienteros . Los fermiones tienen valores semienteros, incluidos el electrón , el protón y el neutrón , que tienen s = ⁠+ + 1 /2⁠ . Los bosones como el fotón y todos los mesones ) tienen valores de espín enteros.

Álgebra

La teoría algebraica del espín es una copia exacta del momento angular en la teoría de la mecánica cuántica. ^[16] En primer lugar, el espín satisface la relación de conmutación fundamental : donde es el símbolo de Levi-Civita (antisimétrico) . Esto significa que es imposible conocer dos coordenadas del espín al mismo tiempo debido a la restricción del principio de incertidumbre . $${\displaystyle \ [S_{i},S_{j}]=i\ \hbar \ \epsilon _{ijk}\ S_{k}\ ,}$$ $${\displaystyle \ \left[S_{i},S^{2}\right]=0\ }$$ ${\displaystyle \ \epsilon _{ijk}\ }$

A continuación, los vectores propios de y satisfacen: donde son los operadores de escalera (o de "elevación" y "descenso"). ${\displaystyle \ S^{2}\ }$ ${\displaystyle \ S_{z}\ }$ $${\displaystyle \ S^{2}\ |s,m_{s}\rangle ={\hbar }^{2}\ s(s+1)\ |s,m_{s}\rangle \ }$$ $${\displaystyle \ S_{z}\ |s,m_{s}\rangle =\hbar \ m_{s}\ |s,m_{s}\rangle \ }$$ $${\displaystyle \ S_{\pm }\ |s,m_{s}\rangle =\hbar \ {\sqrt {s(s+1)-m_{s}(m_{s}\pm 1)\ }}\;|s,m_{s}\pm 1\rangle \ }$$ ${\displaystyle \ S_{\pm }=S_{x}\pm iS_{y}\ }$

Niveles de energía de la ecuación de Dirac

En 1928, Paul Dirac desarrolló una ecuación de onda relativista , ahora denominada ecuación de Dirac , que predijo correctamente el momento magnético del espín y, al mismo tiempo, trató al electrón como una partícula puntual. Al resolver la ecuación de Dirac para los niveles de energía de un electrón en el átomo de hidrógeno, los cuatro números cuánticos, incluido s, se dieron de forma natural y coincidieron bien con el experimento.

Giro total de un átomo o molécula

En algunos átomos, los espines de varios electrones desapareados ( s ₁ , s ₂ , ...) están acoplados para formar un número cuántico de espín total S . ^{[17] [18]} Esto ocurre especialmente en átomos ligeros (o en moléculas formadas solo por átomos ligeros) cuando el acoplamiento espín-órbita es débil en comparación con el acoplamiento entre espines o el acoplamiento entre momentos angulares orbitales , una situación conocida como acoplamiento L S porque L y S son constantes de movimiento . Aquí L es el número cuántico de momento angular orbital total . ^[18]

Para átomos con un S bien definido , la multiplicidad de un estado se define como 2 S + 1. Esto es igual al número de diferentes valores posibles del momento angular total (orbital más espín) J para una combinación dada ( L , S ), siempre que S ≤ L (el caso típico). Por ejemplo, si S = 1, hay tres estados que forman un triplete . Los valores propios de S _z para estos tres estados son +1ħ, 0 y −1ħ . ^[17] El término símbolo de un estado atómico indica sus valores de L , S y J .

Como ejemplos, los estados fundamentales tanto del átomo de oxígeno como de la molécula de dioxígeno tienen dos electrones desapareados y, por lo tanto, son estados tripletes. El estado atómico se describe con el símbolo ³ P y el estado molecular con el símbolo ³ Σ .^-
_sol.

Véase también

• Número cuántico del momento angular total
• Espectroscopia rotacional
• Mecánica cuántica básica

Referencias

1. Pauling, Linus (1960). La naturaleza del enlace químico y la estructura de las moléculas y los cristales: una introducción a la química estructural moderna . Ithaca, NY: Cornell University Press. ISBN 0-8014-0333-2.OCLC  545520 .
2. "ISO 80000-10:2019". Organización Internacional de Normalización . Consultado el 15 de septiembre de 2019 .
3. Atkins, Peter; de Paula, Julio (2006). Química física de Atkins (8.ª ed.). WH Freeman. pág. 308. ISBN 0-7167-8759-8.
4. Banwell, Colin N.; McCash, Elaine M. (1994). Fundamentos de espectroscopia molecular . McGraw-Hill. pág. 135. ISBN. 0-07-707976-0.
5. Perrino, Charles T.; Peterson, Donald L. (1989). "¿Otro número cuántico?". J. Chem. Educ . 66 (8): 623. Bibcode :1989JChEd..66..623P. doi :10.1021/ed066p623. ISSN  0021-9584.
6. Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). Química general (8.ª ed.). Prentice Hall. pág. 333. ISBN 0-13-014329-4.
7. Whitten, Kenneth W.; Galley, Kenneth D.; Davis, Raymond E. (1992). Química general (4.ª ed.). Saunders College Publishing. pág. 196. ISBN 0-03-072373-6.
8. Karplus, Martin, y Porter, Richard Needham. Átomos y moléculas. Estados Unidos, WA Benjamin, 1970.
9. Halpern, Paul (21 de noviembre de 2017). «Spin: la propiedad cuántica que debería haber sido imposible». Forbes . Comienza con una explosión. Archivado desde el original el 10 de marzo de 2018. Consultado el 10 de marzo de 2018 .
10. Manjit Kumar, Quantum: Einstein, Bohr y el gran debate sobre la naturaleza de la realidad, 2008.
11. Langmuir, Irving (1919). "La disposición de los electrones en átomos y moléculas". Revista del Instituto Franklin . 187 (3): 359–362. doi :10.1016/S0016-0032(19)91097-0.
12. Giulini, Domenico (septiembre de 2008). "El espín del electrón o "doble valor clásicamente no descriptible"". Estudios de historia y filosofía de la ciencia, parte B: Estudios de historia y filosofía de la física moderna . 39 (3): 557–578. arXiv : 0710.3128 . Bibcode :2008SHPMP..39..557G. doi :10.1016/j.shpsb.2008.03.005. hdl :11858/00-001M-0000-0013-13C8-1. S2CID:  15867039.
13. Wolfgang Pauli. Principio de exclusión y mecánica cuántica. Conferencia Nobel pronunciada el 13 de diciembre de 1946 con ocasión del Premio Nobel de Física de 1945.
14. Atkins, Peter; de Paula, Julio (2006). Química física de Atkins (8.ª ed.). WH Freeman. pág. 515. ISBN 0-7167-8759-8.
15. Cottingham, WN; Greenwood, DA (1986). Introducción a la física nuclear . Cambridge University Press. pp. 36, 57. ISBN 0-521-31960-9.
16. David J. Griffiths , Introducción a la mecánica cuántica (libro) , Oregón, Reed College, 2018, 166 p. ISBN 9781107189638 . 
17. Merzbacher, E. (1998). Mecánica cuántica (3.ª ed.). John Wiley. pp. 430–431. ISBN 0-471-88702-1.
18. Atkins, P. ; de Paula, J. (2006). Química física (8.ª ed.). WH Freeman. pág. 352. ISBN 0-7167-8759-8.

Enlaces externos

• Weiss, Michael (2001). "Tratamiento completo del espín, incluidos los orígenes, la evolución de la teoría del espín y los detalles de las ecuaciones del espín". Departamento de Matemáticas . UC Riverside .