Método multired

En análisis numérico , un método multicuadrícula ( método MG ) es un algoritmo para resolver ecuaciones diferenciales utilizando una jerarquía de discretizaciones . Son un ejemplo de una clase de técnicas llamadas métodos de multiresolución , muy útiles en problemas que exhiben múltiples escalas de comportamiento. Por ejemplo, muchos métodos de relajación básicos exhiben diferentes tasas de convergencia para componentes de longitud de onda corta y larga, lo que sugiere que estas diferentes escalas deben tratarse de manera diferente, como en un enfoque de análisis de Fourier para redes múltiples. ^[1] Los métodos MG se pueden utilizar como solucionadores y precondicionadores .

La idea principal de multigrid es acelerar la convergencia de un método iterativo básico (conocido como relajación, que generalmente reduce el error de longitud de onda corta) mediante una corrección global de la aproximación de la solución de cuadrícula fina de vez en cuando, lograda resolviendo un problema aproximado . El problema grueso, aunque más barato de resolver, es similar al problema de la rejilla fina en que también tiene errores de longitud de onda corta y larga. También se puede solucionar mediante una combinación de relajación y apelación a rejillas aún más toscas. Este proceso recursivo se repite hasta que se alcanza una cuadrícula donde el costo de la solución directa es insignificante en comparación con el costo de un barrido de relajación en la cuadrícula fina. Este ciclo de múltiples redes generalmente reduce todos los componentes del error en una cantidad fija limitada muy por debajo de uno, independientemente del tamaño fino de la malla de la red. La aplicación típica de multigrid es la solución numérica de ecuaciones diferenciales parciales elípticas en dos o más dimensiones. ^[2]

Los métodos multired se pueden aplicar en combinación con cualquiera de las técnicas de discretización comunes. Por ejemplo, el método de elementos finitos puede reformularse como un método multicuadrícula. ^[3] En estos casos, los métodos multired se encuentran entre las técnicas de solución más rápidas que se conocen en la actualidad. A diferencia de otros métodos, los métodos multigrid son generales porque pueden tratar regiones y condiciones de contorno arbitrarias . No dependen de la separabilidad de las ecuaciones ni de otras propiedades especiales de la ecuación. También se han utilizado ampliamente para sistemas de ecuaciones no simétricos y no lineales más complicados, como las ecuaciones de elasticidad de Lamé o las ecuaciones de Navier-Stokes . ^[4]

Algoritmo

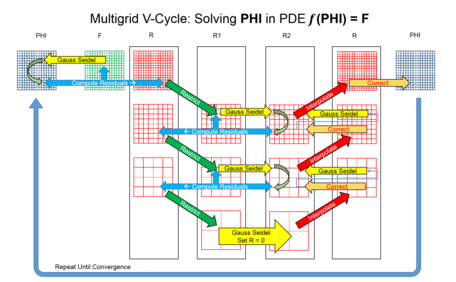
Existen muchas variaciones de algoritmos multigrid, pero las características comunes son que se considera una jerarquía de discretizaciones (grids). Los pasos importantes son: ^[5]^[6]

Suavizado : reducción de errores de alta frecuencia, por ejemplo utilizando algunas iteraciones del método Gauss-Seidel .
Cálculo residual : cálculo del error residual después de las operaciones de suavizado.
Restricción : reducir la resolución del error residual a una cuadrícula más gruesa.
Interpolación o prolongación : interpolar una corrección calculada en una cuadrícula más gruesa en una cuadrícula más fina.
Corrección : agregar una solución de rejilla más gruesa de forma prolongada a la rejilla más fina.

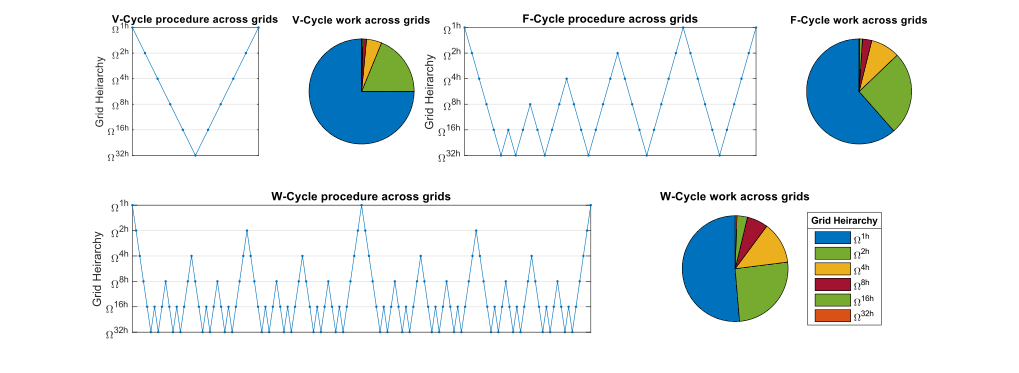
Hay muchas opciones de métodos multired con diferentes compensaciones entre la velocidad de resolución de una única iteración y la tasa de convergencia con dicha iteración. Los 3 tipos principales son V-Cycle, F-Cycle y W-Cycle. Estos se diferencian en qué y cuántos ciclos de grano grueso se realizan por iteración fina. El algoritmo V-Cycle ejecuta un V-Cycle de grano grueso. F-Cycle realiza un ciclo V de grano grueso seguido de un ciclo F de grano grueso, mientras que cada ciclo W realiza dos ciclos W de grano grueso por iteración. Para un problema 2D discreto , el ciclo F tarda un 83% más en calcularse que una iteración del ciclo V, mientras que una iteración del ciclo W tarda un 125% más. Si el problema se configura en un dominio 3D, entonces una iteración del ciclo F y una iteración del ciclo W toman aproximadamente un 64% y un 75% más de tiempo respectivamente que una iteración del ciclo V ignorando los gastos generales . Normalmente, el ciclo W produce una convergencia similar al ciclo F. Sin embargo, en casos de problemas de convección-difusión con números de Péclet altos , el ciclo W puede mostrar superioridad en su tasa de convergencia por iteración sobre el ciclo F. La elección de operadores de suavizado es extremadamente diversa, ya que incluyen métodos subespaciales de Krylov y pueden preacondicionarse .

Cualquier iteración de ciclo geométrico de múltiples cuadrículas se realiza en una jerarquía de cuadrículas y, por lo tanto, se puede codificar mediante recursividad. Dado que la función se llama a sí misma con parámetros de menor tamaño (más gruesos), la cuadrícula más gruesa es donde se detiene la recursividad. En los casos en los que el sistema tiene un número de condición alto , el procedimiento de corrección se modifica de modo que solo una fracción de la solución de rejilla más gruesa prolongada se agrega a la rejilla más fina.

Costo computacional [ cita necesaria ]

Suponiendo una configuración de problema bidimensional, el cálculo se mueve a través de la jerarquía de la red de manera diferente para varios ciclos de múltiples redes.

Este enfoque tiene la ventaja sobre otros métodos de que a menudo escala linealmente con la cantidad de nodos discretos utilizados. En otras palabras, puede resolver estos problemas con una precisión determinada en un número de operaciones que es proporcional al número de incógnitas.

Supongamos que tenemos una ecuación diferencial que se puede resolver aproximadamente (con una precisión determinada) en una cuadrícula con una densidad de puntos de cuadrícula determinada . Supongamos además que se puede obtener una solución en cualquier rejilla con un esfuerzo dado a partir de una solución en una rejilla más gruesa . Aquí, es la proporción de puntos de la cuadrícula en las cuadrículas "vecinas" y se supone que es constante en toda la jerarquía de la cuadrícula, y es una constante que modela el esfuerzo de calcular el resultado para un punto de la cuadrícula. $i$ ${\ Displaystyle N_ {i}}$ ${\ Displaystyle N_ {i}}$ $W_{i}=\rho KN_{i}$ $i+1$ $\rho =N_{i+1}/N_{i}<1$ $K$

Luego se obtiene la siguiente relación de recurrencia para el esfuerzo de obtener la solución en la red : $k$

W_{k}=W_{k+1}+\rho KN_{k}

Y en particular, encontramos para la cuadrícula más fina que ${\ Displaystyle N_ {1}}$

W_{1}=W_{2}+\rho KN_{1}

Combinando estas dos expresiones (y usando ) se obtiene $N_{k}=\rho ^{k-1}N_{1}$

W_{1}=KN_{1}\sum _{p=0}^{n}\rho ^{p}

Usando la serie geométrica , encontramos (para finitos ) $n$

W_{1}<KN_{1}{\frac {1}{1-\rho }}

es decir, se puede obtener una solución a tiempo. Cabe mencionar que existe una excepción a la red múltiple de ciclo W utilizada en un problema 1D; resultaría en complejidad. ^[^{cita necesaria}^] $O(N)$ $O(N)$ $O(Nlog(N))$

Preacondicionamiento multired

Se puede utilizar un método multicuadrícula con una tolerancia intencionalmente reducida como precondicionador eficiente para un solucionador iterativo externo, por ejemplo, ^[7] La solución aún se puede obtener a tiempo, así como en el caso en que se utiliza el método multicuadrícula como solucionador. El preacondicionamiento de redes múltiples se utiliza en la práctica incluso para sistemas lineales, normalmente con un ciclo por iteración, por ejemplo, en Hypre . Su principal ventaja frente a un solucionador puramente multired es particularmente clara para problemas no lineales, por ejemplo, problemas de valores propios . $O(N)$

Si la matriz de la ecuación original o un problema de valores propios es definida positiva simétrica (SPD), el precondicionador comúnmente se construye para que también sea SPD, de modo que aún se puedan usar los métodos iterativos de gradiente conjugado (CG) estándar. Tales restricciones de SPD impuestas pueden complicar la construcción del preacondicionador, por ejemplo, requiriendo un suavizado previo y posterior coordinado. Sin embargo, se ha demostrado que los métodos precondicionados de descenso más pronunciado y CG flexible para sistemas lineales SPD y LOBPCG para problemas de valores propios simétricos ^[8] son robustos si el precondicionador no es SPD.

Preacondicionador Bramble–Pasciak–Xu

Descrito originalmente en el doctorado de Xu. Tesis ^[9] y posteriormente publicada en Bramble-Pasciak-Xu, ^[10] el precondicionador BPX es uno de los dos principales enfoques multired (el otro es el algoritmo multired clásico como el ciclo V) para resolver sistemas algebraicos a gran escala. que surgen de la discretización de modelos en ciencia e ingeniería descritos por ecuaciones diferenciales parciales. En vista del marco de corrección subespacial, ^[11] el preacondicionador BPX es un método de corrección subespacial paralelo, mientras que el ciclo V clásico es un método de corrección subespacial sucesivo. Se sabe que el preacondicionador BPX es naturalmente más paralelo y, en algunas aplicaciones, más robusto que el método clásico de multirredes de ciclo V. El método ha sido ampliamente utilizado por investigadores y profesionales desde 1990.

Métodos multired generalizados.

Los métodos multigrid se pueden generalizar de muchas maneras diferentes. Se pueden aplicar de forma natural en una solución de ecuaciones diferenciales parciales parabólicas en pasos de tiempo , o se pueden aplicar directamente a ecuaciones diferenciales parciales dependientes del tiempo . ^[12] Se están realizando investigaciones sobre técnicas multinivel para ecuaciones diferenciales parciales hiperbólicas . ^[13] Los métodos multicuadrícula también se pueden aplicar a ecuaciones integrales , o para problemas de física estadística . ^[14]

Otro conjunto de métodos multiresolución se basa en wavelets . Estos métodos wavelet se pueden combinar con métodos multigrid. ^[15]^[16] Por ejemplo, un uso de las wavelets es reformular el enfoque de elementos finitos en términos de un método multinivel. ^[17]

La multicuadrícula adaptativa exhibe un refinamiento de malla adaptativo , es decir, ajusta la cuadrícula a medida que avanza el cálculo, de una manera que depende del cálculo mismo. ^[18] La idea es aumentar la resolución de la red sólo en las regiones de la solución donde sea necesario.

Multired algebraica (AMG)

Extensiones prácticamente importantes de los métodos multired incluyen técnicas en las que no se utiliza ninguna ecuación diferencial parcial ni antecedentes de problemas geométricos para construir la jerarquía multinivel. ^[19] Estos métodos algebraicos multired (AMG) construyen su jerarquía de operadores directamente a partir de la matriz del sistema. En el AMG clásico, los niveles de la jerarquía son simplemente subconjuntos de incógnitas sin ninguna interpretación geométrica. (De manera más general, las incógnitas de cuadrícula gruesa pueden ser combinaciones lineales particulares de incógnitas de cuadrícula fina). Por lo tanto, los métodos AMG se convierten en solucionadores de caja negra para ciertas clases de matrices dispersas . AMG se considera ventajoso principalmente cuando la multirrejilla geométrica es demasiado difícil de aplicar, ^[20] pero a menudo se utiliza simplemente porque evita la codificación necesaria para una verdadera implementación de multirrejilla. Si bien el AMG clásico se desarrolló primero, un método algebraico relacionado se conoce como agregación suavizada (SA).

En un artículo general ^[21] de Jinchao Xu y Ludmil Zikatanov, los métodos de "multired algebraica" se entienden desde un punto de vista abstracto. Desarrollaron un marco unificado y los métodos algebraicos de múltiples redes existentes se pueden derivar de manera coherente. Se derivó una teoría abstracta sobre cómo construir espacios gruesos óptimos y espacios cuasióptimos. Además, demostraron que, bajo supuestos apropiados, el método abstracto AMG de dos niveles converge uniformemente con respecto al tamaño del sistema lineal, la variación del coeficiente y la anisotropía. Su marco abstracto cubre la mayoría de los métodos AMG existentes, como el AMG clásico, el AMG de minimización de energía, el AMG de agregación suavizado y sin suavizar y el AMGe espectral.

Métodos multigrid en el tiempo.

También se han adoptado métodos multired para la solución de problemas de valor inicial . ^[22] De particular interés aquí son los métodos multigrid paralelos en el tiempo: ^[23] a diferencia de los métodos clásicos de Runge-Kutta o lineales de varios pasos , pueden ofrecer concurrencia en dirección temporal. El conocido método de integración en tiempo paralelo de Parareal también puede reformularse como una red múltiple en el tiempo de dos niveles.

Multigrid para problemas casi singulares

Surgen problemas casi singulares en una serie de importantes aplicaciones físicas y de ingeniería. Un ejemplo simple pero importante de problemas casi singulares se puede encontrar en la formulación de desplazamiento de la elasticidad lineal para materiales casi incompresibles. Normalmente, el principal problema para resolver sistemas casi singulares se reduce a tratar al operador casi singular dado por de manera robusta con respecto al parámetro positivo, pero pequeño . Aquí hay un operador semidefinido simétrico con un espacio nulo grande , mientras que es un operador definido positivo simétrico . Hubo muchos trabajos para intentar diseñar un método multirred robusto y rápido para problemas tan singulares. Se ha proporcionado una guía general como principio de diseño para lograr parámetros (por ejemplo, tamaño de malla y parámetros físicos como la relación de Poisson que aparecen en el operador casi singular) tasa de convergencia independiente del método multired aplicado a tales sistemas casi singulares, ^[24] es decir, en cada cuadrícula, se debe construir una descomposición espacial basada en la cual se aplica el suavizado, de modo que el espacio nulo de la parte singular del operador casi singular debe incluirse en la suma de los espacios nulos locales, la intersección del espacio nulo y los espacios locales resultantes de las descomposiciones espaciales. $A+\varepsilon M$ $\varepsilon$ $A$ $M$

Notas

^ Wienands romanos; Wolfgang Joppich (2005). Análisis práctico de Fourier para métodos multigrid. Prensa CRC. pag. 17.ISBN 978-1-58488-492-7.
^ U. Trotenberg; CW Oosterlee; A. Schüller (2001). Multired. Prensa académica. ISBN 978-0-12-701070-0.
^ Yu Zhu; Andreas C. Cangellaris (2006). Métodos de elementos finitos multired para el modelado de campos electromagnéticos. Wiley. pag. 132 y sigs . ISBN 978-0-471-74110-7.
^ Shah, Tasneem Mohammad (1989). Análisis del método multigrid (Tesis). Universidad de Oxford. Código bibliográfico : 1989STIN...9123418S.
^ MT Heath (2002). "Sección 11.5.7 Métodos multired". Computación científica: una encuesta introductoria . Educación superior McGraw-Hill. pag. 478 y sigs . ISBN 978-0-07-112229-0.
^ P. Wesseling (1992). Introducción a los métodos multired. Wiley. ISBN 978-0-471-93083-9.
^ Andrés V. Knyazev, Klaus Neymeyr. Solución eficiente de problemas de valores propios simétricos utilizando precondicionadores de redes múltiples en el método de gradiente conjugado de bloques localmente óptimo. Transacciones electrónicas sobre análisis numérico, 15, 38–55, 2003.
^ Bouwmeester, Henricus; Dougherty, Andrés; Knyazev, Andrés V. (2015). "Precondicionamiento no simétrico para métodos 1 de gradiente conjugado y descenso más pronunciado". Procedia Ciencias de la Computación . 51 : 276–285. arXiv : 1212.6680 . doi : 10.1016/j.procs.2015.05.241 . S2CID 51978658.
^ Xu, Jinchao. Teoría de los métodos multinivel. vol. 8924558. Ithaca, Nueva York: Universidad de Cornell, 1989.
^ Bramble, James H., Joseph E. Pasciak y Jinchao Xu. "Precondicionadores multinivel paralelos". Matemáticas de la Computación 55, no. 191 (1990): 1–22.
^ Xu, Jinchao. "Métodos iterativos por descomposición espacial y corrección subespacial". Revisión SIAM 34, núm. 4 (1992): 581-613.
^ F. Hülsemann; M. Kowarschik; el señor Mohr; U. Rüde (2006). "Multirrejilla geométrica paralela". En Son Magnus Bruaset; Aslak Tveito (eds.). Solución numérica de ecuaciones diferenciales parciales en computadoras paralelas . Birkhäuser. pag. 165.ISBN 978-3-540-29076-6.
^ Por ejemplo, J. Blaz̆ek (2001). Dinámica de fluidos computacional: principios y aplicaciones. Elsevier. pag. 305.ISBN 978-0-08-043009-6.y Achi Brandt y Rima Gandlin (2003). "Multired para la asimilación de datos atmosféricos: análisis". En Thomas Y. Hou; Eitan Tadmor (eds.). Problemas hiperbólicos: teoría, numérica, aplicaciones: actas de la Novena Conferencia Internacional sobre Problemas Hiperbólicos de 2002 . Saltador. pag. 369.ISBN 978-3-540-44333-9.
^ Achi Brandt (2002). "Computación científica multiescala: revisión". En Timothy J. Barth; Tony Chan; Robert Haimes (eds.). Métodos multiescala y multiresolución: teoría y aplicaciones . Saltador. pag. 53.ISBN 978-3-540-42420-8.
^ Björn Engquist; Olof Runborg (2002). "Homogeneización numérica basada en wavelets con aplicaciones". En Timothy J. Barth; Tony Chan; Robert Haimes (eds.). Métodos multiescala y multiresolución . vol. 20 de Apuntes de conferencias en ingeniería y ciencias computacionales. Saltador. pag. 140 y sigs . ISBN 978-3-540-42420-8.
^ U. Trotenberg; CW Oosterlee; A. Schüller (2001). Multired. ISBN 978-0-12-701070-0.
^ Albert Cohen (2003). Análisis numérico de métodos Wavelet. Elsevier. pag. 44.ISBN 978-0-444-51124-9.
^ U. Trotenberg; CW Oosterlee; A. Schüller (2001). "Capítulo 9: Multired adaptativa". Multired . pag. 356.ISBN 978-0-12-701070-0.
^ Yair Shapira (2003). "Multired algebraica". Multired basada en matrices: teoría y aplicaciones . Saltador. pag. 66.ISBN 978-1-4020-7485-1.
^ U. Trotenberg; CW Oosterlee; A. Schüller (2001). Multired. pag. 417.ISBN 978-0-12-701070-0.
^ Xu, J. y Zikatanov, L., 2017. Métodos algebraicos de redes múltiples. Acta Numérica, 26, págs.591-721. [1]
^ Hackbusch, Wolfgang (1985). "Métodos parabólicos de redes múltiples". Métodos informáticos en ciencias aplicadas e ingeniería, VI : 189–197. ISBN 9780444875976. Consultado el 1 de agosto de 2015 .
^ Horton, Graham (1992). "El método multigrid en tiempo paralelo". Comunicaciones en Métodos Numéricos Aplicados . 8 (9): 585–595. doi :10.1002/cnm.1630080906.
^ Young-Ju Lee, Jinbiao Wu, Jinchao Xu y Ludmil Zikatanov, Métodos robustos de corrección subespacial para sistemas casi singulares, modelos matemáticos y métodos en ciencias aplicadas, vol. 17, n.º 11, págs. 1937-1963 (2007)

Referencias

GP Astrachancev (1971), Un método iterativo para resolver problemas de redes elípticas. Comp. URSS. Matemáticas. Matemáticas. Física. 11, 171–182.
NS Bakhvalov (1966), Sobre la convergencia de un método de relajación con restricciones naturales del operador elíptico. Comp. URSS. Matemáticas. Matemáticas. Física. 6, 101-13.
Achi Brandt (abril de 1977), "Soluciones adaptativas multinivel para problemas de valores en la frontera", Matemáticas de la Computación , 31 : 333–90.
William L. Briggs, Van Emden Henson y Steve F. McCormick (2000), Un tutorial de redes múltiples (2ª ed.), Filadelfia: Sociedad de Matemáticas Industriales y Aplicadas , ISBN 0-89871-462-1 .
RP Fedorenko (1961), Un método de relajación para resolver ecuaciones en diferencias elípticas. Computación de la URSS. Matemáticas. Matemáticas. Física. 1, pág. 1092.
RP Fedorenko (1964), La velocidad de convergencia de un proceso iterativo. Computación de la URSS. Matemáticas. Matemáticas. Física. 4, pág. 227.
Prensa, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Sección 20.6. Métodos multicuadrícula para problemas de valores en la frontera". Recetas numéricas: el arte de la informática científica (3ª ed.). Nueva York: Cambridge University Press. ISBN 978-0-521-88068-8.

enlaces externos

Repositorio de métodos multicuadrícula, multinivel, multiescala, agregación, corrección de defectos y descomposición de dominios
Tutorial multirrejilla
Tutorial algebraico multigrid
Enlaces a presentaciones de AMG