Einstein sólido

Modelo de un sólido cristalino.

El sólido de Einstein es un modelo de sólido cristalino que contiene una gran cantidad de osciladores armónicos cuánticos tridimensionales independientes de la misma frecuencia. El supuesto de independencia se relaja en el modelo de Debye .

Si bien el modelo proporciona una concordancia cualitativa con los datos experimentales, especialmente para el límite de alta temperatura, estas oscilaciones son en realidad fonones , o modos colectivos que involucran a muchos átomos. Albert Einstein era consciente de que sería difícil obtener la frecuencia de las oscilaciones reales, pero aun así propuso esta teoría porque era una demostración particularmente clara de que la mecánica cuántica podía resolver el problema del calor específico en la mecánica clásica. ^[1]

Impacto histórico

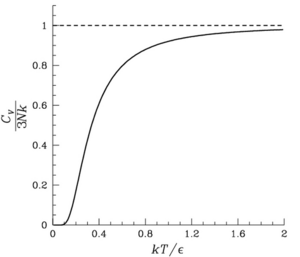
La teoría original propuesta por Einstein en 1907 tiene una gran relevancia histórica. La mecánica clásica requería la capacidad calorífica de los sólidos predicha por la ley empírica de Dulong-Petit ; el calor específico de los sólidos debería ser independiente de la temperatura. Pero los experimentos a bajas temperaturas demostraron que la capacidad calorífica cambia y llega a cero en el cero absoluto. A medida que aumenta la temperatura, el calor específico aumenta hasta acercarse a la predicción de Dulong y Petit a temperatura alta.

Al emplear el supuesto de cuantificación de Planck , la teoría de Einstein tuvo en cuenta por primera vez la tendencia experimental observada. Junto con el efecto fotoeléctrico , esto se convirtió en una de las pruebas más importantes de la necesidad de la cuantificación. Einstein utilizó los niveles del oscilador de la mecánica cuántica muchos años antes del advenimiento de la mecánica cuántica moderna .

Capacidad calorífica

Para un enfoque termodinámico, la capacidad calorífica se puede derivar utilizando diferentes conjuntos estadísticos . Todas las soluciones son equivalentes en el límite termodinámico .

Conjunto microcanónico

Capacidad calorífica de un sólido de Einstein en función de la temperatura. El valor experimental de 3 Nk se recupera a altas temperaturas.

La capacidad calorífica de un objeto a volumen constante V se define a través de la energía interna U como

${\displaystyle C_{V}=\left({\partial U \over \partial T}\right)_{V}.}$

${\displaystyle T}$, la temperatura del sistema, se puede encontrar a partir de la entropía

${\displaystyle {1 \over T}={\partial S \over \partial U}.}$

Para encontrar la entropía, considere un sólido formado por átomos, cada uno de los cuales tiene 3 grados de libertad. Entonces existen osciladores armónicos cuánticos (en adelante SHO para "osciladores armónicos simples"). ${\displaystyle N}$ ${\displaystyle 3N}$

${\displaystyle N^{\prime }=3N}$

Las posibles energías de un SHO están dadas por

${\displaystyle E_{n}=\hbar \omega \left(n+{1 \over 2}\right)}$

donde la n de SHO generalmente se interpreta como el estado de excitación de la masa oscilante, pero aquí n generalmente se interpreta como el número de fonones (bosones) que ocupan ese modo vibratorio (frecuencia). El efecto neto es que los niveles de energía están espaciados uniformemente y se puede definir un cuanto de energía debido a un fonón como

${\displaystyle \varepsilon =\hbar \omega }$

que es la cantidad más pequeña y única en la que aumenta la energía de un SHO. A continuación, debemos calcular la multiplicidad del sistema. Es decir, calcule el número de formas de distribuir cuantos de energía entre los SHO. Esta tarea se vuelve más sencilla si se piensa en distribuir piedras sobre cajas. ${\displaystyle q}$ ${\displaystyle N^{\prime }}$ ${\displaystyle q}$ ${\displaystyle N^{\prime }}$

o separar pilas de guijarros con tabiques ${\displaystyle N^{\prime }-1}$

o disponer guijarros y tabiques ${\displaystyle q}$ ${\displaystyle N^{\prime }-1}$

La última imagen es la más reveladora. El número de disposiciones de  objetos es . Entonces, el número de posibles disposiciones de guijarros y tabiques es . Sin embargo, si la partición 3 y la partición 5 se intercambian, nadie se daría cuenta. El mismo argumento se aplica a los cuantos. Para obtener el número de posibles arreglos distinguibles hay que dividir el número total de arreglos por el número de arreglos indistinguibles . Hay disposiciones de cuantos idénticas y disposiciones de partición idénticas. Por lo tanto, la multiplicidad del sistema viene dada por ${\displaystyle n}$ ${\displaystyle n!}$ ${\displaystyle q}$ ${\displaystyle N^{\prime }-1}$ ${\displaystyle \left(q+N^{\prime }-1\right)!}$ ${\displaystyle q!}$ ${\displaystyle (N^{\prime }-1)!}$

${\displaystyle \Omega ={\left(q+N^{\prime }-1\right)! \over q!(N^{\prime }-1)!}}$

que, como se mencionó anteriormente, es el número de formas de depositar cuantos de energía en osciladores. La entropía del sistema tiene la forma. ${\displaystyle q}$ ${\displaystyle N^{\prime }}$

${\displaystyle S/k=\ln \Omega =\ln {\left(q+N^{\prime }-1\right)! \over q!(N^{\prime }-1)!}.}$

${\displaystyle N^{\prime }}$es un número enorme; restarle uno no tiene ningún efecto general:

${\displaystyle S/k\approx \ln {\left(q+N^{\prime }\right)! \over q!N^{\prime }!}}$

Con la ayuda de la aproximación de Stirling , la entropía se puede simplificar:

${\displaystyle S/k\approx \left(q+N^{\prime }\right)\ln \left(q+N^{\prime }\right)-N^{\prime }\ln N^{\prime }-q\ln q.}$

La energía total del sólido está dada por

${\displaystyle U={N^{\prime }\varepsilon \over 2}+q\varepsilon ,}$

ya que hay q cuantos de energía en total en el sistema además de la energía del estado fundamental de cada oscilador. Algunos autores, como Schroeder, omiten esta energía del estado fundamental en su definición de energía total de un sólido de Einstein.

Ahora estamos listos para calcular la temperatura.

${\displaystyle {1 \over T}={\partial S \over \partial U}={\partial S \over \partial q}{dq \over dU}={1 \over \varepsilon }{\partial S \over \partial q}={k \over \varepsilon }\ln \left(1+N^{\prime }/q\right)}$

La eliminación de q entre las dos fórmulas anteriores da para U:

${\displaystyle U={N^{\prime }\varepsilon \over 2}+{N^{\prime }\varepsilon \over e^{\varepsilon /kT}-1}.}$

El primer término está asociado con la energía de punto cero y no contribuye al calor específico. Por lo tanto, se perderá en el siguiente paso.

Derivando con respecto a la temperatura para encontrar obtenemos: ${\displaystyle C_{V}}$

${\displaystyle C_{V}={\partial U \over \partial T}={N^{\prime }\varepsilon ^{2} \over kT^{2}}{e^{\varepsilon /kT} \over \left(e^{\varepsilon /kT}-1\right)^{2}}}$

o

${\displaystyle C_{V}=3Nk\left({\varepsilon \over kT}\right)^{2}{e^{\varepsilon /kT} \over \left(e^{\varepsilon /kT}-1\right)^{2}}.}$

Aunque el modelo de Einstein del sólido predice con precisión la capacidad calorífica a altas temperaturas, y en este límite

${\displaystyle \lim _{T\rightarrow \infty }C_{V}=3Nk}$, que equivale a la ley de Dulong-Petit , la capacidad calorífica se desvía notablemente de los valores experimentales a bajas temperaturas. Consulte el modelo de Debye para saber cómo calcular con precisión las capacidades caloríficas a baja temperatura.

conjunto canónico

La capacidad calorífica se obtiene mediante el uso de la función de partición canónica de un oscilador armónico cuántico simple.

${\displaystyle Z=\sum _{n=0}^{\infty }e^{-E_{n}/kT}}$

dónde

${\displaystyle E_{n}=\varepsilon \left(n+{1 \over 2}\right)}$

sustituyendo esto en la fórmula de la función de partición se obtiene

${\displaystyle {\begin{aligned}Z=\sum _{n=0}^{\infty }e^{-\varepsilon \left(n+1/2\right)/kT}=e^{-\varepsilon /2kT}\sum _{n=0}^{\infty }e^{-n\varepsilon /kT}=e^{-\varepsilon /2kT}\sum _{n=0}^{\infty }\left(e^{-\varepsilon /kT}\right)^{n}\\={e^{-\varepsilon /2kT} \over 1-e^{-\varepsilon /kT}}={1 \over e^{\varepsilon /2kT}-e^{-\varepsilon /2kT}}={1 \over 2\sinh \left({\varepsilon \over 2kT}\right)}.\end{aligned}}}$

Ésta es la función de partición de un oscilador armónico. Debido a que, estadísticamente, la capacidad calorífica, la energía y la entropía del sólido están distribuidas equitativamente entre sus átomos, podemos trabajar con esta función de partición para obtener esas cantidades y luego simplemente multiplicarlas por para obtener el total. A continuación, calculemos la energía promedio de cada oscilador. ${\displaystyle N^{\prime }}$

${\displaystyle \langle E\rangle =U=-{1 \over Z}\partial _{\beta }Z}$

dónde

${\displaystyle \beta ={1 \over kT}.}$

Por lo tanto,

${\displaystyle U=-2\sinh \left({\varepsilon \over 2kT}\right){-\cosh \left({\varepsilon \over 2kT}\right) \over 2\sinh ^{2}\left({\varepsilon \over 2kT}\right)}{\varepsilon \over 2}={\varepsilon \over 2}\coth \left({\varepsilon \over 2kT}\right).}$

La capacidad calorífica de un oscilador es entonces

${\displaystyle c_{V}={\partial U \over \partial T}=-{\varepsilon \over 2}{1 \over \sinh ^{2}\left({\varepsilon \over 2kT}\right)}\left(-{\varepsilon \over 2kT^{2}}\right)=k\left({\varepsilon \over 2kT}\right)^{2}{1 \over \sinh ^{2}\left({\varepsilon \over 2kT}\right)}.}$

Hasta ahora hemos calculado la capacidad calorífica de un grado de libertad único, que ha sido modelado como un armónico cuántico. La capacidad calorífica de todo el sólido viene dada por , donde el número total de grados de libertad del sólido es tres veces (para los tres grados de libertad direccionales) , el número de átomos en el sólido. Se obtiene así ${\displaystyle C_{V}=3Nc_{V}}$ ${\displaystyle N}$

${\displaystyle C_{V}=3Nk\left({\varepsilon \over 2kT}\right)^{2}{1 \over \sinh ^{2}\left({\varepsilon \over 2kT}\right)}.}$

que es algebraicamente idéntica a la fórmula derivada en la sección anterior.

La cantidad tiene las dimensiones de la temperatura y es una propiedad característica de un cristal. Se la conoce como temperatura de Einstein . ^[2] Por lo tanto, el modelo cristalino de Einstein predice que la energía y las capacidades caloríficas de un cristal son funciones universales de la relación adimensional . De manera similar, el modelo de Debye predice una función universal de la relación , donde es la temperatura de Debye. ${\displaystyle T_{\rm {E}}=\varepsilon /k}$ ${\displaystyle T/T_{\rm {E}}}$ ${\displaystyle T/T_{\rm {D}}}$ ${\displaystyle T_{\rm {D}}}$

Limitaciones y modelo sucesor

En el modelo de Einstein, el calor específico se acerca a cero exponencialmente rápido a bajas temperaturas. Esto se debe a que todas las oscilaciones tienen una frecuencia común. El comportamiento correcto se encuentra cuantizando los modos normales del sólido de la misma forma que sugirió Einstein. Entonces las frecuencias de las ondas no son todas iguales y el calor específico llega a cero como ley de potencia, lo que coincide con el experimento. Esta modificación se llama modelo Debye , que apareció en 1912. ${\displaystyle T^{3}}$

Ver también

• Teoría cinética de los sólidos.

Referencias

1. Mandl, F. (1988) [1971]. Física estadística (2ª ed.). Chichester·Nueva York·Brisbane·Toronto·Singapur: John Wiley & Sons . ISBN 978-0471915331.
2. Rogers, Donald (2005). La otra teoría de Einstein: la teoría de la capacidad calorífica de Planck-Bose-Einstein . Prensa de la Universidad de Princeton. pag. 73.ISBN​ 0-691-11826-4.

enlaces externos

• Zeleny, Enrique. "El proyecto de demostraciones de Wolfram - Einstein Solid" . Consultado el 18 de marzo de 2016 ..