Mezcla caótica

Un ejemplo de mezcla caótica

En la teoría del caos y la dinámica de fluidos , la mezcla caótica es un proceso por el cual los trazadores de flujo se transforman en fractales complejos bajo la acción de un flujo de fluido . El flujo se caracteriza por un crecimiento exponencial de los filamentos de fluido. ^{[1] [2]} Incluso flujos muy simples, como el vórtice parpadeante o los campos de viento de resolución finita pueden generar patrones excepcionalmente complejos a partir de campos trazadores inicialmente simples. ^[3]

El fenómeno aún no se comprende bien y es objeto de mucha investigación actual.

Contexto de advección caótica

Flujos de fluidos

Dos mecanismos básicos son responsables de la mezcla de fluidos : difusión y advección . En los líquidos , la difusión molecular por sí sola no es eficiente para la mezcla. La advección, es decir, el transporte de materia mediante un flujo, es necesaria para una mejor mezcla.

El flujo de fluido obedece a ecuaciones fundamentales de la dinámica de fluidos (como la conservación de la masa y la conservación del momento) llamadas ecuaciones de Navier-Stokes . Estas ecuaciones están escritas para el campo de velocidad euleriano en lugar de para la posición lagrangiana de las partículas del fluido. Las trayectorias lagrangianas se obtienen integrando el flujo. Estudiar el efecto de la convección en la mezcla de fluidos equivale a describir cómo diferentes partículas lagrangianas de fluido exploran el dominio del fluido y se separan entre sí.

Condiciones para la advección caótica

Un flujo de fluido puede considerarse como un sistema dinámico, es decir, un conjunto de ecuaciones diferenciales ordinarias que determinan la evolución de una trayectoria lagrangiana . Estas ecuaciones se denominan ecuaciones de advección :

${\displaystyle {\frac {d{\vec {x}}}{dt}}={\vec {v}}({\vec {x}},t)}$

donde son los componentes del campo de velocidad, que se supone que se conocen a partir de la solución de las ecuaciones que gobiernan el flujo de fluidos, como las ecuaciones de Navier-Stokes , y es la posición física. Si el sistema dinámico que gobierna las trayectorias es caótico , la integración de una trayectoria es extremadamente sensible a las condiciones iniciales y los puntos vecinos se separan exponencialmente con el tiempo. Este fenómeno se llama advección caótica . ${\displaystyle {\vec {v}}=(u,v,w)}$ ${\displaystyle {\vec {x}}=(x,y,z)}$

Los sistemas dinámicos y la teoría del caos establecen que se necesitan al menos 3 grados de libertad para que un sistema dinámico sea caótico. Los flujos tridimensionales tienen tres grados de libertad correspondientes a las tres coordenadas y, por lo general, dan lugar a una advección caótica, excepto cuando el flujo tiene simetrías que reducen el número de grados de libertad. En flujos con menos de 3 grados de libertad, las trayectorias lagrangianas se limitan a tubos cerrados y la mezcla inducida por cizallamiento solo puede tener lugar dentro de estos tubos.

Este es el caso de los flujos estacionarios en 2-D en los que solo hay dos grados de libertad y . Para flujos estacionarios (independientes del tiempo), las trayectorias lagrangianas de las partículas de fluido coinciden con las líneas de corriente del flujo, que son isolíneas de la función de corriente . En 2-D, las líneas de corriente son curvas cerradas concéntricas que se cruzan solo en puntos de estancamiento . Por lo tanto, una mancha de fluido teñido que se va a mezclar solo puede explorar la región limitada por la línea de corriente más externa e interna, sobre la que se encuentra en el tiempo inicial. En cuanto a las aplicaciones prácticas, esta configuración no es muy satisfactoria. ${\displaystyle x}$ ${\displaystyle y}$

Para flujos no estacionarios (dependientes del tiempo) en 2-D , las líneas de corriente cerradas instantáneas y las trayectorias lagrangianas ya no coinciden. Por lo tanto, las trayectorias lagrangianas exploran un volumen mayor del volumen, lo que resulta en una mejor mezcla. La advección caótica se observa para la mayoría de los flujos no estacionarios en 2-D. Un ejemplo famoso es el flujo de vórtice parpadeante introducido por Aref, ^[4] donde dos agitadores fijos en forma de varilla giran alternativamente dentro del fluido. Cambiar periódicamente el agitador activo (rotativo) introduce una dependencia del tiempo en el flujo, lo que resulta en una advección caótica. Por lo tanto, las trayectorias lagrangianas pueden escapar de las líneas de corriente cerradas y visitar una gran fracción del dominio del fluido.

Cortar

Un flujo promueve la mezcla al separar las partículas de fluido vecinas. Esta separación se produce debido a gradientes de velocidad , un fenómeno llamado cizallamiento . Sean y dos partículas de fluido vecinas, separadas por en el tiempo t . Cuando las partículas son transportadas por un flujo , en el tiempo la separación aproximada entre las partículas se puede encontrar a través de la expansión de Taylor  : ${\displaystyle {\vec {x}}_{1}}$ ${\displaystyle {\vec {x}}_{2}}$ ${\displaystyle \delta {\vec {x}}={\vec {x}}_{2}-{\vec {x}}_{1}}$ ${\displaystyle {\vec {v}}}$ ${\displaystyle t+\delta t}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}({\vec {x}}+\delta {\vec {x}})\approx {\vec {v}}+\nabla {\vec {v}}\cdot \delta {\vec {x}}}$

por eso

${\displaystyle \delta x(t+\delta t)\approx \delta x(t)+\delta t(\delta x\cdot \nabla ){\vec {v}}}$

y

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\delta {\vec {x}}\approx \nabla {\vec {v}}\cdot \delta {\vec {x}}}$

Por lo tanto, la tasa de crecimiento de la separación viene dada por el gradiente del campo de velocidad en la dirección de la separación. El flujo de cizallamiento plano es un ejemplo simple de flujo estacionario a gran escala que deforma los elementos del fluido debido a un cizallamiento uniforme.

Caracterización de la advección caótica

Exponentes de Lyapunov

Si el flujo es caótico , entonces los pequeños errores iniciales, , en una trayectoria divergirán exponencialmente. Nos interesa calcular la estabilidad, es decir, ¿qué tan rápido divergen las trayectorias cercanas? La matriz de Jacobi del campo de velocidad, , proporciona información sobre la tasa local de divergencia de las trayectorias cercanas o la tasa local de estiramiento del espacio de Lagrange . ${\displaystyle \delta {\vec {x}}}$ ${\displaystyle \nabla {\vec {v}}}$

Definimos la matriz H tal que:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\boldsymbol {H}}\equiv \nabla {\vec {v}}\cdot {\boldsymbol {H}},\qquad {\boldsymbol {H}}(t=0)={\boldsymbol {I}}}$

donde I es la matriz identidad. De ello se deduce que:

${\displaystyle \delta {\vec {x}}(t)\approx {\boldsymbol {H}}\cdot \delta {\vec {x}}_{0}}$

Los exponentes de Lyapunov de tiempo finito se definen como el promedio temporal de los logaritmos de las longitudes de los componentes principales del vector H durante un tiempo t:

${\displaystyle {\boldsymbol {H^{T}}}\cdot {\boldsymbol {H}}\cdot \delta {\vec {x}}_{0i}=h_{i}\cdot \delta {\vec {x}}_{0i}}$

${\displaystyle \lambda _{i}({\vec {x}},t)\equiv {\frac {1}{2t}}\ln {h_{i}({\vec {x}},t)}}$

donde es el i- ésimo exponente de Lyapunov del sistema, mientras que es el i -ésimo componente principal de la matriz H . ${\displaystyle \lambda _{i}({\vec {x}},t)\geq \lambda _{i+1}({\vec {x}},t)}$ ${\displaystyle \delta {\vec {x}}_{0i}}$

Si comenzamos con un conjunto de vectores de error iniciales ortonormales, entonces la matriz H los mapeará a un conjunto de vectores de error ortogonales finales de longitud . La acción del sistema mapea una esfera infinitesimal de puntos iniciales a un elipsoide cuyo eje mayor está dado por mientras que el eje menor está dado por , donde N es el número de dimensiones. ^{[5] [6]} ${\displaystyle \{\delta {\vec {x}}_{0i}\}}$ ${\displaystyle \left\{{\sqrt {h_{i}({\vec {x}},t)}}\right\}}$ ${\displaystyle {\sqrt {h_{1}({\vec {x}},t)}}}$ ${\displaystyle {\sqrt {h_{N}({\vec {x}},t)}}}$

Esta definición de exponentes de Lyapunov es más elegante y más apropiada para sistemas dinámicos de tiempo continuo del mundo real que la definición más habitual basada en funciones discretas. El caos se define como la existencia de al menos un exponente de Lyapunov positivo.

En un sistema caótico , llamamos exponente de Lyapunov al valor asintótico del mayor valor propio de H :

${\displaystyle \lambda =\lim _{t\to \infty }\lambda _{1}({\vec {x}},t).}$

Si existe alguna diferencia significativa entre los exponentes de Lyapunov, a medida que un vector de error evoluciona hacia adelante en el tiempo, cualquier desplazamiento en la dirección de mayor crecimiento tenderá a magnificarse. Por lo tanto:

${\displaystyle |\delta {\vec {x}}|\approx |\delta {\vec {x}}_{0}|e^{\lambda _{1}t}.}$

El exponente de Lyapunov de un flujo es una cantidad única que caracteriza la separación asintótica de las partículas de fluido en un flujo determinado. Se utiliza a menudo como medida de la eficiencia de la mezcla, ya que mide la velocidad con la que las trayectorias se separan entre sí debido a la advección caótica. El exponente de Lyapunov se puede calcular mediante diferentes métodos:

• siguiendo una única trayectoria durante tiempos muy largos y calculando . ${\displaystyle \lambda =\lim _{t\to \infty }\lambda _{1}({\vec {x}},t)}$
• o siguiendo un conjunto de trayectorias durante un período de tiempo determinado y calculando el promedio del conjunto: . ${\displaystyle <\lambda >_{\mathrm {trajectories} }}$

La equivalencia de los dos métodos se debe a la ergodicidad del sistema caótico.

Crecimiento del filamento versus evolución del gradiente trazador

La siguiente ecuación exacta se puede derivar de una ecuación de advección-difusión (ver más abajo), con un término de difusión ( D=0 ) de cero:

${\displaystyle {\frac {\mathrm {d} \nabla q}{\mathrm {d} t}}=-\nabla q\cdot \nabla {\vec {v}}}$

Paralelamente a la definición del exponente de Lyapunov, definimos la matriz , de la siguiente manera: ${\displaystyle {\boldsymbol {H}}^{\prime }}$

${\displaystyle {\frac {\mathrm {d} {\boldsymbol {H^{\prime }}}}{\mathrm {d} t}}=-\nabla {\boldsymbol {H^{\prime }}}\cdot \nabla {\vec {v}}\qquad {\boldsymbol {H^{\prime }}}(t=0)={\boldsymbol {I}}}$

Es fácil demostrar que:

${\displaystyle {\boldsymbol {H^{\prime }}}={\boldsymbol {H}}^{-1}}$

Si definimos como las longitudes al cuadrado de los componentes principales de la matriz de gradiente del trazador, , entonces: ${\displaystyle \lbrace h_{i}^{\prime }\rbrace }$ ${\displaystyle {\boldsymbol {H}}^{\prime }}$

${\displaystyle h_{i}^{\prime }=1/h_{i}}$

donde los s están ordenados, como antes, de mayor a menor. Por lo tanto, el crecimiento en el vector de error causará una disminución correspondiente en el gradiente del trazador y viceversa. Esto se puede entender de manera muy simple e intuitiva considerando dos puntos cercanos: dado que la diferencia en la concentración del trazador será fija, la única fuente de variación en los gradientes entre ellos será su separación. ^{[5] [7]} ${\displaystyle \lbrace h_{i}^{\prime }\rbrace }$

Advección de contorno

Evolución de un contorno advectivo

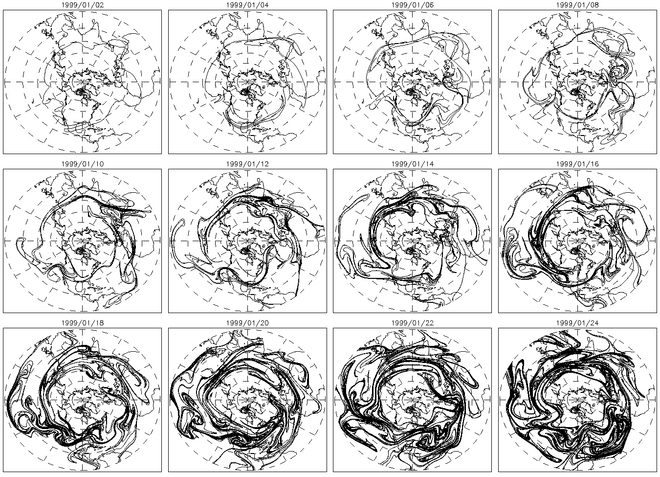
La advección de contornos es otro método útil para caracterizar la mezcla caótica. En los flujos caóticos, los contornos advectos crecerán exponencialmente con el tiempo. La figura anterior muestra la evolución cuadro por cuadro de un contorno advecto a lo largo de varios días. La figura de la derecha muestra la longitud de este contorno en función del tiempo.

Crecimiento del contorno advectivo

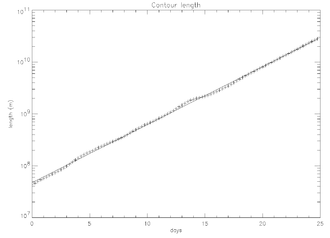
Es fácil ver el vínculo entre el crecimiento exponencial del contorno y los exponentes positivos de Lyapunov. La tasa de crecimiento del contorno se expresa como:

${\displaystyle {\frac {\mathrm {d} L}{\mathrm {d} t}}=\int |\nabla {\vec {v}}\cdot \mathrm {d} {\vec {s}}|}$

donde es la trayectoria y la integral se realiza a lo largo del contorno. Las tasas de crecimiento del contorno se aproximarán al promedio de los grandes exponentes de Lyapunov: ^[5] ${\displaystyle \mathrm {d} {\vec {s}}}$

${\displaystyle L\approx L_{0}\exp({\bar {\lambda }}_{1}t)}$

Secciones de Poincaré

En la advección caótica, una partícula de fluido se desplaza dentro de una gran región y se encuentra con otras partículas que inicialmente estaban lejos de ella. Se puede considerar entonces que una partícula se mezcla con partículas que se desplazan dentro de la misma región. Sin embargo, la región cubierta por una trayectoria no siempre abarca todo el dominio del fluido. Las secciones de Poincaré se utilizan para distinguir las regiones de buena y mala mezcla.

El mapa de Poincaré se define como la transformación

${\displaystyle {\begin{aligned}{\boldsymbol {M}}\colon {\vec {x_{i}}}(t_{i})&\to {\vec {x}}_{i+1}(t_{i+1}=t_{i}+T,{\vec {x_{i}}}).\end{aligned}}}$

${\displaystyle {\boldsymbol {M}}}$transforma una partícula puntual en la posición de la partícula después de un intervalo de tiempo T. En particular, para un flujo periódico en el tiempo con período T, al aplicar la función varias veces a una partícula se obtienen las posiciones sucesivas de la partícula período tras período. Una sección de Poincaré se construye partiendo de unas pocas condiciones iniciales diferentes y trazando las iteraciones correspondientes. Esto se reduce a trazar las trayectorias estroboscópicas cada T.

Como ejemplo, la figura que se presenta aquí (parte izquierda) representa la sección de Poincaré que se obtiene al aplicar periódicamente un movimiento en forma de ocho a una varilla mezcladora circular. Algunas trayectorias abarcan una gran región: ésta es la región caótica o de mezcla, donde se produce una buena mezcla. Sin embargo, también hay dos "agujeros": en estas regiones, las trayectorias están cerradas. Se denominan islas elípticas, ya que las trayectorias en su interior son curvas de tipo elíptico. Estas regiones no se mezclan con el resto del fluido. Para aplicaciones de mezcla, las islas elípticas deben evitarse por dos razones:

• Las partículas fluidas no pueden cruzar los límites de las islas (excepto por difusión lenta), lo que produce segregación.
• La mezcla dentro de estas regiones no es eficiente porque las trayectorias están cerradas y, por lo tanto, no son caóticas.

Para evitar la formación de islas no caóticas es necesario comprender el origen físico de estas regiones. En términos generales, cambiar la geometría del flujo puede modificar la presencia o ausencia de islas. En el flujo en forma de ocho, por ejemplo, en el caso de una varilla muy delgada, la influencia de la varilla no se siente lejos de su ubicación y existen trayectorias casi circulares dentro de los bucles de la figura en forma de ocho. Con una varilla más grande (parte derecha de la figura), las partículas pueden escapar de estos bucles y las islas ya no existen, lo que da como resultado una mejor mezcla.

Con una sección de Poincaré, la calidad de la mezcla de un flujo se puede analizar distinguiendo entre regiones caóticas y elípticas. Sin embargo, esta es una medida rudimentaria del proceso de mezcla, ya que las propiedades de estiramiento no se pueden inferir a partir de este método de mapeo. No obstante, esta técnica es muy útil para estudiar la mezcla de flujos periódicos y se puede extender a un dominio 3D.

Dimensión fractal

A través de un proceso continuo de estiramiento y plegado, muy similar a un " mapa del panadero ", los trazadores advectos en flujos caóticos se convertirán en fractales complejos. La dimensión fractal de un solo contorno estará entre 1 y 2. El crecimiento exponencial garantiza que el contorno, en el límite de la integración temporal muy larga, se vuelva fractal. Los fractales compuestos por una sola curva son infinitamente largos y, cuando se forman iterativamente, tienen una tasa de crecimiento exponencial, al igual que un contorno advecto. El copo de nieve de Koch , por ejemplo, crece a una tasa de 4/3 por iteración.

La figura siguiente muestra la dimensión fractal de un contorno advectivo en función del tiempo, medida de cuatro maneras diferentes. Un buen método para medir la dimensión fractal de un contorno advectivo es el exponente de incertidumbre .

Dimensión fractal del contorno advectivo ^[5]

Evolución de los campos de concentración de trazadores en advección caótica

En la mezcla de fluidos, a menudo se desea homogeneizar una especie, que puede caracterizarse por su campo de concentración q . A menudo, la especie puede considerarse como un trazador pasivo que no modifica el flujo. La especie puede ser, por ejemplo, un tinte que se va a mezclar. La evolución de un campo de concentración obedece a la ecuación de advección-difusión , también llamada ecuación de convección-difusión : ${\displaystyle q}$

${\displaystyle {\big .}{\frac {\partial q}{\partial t}}=\nabla \cdot D\nabla q-{\vec {v}}\cdot \nabla q.}$

En comparación con la ecuación de difusión simple, el término proporcional al campo de velocidad representa el efecto de la advección. ${\displaystyle {\vec {v}}}$

Al mezclar una mancha de trazador, el término de advección domina la evolución del campo de concentración al comienzo del proceso de mezcla. La advección caótica transforma la mancha en un haz de filamentos finos. El ancho de un filamento de colorante disminuye exponencialmente con el tiempo, hasta que se alcanza una escala de equilibrio, en la que el efecto de la difusión comienza a ser significativo. Esta escala se llama escala de Batchelor . Se define como la raíz cuadrada de la relación entre el coeficiente de difusión y el exponente de Lyapunov.

${\displaystyle w_{B}={\sqrt {\frac {D}{\lambda }}}}$

donde es el exponente de Lyapunov y D es el coeficiente de difusión. Esta escala mide el equilibrio entre el estiramiento y la difusión en la evolución del campo de concentración: el estiramiento tiende a disminuir el ancho de un filamento, mientras que la difusión tiende a aumentarlo. La escala de Batchelor es la escala de longitud más pequeña que se puede observar en el campo de concentración, ya que la difusión difumina rápidamente cualquier detalle más fino. ${\displaystyle \lambda }$

Cuando la mayoría de los filamentos de colorante alcanzan la escala Batchelor, la difusión comienza a disminuir significativamente el contraste de concentración entre el filamento y el dominio circundante. Por lo tanto, el tiempo en el que un filamento alcanza la escala Batchelor se denomina tiempo de mezcla. La resolución de la ecuación de advección-difusión muestra que después del tiempo de mezcla de un filamento, la disminución de la fluctuación de concentración debido a la difusión es exponencial, lo que da como resultado una homogeneización rápida con el fluido circundante.

Historia de la advección caótica

El nacimiento de la teoría de la advección caótica se remonta generalmente a un artículo de 1984 ^[4] de Hassan Aref . En este trabajo, Aref estudió la mezcla inducida por dos vórtices que se activan y desactivan alternativamente dentro de un fluido no viscoso . Este trabajo seminal había sido posible gracias a desarrollos anteriores en los campos de los sistemas dinámicos y la mecánica de fluidos en las décadas anteriores. Vladimir Arnold ^[8] y Michel Hénon ^[9] ya habían notado que las trayectorias advectadas por flujos tridimensionales que preservan el área podían ser caóticas. Sin embargo, el interés práctico de la advección caótica para aplicaciones de mezcla de fluidos permaneció inadvertido hasta el trabajo de Aref en los años 80. Desde entonces, todo el conjunto de herramientas de sistemas dinámicos y teoría del caos se ha utilizado para caracterizar la mezcla de fluidos por advección caótica. ^[1] Trabajos recientes, por ejemplo, han empleado métodos topológicos para caracterizar el estiramiento de partículas de fluido. ^[10] Otras direcciones recientes de investigación se refieren al estudio de la advección caótica en flujos complejos, como los flujos granulares. ^[11]

Referencias

1. JM Ottino (1989). La cinemática de la mezcla: estiramiento, caos y transporte . Cambridge University Press .
2. Aref, Hassan; Blake, John R.; Budišić, Marko; Cardoso, Silvana SS; Cartwright, Julyan HE ; Clercx, Herman JH; El Omari, Kamal; Feudel, Ulrike; Golestanian, Ramin (14 de junio de 2017). "Fronteras de la advección caótica". Reseñas de Física Moderna . 89 (2): 025007. arXiv : 1403.2953 . Código Bibliográfico :2017RvMP...89b5007A. doi :10.1103/RevModPhys.89.025007. S2CID  117496075.
3. J. Methven y B. Hoskins (1999). "La advección de trazadores de alta resolución por vientos de baja resolución". Revista de Ciencias Atmosféricas . 56 (18): 3262–3285. Bibcode :1999JAtS...56.3262M. doi : 10.1175/1520-0469(1999)056<3262:taohrt>2.0.co;2 .
4. Aref, H. (junio de 1984). "Agitación por advección caótica". Journal of Fluid Mechanics . 143 : 1–21. Bibcode :1984JFM...143....1A. doi :10.1017/S0022112084001233. S2CID  122846084.
5. Peter Mills (2004). Siguiendo la estela de vapor: un estudio de la mezcla caótica del vapor de agua en la troposfera superior (PDF) (Tesis). Universidad de Bremen. Archivado desde el original (PDF) el 2011-07-21 . Consultado el 2010-12-16 .
6. Edward Ott (1993). Caos en sistemas dinámicos . Cambridge University Press.
7. Arjendu K. Pattanayak (2001). "Caracterización del equilibrio metaestable entre el caos y la difusión". Physica D . 148 (1–2): 1–19. Bibcode :2001PhyD..148....1P. doi :10.1016/S0167-2789(00)00186-X.
8. Arnold, Vladimir Igorevich (5 de julio de 1965). "Sur la topologie des écoulements stationnaires des fluides parfaits" [Sobre la topología de flujos estacionarios de fluidos ideales]. Comptes rendus hebdomadaires des séances de l'Académie des Sciences (en francés). 261 . Academia Francesa de Ciencias : 17-20. doi :10.1007/978-3-642-31031-7_3. ISBN 978-3-642-31030-0. ISSN  0001-4036.
9. Hénon, Michel (31 de enero de 1966). "Sur la topologie des lignes de courant dans un cas particulier" [Sobre la topología de líneas de corriente en un caso especial]. Comptes rendus hebdomadaires des séances de l'Académie des Sciences . A (en francés). 262 . Academia Francesa de Ciencias : 312–4. ISSN  0997-4482.
10. J.-L. Thiffeault y MD Finn (2006). "Topología, trenzas y mezcla en fluidos". Philosophical Transactions of the Royal Society A . 364 (1849): 3251–3266. arXiv : nlin/0603003 . Bibcode :2006RSPTA.364.3251T. doi :10.1098/rsta.2006.1899. PMID  17090458. S2CID  10401399.
11. JM Ottino y DV Khakhar (2000). "Mezcla y segregación de materiales granulares". Revista anual de mecánica de fluidos . 32 : 55–91. Código Bibliográfico :2000AnRFM..32...55O. doi :10.1146/annurev.fluid.32.1.55. S2CID  5862876.

Enlaces externos

• ctraj: Herramientas para estudiar la advección caótica.