Sumador (electrónica)

Circuito digital que produce sumas a partir de entradas

Un sumador , o sumador , ^[1] es un circuito digital que realiza la suma de números. En muchos ordenadores y otros tipos de procesadores , los sumadores se utilizan en las unidades aritmético-lógicas (ALU). También se utilizan en otras partes del procesador, donde se utilizan para calcular direcciones , índices de tablas , operadores de incremento y decremento y operaciones similares.

Aunque se pueden construir sumadores para muchas representaciones numéricas , como el decimal codificado en binario o el exceso de 3 , los sumadores más comunes operan con números binarios . En los casos en que se utiliza el complemento a dos o el complemento a uno para representar números negativos , es trivial modificar un sumador para convertirlo en un sumador-restador . Otras representaciones numéricas con signo requieren más lógica en torno al sumador básico.

Historia

George Stibitz inventó el sumador binario de 2 bits (el modelo K ) en 1937.

Sumadores binarios

Media sumadora

El semisumador suma dos dígitos binarios simples y . Tiene dos salidas, suma ( ) y acarreo ( ). La señal de acarreo representa un desbordamiento al siguiente dígito de una suma de varios dígitos. El valor de la suma es . El diseño de semisumador más simple, que se muestra a la derecha, incorpora una compuerta XOR para y una compuerta AND para . La lógica booleana para la suma (en este caso ) será mientras que para el acarreo ( ) será . Con la adición de una compuerta OR para combinar sus salidas de acarreo, dos semisumadores se pueden combinar para formar un sumador completo. ^[2] El semisumador suma dos bits de entrada y genera un acarreo y una suma, que son las dos salidas de un semisumador. Las variables de entrada de un semisumador se denominan bits de sumando y sumando. Las variables de salida son la suma y el acarreo. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle S}$ ${\displaystyle C}$ ${\displaystyle 2C+S}$ ${\displaystyle S}$ ${\displaystyle C}$ ${\displaystyle S}$ ${\displaystyle A\oplus B}$ ${\displaystyle C}$ ${\displaystyle A\cdot B}$

La tabla de verdad para el medio sumador es:

Varios circuitos lógicos digitales de medio sumador:

• 
  Media víbora en acción.
• 
  Esquema de medio sumador implementado con una puerta XOR y una puerta AND .
• 
  Esquema de medio sumador implementado con cinco puertas NAND .
• 
  Símbolo esquemático para un sumador de medio bit.

Sumador completo

Un sumador completo suma números binarios y tiene en cuenta los valores que entran y salen. Un sumador completo de un bit suma tres números de un bit, que suelen escribirse como , , y ; y son los operandos, y es un bit que entra desde la etapa anterior menos significativa. ^[3] El circuito produce una salida de dos bits. El acarreo y la suma de salida suelen estar representados por las señales y , donde la suma es igual a . El sumador completo suele ser un componente de una cascada de sumadores, que suman números binarios de 8, 16, 32, etc. bits. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C_{in}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C_{in}}$ ${\displaystyle C_{out}}$ ${\displaystyle S}$ ${\displaystyle 2C_{out}+S}$

Un sumador completo se puede implementar de muchas maneras diferentes, como con un circuito a nivel de transistor personalizado o compuesto por otras puertas. La implementación más común es con:

${\displaystyle S=A\oplus B\oplus C_{in}}$

${\displaystyle C_{out}=(A\cdot B)+(C_{in}\cdot (A\oplus B))}$

Las expresiones anteriores para y se pueden derivar del uso de un mapa de Karnaugh para simplificar la tabla de verdad. ${\displaystyle S}$ ${\displaystyle C_{in}}$

En esta implementación, la compuerta OR final antes de la salida de ejecución puede reemplazarse por una compuerta XOR sin alterar la lógica resultante. Esto se debe a que cuando A y B son ambos 1, el término siempre es 0 y, por lo tanto, solo puede ser 0. Por lo tanto, las entradas a la compuerta OR final nunca pueden ser ambas 1 (esta es la única combinación para la cual las salidas OR y XOR difieren). ${\displaystyle (A\oplus B)}$ ${\displaystyle (C_{in}\cdot (A\oplus B))}$

Debido a la propiedad de completitud funcional de las puertas NAND y NOR, también se puede implementar un sumador completo utilizando nueve puertas NAND , ^[4] o nueve puertas NOR .

Usar solo dos tipos de puertas es conveniente si el circuito se implementa utilizando chips de circuitos integrados simples que contienen solo un tipo de puerta por chip.

Un sumador completo también se puede construir a partir de dos semisumadores conectando y a la entrada de un semisumador, luego tomando su salida de suma como una de las entradas del segundo semisumador y como su otra entrada, y finalmente las salidas de acarreo de los dos semisumadores se conectan a una compuerta OR. La salida de suma del segundo semisumador es la salida de suma final ( ) del sumador completo y la salida de la compuerta OR es la salida de acarreo final ( ). La ruta crítica de un sumador completo pasa por ambas compuertas XOR y termina en el bit de suma . Suponiendo que una compuerta XOR tarda 1 retrasos en completarse, el retraso impuesto por la ruta crítica de un sumador completo es igual a: ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle S}$ ${\displaystyle C_{in}}$ ${\displaystyle S}$ ${\displaystyle C_{out}}$ ${\displaystyle S}$

${\displaystyle T_{\text{FA}}=2\cdot T_{\text{XOR}}=2D}$

La ruta crítica de un acarreo pasa por una puerta XOR en el sumador y por 2 puertas (AND y OR) en el bloque de acarreo y, por lo tanto, si las puertas AND u OR tardan 1 retraso en completarse, tienen un retraso de:

${\displaystyle T_{\text{c}}=T_{\text{XOR}}+T_{\text{AND}}+T_{\text{OR}}=D+D+D=3D}$

La tabla de verdad para el sumador completo es:

Al invertir todas las entradas de un sumador completo también se invierten todas sus salidas, lo que se puede utilizar en el diseño de sumadores rápidos con acarreo de ondulación, porque no hay necesidad de invertir el acarreo. ^[5]

Varios circuitos lógicos digitales sumadores completos:

• 
  Sumador completo en acción.
• 
  Esquema de un sumador completo implementado con dos puertas XOR , dos puertas AND y una puerta OR .
• 
  Esquema de un sumador completo implementado con nueve puertas NAND .
• 
  Esquema de un sumador completo implementado con nueve puertas NOR .
• 
  Sumador completo con salidas invertidas con retardo de propagación de acarreo de un solo transistor en CMOS ^[5]
• 
  Símbolo esquemático para un sumador completo de 1 bit con C _{de entrada} y C _{de salida} dibujados en los lados del bloque para enfatizar su uso en un sumador de múltiples bits

Sumadores que admiten varios bits

Sumador de acarreo de ondulación

Sumador de 4 bits con diagrama de bloques lógicos mostrado

Sumador de acarreo de ondulación decimal de 4 dígitos. FA = sumador completo, HA = medio sumador.

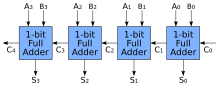
Es posible crear un circuito lógico utilizando múltiples sumadores completos para sumar números de N bits. Cada sumador completo ingresa un , que es el del sumador anterior. Este tipo de sumador se llama sumador de acarreo de ondulación (RCA), ya que cada bit de acarreo "ondula" al siguiente sumador completo. El primer (y solo el primero) sumador completo puede reemplazarse por un medio sumador (suponiendo que ). ${\displaystyle C_{in}}$ ${\displaystyle C_{out}}$ ${\displaystyle C_{in}=0}$

El diseño de un sumador de acarreo-ondulación es simple, lo que permite un tiempo de diseño rápido; sin embargo, el sumador de acarreo-ondulación es relativamente lento, ya que cada sumador completo debe esperar a que se calcule el bit de acarreo a partir del sumador completo anterior. El retardo de compuerta se puede calcular fácilmente mediante la inspección del circuito del sumador completo. Cada sumador completo requiere tres niveles de lógica. En un sumador de acarreo-ondulación de 32 bits, hay 32 sumadores completos, por lo que el retardo de la ruta crítica (peor caso) es 3 (desde la entrada hasta el acarreo en el primer sumador) + 31 × 2 (para la propagación del acarreo en los últimos sumadores) = 65 retardos de compuerta. ^[6] La ecuación general para el retardo en el peor caso para un sumador de acarreo-ondulación de n bits, que tiene en cuenta tanto los bits de suma como los de acarreo, es:

${\displaystyle T_{\text{CRA}}(n)=T_{\text{HA}}+(n-1)\cdot T_{\text{c}}+T_{\text{s}}=}$ ${\displaystyle T_{\text{FA}}+(n-1)\cdot T_{c}=}$ ${\displaystyle 3D+(n-1)\cdot 2D=(2n+1)\cdot D}$

Un diseño con polaridades de acarreo alternas y puertas AND-OR-Invert optimizadas puede ser aproximadamente el doble de rápido. ^{[7] [5]}

Sumador de acarreo y previsión (Weinberger y Smith, 1958)

Sumador de 4 bits con acarreo anticipado

Sumador de 64 bits con acarreo anticipado

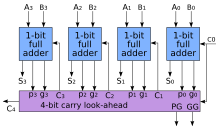
Para reducir el tiempo de cálculo, Weinberger y Smith inventaron una forma más rápida de sumar dos números binarios utilizando sumadores de acarreo anticipado (CLA). ^[8] Introdujeron dos señales ( y ) para cada posición de bit, en función de si un acarreo se propaga desde una posición de bit menos significativa (al menos una entrada es un 1), se genera en esa posición de bit (ambas entradas son 1) o se elimina en esa posición de bit (ambas entradas son 0). En la mayoría de los casos, es simplemente la salida de suma de un medio sumador y es la salida de acarreo del mismo sumador. Después de que se generan y , se crean los acarreos para cada posición de bit. ${\displaystyle P}$ ${\displaystyle G}$ ${\displaystyle P}$ ${\displaystyle G}$ ${\displaystyle P}$ ${\displaystyle G}$

Las derivaciones simples de la recurrencia CLA de Weinberger-Smith son: el sumador de Brent-Kung (BKA), ^[9] y el sumador de Kogge-Stone (KSA). ^{[10] [11]} Esto se demostró en el artículo de Oklobdzija y Zeydel en el IEEE Journal of Solid-State Circutis. ^[12]

Algunas otras arquitecturas de sumadores multibit dividen el sumador en bloques. Es posible variar la longitud de estos bloques en función del retardo de propagación de los circuitos para optimizar el tiempo de cálculo. Estos sumadores basados ​​en bloques incluyen el sumador de acarreo-salto (o acarreo-bypass) que determinará los valores para cada bloque en lugar de cada bit, y el sumador de acarreo-selección que genera previamente la suma y los valores de acarreo para cualquier posible entrada de acarreo (0 o 1) al bloque, utilizando multiplexores para seleccionar el resultado apropiado cuando se conoce el bit de acarreo. ${\displaystyle P}$ ${\displaystyle G}$

Al combinar varios sumadores con acarreo anticipado, se pueden crear sumadores aún más grandes. Esto se puede utilizar en varios niveles para crear sumadores aún más grandes. Por ejemplo, el siguiente sumador es un sumador de 64 bits que utiliza cuatro CLA de 16 bits con dos niveles de unidades de acarreo anticipado .

Otros diseños de sumadores incluyen el sumador de acarreo-selección , el sumador de suma condicional , el sumador de acarreo-salto y el sumador de acarreo-completo.

Sumadores de ahorro de transporte

Si un circuito sumador debe calcular la suma de tres o más números, puede resultar ventajoso no propagar el resultado del acarreo. En su lugar, se utilizan sumadores de tres entradas, que generan dos resultados: una suma y un acarreo. La suma y el acarreo se pueden introducir en dos entradas del sumador de tres números subsiguiente sin tener que esperar a que se propague una señal de acarreo. Sin embargo, después de todas las etapas de la suma, se debe utilizar un sumador convencional (como el de acarreo por ondulación o el de anticipación) para combinar los resultados finales de la suma y el acarreo.

Compresores 3:2

Un sumador completo puede considerarse como un compresor con pérdida 3:2 : suma tres entradas de un bit y devuelve el resultado como un único número de dos bits; es decir, asigna 8 valores de entrada a 4 valores de salida. (el término "compresor" en lugar de "contador" se introdujo en ^[13] ) Por lo tanto, por ejemplo, una entrada binaria de 101 da como resultado una salida de 1 + 0 + 1 = 10 (número decimal 2). El acarreo representa el bit uno del resultado, mientras que la suma representa el bit cero. Del mismo modo, un medio sumador se puede utilizar como un compresor con pérdida 2:2 , comprimiendo cuatro posibles entradas en tres posibles salidas.

Estos compresores se pueden utilizar para acelerar la suma de tres o más sumandos. Si el número de sumandos es exactamente tres, el diseño se conoce como sumador de acarreo-ahorro . Si el número de sumandos es cuatro o más, se necesita más de una capa de compresores, y hay varios diseños posibles para el circuito: los más comunes son los árboles de Dadda y Wallace . Este tipo de circuito se utiliza sobre todo en circuitos multiplicadores , por lo que estos circuitos también se conocen como multiplicadores de Dadda y Wallace.

Sumadores cuánticos

Sumador cuántico completo, que utiliza puertas Toffoli y CNOT . La puerta CNOT que está rodeada por un cuadrado punteado en esta imagen se puede omitir si no se requiere realizar cálculos para restaurar la salida B.

Usando solo las puertas lógicas cuánticas Toffoli y CNOT , es posible producir sumadores completos y medios sumadores cuánticos. ^{[14] [15] [16]} Los mismos circuitos también se pueden implementar en computación reversible clásica, ya que tanto CNOT como Toffoli también son puertas lógicas clásicas .

Dado que la transformada cuántica de Fourier tiene una baja complejidad de circuito , también se puede utilizar de manera eficiente para sumar números. ^{[17] [18] [19]}

Sumadores analógicos

Al igual que en los sumadores binarios, la combinación de dos corrientes de entrada permite sumarlas. Dentro de las limitaciones del hardware, las señales no binarias (es decir, con una base mayor que 2) se pueden sumar para calcular una suma. Esta técnica, también conocida como "amplificador sumador", ^[20] se puede utilizar para reducir la cantidad de transistores en un circuito de suma.

Véase también

• Multiplicador binario
• Sustractor
• Mezclador electrónico : para agregar señales analógicas

Referencias

1. Singh, Ajay Kumar (2010). Diseño de VLSI digital. Prentice Hall India. pág. 321. ISBN 9788120341876– a través de Google Books.
2. Lancaster, Geoffrey A. (2004). Diseño y desarrollo de software Excel HSC. Pascal Press. pág. 180. ISBN 978-1-74125175-3.
3. Mano, M. Morris (1979). Lógica digital y diseño de computadoras . Prentice-Hall . Págs. 119-123. ISBN. 978-0-13-214510-7.
4. Teja, Ravi (15 de abril de 2021), Circuitos de medio sumador y sumador completo , consultado el 27 de julio de 2021
5. Fischer, P. "Einfache Schaltungsblöcke" (PDF) . Universidad de Heidelberg. Archivado desde el original (PDF) el 5 de septiembre de 2021 . Consultado el 5 de septiembre de 2021 .
6. Satpathy, Pinaki (2016). Diseño e implementación de un sumador de selección de acarreo utilizando T-Spice. Anchor Academic Publishing. pág. 22. ISBN 978-3-96067058-2.
7. Burgess, Neil (2011). Sumadores rápidos de acarreo de ondulación en CMOS VLSI de celda estándar. 20.º Simposio IEEE sobre aritmética informática . págs. 103-111.
8. Weinberger y JL Smith, “Una lógica para la adición de alta velocidad”, Oficina Nacional de Normas, Circ. 591, pág. 3-12, 1958.
9. Brent, Richard Peirce ; Kung, Hsiang Te (marzo de 1982). "Un diseño regular para sumadores paralelos". IEEE Transactions on Computers . C-31 (3): 260–264. doi :10.1109/TC.1982.1675982. ISSN  0018-9340. S2CID  17348212. Archivado desde el original el 24 de septiembre de 2017.
10. Kogge, Peter Michael ; Stone, Harold S. (agosto de 1973). "Un algoritmo paralelo para la solución eficiente de una clase general de ecuaciones de recurrencia". IEEE Transactions on Computers . C-22 (8): 786–793. doi :10.1109/TC.1973.5009159. S2CID  206619926.
11. Reynders, Nele; Dehaene, Wim (2015). Diseño de circuitos digitales energéticamente eficientes a voltaje ultrabajo . Circuitos analógicos y procesamiento de señales (1.ª ed.). Cham, Suiza: Springer International Publishing AG Suiza . doi :10.1007/978-3-319-16136-5. ISBN . 978-3-319-16135-8. ISSN  1872-082X. LCCN  2015935431.
12. BR Zeydel, D. Baran, VG Oklobdzija, "Diseño energéticamente eficiente de sumadores VLSI de alto rendimiento", IEEE Journal of Solid-State Circuits, vol. 45, número 6. junio de 2010.
13. VG Oklobdzija y D. Villeger, "Mejora del diseño del multiplicador mediante el uso de un árbol de compresión de columnas mejorado y un sumador final optimizado en tecnología CMOS", IEEE Transactions on VLSI Systems, vol. 3, n.º 2, junio de 1995, 10 páginas.
14. Feynman, Richard P. (1986). "Computadoras mecánicas cuánticas". Fundamentos de la física . 16 (6). Springer Science and Business Media LLC: 507–531. Bibcode :1986FoPh...16..507F. doi :10.1007/bf01886518. ISSN  0015-9018. S2CID  122076550.
15. "Ejemplo de código: sumador completo cuántico". QuTech (Universidad Tecnológica de Delft (TU Delft) y Organización Holandesa para la Investigación Científica Aplicada (TNO)).
16. Dibyendu Chatterjee, Arijit Roy (2015). "Un esquema de semisumador cuántico basado en transmon". Progreso de la física teórica y experimental . 2015 (9): 093A02. Código Bibliográfico :2015PTEP.2015i3A02C. doi : 10.1093/ptep/ptv122 .
17. Draper, Thomas G. (7 de agosto de 2000). "Adición en una computadora cuántica". arXiv : quant-ph/0008033 .
18. Ruiz-Pérez, Lidia; Juan Carlos, García-Escartín (2 de mayo de 2017). "Aritmética cuántica con la transformada cuántica de Fourier". Procesamiento de información cuántica . 16 (6): 152. arXiv : 1411.5949v2 . Código Bibliográfico :2017QuIP...16..152R. doi :10.1007/s11128-017-1603-1. S2CID  10948948.
19. Şahin, Engin (2020). "Operaciones aritméticas cuánticas basadas en la transformada cuántica de Fourier sobre números enteros con signo". Revista Internacional de Información Cuántica . 18 (6): 2050035. arXiv : 2005.00443v3 . Código Bibliográfico :2020IJQI...1850035S. doi :10.1142/s0219749920500355. ISSN  1793-6918.
20. "El amplificador sumador es un sumador de voltaje del amplificador operacional". 22 de agosto de 2013.

Lectura adicional

• Liu, Tso-Kai; Hohulin, Keith R.; Shiau, Lih-Er; Muroga, Saburo (enero de 1974). "Sumadores completos óptimos de un bit con diferentes tipos de puertas". IEEE Transactions on Computers . C-23 (1). Bell Laboratories: IEEE : 63–70. doi :10.1109/TC.1974.223778. ISSN  0018-9340. S2CID  7746693.
• Lai, Hung Chi; Muroga, Saburo (septiembre de 1979). "Sumadores paralelos binarios mínimos con puertas NOR (NAND)". IEEE Transactions on Computers . C-28 (9). IEEE : 648–659. doi :10.1109/TC.1979.1675433. S2CID  23026844.
• Mead, Carver; Conway, Lynn (1980) [diciembre de 1979]. Introducción a los sistemas VLSI (1.ª ed.). Reading, MA, EE. UU.: Addison-Wesley . Código Bibliográfico :1980aw...book.....M. ISBN 978-0-20104358-7. Recuperado el 12 de mayo de 2018 .
• Davio, Marc; Dechamps, Jean-Pierre; Thayse, André (1983). Sistemas digitales, con implementación de algoritmos (1.ª ed.). Philips Research Laboratory , Bruselas, Bélgica: John Wiley & Sons , una publicación de Wiley-Interscience. ISBN 978-0-471-10413-1. Número de serie LCCN  82-2710.
• Gosling, John (enero de 1971). "Revisión de técnicas de adición de alta velocidad". Proc. IEE . 188 (1): 29–35. doi :10.1049/piee.1971.0004.

Enlaces externos

• Medios relacionados con Sumadores (circuitos digitales) en Wikimedia Commons
• Sumador y restador completo de 8 bits, una demostración de un sumador completo interactivo creado en JavaScript únicamente con fines de aprendizaje.
• Demostraciones interactivas de sumadores completos y medios en HTML5
• Shirriff, Ken (noviembre de 2020). "Ingeniería inversa del circuito carry-lookahead en el procesador Intel 8008".